Algorithms Data Structures M 2 Algorithms and Complexity

Algorithms & Data Structures (M) 2 Algorithms and Complexity § Principles § Efficiency analysis § Complexity analysis § O-notation § Recursive algorithms © 2008 David A Watt, University of Glasgow

Principles (1) § An algorithm is a step-by-step procedure for solving a stated problem. § The algorithm will be performed by a processor. – The processor may be human, mechanical, or electronic. § The algorithm must be expressed in steps that the processor is capable of performing. § The algorithm must eventually terminate. – Otherwise it will never yield an answer. 2 -2

Principles (2) § The algorithm must be expressed in some language that the processor “understands”. (But the underlying algorithm is independent of the particular language chosen. ) § The stated problem must be solvable, i. e. , capable of solution by a step-by-step procedure. § Some interesting problems are unsolvable. E. g. : – Can we devise an algorithm to determine whether a given program will terminate or not? – No such algorithm exists, even if the program’s input data are also given! (This is Turing’s famous “halting problem”. ) 2 -3

Remedial maths: logarithms (1) § Consider a positive number y. Then the logarithm of y to the base 2 (written log 2 y) is the number of copies of 2 that must be multiplied together to equal y. § If y is a power of 2, log 2 y is an integer: E. g. : log 2 1 log 2 2 log 2 4 log 2 8 = = 0 1 2 3 since 20 = 1 since 21 = 2 since 22 = 2 2 = 4 since 23 = 2 2 2 = 8 § If y is not a power of 2, log 2 y is a real number: E. g. : log 2 5 2. 32 log 2 7 2. 81 2 -4

Remedial maths: logarithms (2) § log 2 (2 n) = n § log 2 (x y) = log 2 x + log 2 y no. of 2 s multiplied to make x y § log 2 (x/y) = log 2 x – log 2 y 2 -5

Example: logarithms (1) § How many times must we halve the value of n (discarding any remainders) to reach 1? § Suppose that n is a power of 2: E. g. : 8 4 2 1 (8 must be halved 3 times) 16 8 4 2 1 (16 must be halved 4 times) If n = 2 k, n must be halved k times. § Suppose that n is not a power of 2: E. g. : 9 4 2 1 15 7 3 1 (9 must be halved 3 times) (15 must be halved 3 times) If 2 k < n < 2 k+1, n must be halved k times. 2 -6

Example: logarithms (2) § In general, n must be halved k times if: 2 k n < 2 k+1 i. e. , log 2(2 k) log 2 n < log 2(2 k+1) i. e. , k log 2 n < k+1 i. e. , k = floor(log 2 n) taking logs on all sides applying log 2(2 n) = n floor(x) is the largest integer not greater than x § Conclusion: n must be halved floor(log 2 n) times to reach 1. § Corollary: n must be halved floor(log 2 n)+1 times to reach 0. 2 -7

Efficiency analysis § Given a choice of algorithms to solve the same problem, which algorithm is “best”? § Given a particular algorithm: – How much time does it require? – How much space (memory) does it require? – Is it feasible to use it at all? In other words, is it efficient enough to be usable in practice? § In general, both time and space requirements depend on the algorithm’s input data (usually the size of the input data). 2 -8

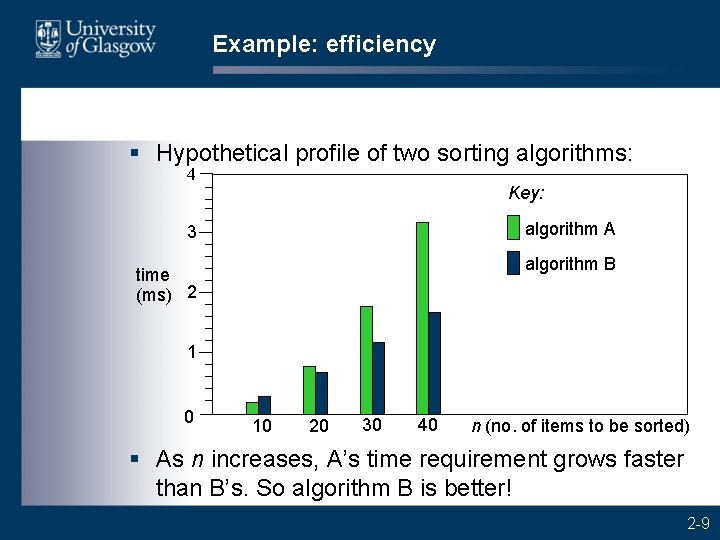
Example: efficiency § Hypothetical profile of two sorting algorithms: 4 Key: algorithm A 3 algorithm B time (ms) 2 1 0 10 20 30 40 n (no. of items to be sorted) § As n increases, A’s time requirement grows faster than B’s. So algorithm B is better! 2 -9

How should we measure time? § Measure time in seconds? + useful in practice – dependent on programming language, compiler, processor speed. § Count algorithm steps? + not dependent on compiler or processor speed – dependent on the way the algorithm is expressed (few “big” steps vs many “small” steps). e. g. , arithmetic § Count characteristic operations? + dependent only on the algorithm itself ops in numerical algorithms, or comparisons in search algorithms + good measure of the algorithm’s intrinsic efficiency. 2 -10

Example: simple power algorithm (1) § Simple power algorithm: To compute bn: 1. Set p to 1. 2. For i = 1, …, n, repeat: 2. 1. Multiply p by b. 3. Terminate yielding p. 2 -11

Example: simple power algorithm (2) § Analysis (counting multiplications): Step 2. 1 performs 1 multiplication. This step is repeated n times. No. of multiplications = n 2 -12

Approximate efficiency analysis § For many interesting algorithms, the exact number of operations is too difficult to analyse mathematically. § We can simplify the analysis by keeping the fastest-growing term but neglecting all slowergrowing terms. 2 -13

Example: smart power algorithm (1) § Idea: b 1000 = b 500. If we know b 500, we can compute b 1000 with only 1 more multiplication! § Smart power algorithm: To compute bn: 1. Set p to 1, set q to b, and set m to n. 2. While m > 0, repeat: 2. 1. If m is odd, multiply p by q. 2. 2. Halve m (discarding any remainder). 2. 3. Multiply q by itself. 3. Terminate yielding p. 2 -14

Example: smart power algorithm (2) § Analysis (counting multiplications): Steps 2. 1– 2. 3 together perform at most 2 multiplications. These steps are repeated as often as we must halve the value of n (discarding any remainder) until it reaches 0, i. e. , floor(log 2 n) + 1 times. Max. no. of multiplications = 2(floor(log 2 n) + 1) = 2 floor(log 2 n) + 2 neglecting +2 (a non-growing term) 2 floor(log 2 n) neglecting floor() 2 log 2 n (which subtracts a small non-growing fraction) 2 -15

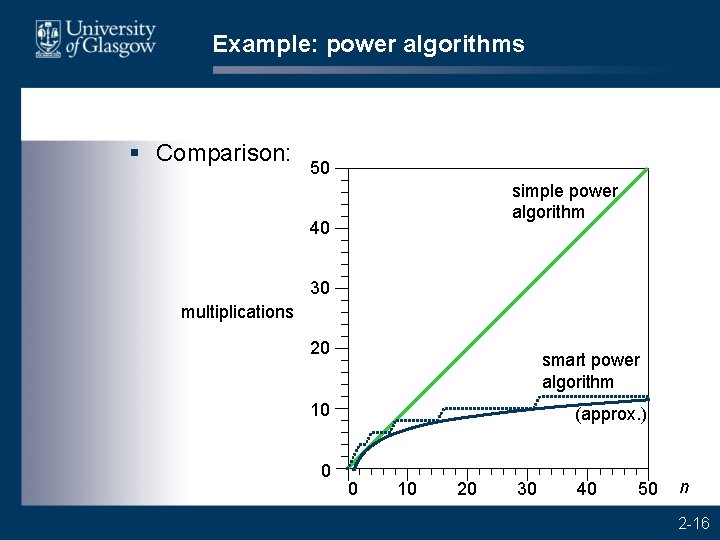
Example: power algorithms § Comparison: 50 simple power algorithm 40 30 multiplications 20 smart power algorithm 10 0 (approx. ) 0 10 20 30 40 50 n 2 -16

Complexity analysis § We can further simplify the analysis, by neglecting the constant factor in the fastestgrowing term. § The resulting formula is the algorithm’s time complexity. It focuses on the growth rate of the algorithm’s time requirement. 2 -17

Example: power algorithms complexity (1) § Analysis of simple power algorithm (counting multiplications): No. of multiplications = n Time required n tmult which is proportional to n. where tmult is the time per multiplication (a constant) Time complexity is of order n. This is written O(n). 2 -18

Example: power algorithms complexity (2) § Analysis of smart power algorithm (counting multiplications): Max. no. of multiplications 2 log 2 n Time required 2 tmult log 2 n which is proportional to log 2 n. Time complexity is of order log 2 n. This is written O(log n). 2 -19

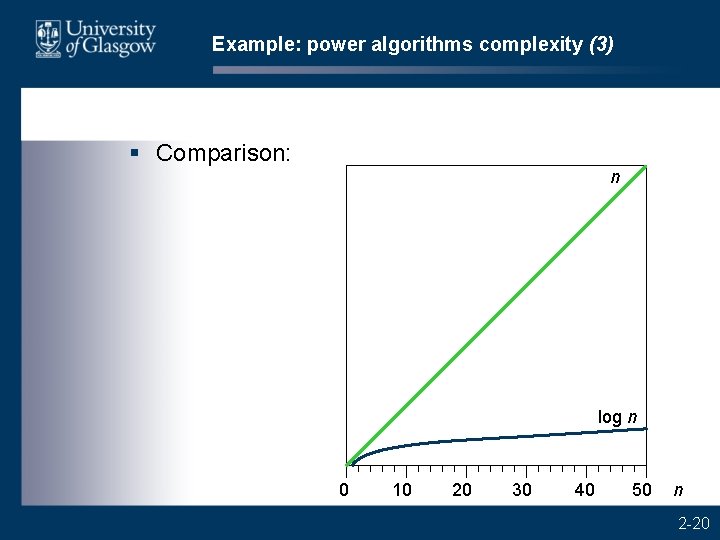
Example: power algorithms complexity (3) § Comparison: n log n 0 10 20 30 40 50 n 2 -20

O-notation (1) § We have seen that O(log n) signifies a slower growth rate than O(n). So an O(log n) algorithm is inherently better than an O(n) algorithm – at least for large values of n. § Complexity O(X) means “of order X”, i. e. , growing proportionally to X. Here X signifies the growth rate, neglecting slower-growing terms and constant factors. 2 -21

O-notation (2) § Common time complexities: O(1) constant time (feasible) O(log n) logarithmic time (feasible) O(n) linear time (feasible) O(n log n) log linear time (feasible) O(n 2) quadratic time (often feasible) O(n 3) cubic time (less often feasible) O(2 n) exponential time (rarely feasible) 2 -22

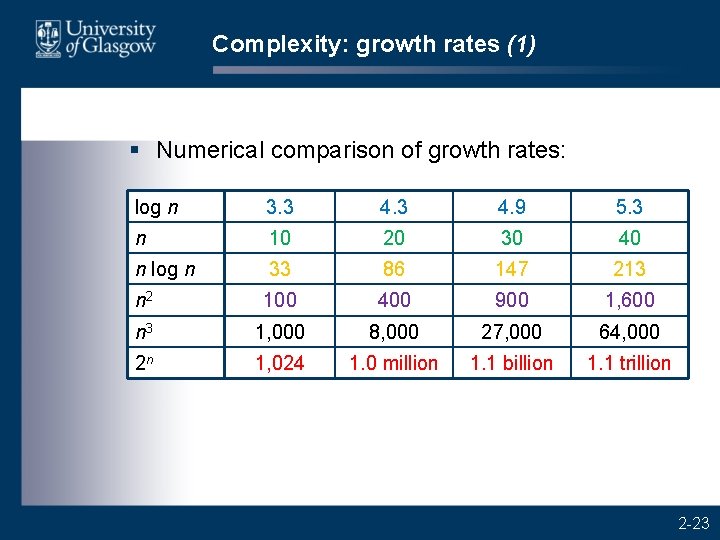
Complexity: growth rates (1) § Numerical comparison of growth rates: log n 3. 3 4. 9 5. 3 n 10 20 30 40 n log n 33 86 147 213 n 2 100 400 900 1, 600 n 3 1, 000 8, 000 27, 000 64, 000 2 n 1, 024 1. 0 million 1. 1 billion 1. 1 trillion 2 -23

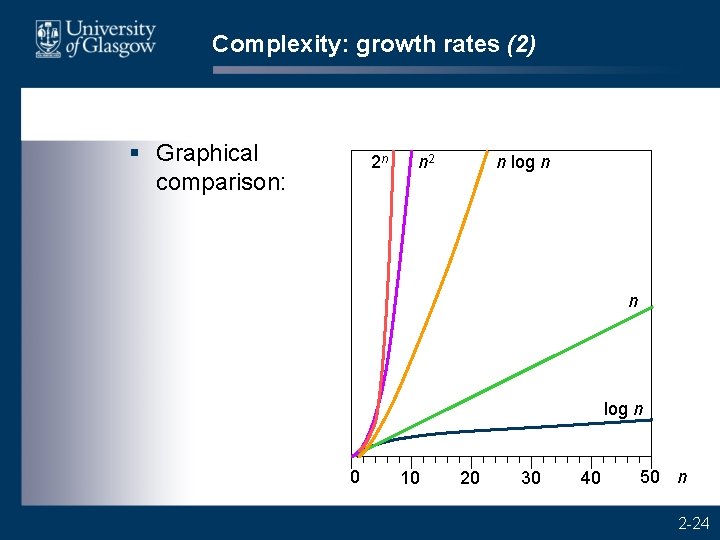
Complexity: growth rates (2) § Graphical comparison: 2 n n 2 n log n 0 10 20 30 40 50 n 2 -24

Recursive algorithms § A recursive algorithm is an algorithm in which at least one step is a “call” to itself. § Sometimes a problem can be solved either by an iterative algorithm or by a recursive algorithm. The recursive version tends to be: + more elegant and easier to understand – less efficient (extra calls consume time and space). § Sometimes a problem can be solved only by a recursive algorithm. 2 -25

When does recursion work? § Given a recursive algorithm, how can we sure that it terminates? § The algorithm must have: – at least one “easy” case – at least one “hard” case. § In an “easy” case, the algorithm must terminate without calling itself. § In a “hard” case, the algorithm may call itself, but only to deal with an “easier” case. 2 -26

Example: rendering integers (1) § Rendering a value means computing a string representation of the value (suitable for printing or display). § Problem: Render a given integer i to the base r (where r is in the range 2… 10). E. g. : i = +29 r=2 rendering = “ 11101” i = +29 r=8 rendering = “ 35” i = +29 r = 10 rendering = “ 29” i = – 29 r=8 rendering = “– 35” 2 -27

Example: rendering integers (2) § Recursive integer rendering algorithm: To render the integer i to the base r: 1. If i < 0: 1. 1. Render the character ‘–’. 1. 2. Render (–i) to the base r. 2. Else, if 0 i < r: 2. 1. Let d be the digit corresponding to i. 2. 2. Render the digit d. 3. Else, if i ≥ r: 3. 1. Let d be the digit corresponding to (i modulo r). 3. 2. Render (i/r) to the base r. 3. 3. Render the digit d. 4. Terminate. hard case: solved by rendering (–i), which is positive easy case: solved directly hard case: solved by rendering (i/r), which has one fewer digit than i 2 -28

Example: rendering integers (3) § Possible implementation in Java: static String render (int i, int r) { // Render i to the base r, where r is in the range 2… 10. String s = ""; if (i < 0) { s += '-'; s += render(-i, r); } else if (i < r) { char d = (char)('0' + i); s += d; } else { char d = (char)('0' + i%r); s += render(i/r, r); s += d; } return s; } 2 -29

Example: Towers of Hanoi (1) § Three vertical poles (1, 2, 3) are mounted on a platform. § A number of discs are provided, all with different diameters. Each disc has a hole in its centre. § All discs are initially threaded on to pole 1, forming a tower with the largest disc at the bottom and the smallest disc at the top. pole 1 pole 2 pole 3 2 -30

Example: Towers of Hanoi (2) § Rules: – One disc may be moved at a time, from the top of one pole to the top of another pole. – A larger disc may not be moved on top of a smaller disc. § Problem: Move the tower of discs from pole 1 to pole 2. 2 -31

Example: Towers of Hanoi (3) § Animation (with 2 discs): pole 1 pole 2 pole 3 2 -32

Example: Towers of Hanoi (4) § Towers of Hanoi algorithm: To move a tower of n discs from pole source to pole dest: 1. If n = 1: 1. 1. Move a single disc from source to dest. 2. Else, if n > 1: 2. 1. Let spare be the remaining pole, other than source and dest. 2. 2. Move a tower of (n– 1) discs from source to spare. 2. 3. Move a single disc from source to dest. 2. 4. Move a tower of (n– 1) discs from spare to dest. 3. Terminate. 2 -33

Example: Towers of Hanoi (5) § Animation (with 6 discs): 1. If n = 1: 1. 1. Move a single disc from source to dest. 2. If n > 1: 2. 1. Let spare be the remaining pole, other than source and dest. 2. 2. Move a tower of (n– 1) discs from source to spare. 2. 3. Move a single disc from source to dest. 2. 4. Move a tower of (n– 1) discs from spare to dest. 3. Terminate. source dest spare 2 -34

Example: Towers of Hanoi (6) § Analysis (counting moves): Let the total no. of moves required to move a tower of n discs be moves(n). Then: moves(n) = 1 + 2 moves(n– 1) if n = 1 if n > 1 Solution: moves(n) = 2 n – 1 Time complexity is O(2 n). 2 -35