Advanced Algorithms Piyush Kumar Lecture 5 Preflow Push

Advanced Algorithms Piyush Kumar (Lecture 5: Preflow Push) Welcome to COT 5405

Today • Preflow Push

Review: Augmenting Path • Maintains a flow in each iteration • Finds a path in the residual graph • Saturates the path to make progress.

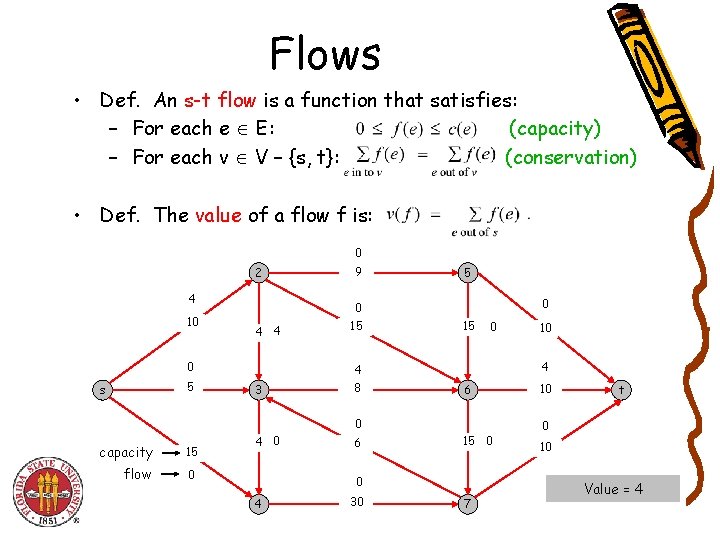
Flows • Def. An s-t flow is a function that satisfies: – For each e E: (capacity) – For each v V – {s, t}: (conservation) • Def. The value of a flow f is: 0 2 4 10 4 4 0 5 s 9 0 15 5 0 15 0 4 4 3 8 6 0 capacity 15 flow 0 4 0 6 15 0 0 4 30 10 7 10 t 0 10 Value = 4

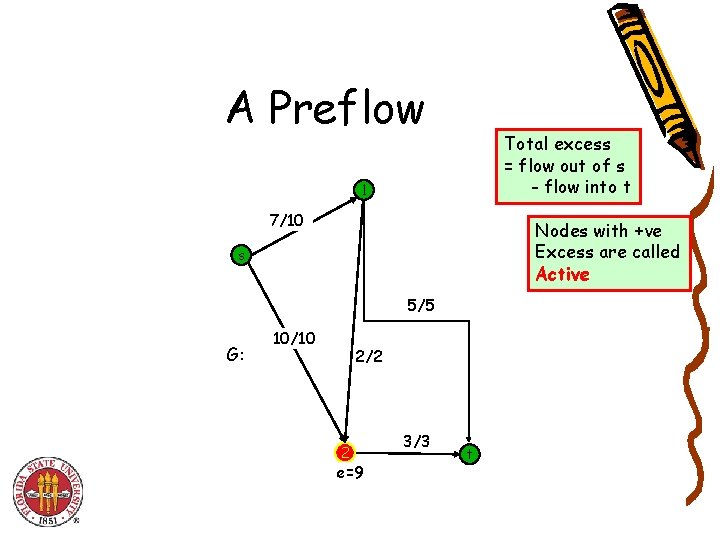
A Preflow • Def. An preflow is a function that satisfies: – For each e E: (capacity) – For each v V – {s, t}: (weak conservation) • Def. The excess of a preflow f at node v : – Required to be non-negative except s, t 1. 2. 3. 4. Algorithm maintains preflow (not flow) Each vertex is associated with a height Flow is “downhill” Vertices with excess are sometimes “lifted/relabeled”.

A Preflow Total excess = flow out of s - flow into t 1 7/10 Nodes with +ve Excess are called Active s 5/5 G: 10/10 2/2 2 e=9 3/3 t

Labelling/Height function • H: V -> N – Source and Sink condition • h(s) = n • h(t) = 0 Invariant – Steepness condition • For all (v, w) in Ef , h(v) <= h(w)+1 • Here Ef is the residual graph. Compatibility of preflows and labellings

Lemma • If s-t preflow f is compatible with the labelling h, then there is no s-t path in the residual graph Gf. • Cor: If s-t flow f is compatible with a labelling h, then f is a flow of maximum value.

Initial Preflow f • • h(v) = 0 for all v <> s h(s) = n f(e) = ce for all e=(s, v) f(e) = 0 for all other edges. The algorithm gradually transforms a preflow to a flow. Why?

Lemma • An s-t preflow f is compatible with a labelling h, then there is no s-t path in the residual graph Gf. • Cor: An s-t flow f is maximum when its compatible with labelling h.

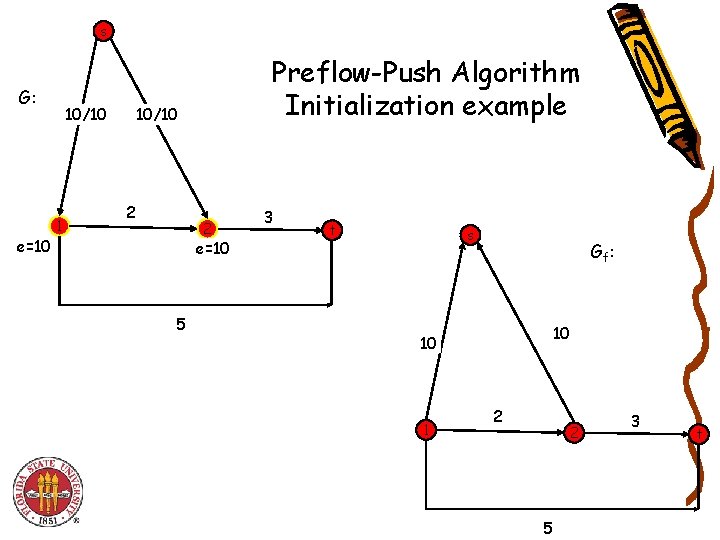
s G: e=10 10/10 1 Preflow-Push Algorithm Initialization example 10/10 2 2 e=10 5 3 t s Gf: 10 10 1 2 2 5 3 t

Basic Operation 1 Push forward edge • Suppose e(u)>0, cf(u, v)>0, (u, v) in Ef (u, v) is a forward edge h[u]= h[v]+1 • Push as much flow across (u, v) as possible r = min (e[u], c(u, v) – f(e)) Increase f(e) by r.

Basic Operation 2 Push backward edge • Suppose e(u)>0, cf(u, v)>0, (u, v) in Ef (u, v) is a backward edge h[u]= h[v]+1 • Push as much flow across (u, v) as possible r = min (e[u], f(e)) Decrease f(e) by r. The preflow push algorithm will try to push from Active nodes towards the sink (maintaining compatibility with the labelling/heights of the nodes)

Basic Operation 3 Lift/Relabel • When no push can be done from overflowing vertex (except s, t) • Suppose e[u]>0, and for all (u, v) in Ef : h[u] £ h[v], u ¹ s, u ¹ t – Set h[u] = h[u] + 1

Preflow-Push • Initialize • While there is a node v <> t with ef(v) > 0 E – If w such that push (f, h, v, w) is possible • Push(f, h, v, w) – Else • Relabel(f, h, v)

Preflow push demo

Invariants 1. The labels are >= 0 and integers 2. f is a preflow, if the capacities are integral, the preflows are integral. 3. The preflow f and labelling h are compatible. 4. The height of a node never decreases.

Lemma • Lef f be a preflow. If excessf(v) > 0 then there is a path in Gf from v to source s. • Pf: Let A denote all the nodes that have a path to s in Gf. B = V A. What happens to edges inside B? If e has only its head in B? If e has only its tail in B? –fout(B)

Lemmas • The height of a node is upper bounded by 2 n-1. • Cor: Each node is relabeled at most 2 n-1 times, hence total relabels is upper bounded by 2 n 2

Lemma: Saturating Pushes • Throughout the algorithm, the number of saturating push operations is at most 2 mn. • Pf: Look at a saturating push along an edge. When can another saturating push happen thru the same edge? (If it needs lifting, how many lifts can one do on such a node in total? )

Potential function arguments • Consider a joint bank account held by A, B, and C • The account starts with an initial deposit of at most n 2. – A only makes withdrawals, each for 1 or more. – B makes fewer than n 2 deposits. Each deposit is for at most 1. – C makes fewer than nm withdrawals and deposits. Each deposit is for at most n. – The account never goes below 0. • What is the maximum number of withdrawals for A?

Lemma: Non-Saturating Pushes Potential Functions Argument • Lemma: The number of non-saturating push operations is bounded by 4 mn 2 • Pf: Define: A non saturating push decreases it by at least 1. A saturating push increases it by at most 2 n-1 A relabel increases it by exactly 1. If we pick the active node at maximum height For pushing, we can get O(n^3) non-sat. pushes.

Modifications • A simple modification gives O(n 3). • Theorem: The total running time of the algorithm is upper bounded by O(mn 2)

References • R. K. Ahuja, T. L. Magnanti, and J. B. Orlin. Network Flows. Prentice Hall, 1993. (Reserved in Dirac) • K. Mehlhorn and S. Naeher. The LEDA Platform for Combinatorial and Geometric Computing. Cambridge University Press, 1999. 1018 pages