Advanced Algorithms Piyush Kumar Lecture 5 Page Rank

Advanced Algorithms Piyush Kumar (Lecture 5: Page. Rank) Welcome to COT 5405

Quick Recap: Linear Algebra Matrices Source: http: //www. phy. cuhk. edu. hk/phytalent/mathphy/

1. 1 Matrices Square matrices §When m = n, i. e. , 3

1. 2 Operations of matrices Sums of matrices Example: if and Evaluate A + B and A – B. 4

1. 2 Operations of matrices Scalar multiplication Example: . Evaluate 3 A. 5

1. 2 Operations of matrices Properties Matrices A, B and C are conformable, §A + B = B + A (commutative law) §A + (B +C) = (A + B) +C (associative law) §l(A + B) = l. A + l. B, where l is a scalar (distributive law) Can you prove them? 6

1. 2 Operations of matrices Matrix multiplication §If A = [aij] is a m p matrix and B = [bij] is a p n matrix, then AB is defined as a m n matrix C = AB, where C= [cij] with for 1 i m, 1 j n. Example: Evaluate c 21. , and C = AB. 7

1. 2 Operations of matrices Matrix multiplication Example: , , Evaluate C = AB. 8

1. 2 Operations of matrices Properties Matrices A, B and C are conformable, §A(B + C) = AB + AC §(A + B)C = AC + BC However §A(BC) = (AB) C §AB BA in general §AB = 0 NOT necessarily imply A = 0 or B = 0 §AB = AC NOT necessarily imply B = C 9

Identity Matrix Examples of identity matrices: and

1. 3 Types of matrices The transpose of a matrix §The matrix obtained by interchanging the rows and columns of a matrix A is called the transpose of A (write AT). Example: The transpose of A is §For a matrix A = [aij], its transpose AT = [bij], where bij = aji. 11

1. 3 Types of matrices The inverse of a matrix §If matrices A and B such that AB = BA = I, then B is called the inverse of A (symbol: A-1); and A is called the inverse of B (symbol: B-1). Example: Show B is the inverse of matrix A. Ans: Note that Can you show the details? 12

1. 3 Types of matrices Symmetric matrix §A matrix A such that AT = A is called symmetric, i. e. , aji = aij for all i and j. §A + AT must be symmetric. Why? Example: is symmetric. §A matrix A such that AT = -A is called skewsymmetric, i. e. , aji = -aij for all i and j. §A - AT must be skew-symmetric. Why? 13

1. 4 Properties of matrix §(AB)-1 = B-1 A-1 §(AT)T = A and (l. A)T = l AT §(A + B)T = AT + BT §(AB)T = BT AT 14

The determinant of a 2 × 2 matrix: n Note: 1. For every square matrix, there is a real number associated with this matrix and called its determinant 2. It is common practice to delete the matrix brackets 3. 15 Source: http: //www. management. ntu. edu. tw/~jywang/course/

Historically, the use of determinants arose from the recognition of special patterns that occur in the solutions of linear systems: n Note: 1. a 11 a 22 - a 21 a 12≠ 0 2. x 1 and x 2 have the same denominator, and this quantity is called the determinant of the coefficient matrix A 3. 16

Ex. 1: (The determinant of a matrix of order 2) n Note: The determinant of a matrix can be positive, zero, or negative 3. 17

1. 5 Determinants The following properties are true for determinants of any order. 1. If every element of a row (column) is zero, e. g. , 2. |AT| = |A| , then |A| = 0. determinant of a matrix = that of its transpose 3. |AB| = |A||B| 18

Eigenvalues and Eigenvectors Ax = λx Should not exist? det(A − λI) = 0. Fact: A and transpose(A) have the same eigenvalues. Why?

Page Ranking

Task of search engines Crawl Build indices so that one can search keywords efficiently. Rate the importance of pages. One example is the simple algorithm named pagerank.

The basic idea Mimic democracy! Use the brains of all people collectively.

The basic idea Mimic democracy! Use the brains of all people collectively for the ranking. What’s wrong with counting backlinks? Should page 1 be ranked above page 4?

Voting using backlinks? But then we don’t want an individual to cast more than one vote? Normalize?

Normalized Voting?

Link Matrix (for the given web):

Link Matrix (for the given web): Most important node = 1?

Definition A square matrix is called column stochastic if all of its entries are non-negative and the entries in each column sum to 1. Lemma: Every column stochastic matrix has 1 as an eigenvalue. Proof: A and A’ = transpose of A, have the same eigenvalues: Why?

Two shortcomings Nonunique Rankings. Dangling nodes : Nodes with no outgoing edges. The matrix is no longer column stochastic. Can we transform it into one easily?

Nonunique Rankings Not clear: Which linear combination should we pick for the ranking?

Nonunique Rankings

Nonunique Rankings

Modification of the Link Matrix The value of m used by google (1998) was. 15 For any m between 0, 1; M is column stochastic. M can be used to compute unambiguous importance scores (in the absence of dangling nodes) For m = 1, the only normalized eigenvector with eigenvalue 1 is ?

Modification of the Link Matrix

Example 1 For our first example graph, m = 0. 15.

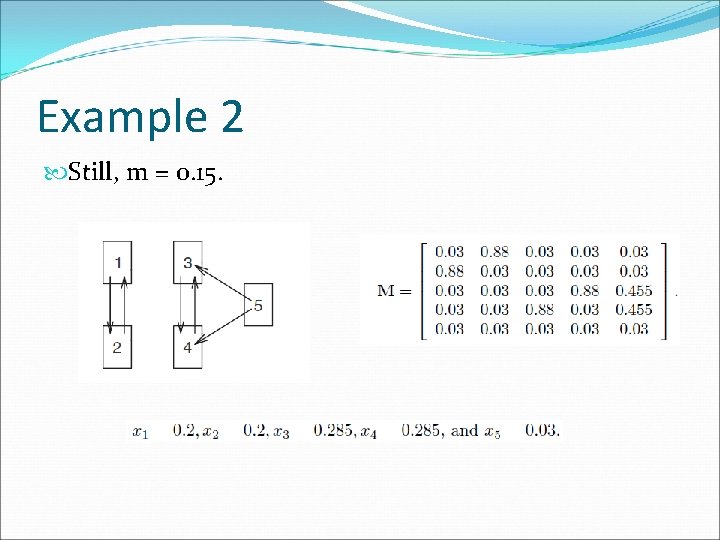
Example 2 Still, m = 0. 15.

Towards the proof Proof by Contradiction? -> Let x be an eigenvector with mixed signs for the eigenvalue 1. For real numbers

Towards the proof

A punchline

The Algorithm (aka Power Method)

c?

One last lemma…

Why does it converge?

The main theorem For figure 2:

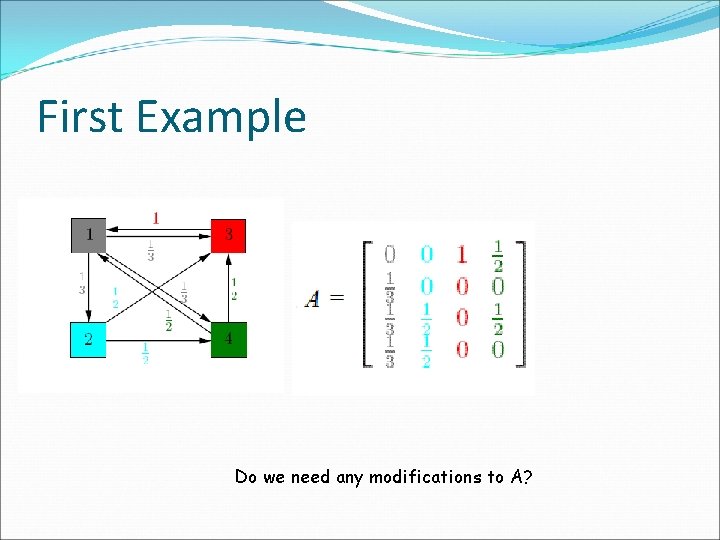
First Example Do we need any modifications to A?

Calculations

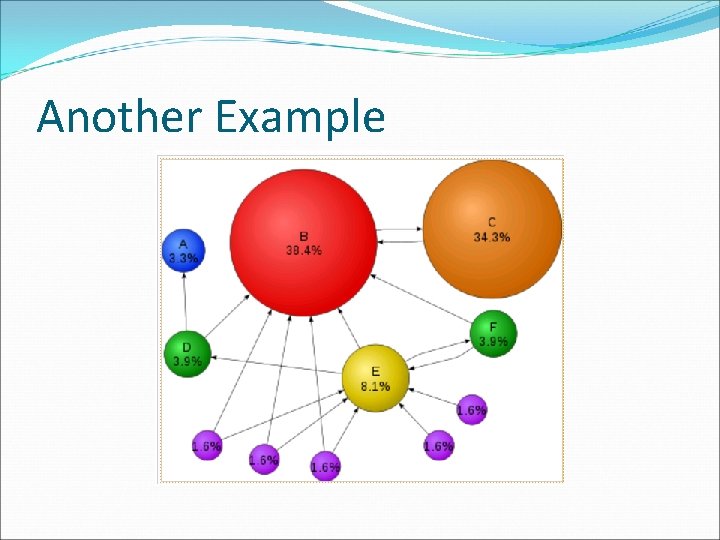
Another Example

Random Surfer Model The 85 -15 Rule: Assume that 85 per cent of the time the random surfer clicks a random link on the current page (each link chosen with equal probability) 15 percent of the time the random surfer goes directly to a random page (all pages on the web chosen with equal probability).

Random Surfer Model Cons No one chooses links or pages with equal probability. There is no real potential to surf directly to each page on the web. The 85 -15 (or any fixed) breakdown is just a guess. Back Button? Bookmarks? Despite these flaws, the model is good enough that we have learnt a great deal about the web using it.

Related stuff to explore Random walks and Markov Chains. Random Graph construction using Random walks. Absorbing Markov Chains. Ranking with not too many similar items at the top. Dynamical Systems point of view. Equilibrium or Stationary Distributions. Rate of convergence. Perron-Frobenius Theorem Intentional Surfer model. Markov Chain Slides: http: //www. math. dartmouth. edu/archive/m 20 x 06/public_html/Lecture 13. pdf http: //www. math. dartmouth. edu/archive/m 20 x 06/public_html/Lecture 14. pdf http: //www. math. dartmouth. edu/archive/m 20 x 06/public_html/Lecture 15. pdf

Homework 1 Implementation: Parse wikipedia pages and find pageranks of top 1000 pages of the given input. (TBA) Theory: Solve Exercises in the given paper. (Online) There are 24 questions in total in the paper (including subproblems marked with a filled disc, Example, problem 6 has 3 subproblems). Pick the first two characters of your fsu. edu email address. Example “pk” for pkumar@fsu. edu. (all lowercase) Represent in hex : “ 706 B” = x = Your hex number goes here. Calculate f 1 = ((x mod 3 D) mod 18)+1 Calculate f 2 = (f 1 + 12) mod 18 Solve those two exercises in the paper. Write the problems you solve (including problem numbers) and the solution in Latex. Submit.