Advanced Algorithms Piyush Kumar Lecture 6 Max Flow

Advanced Algorithms Piyush Kumar (Lecture 6: Max. Flow Min. Cut Applications) Welcome to COT 5405

Announcements • Homework 2 Will be announced soon. • Collect graded homework 1 from me after class.

Today • Complete Preflow Push • Bipartite matching/Hall’s theorem • Application of Max. Flow Min. Cut – Image segmentation – Edge Disjoint paths

Applications Max Flow Min Cut

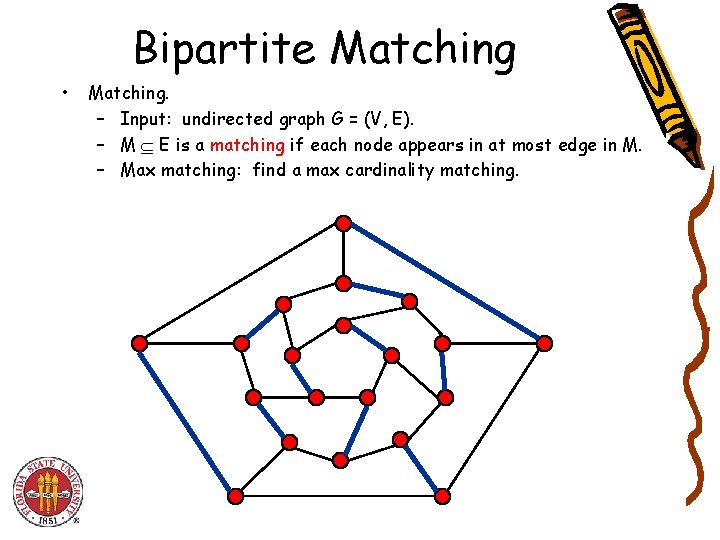
Bipartite Matching • Matching. – Input: undirected graph G = (V, E). – M E is a matching if each node appears in at most edge in M. – Max matching: find a max cardinality matching.

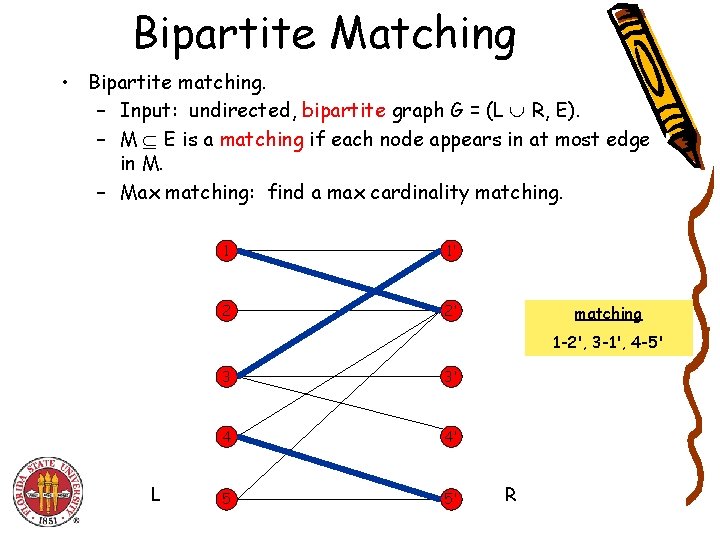
Bipartite Matching • Bipartite matching. – Input: undirected, bipartite graph G = (L R, E). – M E is a matching if each node appears in at most edge in M. – Max matching: find a max cardinality matching. 1 1' 2 2' matching 1 -2', 3 -1', 4 -5' L 3 3' 4 4' 5 5' R

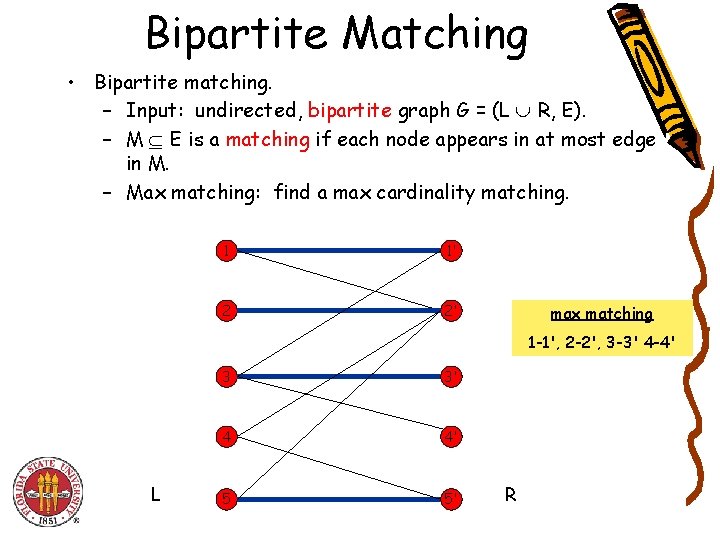
Bipartite Matching • Bipartite matching. – Input: undirected, bipartite graph G = (L R, E). – M E is a matching if each node appears in at most edge in M. – Max matching: find a max cardinality matching. 1 1' 2 2' max matching 1 -1', 2 -2', 3 -3' 4 -4' L 3 3' 4 4' 5 5' R

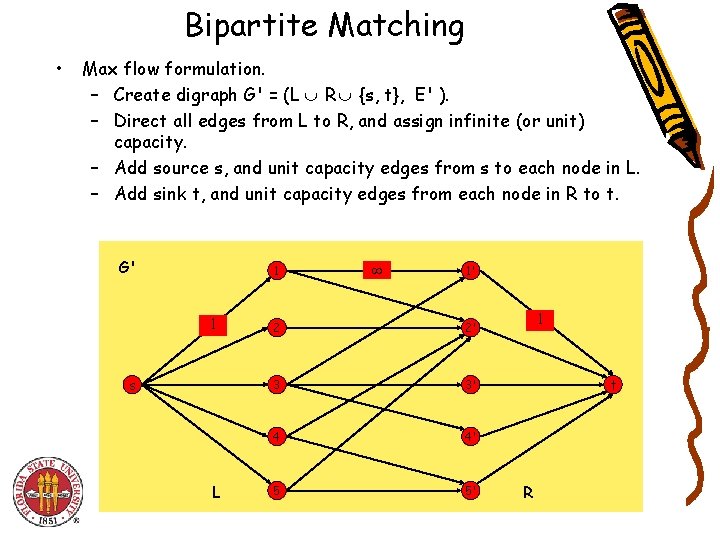
Bipartite Matching • Max flow formulation. – Create digraph G' = (L R {s, t}, E' ). – Direct all edges from L to R, and assign infinite (or unit) capacity. – Add source s, and unit capacity edges from s to each node in L. – Add sink t, and unit capacity edges from each node in R to t. G' 1 1 s L 1' 2 2' 3 3' 4 4' 5 5' 1 t R

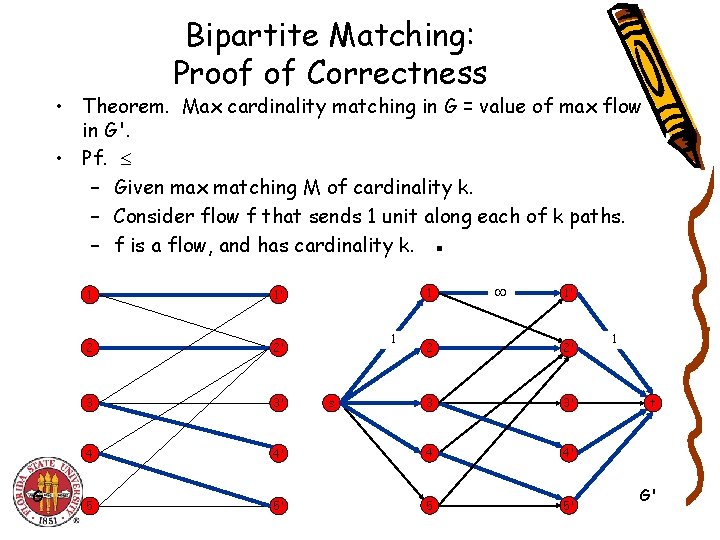
Bipartite Matching: Proof of Correctness • Theorem. Max cardinality matching in G = value of max flow in G'. • Pf. – Given max matching M of cardinality k. – Consider flow f that sends 1 unit along each of k paths. – f is a flow, and has cardinality k. ▪ G 1 1' 2 2' 3 3' 4 5 1 1 1' 2 2' 3 3' 4' 4 4' 5' 5 5' s 1 t G'

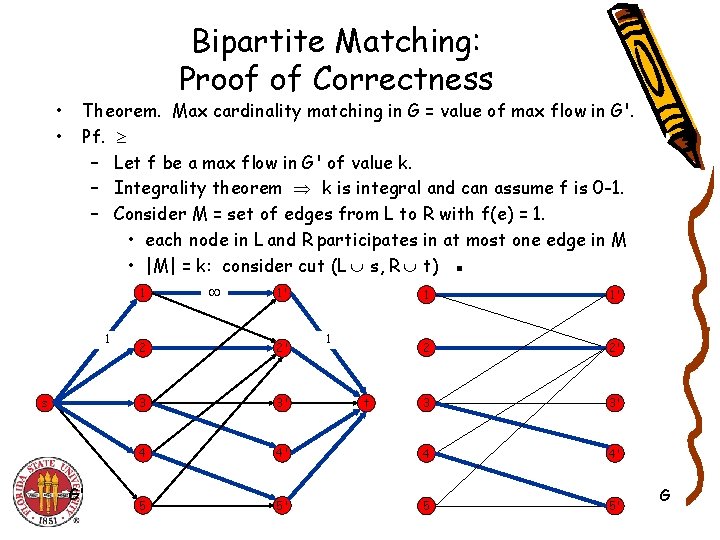
• • Bipartite Matching: Proof of Correctness Theorem. Max cardinality matching in G = value of max flow in G'. Pf. – Let f be a max flow in G' of value k. – Integrality theorem k is integral and can assume f is 0 -1. – Consider M = set of edges from L to R with f(e) = 1. • each node in L and R participates in at most one edge in M • |M| = k: consider cut (L s, R t) ▪ 1 1 s G' 1' 1 1 1' 2 2' 3 3' 4 4' 5 5' t G

Perfect Matching • Def. A matching M E is perfect if each node appears in exactly one edge in M. • Q. When does a bipartite graph have a perfect matching? • Structure of bipartite graphs with perfect matchings. – Clearly we must have |L| = |R|. – What other conditions are necessary? – What conditions are sufficient?

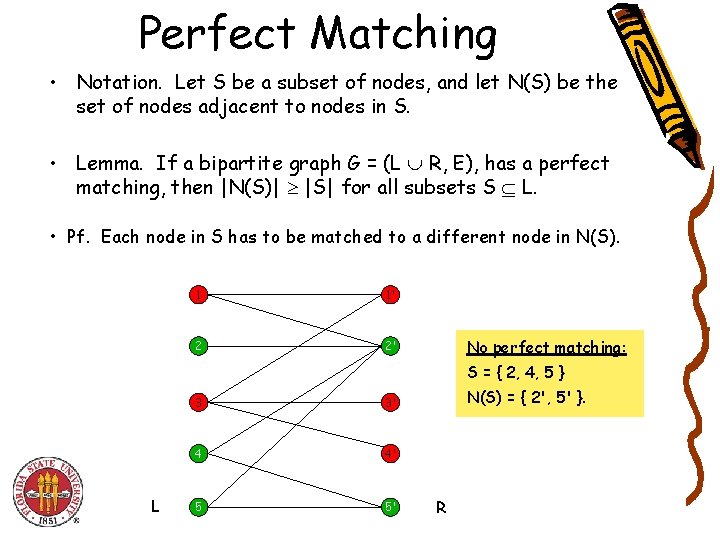
Perfect Matching • Notation. Let S be a subset of nodes, and let N(S) be the set of nodes adjacent to nodes in S. • Lemma. If a bipartite graph G = (L R, E), has a perfect matching, then |N(S)| |S| for all subsets S L. • Pf. Each node in S has to be matched to a different node in N(S). 1 1' 2 2' No perfect matching: S = { 2, 4, 5 } L 3 3' 4 4' 5 5' N(S) = { 2', 5' }. R

Marriage Theorem • Marriage Theorem. [Frobenius 1917, Hall 1935] Let G = (L R, E) be a bipartite graph with |L| = |R|. Then, G has a perfect matching or there is exists S L such that |N(S)| < |S|. Pf: When there is no perfect matching, Use max-flow min-cut theorem on a bipartite graph, to find the cut(A’, B’) < n. Let A = L ∩ A’ Claim 1: N(A) A’ Claim 2: |R ∩ A’| >= N(A) Claim 3: |L ∩ B’ | = n - |A| Claim 4: c(A’, B’) = |L ∩ B’ | + |R ∩ A’| < n

Bipartite Matching: Running Time • Which max flow algorithm to use for bipartite matching? – Generic augmenting path: O(m val(f*) ) = O(mn). – Capacity scaling: O(m 2 log C ) = O(m 2). – Shortest augmenting path: O(m n 1/2). • Non-bipartite matching. – Structure of non-bipartite graphs is more complicated, but well-understood. [Tutte-Berge, Edmonds-Galai] – Blossom algorithm: O(n 4). [Edmonds 1965] – Best known: O(m n 1/2). [Micali-Vazirani 1980]

7. 10 Image Segmentation 15

Image segmentation

Image Segmentation • Image segmentation. – Central problem in image processing. – Divide image into coherent regions. • Ex: To recognize a hand (or face/iris/fingerprint) from the background. (And find out if the person is known to the system)

Image Segmentation • Foreground / background segmentation. – Label each pixel in picture as belonging to foreground or background. – V = set of pixels, E = pairs of neighboring pixels. – ai 0 is likelihood pixel i in foreground. – bi 0 is likelihood pixel i in background. – pij 0 is separation penalty for labeling one of i and j as foreground, and the other as background. • Goals. – Accuracy: if ai > bi in isolation, prefer to label i in foreground. – Smoothness: if many neighbors of i are labeled foreground, we should be inclined to label i as foreground. – Find partition (A, B) that maximizes: foreground background

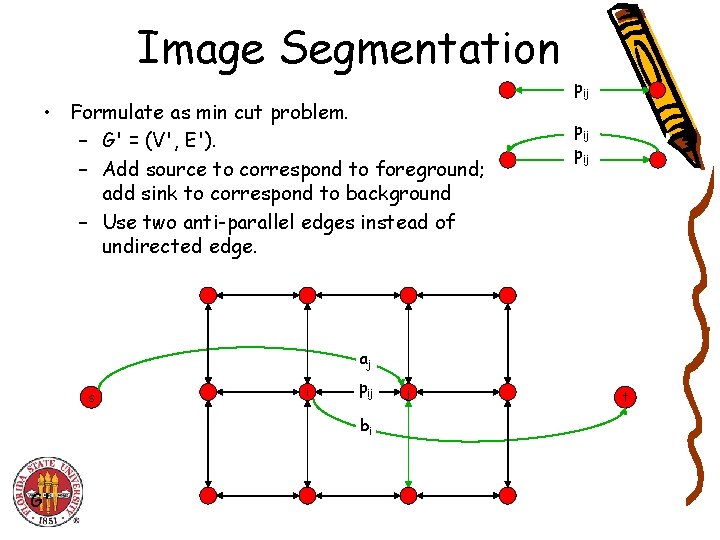
Image Segmentation • Formulate as min cut problem. – Maximization. – No source or sink. – Undirected graph. • Turn into minimization problem. – Maximizing is equivalent to minimizing – or alternatively

Image Segmentation • Formulate as min cut problem. – G' = (V', E'). – Add source to correspond to foreground; add sink to correspond to background – Use two anti-parallel edges instead of undirected edge. pij pij aj s i pij bi G' j t

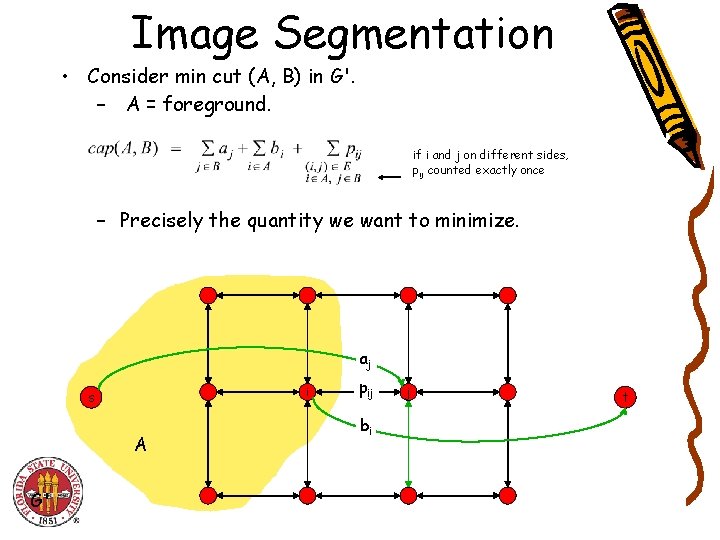
Image Segmentation • Consider min cut (A, B) in G'. – A = foreground. if i and j on different sides, pij counted exactly once – Precisely the quantity we want to minimize. aj i s A G' pij bi j t

Edge Disjoint paths

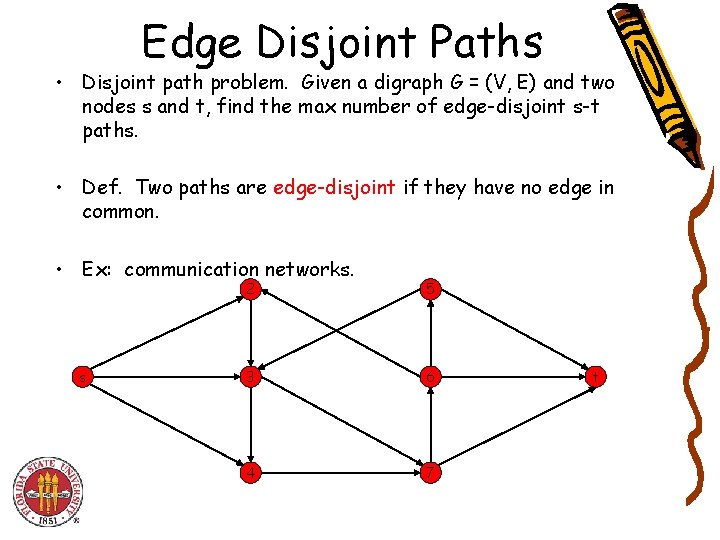
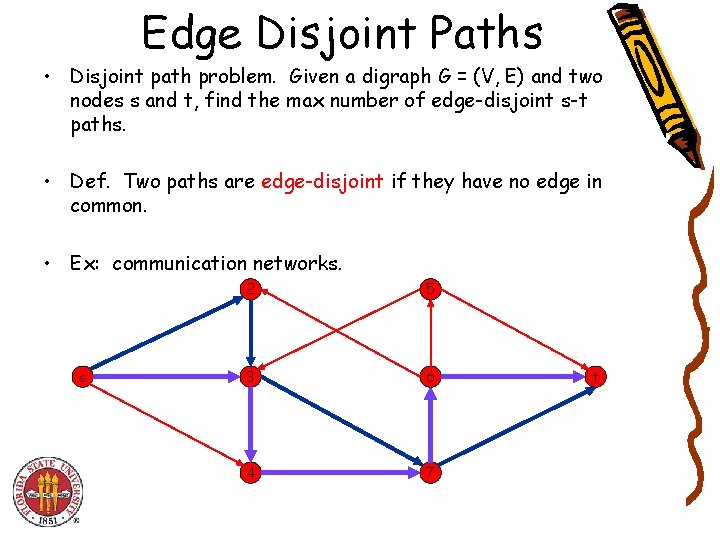
Edge Disjoint Paths • Disjoint path problem. Given a digraph G = (V, E) and two nodes s and t, find the max number of edge-disjoint s-t paths. • Def. Two paths are edge-disjoint if they have no edge in common. • Ex: communication networks. s 2 5 3 6 4 7 t

Edge Disjoint Paths • Disjoint path problem. Given a digraph G = (V, E) and two nodes s and t, find the max number of edge-disjoint s-t paths. • Def. Two paths are edge-disjoint if they have no edge in common. • Ex: communication networks. s 2 5 3 6 4 7 t

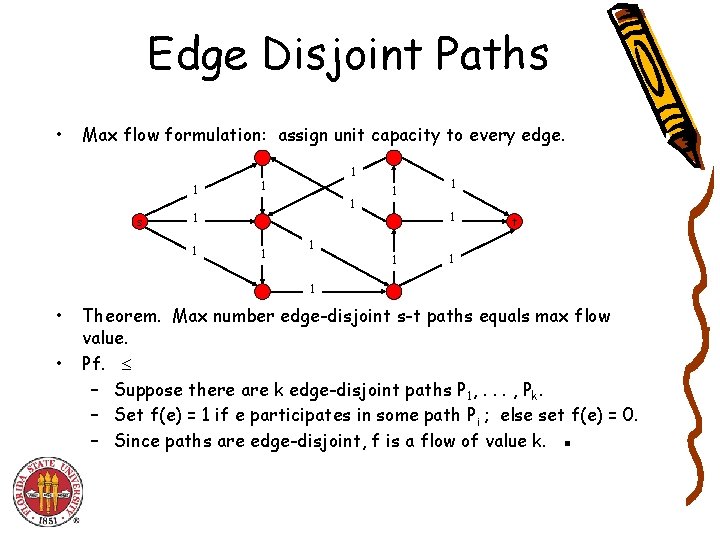
Edge Disjoint Paths • Max flow formulation: assign unit capacity to every edge. 1 s 1 1 1 t 1 1 • • Theorem. Max number edge-disjoint s-t paths equals max flow value. Pf. – Suppose there are k edge-disjoint paths P 1, . . . , Pk. – Set f(e) = 1 if e participates in some path Pi ; else set f(e) = 0. – Since paths are edge-disjoint, f is a flow of value k. ▪

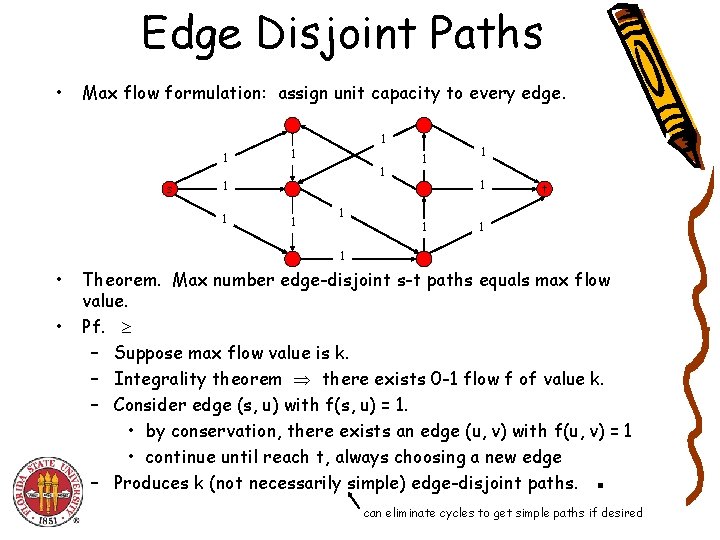
Edge Disjoint Paths • Max flow formulation: assign unit capacity to every edge. 1 s 1 1 1 t 1 1 • • Theorem. Max number edge-disjoint s-t paths equals max flow value. Pf. – Suppose max flow value is k. – Integrality theorem there exists 0 -1 flow f of value k. – Consider edge (s, u) with f(s, u) = 1. • by conservation, there exists an edge (u, v) with f(u, v) = 1 • continue until reach t, always choosing a new edge – Produces k (not necessarily simple) edge-disjoint paths. ▪ can eliminate cycles to get simple paths if desired

Menger’s theorem • In every directed graph with nodes s and t, the maximum number of edge-disjoint s-t paths is equal to the minimum number of edges whose removal separates s from t. • Special case of Max. Flow Min. Cut theorem. • We cud use this theorem instead of the Max. Flow Min. Cut theorem in the proof of Hall’s theorem.

Homework 2 • Read and design power point/latex slides (use beamer) (any one of the following) – – – – Baseball elimination Weighted matching with costs Project selection Airline scheduling Survey design Circulation and demands Advertising policy (Yahoo) Problem : 16 Search cohesive groups : Problem 46.

References • R. K. Ahuja, T. L. Magnanti, and J. B. Orlin. Network Flows. Prentice Hall, 1993. (Reserved in Dirac) • K. Mehlhorn and S. Naeher. The LEDA Platform for Combinatorial and Geometric Computing. Cambridge University Press, 1999. 1018 pages