Linear Programming Max Flow Min Cut Orgad Keller

Linear Programming – Max Flow – Min Cut Orgad Keller

Linear Programming n We have an objective function: n Subject to constraints: Orgad Keller - Algorithms 2 2

Linear Programming n Given all parameters n we want to find the optimal Orgad Keller - Algorithms 2 - 3

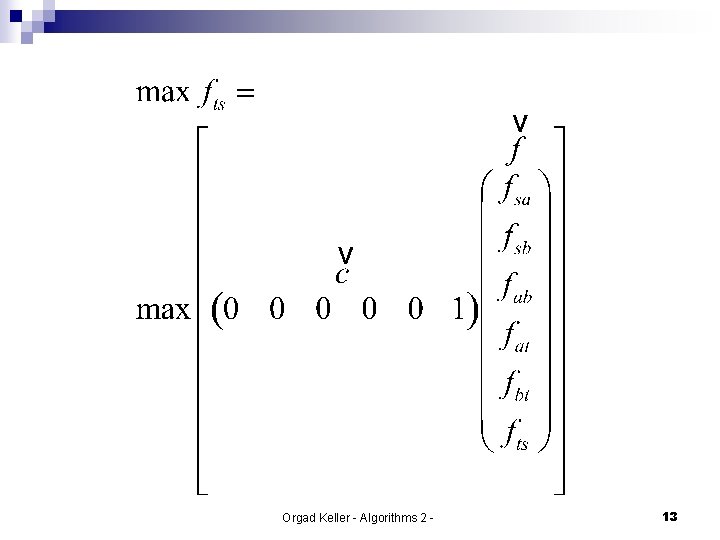
Linear Programming n It is easier to present the problem with a matrix and vectors: Orgad Keller - Algorithms 2 - 4

The Dual Problem n Given the Primal Problem: n It’s Dual Problem is defined as: Orgad Keller - Algorithms 2 - 5

Strong Duality Theorem n Given a problem and it’s dual problem, then: n In other words, the optimal objective function’s value for the primal problem, is equal to the optimal objective function’s value for the dual problem. Orgad Keller - Algorithms 2 - 6

Maximum Flow As you remember from Algorithms I n Given a directed graph , two vertices and a capacity for each edge n We want to find a flow function so that the flow value is maximal n Orgad Keller - Algorithms 2 - 7

Maximum Flow n But, we are subject to some rules: ¨ ¨What ¨ goes in must come out: Capacity restrictions: Orgad Keller - Algorithms 2 - 8

Max Flow with Linear Programming n We’ll show by a simple example: 1 3 2 Orgad Keller - Algorithms 2 - 9

Max Flow with Linear Programming n We want to present the example in the form: ¨ Subject to: Orgad Keller - Algorithms 2 - 10

Max Flow with Linear Programming n Formally: 3 1 1 2 3 But we don’t permit equalities Orgad Keller - Algorithms 2 - 11

Max Flow with Linear Programming ¨ So we’ll add another edge, and change the problem’s representation a little. 3 1 1 3 2 ∞ Orgad Keller - Algorithms 2 - 12

Orgad Keller - Algorithms 2 - 13

Orgad Keller - Algorithms 2 - 14

Minimum Cut As you remember from Algorithms I n Given a directed graph , two vertices and a weight for each edge n We want to find a minimal-weight subset of edges such that if we’ll remove them, we won’t be able to travel from to. n Orgad Keller - Algorithms 2 - 15

Minimum Cut n In other words: ¨ We’ll choose , where: , , such that the cut value, is minimal. Orgad Keller - Algorithms 2 - 16

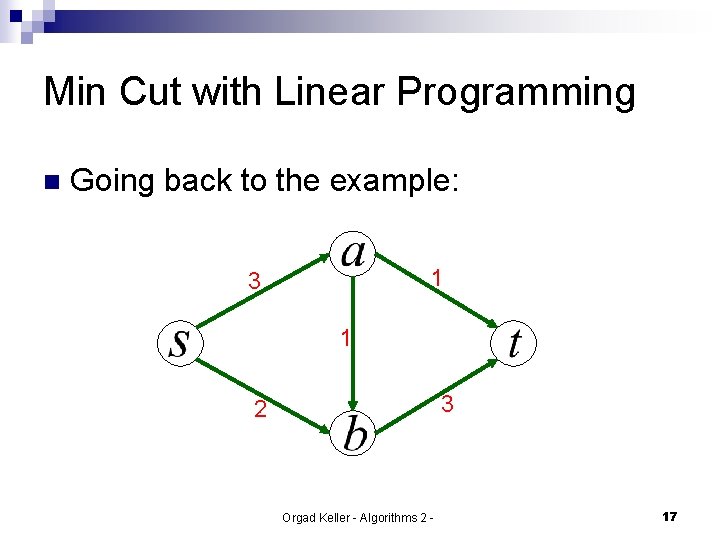
Min Cut with Linear Programming n Going back to the example: 1 3 2 Orgad Keller - Algorithms 2 - 17

Min Cut with Linear Programming 3 n 1 1 What about: 3 2 This look like And we know that ¨ Is that enough? ¨ We haven’t ensured paths from Orgad Keller - Algorithms 2 - to are cut. 18

Min Cut with Linear Programming 3 n Beside a variable for every edge , we’ll want a variable for every vertex such that: Orgad Keller - Algorithms 2 - 1 1 2 3 , 19

Min Cut with Linear Programming 3 n Let’s take ¨ If for instance: is in the cut , that ¨ If is not in the cut that either or ¨ So 1 1 2 3 that means , that means or it is the same to constrain: Orgad Keller - Algorithms 2 - 20

Max Flow with Linear Programming n Formally: 3 1 1 2 3 In order to ensure Orgad Keller - Algorithms 2 - 21

Orgad Keller - Algorithms 2 - 22

Orgad Keller - Algorithms 2 - 23

Orgad Keller - Algorithms 2 - 24

Max Flow – Min Cut Theorem We now see that the problems are dual n So also according to the Strong Duality Theorem, Max Flow = Min Cut n Orgad Keller - Algorithms 2 - 25

Integer Values We want integer values for the variables, but this is LP, not IP! n So how do we know that the solution will yield integer values for the variables? n Theroem: If the constraints matrix is totally unimodular and the right hand side is comprised of integers, then it’s easy to find an integer solution. n Orgad Keller - Algorithms 2 - 26

Unimodular / Totally Unimodular Definition: A Unimodular matrix is a square matrix whose determinant is 0, 1 or -1. n Definition: A Totally Unimodular matrix is a matrix whose every non-singular square submatrix is unimodular. n Orgad Keller - Algorithms 2 - 27