Linear Programming Relaxations for Max Cut Wenceslas Fernandez

Linear Programming Relaxations for Max. Cut Wenceslas Fernandez de la Vega Claire Kenyon-Mathieu

Technique for approximation § § IP formulation with 0 -1 variables LP relaxation algorithm Strengthen LP: add valid inequalities Reduce integrality gap = § Better approximation

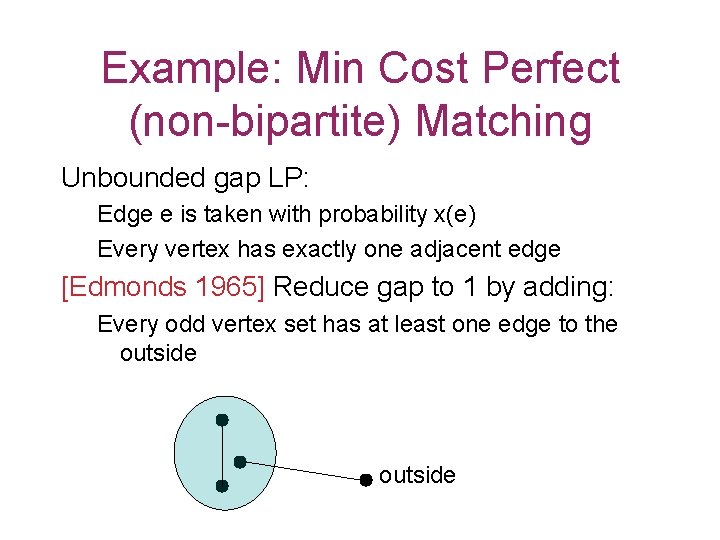
Example: Min Cost Perfect (non-bipartite) Matching Unbounded gap LP: Edge e is taken with probability x(e) Every vertex has exactly one adjacent edge [Edmonds 1965] Reduce gap to 1 by adding: Every odd vertex set has at least one edge to the outside

Lift and Project (L&P) [BCC, LS, SA, L] Systematic way to strengthen LPs. Rounds: • After 0 rounds: basic LP • After k rounds: contains all valid inequalities with support k • After n rounds: IP Poly-time solvable for any fixed k.

L&P and int gaps • Vertex cover [KG’ 98, AB, L’ 02, C’ 02 STT’ 06] • Max 3 SAT, Set cover, Hypergraph vertex cover [BOGH+03, AAT 05] Here: Maxcut Because: Theory people like Maxcut!

L&P for Max. Cut • LP relaxation has gap=2 [PT’ 94] • Thm [here]: gap is still 2 even after log(n)ˆc rounds of Sherali-Adams L&P • Thm [STT]: (for another LP) gap is still 2 even after a linear number of rounds of Lovasz. Shrijver L&P. • The moral: for Max. Cut, SDP is better than LP, even if the LPs are greatly enhanced.

Questions • Definition of L&P? • Differences Lovasz-Shrijver vs. Sherali. Adams vs. others? • SDP variant of L&P? • Compare proof to other lower bound proofs for L&P? No answers in this talk.

What I like about this work Not the result: somewhat unsurprising Not the “broader impacts”… The proof: Relatively clean: few short calculations, all driven by intuition Next: some key ideas for a simple case No need to know about lift and project!

Max. Cut LP relaxation… • x(i, j) indicates whether {i, j} crosses the cut x(i, j)+x(j, k)+x(k, i) ≤ 2 x(i, j) ≤ x(j, k)+x(k, i) i j • Gap = 2 k

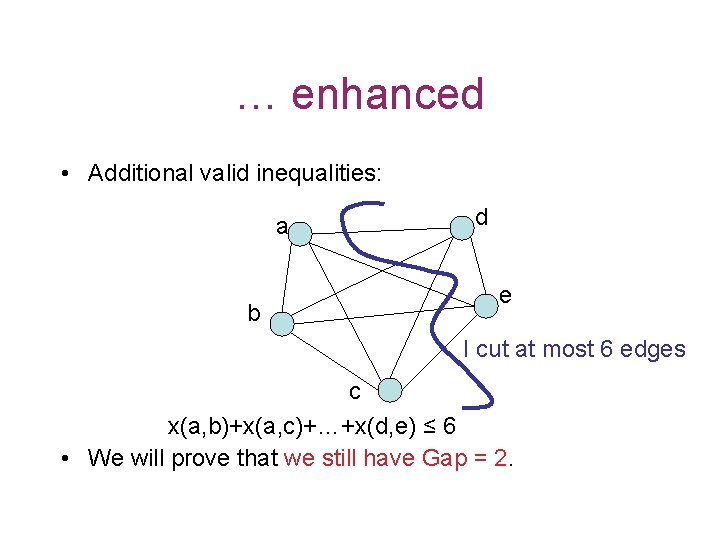
… enhanced • Additional valid inequalities: a b d e I cut at most 6 edges c x(a, b)+x(a, c)+…+x(d, e) ≤ 6 • We will prove that we still have Gap = 2.

• Graph: sparse random, altered for large girth. Gap=2! • Max. Cut ≈|E|/2 w. h. p. • To define x(i, j): threshold T. if distance > T then x(i, j)=1/2; else, construct a random labeling on the shortest path, and let x(i, j)=Pr(labels differ). • Such that x(i, j)=1 - for i and j adjacent FRAC ≈ |E|

Core of proof: feasibility • (x(i, j)) satisfies every constraint: let S be the vertices involved in ax-b 0. • Define a distribution over labels of S only, and let y(i, j)=Pr(labels differ). • y is a fractional cut, and constraint is valid inequality, so by definition ay-b ≥ 0: no calculations needed for this! • Observe that y(i, j) ≈ x(i, j) • Thus: ax-b ≈ ay-b ≥ 0.

Defining x(i, j) •

Defining y(i, j) when S={i, j, k, u, v} •

Coupling x(i, j) and y(i, j) •

Positive results Without SDP, is L&P actually useful? Thm [here]: in dense graphs, gap~1 after O(1) rounds of Sherali-Adams L&P Note: this is not surprising since there already exist at least 3 PTAS for Max. Cut in dense graphs.

Conclusion • L&P is potentially an attractive alternative to ad hoc fumbling with existing LPs • Unfortunately, most results so far are negative if we don’t use SDP. • To justify continued work on L&P, we need some positive results: for some problem, find a new, better approximation algorithm by using L&P explicitly and voluntarily.

That’s it • The end

Makespan minimization • Independent jobs, m parallel machines • LP: x(i, j) indicates whether job j goes on machine i, and t=makespan. Constraints: Every job must go on some machine Makespan greater than load on each machine • Unbounded gap • Add: “makespan≥p(j) for every job” reduces gap to 2, but this does not appear in L&P until after m rounds.

Proof(1/1) based on [AFKK]

Proof(4/4) • Given S set of 5 vertices or less, define (y(i, j)) over cuts of S • Subgraph H(S)={edges on some i-to-j path with i, j in S and distance < T} • Large girth H(S) is a forest • Remove each edge of H(S) w. p. 2 independently; In each connected component, label vertices alternating 1 and 0 from a random starting point Set Y(i, j)=1 iff i and j have different labels. set y(i, j)=Expectation of Y(i, j).