Fast SDP Relaxations of Graph Cut Clustering Transduction














- Slides: 19

Fast SDP Relaxations of Graph Cut Clustering, Transduction, and Other Combinatorial Problems (JMLR 2006) Tijl De Bie and Nello Cristianini Presented by Lihan He March 16, 2007

Outline Ø Statement of the problem Ø Spectral relaxation and eigenvector Ø SDP relaxation and Lagrange dual Ø Generalization: between spectral and SDP Ø Transduction and side information Ø Experiments Ø Conclusions

Statement of the problem Data set S: Affinity matrix A: Objective: graph cut clustering -- divide the data points into two set, P and N, such that No label: clustering With some labels: transduction

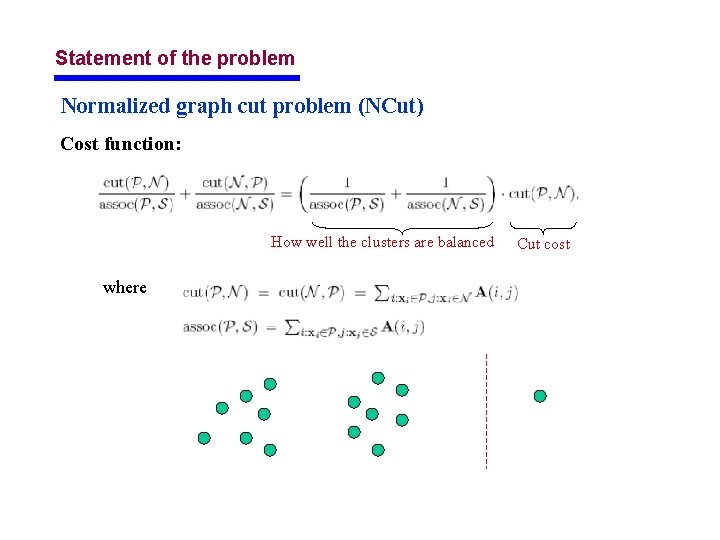
Statement of the problem Normalized graph cut problem (NCut) Cost function: How well the clusters are balanced where Cut cost

Statement of the problem Normalized graph cut problem (NCut) Unknown label vector Let Write Rewrite the NCut problem as a combinatorial optimization problem (1) NP-complete problem, the exponent is very high.

Spectral Relaxation Let the problem becomes Relax the constraints by adding and dropping the combinatorial constraints on , we obtain the spectral clustering relaxation (2)

Spectral Relaxation: eigenvector Solution: the eigenvector corresponding to the second smallest generalized eigenvalue. Solve the constrained optimization by Lagrange dual: The second constraint is automatically satisfied:

SDP Relaxation Let the problem becomes Note that Relax the constraints by adding the above constraints and dropping and Let and we obtain the SDP relaxation (3)

SDP Relaxation: Lagrange dual Lagrangian: We obtain the dual problem (strong dual is hold): (4) n+1 variables

Generalization: between spectral and SDP A cascade of relaxations tighter than spectral and looser than SDP where n constraints m constraints, Looser than SDP m+1 variables Design the structure of W design how to relax the constraints

Generalization: between spectral and SDP Ø rank(W)=n: original SDP relaxation. Ø rank(W)=1: m=1, W=d: spectral relaxation. Ø A relaxation is tighter than another if the column space of the matrix W used in the first one contains the full column space of W of the second. Ø If choose d within the column space of W, then all relaxations in the cascade are tighter than the spectral relaxation. Ø One approach of designing W proposed by the author: üSort the entries of the label vector (2 nd eigenvector) from spectral relaxation; üConstruct partition: m subsets are roughly equally large; üReorder the data points by this sorted order; üW … 1 2 m 1 … 1 W= ~ n/m 1 … 1 … 1

Transduction Given some labels, written as label vector yt -- transductive problem Reparameterize L= yt 0 Labeled 0 I Unlabeled Label constraints are imposed: Ø Rows (columns) corresponding to oppositely labeled training points then automatically are each other’s opposite; Ø Rows (columns) corresponding to same-labeled training points are equal to each other.

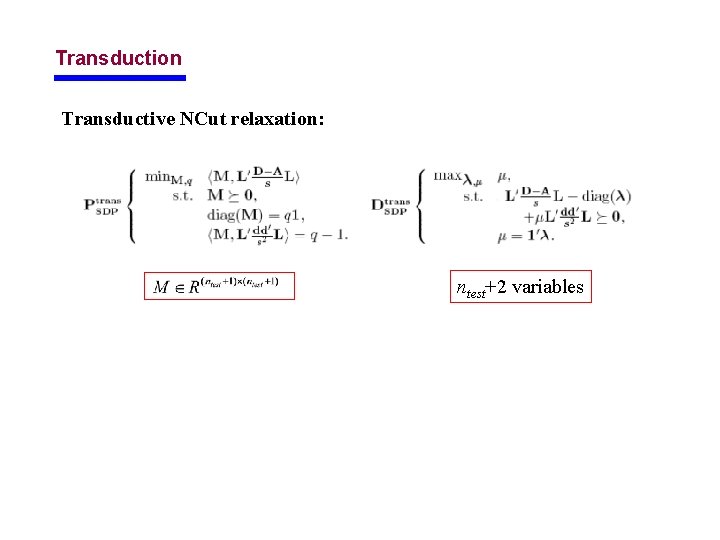
Transduction Transductive NCut relaxation: ntest+2 variables

General constraints Ø An equivalence constraint between two sets of data points specifies that they belong to the same class; Ø An inequivalence constraint specifies two set of data points to belong to opposite classes. Ø No detailed label information provided.

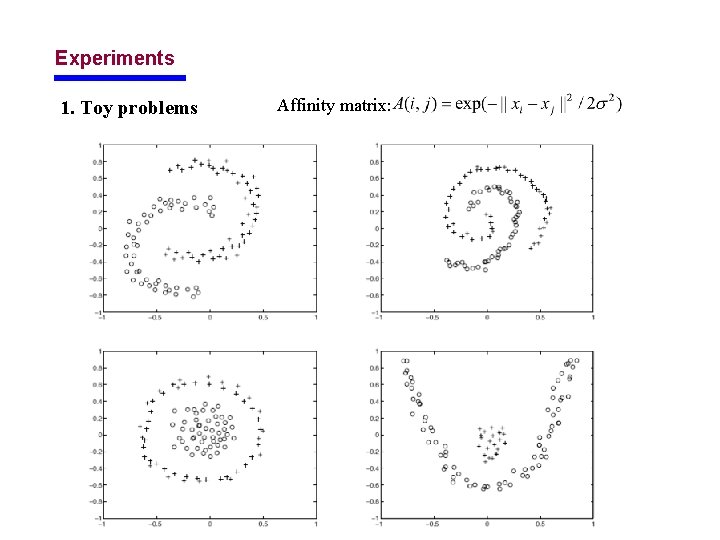
Experiments 1. Toy problems Affinity matrix:

Experiments 2. Clustering and transduction on text Data set: 195 articles 4 languages several topics Affinity matrix: 20 -nearest neighbor: A(i, j)= 1 0. 5 0 Distance of two articles: cosine distance on the bag of words representation Define dictionary

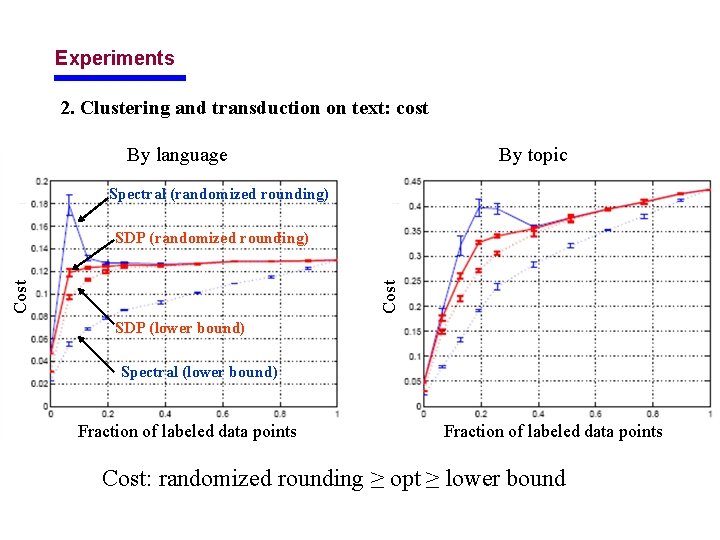
Experiments 2. Clustering and transduction on text: cost By language By topic Spectral (randomized rounding) Cost SDP (randomized rounding) SDP (lower bound) Spectral (lower bound) Fraction of labeled data points Cost: randomized rounding ≥ opt ≥ lower bound

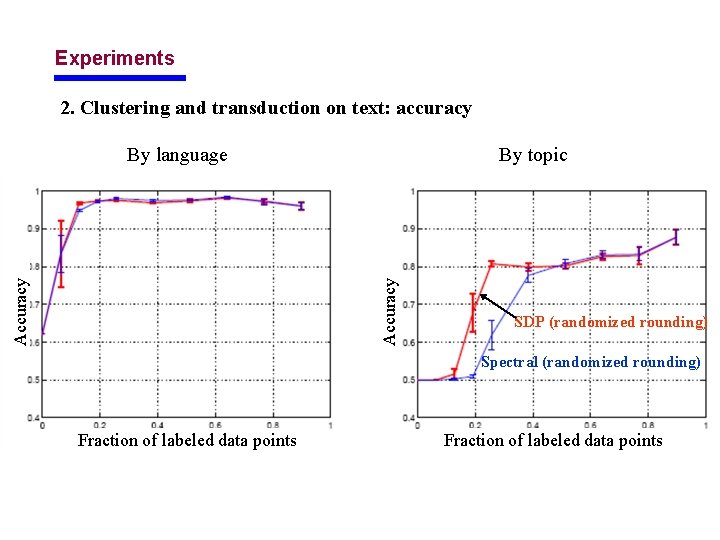
Experiments 2. Clustering and transduction on text: accuracy By topic Accuracy By language SDP (randomized rounding) Spectral (randomized rounding) Fraction of labeled data points

Conclusions Ø Proposed a new cascade of SDP relaxations of the NP-complete normalized graph cut optimization problem; Ø One extreme: spectral relaxation; Ø The other extreme: newly proposed SDP relaxation; Ø For unsupervised and semi-supervised learning, and more general constraints; Ø Balance the computational cost and the accuracy.
 Tableau des relaxations dynamiques
Tableau des relaxations dynamiques Bond energy algorithm
Bond energy algorithm Rumus distance
Rumus distance Flat and hierarchical clustering
Flat and hierarchical clustering Graclus
Graclus Cutaway example
Cutaway example Prolog disjunction
Prolog disjunction Cross cut vs rip cut teeth
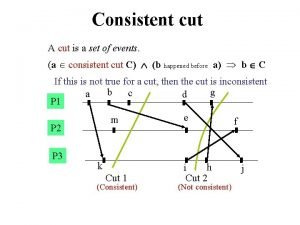
Cross cut vs rip cut teeth What is consistent cut in distributed system
What is consistent cut in distributed system Example of acid-fast bacteria
Example of acid-fast bacteria Acid fast and non acid fast bacteria
Acid fast and non acid fast bacteria Vertebrate sensory receptors
Vertebrate sensory receptors Transduction psychology
Transduction psychology 3 stages of signal transduction pathway
3 stages of signal transduction pathway Signal transduction
Signal transduction Olfactory transduction
Olfactory transduction Cell signal transduction
Cell signal transduction Cell communication pogil
Cell communication pogil Olfactory transduction
Olfactory transduction Generalized transduction
Generalized transduction