On linear and semidefinite programming relaxations for hypergraph

On linear and semidefinite programming relaxations for hypergraph matching (work appeared in SODA 10’) Yuk Hei Chan (Tom) joint work with Lap Chi Lau @ CUHK

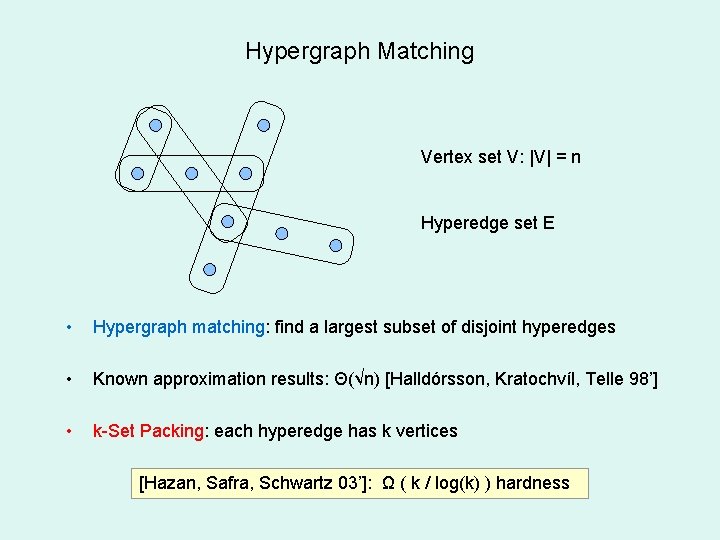
Hypergraph Matching Vertex set V: |V| = n Hyperedge set E • Hypergraph matching: find a largest subset of disjoint hyperedges • Known approximation results: Θ(√n) [Halldórsson, Kratochvíl, Telle 98’] • k-Set Packing: each hyperedge has k vertices [Hazan, Safra, Schwartz 03’]: Ω ( k / log(k) ) hardness

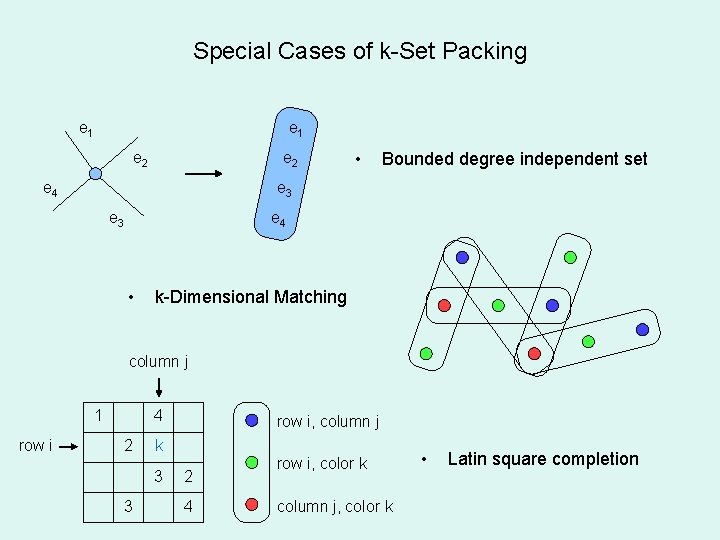
Special Cases of k-Set Packing e 1 e 2 e 4 • Bounded degree independent set e 3 e 4 • k-Dimensional Matching column j 1 row i 4 2 k 3 3 row i, column j 2 4 row i, color k column j, color k • Latin square completion

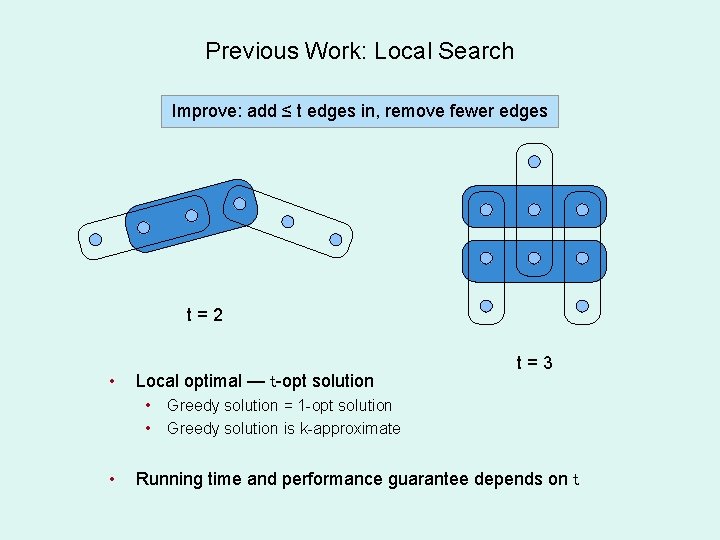
Previous Work: Local Search Improve: add ≤ t edges in, remove fewer edges t=2 • Local optimal — t-opt solution • • • t=3 Greedy solution = 1 -opt solution Greedy solution is k-approximate Running time and performance guarantee depends on t

Previous Work: Local Search Unweighted Hurkens, Schrijver 89’ Weighted Arkin, Hassin 97’ Chandra, Halldórsson 99’ Berman 00’ Berman, Krysta 03’ Ratio

Previous Work: Linear Programming Relaxation [Füredi 81’] integrality gap = k − 1 + 1/k (unweighted) [Füredi, Kahn, Seymour 93’] integrality gap = k − 1 + 1/k (weighted) • No projective plane as a sub-hypergraph — integrality gap k − 1 • Non-algorithmic, do not directly imply approximation algorithm

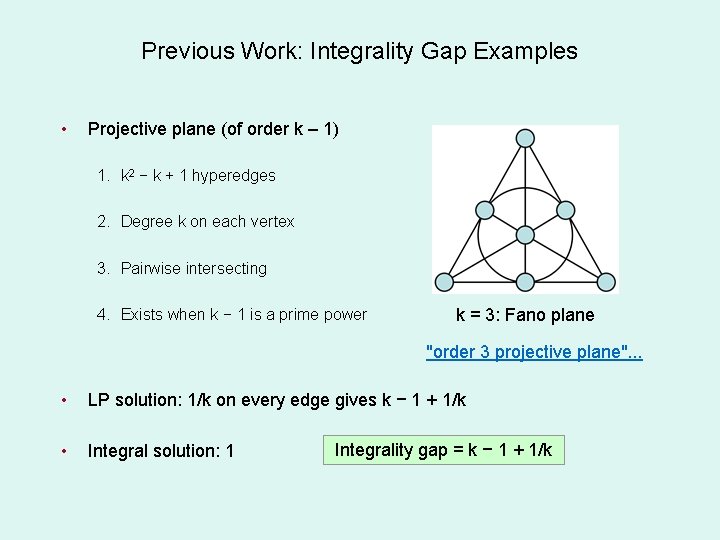
Previous Work: Integrality Gap Examples • Projective plane (of order k – 1) 1. k 2 − k + 1 hyperedges 2. Degree k on each vertex 3. Pairwise intersecting 4. Exists when k − 1 is a prime power k = 3: Fano plane "order 3 projective plane". . . • LP solution: 1/k on every edge gives k − 1 + 1/k • Integral solution: 1 Integrality gap = k − 1 + 1/k

Overview of New Results • Tight algorithmic analysis of the standard LP relaxation • Strengthening of LP by local constraints • • Fano LP & Sherali-Adams relaxation • Improvement but not much Strengthening of LP by global constraints • “Clique” LP & SDP • Improve by a constant factor over local constraints • New connection between local search and LP/SDP

Standard LP Relaxation Tight algorithmic analysis of the standard LP relaxation Algorithmic proof of gap k − 1 for k-Dimensional Matching k − 1 + 1/k for k-Set Packing Theorem 1: A 2 -approximation algorithm for weighted 3 -D Matching • Improve the local search algorithms by ε • New technique: iterative rounding + local ratio

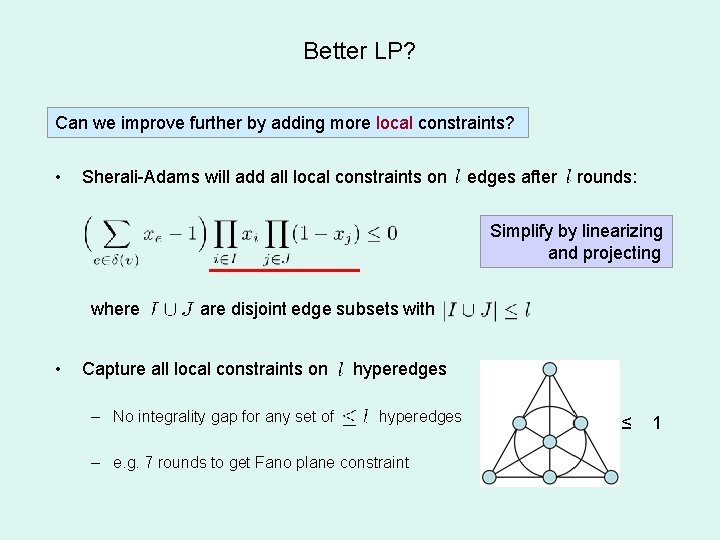
Better LP? Can we write a better LP? • For unweighted 3 -Set Packing, add Fano plane constraint: ≤ 1 • Main proof idea: in this Fano LP, any basic solution has no Fano plane! • Then apply Füredi’s result directly Theorem 2: Fano LP integrality gap = 2

Better LP? Can we improve further by adding more local constraints? • Sherali-Adams will add all local constraints on edges after rounds: Simplify by linearizing and projecting where • are disjoint edge subsets with Capture all local constraints on – No integrality gap for any set of hyperedges – e. g. 7 rounds to get Fano plane constraint ≤ 1

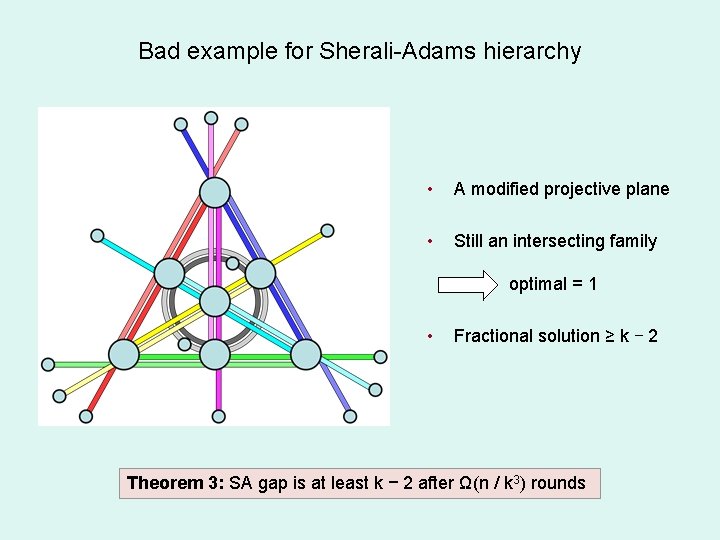
Bad example for Sherali-Adams hierarchy • A modified projective plane • Still an intersecting family optimal = 1 • Fractional solution ≥ k – 2 Theorem 3: SA gap is at least k − 2 after Ω(n / k 3) rounds

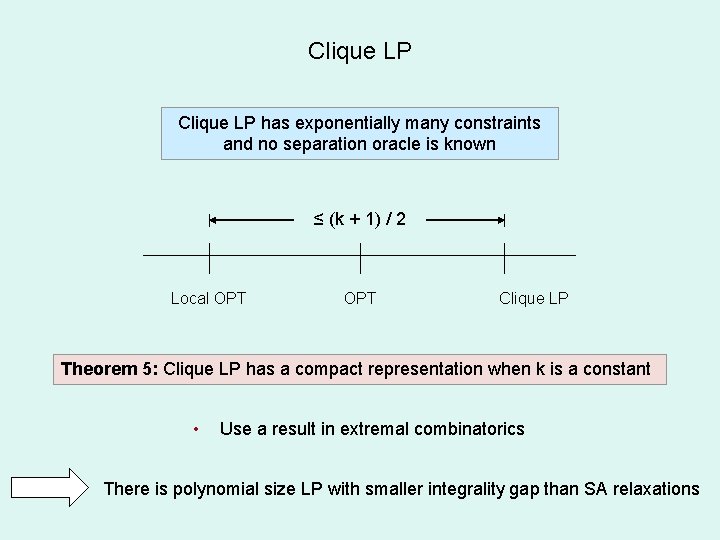
Global Constraints Clique constraint: for a set of intersecting edges, allow sum of values ≤ 1 Theorem 4: “Clique” LP integrality gap ≤ (k + 1) / 2 Some new connections between local search and LP/SDP relaxations ≤ (k + 1) / 2 Local OPT Extend local search analysis OPT Clique LP Non-constructive; no rounding algorithm

Clique LP has exponentially many constraints and no separation oracle is known ≤ (k + 1) / 2 Local OPT Clique LP Theorem 5: Clique LP has a compact representation when k is a constant • Use a result in extremal combinatorics There is polynomial size LP with smaller integrality gap than SA relaxations

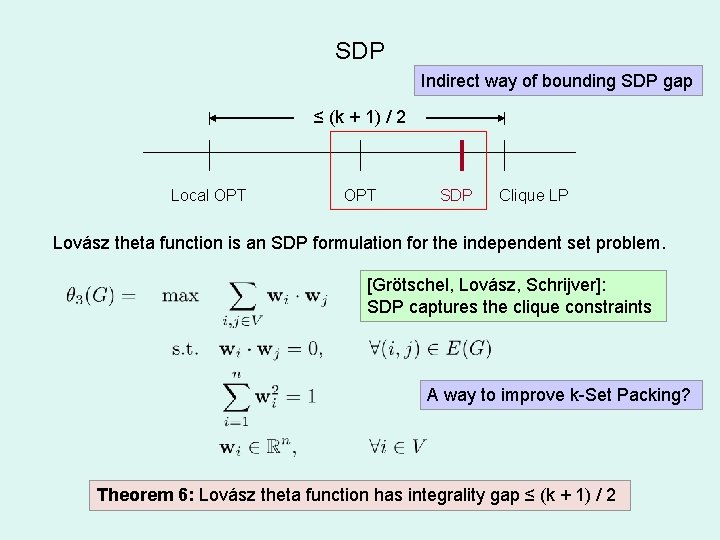
SDP Indirect way of bounding SDP gap ≤ (k + 1) / 2 Local OPT SDP Clique LP Lovász theta function is an SDP formulation for the independent set problem. [Grötschel, Lovász, Schrijver]: SDP captures the clique constraints A way to improve k-Set Packing? Theorem 6: Lovász theta function has integrality gap ≤ (k + 1) / 2

Details explained. . . 1. 2 -approximation for 3 -D matching 2. Integrality gap ≤ (k + 1) / 2 for clique LP

Approximation Algorithm for k-D Matching Theorem 1: A 2 -approximation algorithm for weighted 3 -D Matching 1. Compute a basic solution 2. Find a good ordering iteratively with small neighborhood 3. Use local ratio to compute an approximate solution Same algorithm for k-Set Packing gives k − 1 + 1/k

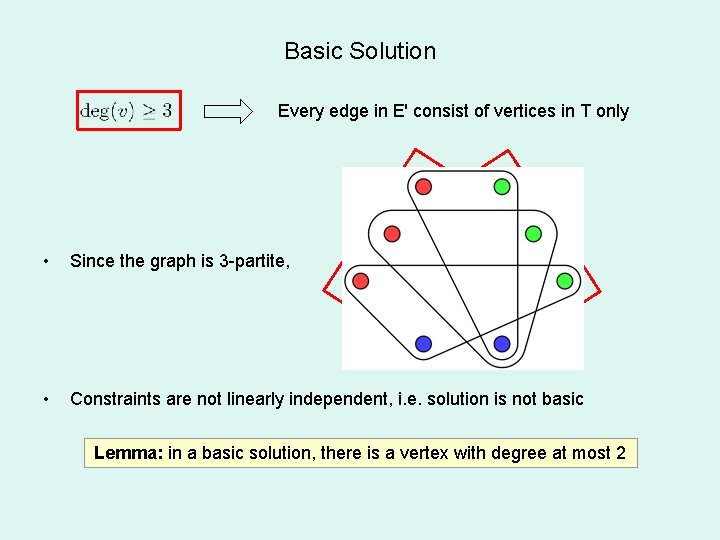
1. Basic Solution Only degree constraints can be tight. Delete edges with xe = 0. Basic solution: # variables ≤ # tight constraints in a basic solution Lemma: in a basic solution, there is a vertex with degree at most 2

Basic Solution Lemma: in a basic solution, there is a vertex with degree at most 2 Let T be the set of tight vertices, i. e. vertices s. t. Let E' be the set of non-zero edges, i. e. edges s. t. xe > 0 • Suppose not, then • Since each edge consists of 3 vertices, so • In a basic solution, , so

Basic Solution Every edge in E' consist of vertices in T only • Since the graph is 3 -partite, • Constraints are not linearly independent, i. e. solution is not basic Lemma: in a basic solution, there is a vertex with degree at most 2

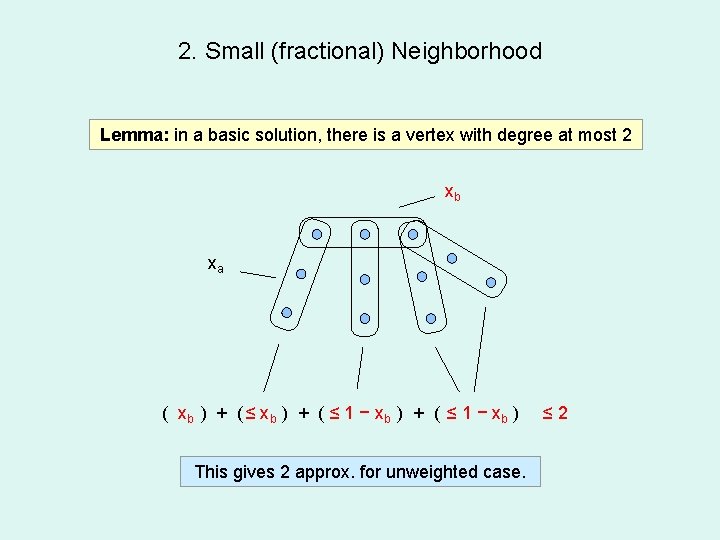
2. Small (fractional) Neighborhood Lemma: in a basic solution, there is a vertex with degree at most 2 xb xa ( xb ) + ( ≤ 1 − xb ) This gives 2 approx. for unweighted case. ≤ 2

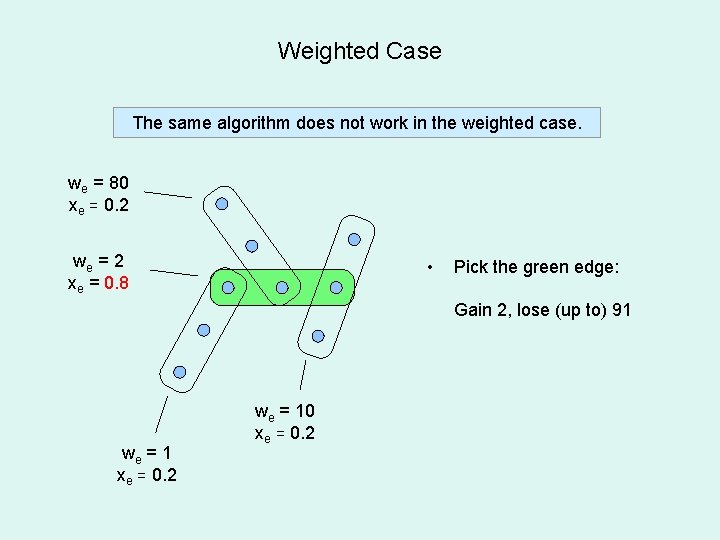
Weighted Case The same algorithm does not work in the weighted case. we = 80 xe = 0. 2 we = 2 xe = 0. 8 • Pick the green edge: Gain 2, lose (up to) 91 we = 1 xe = 0. 2 we = 10 xe = 0. 2

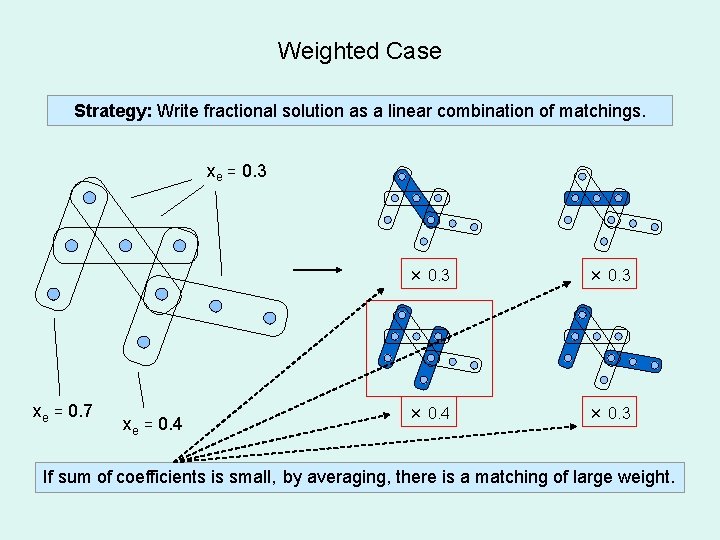
Weighted Case Strategy: Write fractional solution as a linear combination of matchings. xe = 0. 3 xe = 0. 7 xe = 0. 4 × 0. 3 × 0. 4 × 0. 3 If sum of coefficients is small, by averaging, there is a matching of large weight.

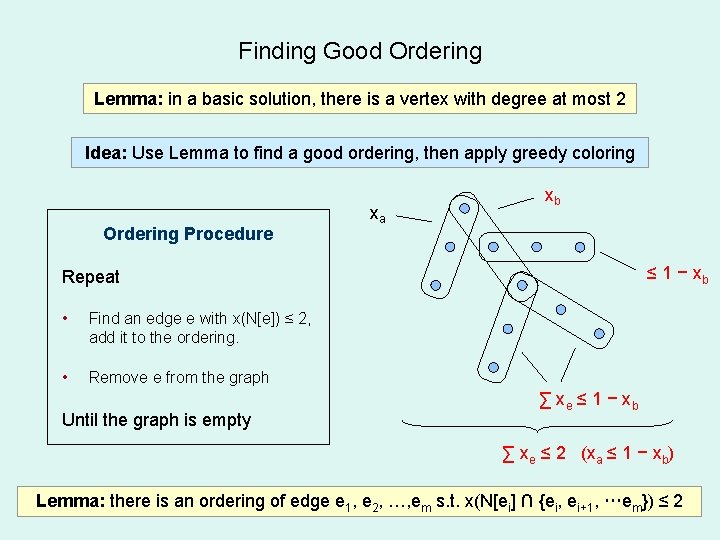
Finding Good Ordering Lemma: in a basic solution, there is a vertex with degree at most 2 Idea: Use Lemma to find a good ordering, then apply greedy coloring Ordering Procedure xa xb ≤ 1 − xb Repeat • Find an edge e with x(N[e]) ≤ 2, add it to the ordering. • Remove e from the graph Until the graph is empty ∑ xe ≤ 1 − x b ∑ xe ≤ 2 (xa ≤ 1 − xb) Lemma: there is an ordering of edge e 1, e 2, …, em s. t. x(N[ei] ∩ {ei, ei+1, …em}) ≤ 2

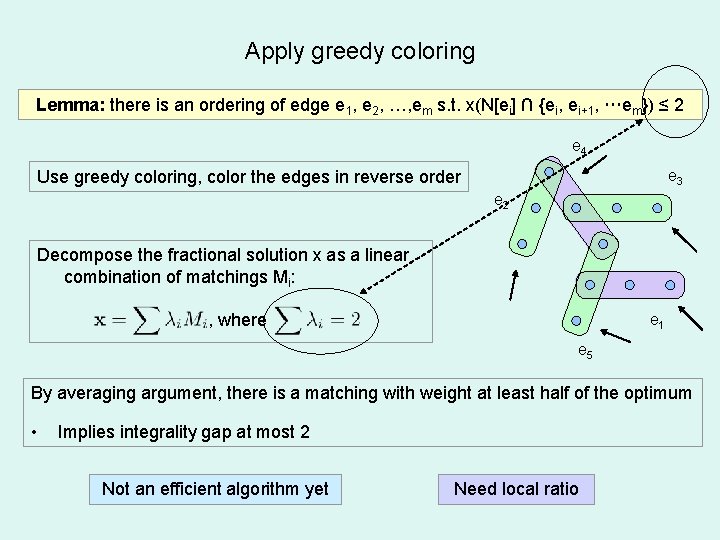
Apply greedy coloring Lemma: there is an ordering of edge e 1, e 2, …, em s. t. x(N[ei] ∩ {ei, ei+1, …em}) ≤ 2 e 4 e 3 Use greedy coloring, color the edges in reverse order e 2 Decompose the fractional solution x as a linear combination of matchings Mi: , where e 1 e 5 By averaging argument, there is a matching with weight at least half of the optimum • Implies integrality gap at most 2 Not an efficient algorithm yet Need local ratio

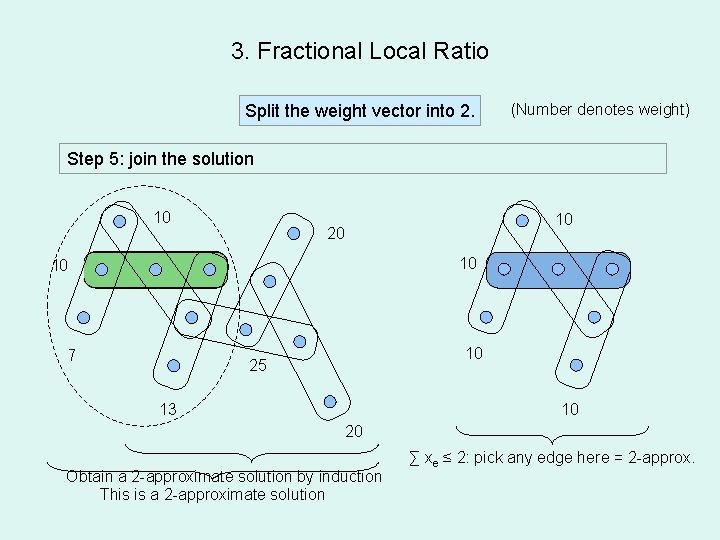
3. Fractional Local Ratio Split the weight vector into 2. (Number denotes weight) Step 5: 1: join 2: 3: 4: pick the make distribute remove ana edge solution copy non-positive the of with weight the∑graph xedges inand thesolve neighborhood closed the neighborhood residue of the instance blue (by edge Lemma) e ≤ 2 in 10 0 10 20 10 10 10 0 7 -3 10 25 13 3 10 20 Obtain a 2 -approximate solution by induction This is a 2 -approximate solution ∑ xe ≤ 2: pick any edge here = 2 -approx.

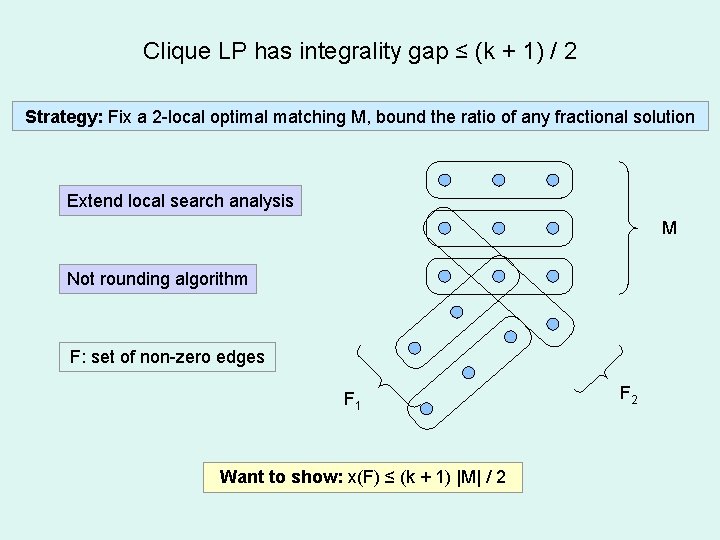
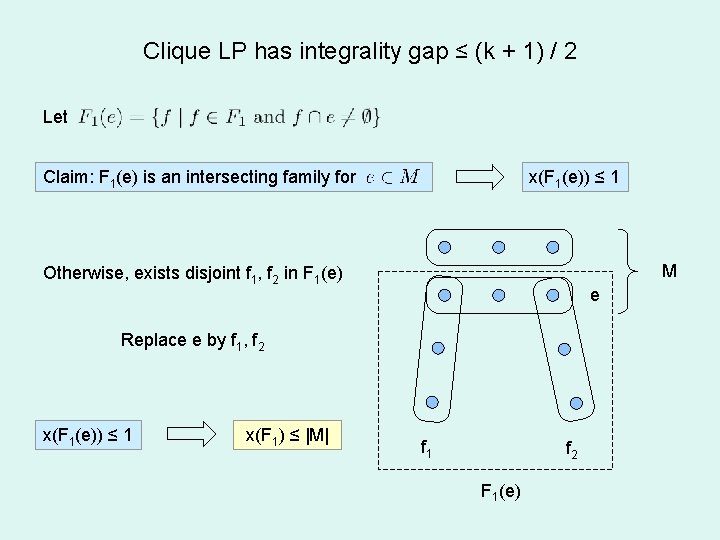
Clique LP has integrality gap ≤ (k + 1) / 2 Strategy: Fix a 2 -local optimal matching M, bound the ratio of any fractional solution Extend local search analysis M Not rounding algorithm F: set of non-zero edges F 1 Want to show: x(F) ≤ (k + 1) |M| / 2 F 2

Clique LP has integrality gap ≤ (k + 1) / 2 Let Claim: F 1(e) is an intersecting family for x(F 1(e)) ≤ 1 M Otherwise, exists disjoint f 1, f 2 in F 1(e) e Replace e by f 1, f 2 x(F 1(e)) ≤ 1 x(F 1) ≤ |M| f 1 f 2 F 1(e)

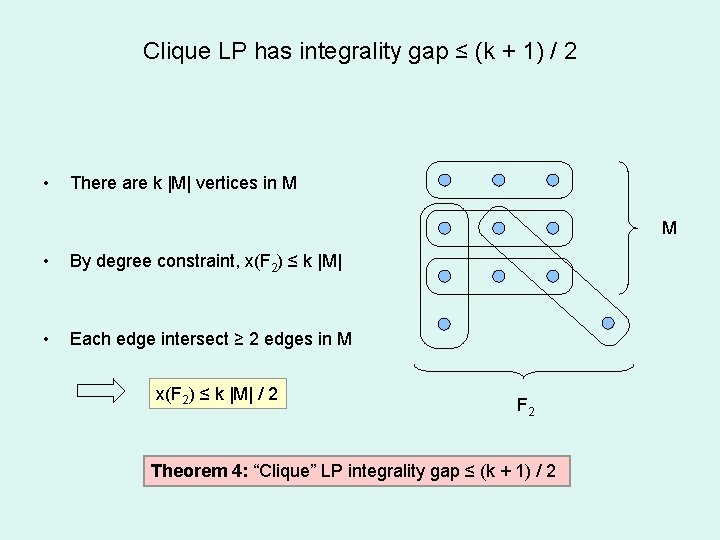
Clique LP has integrality gap ≤ (k + 1) / 2 • There are k |M| vertices in M M • By degree constraint, x(F 2) ≤ k |M| • Each edge intersect ≥ 2 edges in M x(F 2) ≤ k |M| / 2 F 2 Theorem 4: “Clique” LP integrality gap ≤ (k + 1) / 2

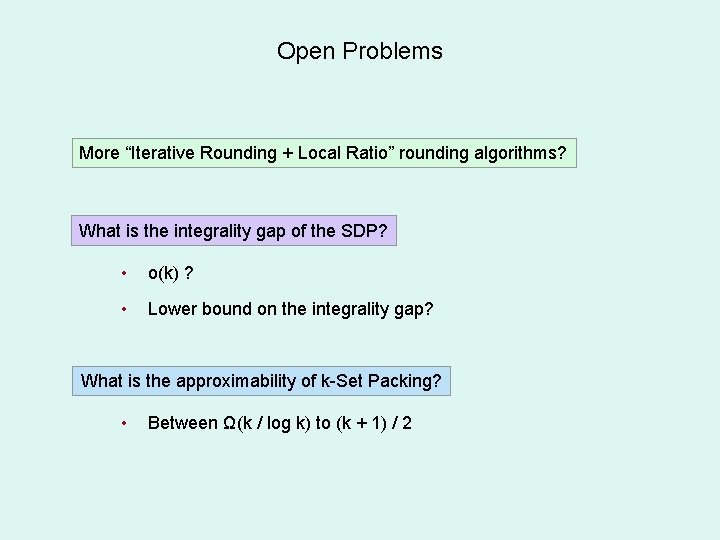
Open Problems More “Iterative Rounding + Local Ratio” rounding algorithms? What is the integrality gap of the SDP? • o(k) ? • Lower bound on the integrality gap? What is the approximability of k-Set Packing? • Between Ω(k / log k) to (k + 1) / 2

End