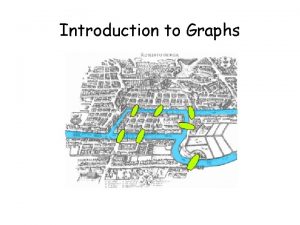
A generalization of quantum Steins Lemma Fernando G

A generalization of quantum Stein’s Lemma Fernando G. S. L. Brandão and Martin B. Plenio Tohoku University, 13/09/2008

(i. i. d. ) Quantum Hypothesis Testing n Given n copies of a quantum state, with the promise that it is described either by or , determine the identity of the state. n Measure two outcome POVM n Null probabilities hypothesis Error - Type I error: - Type II error: . Alternative hypothesis

(i. i. d. ) Quantum Hypothesis Testing n Given n copies of a quantum state, with the promise that it is described either by or , determine the identity of the state. n Measure two outcome POVM n Error probabilities - Type I error: The state is - Type II error: . The state is

(i. i. d. ) Quantum Hypothesis Testing n Given n copies of a quantum state, with the promise that it is described either by or , determine the identity of the state n Measure two outcome POVM n Error probabilities - Type I error: - Type II error:

(i. i. d. ) Quantum Hypothesis Testing n Several possible settings, depending on the constraints imposed on the probabilities of error n E. g. in symmetric hypothesis testing, Quantum Chernoff bound (Audenaert, Nussbaum, Szkola, Verstraete 07)

(i. i. d. ) Quantum Hypothesis Testing n Several possible settings, depending on the constraints imposed on the probabilities of error n E. g. in symmetric hypothesis testing, Quantum Chernoff bound (Audenaert, Nussbaum, Szkola, Verstraete 07)

(i. i. d. ) Quantum Hypothesis Testing n Several possible settings, depending on the constraints imposed on the probabilities of error n E. g. in symmetric hypothesis testing, Quantum Chernoff bound (Audenaert, Nussbaum, Szkola, Verstraete 07)

Quantum Stein’s Lemma n Asymmetric hypothesis testing n Quantum Stein’s Lemma (Hiai and Petz 91; Ogawa and Nagaoka 00)

Quantum Stein’s Lemma n Asymmetric hypothesis testing n Quantum Stein’s Lemma (Hiai and Petz 91; Ogawa and Nagaoka 00)

Quantum Stein’s Lemma n Most general setting - Null hypothesis (null): - Alternative hypothesis (alt. ):

Quantum Stein’s Lemma n Known results - (null) versus (alt. )

Quantum Stein’s Lemma n Known results - (null) versus (alt. )

Quantum Stein’s Lemma n Known results - (null) versus (alt. ) (Hayashi 00; Bjelakovic et al 04)

Quantum Stein’s Lemma n Known results - (null) versus (alt. ) (Hayashi 00; Bjelakovic et al 04) - Ergodic null hypothesis versus i. i. d. alternative hypothesis (Hiai and Petz 91)

Quantum Stein’s Lemma n Known results - (null) versus (alt. ) (Hayashi 00; Bjelakovic et al 04) - Ergodic null hypothesis versus i. i. d. alternative hypothesis (Hiai and Petz 91) - General sequence of states: Information spectrum (Han and Verdu 94; Nagaoka and Hayashi 07)

Quantum Stein’s Lemma n What about allowing the alternative hypothesis to be non-i. i. d. and to vary over a family of states? Only ergodicity and related concepts seems not to be enough to define a rate for the decay of (Shields 93)

Quantum Stein’s Lemma n What about allowing the alternative hypothesis to be non-i. i. d. and to vary over a family of states? Only ergodicity and related concepts seems not to be enough to define a rate for the decay of (Shields 93) This talk: A setting where the optimal rate can be determined for varying correlated alternative hypothesis

A generalization of Quantum Stein’s Lemma n Consider the following two hypothesis - Null hypothesis: For every we have - Alternative hypothesis: For every state 1. Each we have an unknown , where is closed and convex 2. Each contains the maximally mixed state 3. If , then 4. If and 5. If , then satisfies:

A generalization of Quantum Stein’s Lemma n Consider the following two hypothesis - Null hypothesis: For every we have - Alternative hypothesis: For every state 1. Each we have an unknown , where is closed and convex 2. Each contains the maximally mixed state 3. If , then 4. If and 5. If , then satisfies

A generalization of Quantum Stein’s Lemma n Consider the following two hypothesis - Null hypothesis: For every we have - Alternative hypothesis: For every state 1. Each we have an unknown , where is closed and convex 2. Each contains the maximally mixed state 3. If , then 4. If and 5. If , then satisfies

A generalization of Quantum Stein’s Lemma n theorem: Given , - (Direct Part) satisfying properties 1 -5 and there is a s. t.

A generalization of Quantum Stein’s Lemma n theorem: Given , - (Strong Converse) satisfying properties 1 -5 and s. t.

A motivation: Entanglement theory n We say is separable if If it cannot be written in this form, it is entangled n The sets of separable sates over satisfy properties 1 -5 , n The rate function of theorem is a well-known entanglement measure, the regularized relative (Vedral and Plenio 98) entropy of entanglement

Regularized relative entropy of entanglement n Given an entangled state (Vedral and Plenio 98) n n The theorem gives an operational interpretation to this measure as the optimal rate of discrimination of an entangled state to a arbitrary family of separable states More on the relative entropy of entanglement on Wednesday

Regularized relative entropy of entanglement n Cor: For every entangled state

Regularized relative entropy of entanglement n Rate of conversion of two states by local operations and classical communication: n The corollary implies that if n The mathematical definition of entanglement is equal to the operational: multipartite bound entanglement is real is entangled, For bipartite systems see Yang, Horodecki, Synak-Radtke 05

Some elements of the proofs n Asymptotic continuity: Let (Horodecki and Synak-Radtke 05; Christandl 06) n Non-lockability: Let (Horodecki 3 and Oppenheim 05)

Some elements of the proofs n Lemma: Let Then and s. t. and n Lemma: Let s. t. (Datta and Renner 08) , (Ogawa and Nagaoka 00)

Some elements of the proofs n Almost power states: n Exponential de Finetti theorem: For any permutationsymmetric state over there exists a measure and states s. t. (Renner 05)

Some elements of the proofs n Almost power states: n Exponential de Finetti theorem: For any permutationsymmetric state over there exists a measure and states s. t. (Renner 05)

Elements of the proof n (Proof sketch) We can write the statement of theorem as The dual formulation of the convex optimization above reads It is then clear that it suffices to prove

Elements of the proof n (Proof sketch) We can write the statement of theorem as The dual formulation of the convex optimization above reads It is then clear that it suffices to prove

Elements of the proof n (Proof sketch) We first show that for every Take Let sufficiently large such that be such that By the strong converse of quantum Stein’s Lemma As we find

Elements of the proof n (Proof sketch) We first show that for every Take Let sufficiently large such that be such that By the strong converse of quantum Stein’s Lemma As we find

Elements of the proof n (Proof sketch) We first show that for every Take Let sufficiently large such that be such that By the strong converse of quantum Stein’s Lemma As we find

Elements of the proof n (Proof sketch) We now show Let be an optimal sequence in the eq. above We can write Assuming conversely that the limit is zero, we find

Elements of the proof n (Proof sketch) We now show Let be an optimal sequence in the eq. above We can write Assuming conversely that the limit is zero, we find

Elements of the proof n (Proof sketch) We now show Let be an optimal sequence in the eq. above We can write Assuming conversely that the limit is zero, we find

Elements of the proof n (Proof sketch) We now show Let be an optimal sequence in the eq. above We can write Assuming conversely that the limit is zero, we find Then

Elements of the proof n (Proof sketch) We now show Let be an optimal sequence in the eq. above We can write Assuming conversely that the limit is zero, we find Then

Elements of the proof n (Proof sketch) Finally we now show with . Suppose conversely that . From we can write Note that we can take to be permutation-symmetric

Elements of the proof n (Proof sketch) Define We have We can write

Elements of the proof n (Proof sketch) Define We have We can write

Elements of the proof n (Proof sketch) Because Therefore we can write and with

Elements of the proof n (Proof sketch) Because Therefore we can write and with

Elements of the proof n (Proof sketch) Because Therefore we can write and with

Elements of the proof n (Proof sketch) Therefore with Finally

Elements of the proof n (Proof sketch) Because Therefore we can write and with