Ramsey Theory on the Integers and Reals Daniel




















- Slides: 20

Ramsey Theory on the Integers and Reals Daniel J. Kleitman and Jacob Fox MIT

Schur’s Theorem (1916) In every coloring of the positive integers with finitely many colors, there exists x, y, and z all the same color such that x + y = z. The following 3 -coloring of the integers [1, 13] does not have a monochromatic solution to x + y = z: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 However, every 3 -coloring of the integers [1, 14] has a monochromatic solution to x + y = z.

Partition Regularity A linear homogeneous equation a 1 x 1 + a 2 x 2 + … + a 3 x 3 = 0 (1) with integer coefficients is called r-regular if every r-coloring of the positive integers has a monochromatic solution to Equation (1) is called regular if it is r-regular for all positive integers r. Example: Schur’s theorem implies the equation x+y=z is regular.

The Equation x 1 + 2 x 2 – 5 x 3 = 0 Every 3 -coloring of the integers [1, 45] has a monochromatic solution to x 1 + 2 x 2 – 5 x 3 = 0. Therefore, the equation x 1 + 2 x 2 – 5 x 3 =0 is 3 -regular. Richard K. Guy, Unsolved problems in number theory. Third edition. Problem Books in Mathematics. Springer-Verlag, New York, 2004.

The Equation x 1 + 2 x 2 – 5 x 3 = 0 (Continued) If we color each positive integer n = m 5 k where 5 is not a factor of m by the remainder when m is divided by 5, then there are no monochromatic solutions to x 1 + 2 x 2 – 5 x 3 = 0 in this 4 -coloring of the positive integers. Therefore, the equation x 1 + 2 x 2 – 5 x 3 = 0 is 3 -regular, but not 4 -regular. Richard K. Guy, Unsolved problems in number theory. Third edition. Problem Books in Mathematics. Springer-Verlag, New York, 2004.

Rado’s Theorem (1933) Richard Rado’s thesis Studien zur Kombinatorik generalized Schur’s theorem by classifying those finite linear equations that are regular.

Studien zur Kombinatorik (1933)

Rado’s Theorem (1933) The equation a 1 x 1+a 2 x 2+…+ anxn =0 is regular if and only if some subset of the non-zero coefficients sums to 0.

Rado’s Boundedness Conjecture (1933) For every positive integer n, there exists an integer k=k(n) such that every linear homogeneous equation a 1 x 1+a 2 x 2+…+ anxn=0 that is k-regular is regular. Rado proved his conjecture in the trivial cases n = 1 and n = 2. Until recently, the conjecture has been open for n > 2.

Fox-Kleitman Theorem Every 24 -regular linear homogeneous equation a 1 + ax 2 + ax 3 = 0 is regular.

Partition Regularity over R A linear homogeneous equation a 1 x 1 + a 2 x 2 + … + a 3 x 3 = 0 (1) with real coefficients is called r-regular over R if every r-coloring of the nonzero real numbers has a monochromatic solution to Equation (1). A linear homogeneous equation is called regular over R if it is r-regular over R for all positive integers r.

Rado’s Theorem over R (1943) The equation a 1 x 1+a 2 x 2+…+ anxn =0 is regular over R if and only if some subset of the non-zero coefficients sums to 0. Regular examples: x 1 + x 2 - (1+ )x 3 = 0 x 1 - x 2 + 4 x 3 = 0 Nonregular example: x 1 + 2 x 2 - 4 x 3 = 0

The equation x 1 + 2 x 2 - 4 x 3 = 0 Let T denote the statement “the equation x 1 + 2 x 2 - 4 x 3 = 0 is 3 -regular over R. ” Jacob Fox and Rados Radoicic recently proved the statement T is independent of the Zermelo-Fraenkel axioms for set theory. That is, no contradiction arises if you assume T is true and no contradiction arises if you assume T is false.

Detour: Infinite numbers (Cardinals) We now assume the axiom of choice: for every family C of nonempty sets, there exists a function f defined on C such that f(S) is an element of S for every S from C. Two sets A and B are said to have the same size if there exists a bijective function f: A B. The cardinality of a set S is the size of S. • The cardinality of {a, b, c, d} is 4. • The cardinality of N is denoted by 0. • The cardinality of R is denoted by c.

The cardinals The cardinal numbers (in increasing order): 0, 1, 2, …, 0, 1, 2, …, , +1, … In 1873, Cantor proved that c > 0. So which one of the cardinals is c?

What is the Cardinality of the Continuum? Are there any cardinals between 0 and c? In other words, does c = 1? This is known as the continuum hypothesis. Cantor spent ten years of his life unsuccessfully trying to prove the continuum hypothesis. It is believed that this contributed to his mental illness later in life.

The Cardinality of the Continuum • In 1937, Kurt Gödel proved that the continuum hypothesis can not be proved false. • In 1963, Paul Cohen proved that the continuum hypothesis can not be proved true. In fact, for every positive integer n, it is independent of ZFC (Zermelo-Fraenkel axioms for set theory + Axiom of Choice) that c = n.

Countable Regularity A linear homogeneous equation a 1 x 1 + a 2 x 2 + … + a 3 x 3 = 0 (1) with real coefficients is called 0 -regular if every coloring of the real numbers by positive integers has a monochromatic solution to Equation (1) in distinct xi.

Countable Regularity Paul Erdős and Shizuo Kakutani in 1943 proved that the negation of the continuum hypothesis is equivalent to the equation x 1 + x 2 - x 3 - x 4 = 0 being 0 -regular. Fox recently classified which linear homogeneous equations are 0 -regular in terms of the cardinality of the continuum. For example, c 4 is equivalent to the equation x 1 + 3 x 2 - x 3 - x 4 – x 5 – x 6 = 0 being 0 -regular.

 Ramsey theory
Ramsey theory Jonbenet ramsey ransom note
Jonbenet ramsey ransom note Hyper reals
Hyper reals Ramsey theory
Ramsey theory Top man by james ramsey ullman
Top man by james ramsey ullman Regola di ramsey
Regola di ramsey Mnchoices assessment ramsey county
Mnchoices assessment ramsey county Regola di ramsey
Regola di ramsey Scala ramsey
Scala ramsey Araa baseball
Araa baseball Melissa ramsey fldoe
Melissa ramsey fldoe Top man by james ramsey ullman
Top man by james ramsey ullman Garrote jonbenet ramsey
Garrote jonbenet ramsey Lesson 4 tracking your expenses
Lesson 4 tracking your expenses Dave ramsey irregular income form
Dave ramsey irregular income form Brandon ramsey florida
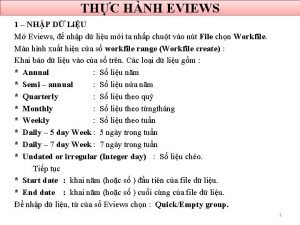
Brandon ramsey florida Kiểm định ramsey trong eviews
Kiểm định ramsey trong eviews Ramsey county child support
Ramsey county child support Evan ramsey alaska
Evan ramsey alaska Ramsey
Ramsey Patsy ramsey handwriting comparison
Patsy ramsey handwriting comparison