Introduction to the Hyper Reals An extension of

































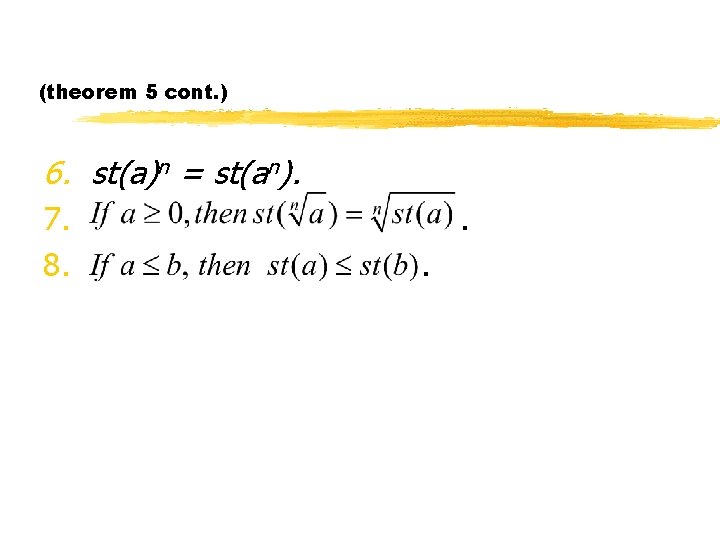



- Slides: 39

Introduction to the Hyper. Reals An extension of the Reals with infinitely small and infinitely large numbers.

Introduction to the Hyper. Reals z. Descriptive introduction z“Pictures” of the Hyper. Reals z. Axioms for the Hyper. Reals z. Some Properties (Theorems) of Hyper. Reals

Descriptive introduction z. A complete ordered field extension of the Reals (in a similar way that the Reals is a complete ordered field extension of the Rationals) z. Contains infinitely small numbers z. Contains infinitely large numbers z. Has the same logical properties as the Reals

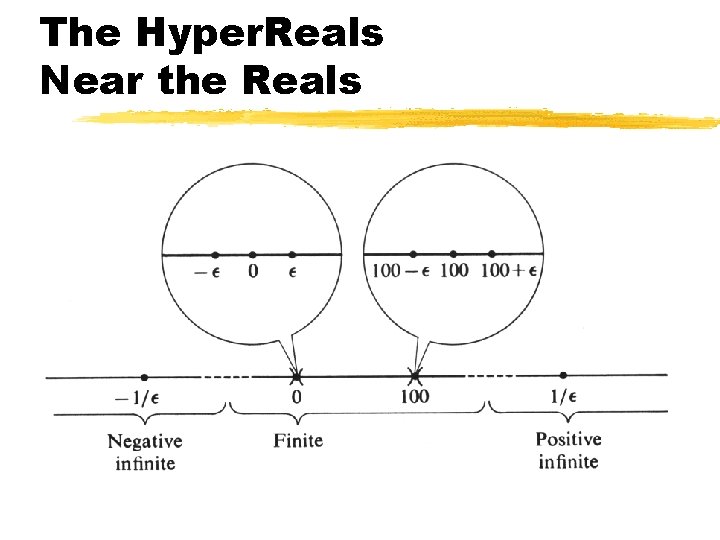
The Hyper. Reals Near the Reals

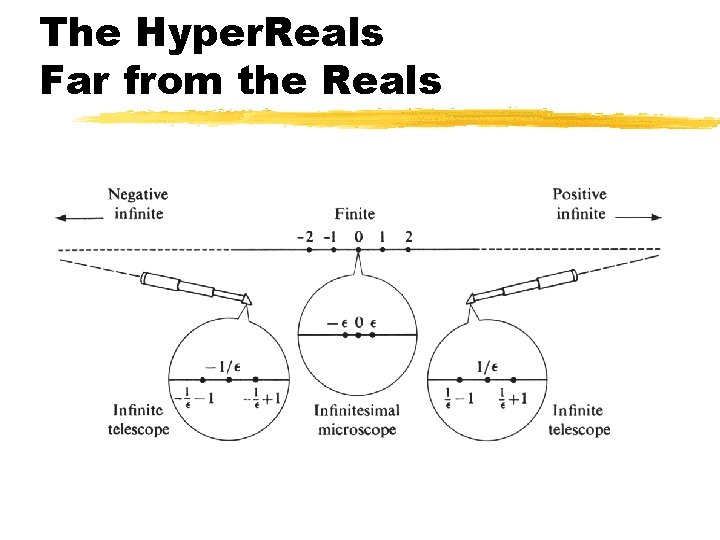
The Hyper. Reals Far from the Reals

Axioms for the Hyper. Reals z. Axioms common to the Reals y. Algebraic Axioms y. Order Axioms y. Completeness Axiom z. Axioms unique to the Hyper. Reals y. Extension Axiom y. Transfer Axiom

Algebraic Axioms z Closure laws: 0 and 1 are numbers. If a and b are numbers then so are a+b and ab. z Commutative laws: a + b = b + a and ab = ba z Associative laws: a + (b + c) = (a + b) +c and a(bc)=(ab)c z Identity laws: 0 + a = a and 1 a = a z Inverse laws: y For all a, there exists number –a such that a + (-a) = 0 and y if a 0, then there exist number a-1 such that a(a-1) = 1 z Distributive law: a( b+c ) = ab + ac

Order Axioms The is a set P of positive numbers which satisfies: z If x, y are elements of P then x + y is an element of P. z If x, y are elements of P then xy is an element of P. z If x is a number then exactly one of the following must hold: yx = 0, yx is an element of P or y-x is an element of P.

Definition of < and > za < b if and only if (b - a) is an element of P i. e. (b - a) is positive za > b if and only if b < a

Properties of < z 0 < 1 z Transitive law: If a<b and b<c then a<c. z Trichotomy law: Exactly one of the relations a<b, a = b, b<a, holds. z Sum law: If a<b, then a+c<b+c. z Product law: If a<b and 0<c, then ac<bc. z Root law: For a>0 and positive integer n, there is a number b>0 such that bn = a.

Completeness Axiom z A number b is said to be an upper bound of a set of numbers A if b x for all x in A. z A number c is said to be an least upper bound of the set of numbers A if c is an upper bound of A and b c for all upper bounds b of A. z. Completeness Axiom: z. Every non-empty set of numbers which is bounded above has a least upper bound.

Axioms unique to the Hyper. Reals z. Extension Axiom z. Transfer Axiom z Note: Actually these axioms are all that are needed as for the Hyper. Reals as the previous axioms can be derived from these two axioms.

Extension Axiom z The set R of real numbers is a subset of the set R* of hyperreal numbers. z The order relation <* on R* is an extension of the order < on R. z There is a hyperreal number such that 0 <* and <* r for each positive real number r. z For each real function f there is a given hyperreal function f* which has the following properties y domain(f) = R domain(f*) y f(x) = f*(x) for all x in domain(f) y range(f) = R range(f*) (Extension actually applies to any standard set built from the Reals. )

Transfer Axiom z (Function version) Every real statement that holds for one or more particular real functions holds for the hyperreal extensions of these functions z (Full version) Every standard statement (about sets built from the Reals) is true if and only if the corresponding non-standard statement (about sets built from Hyper. Reals - formed by adding the * operator) is true.

Example: Deriving the Commutative Laws from the Extension and Transfer Axioms z Commutative laws for the Reals: S: a R b R a+b=b+a and a • b=b • a. The Extension axiom gives us R*, +*, • *, and * and the Transfer axiom tells us that S*, the commutative laws for the Hyper. Reals is true. z Commutative laws for the Hyper. Reals: S*: a *R* b *R* a+*b=b+*a and a • *b=b • *a.

Definition: Infinitesimal A Hyper. Real number b is said to be: ypositive infinitesimal if b is positive but less than every positive real number. ynegative infinitesimal if b is negative but greater than every negative real number. yinfinitesimal if b is either positive infinitesimal, negative infinitesimal, or 0.

Definitions: Finite and Infinite A Hyper. Real number b is said to be: yfinite if b is between two real numbers. ypositive infinite if b is greater than every real number. ynegative infinite if b is smaller than every real number. yinfinite if b is positive infinite or negative infinite.

Theorem: The only real infinitesimal number is 0. z Proof: Suppose s is real and infinitesimal. Then exactly one of the following is true: s is negative, s = 0, or s is positive. If s is negative then it is a negative infinitesimal and hence r < s for all negative real numbers r. Since s is negative real then s < s which is nonsense. Thus s is not negative. Likewise if s is positive we get s < s. So s is not positive. Hence s = 0.

The Standard Part Principle z Theorem: For every finite Hyper. Real number b, there is exactly one real number r infinitely close to b. z Definition: If b is finite then the real number r, with r b, is called the standard part of b. We write r = std( b ).

Proof of the Standard Part Principle Uniqueness: Suppose r, s R and r b and s b. Hence r s. We have r-s is infinitesimal and real. The only real infinitesimal number is 0. Thus r-s = 0 which implies r = s.

Existence: Since b is finite there are real numbers s and t with s < b < t. Let A = { x | x is real and x < b }. A is non-empty since it contains s and is bounded above by t. Thus there is a real number r which is the least upper bound of A. We claim r b. Suppose not. Thus r b and Hence r-b is positive or negative. Case r-b is positive. Since r-b is not a positive infinitesimal there is a positive real s, s < r-b which implies b < r-s so that r-s is an upper bound of A. Thus r-s r but r-s < r. Thus r-b is not positive. Case r-b is negative. Since r-b is not a negative infinitesimal there is a negative real s, r-b<s which implies r-s < b so r-s is in A and hence r r-s but r < r-s, since s<0. Thus r-b is infinitesimal. So r b.

Infinite Numbers Exist Let be a positive infinitesimal. Thus 0 < < r for all positive real number r. Let r be a positive real number. Then so is 1/r. Therefore 0 < < 1/r and so 1/ > r. Let H = 1/ . Thus H > r for all positive real number r. Therefore H is an infinite number.

General Approach to Using the Hyper. Reals z Start with standard (Real) problem z Extend to non-standard (Hyper. Real) - adding * z Find solution of non-standard problem z Take standard part of solution to yield standard solution - removing * z Note: In practice we normally switch between Real and Hyper. Real without comment.

Theorem 1: Rules for Infinitesimal, Finite, and Infinite Numbers Th. Assume that e and d are infinitesimals; b, c are hyperreal numbers which are finite but not infinitesimal; and H, K are infinite hyperreal numbers; and n an integer. Then y. Negatives: x-e is infinitesimal. x-b is finite but not infinitesimal. x-H is infinite.

(Theorem cont) y. Reciprocals: x 1/e is infinite. x 1/b is finite but not infinitesimal. x 1/H is infinitesimal. y. Sums: xe +d is infinitesimal. xb+e is finite but not infinitesimal. xb+c is finite (possibly infinitesimal). x. H+e and H+b are infinite.

(Theorem cont) y. Products: xe*d and e*b are infinitesimal xb*c is finite but not infinitesimal. x. H *b and H*K are infinite. y. Roots: x. If e >0, x. If b>0, x. If H>0, is infinitesimal. is finite but not infinitesimal. is infinite.

(Theorem cont) y. Quotients: xe/ b, e/ H, and b/ H are infinitesimal xb/c is finite but not infinitesimal. xb/e , H/e, and H/b are infinite provided

Indeterminate Forms Examples Indeterminat infinitesimal e Form finite (equal to 1) infinite e/d e 2/e e/e 2 H/K H/H 2 H/H H 2/H H*e H*(1/H 2) H*(1/H) H 2*(1/H) H+K H+(-H) (H+1)+(-H) H+H

Theorem 2 1. Every hyperreal number which is between two infinitesimals is infinitesimal. 2. Every hyperreal number which is between two finite hyperreal numbers is finite. 3. Every hyperreal number which is greater than some positive infinite number is positive infinite. 4. Every hyperreal number which is less than some negative infinite number is negative infinite.

Definitions: Infinitely Close z. Two numbers x and y are said to be infinitely close ( written x y) if and only (x-y) is infinitesimal.

Theorem 3. Let a, b, and c be hyperreal numbers. Then 1. a a 2. If a b, then b a 3. If a b and b c then a b. (i. e. , is an equivalence relation. )

Theorem 4. Assume a b, Then 1. If a is infinitesimal, so is b. 2. If a is finite, so is b. 3. If a is infinite, so is b.

Definition: Standard Part Let b be a finite hyperreal number. The standard part of b, denoted by st(b), is the real number which is infinitely close to b.

Note this means: 1. st(b) is a real number 2. b = st(b) + for some infinitesimal . 3. If b is real then st(b) =b.

Theorem 5. Let a and b be finite hyperreal numbers. Then 1. 2. 3. 4. st(-a) = -st(a). st(a+b) = st(a) + st(b). st(a-b) = st(a) - st(b). st(ab) = st(a) * st(b). 5. If st(b) , then st(a/b) = st(a)/st(b).
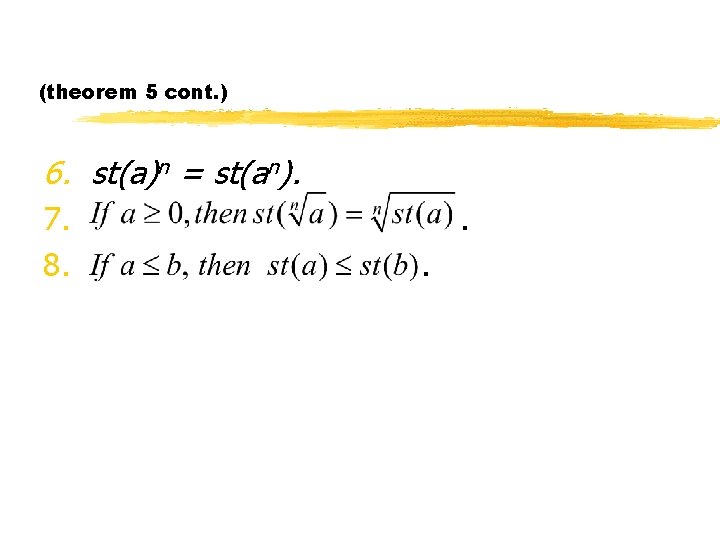
(theorem 5 cont. ) 6. st(a)n = st(an). 7. 8. . .

Example 1: st(a) Assume c 4 and c 4.

Example 2: st(a) Assume H is a positive infinite hyperreal number.

Example 3: st(a) Assume e is a nonzero infinitesimal.