Generalized Finite Element Methods Spring 2003 Properties of











![Theory Goals A posteriori error estimates: bound various “measures” of u[ exact solution]-uh [approximate Theory Goals A posteriori error estimates: bound various “measures” of u[ exact solution]-uh [approximate](https://slidetodoc.com/presentation_image_h/89bddbd310412053d74272d229579360/image-13.jpg)













- Slides: 32

Generalized Finite Element Methods Spring 2003 Properties of Galerkin approximations Suvranu De

Last class Equivalent representations of the mathematical model Strong formulation (BVP) Minimization statement Weak formulation (VBVP) Approximate solution techniques: Rayleigh Ritz Method Equivalence Galerkin Method Other techniques

This class Does the Galerkin method always work? (existence and uniqueness) How significantly does the approximate solution differ from the exact solution? (a priori error analysis) How fast does the approximate solution converge to the analytical solution? (rate of convergence)

The Galerkin Method VBVP • Takes the weak form (VBVP) as the starting point. • Very general. Works for problems that do not have a minimization principle. • For problems that do have a minimization principle, the Galerkin method and the Rayleigh-Ritz methods produce exactly the same set of discrete equations.

The Galerkin Method VBVP Approximation Pose the weak form: Find such that in the subspace Xh (APPROXIMATION) Find such that

The Galerkin Method VBVP Using the property of bilinearity and linearity as before

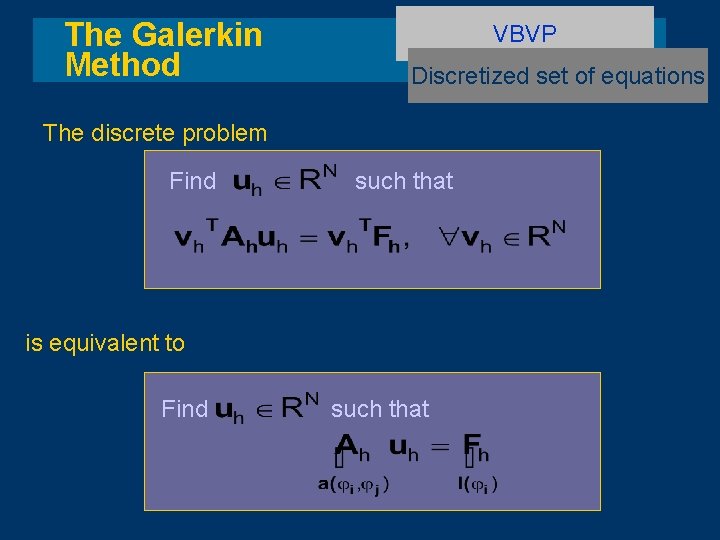
The Galerkin Method VBVP Discrete equations The discrete problem Find such that Choose First row

The Galerkin Method VBVP Discrete equations The discrete problem Find such that Choose Second row and so on. .

The Galerkin Method VBVP Discretized set of equations The discrete problem Find such that is equivalent to Find such that

Existence and uniqueness Definitions. . . A bilinear form b > 0 such that is continuous (bounded) if A bilinear form is elliptic if a > 0 such that Note that a elliptic bilinear form is always positive definite.

Existence and uniqueness Theorem We state without proof: Let Xh be a finite dimensional subspace of a Hilbert space X, a: Xh Xh R be a continuous elliptic bilinear form, and l: Xh R be a bounded linear functional. Then there exists a unique function uh Xh that satisfies Henceforth we will assume the bilinear form to be continuous and elliptic

Theory Goals A priori. . . A priori error estimates: bound various “measures” of u[ exact solution]-uh [approximate solution]; in terms of a constant C (function of W, problem parameters), h [some measure of discretization], and u Useful for: 1. Comparison of different discretizations ( which converges faster? ) 2. To understand the conditions that must be satisfied for rapid convergence 3. To understand if the method is properly implemented (to check a test problem for which the analytical solution is known)
![Theory Goals A posteriori error estimates bound various measures of u exact solutionuh approximate Theory Goals A posteriori error estimates: bound various “measures” of u[ exact solution]-uh [approximate](https://slidetodoc.com/presentation_image_h/89bddbd310412053d74272d229579360/image-13.jpg)
Theory Goals A posteriori error estimates: bound various “measures” of u[ exact solution]-uh [approximate solution]; in terms of a constant C (function of W, problem parameters), h [some measure of discretization], and uh More useful than a priori error estimators during the solution of practical problems (solution unknown). But much more difficult to obtain the constant C (needs additional computational effort)

Theory Error: Energy norm Definition. . . Define the energy norm ||| v ||| as: e. g. , for the Dirichlet problem hence For an elastic bar, this is twice the strain energy stored in the bar Note: ||| is problem dependent

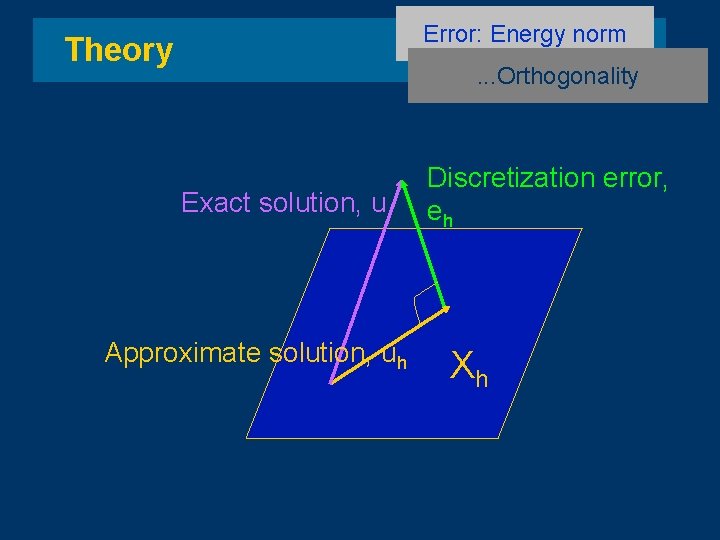
Theory Exact solution: u(x) X Approximate solution: uh(x) Xh Discretization error: Error: Energy norm. . . Definition

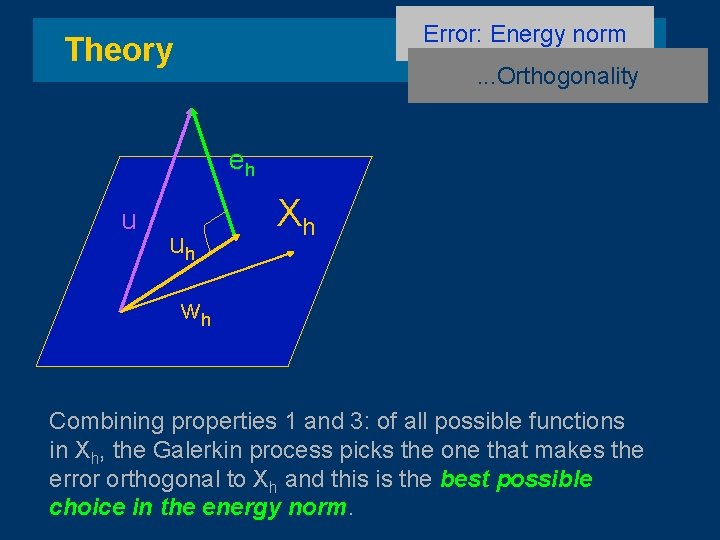
Theory Error: Energy norm Orthogonality. . . Property 1: The discretization error is orthogonal to the approximation space Xh in the energy norm Since then but Adding the last two equations

Error: Energy norm Theory . . . Orthogonality Exact solution, u Approximate solution, uh Discretization error, eh Xh

Theory Error: Energy norm General bound Property 2: Example: in the case of linear elasticity, this property means that the strain energy of the discretized model is always bounded from above by the strain energy of the mathematical model. Strain energy of mathematical model Strain energy of discretized model Increased refinement

Error: Energy norm Theory General bound Property 2: 0 Since a( , ) is SPD Therefore Bilinearity and symmetry

Theory Error: Energy norm Best approximation Property 3: Best approximation property In words: even if you knew the exact solution (u) you could not find a wh in Xh more accurate than uh in the energy norm “inf” means infinum

Error: Energy norm Theory . . . Orthogonality eh u uh Xh wh Combining properties 1 and 3: of all possible functions in Xh, the Galerkin process picks the one that makes the error orthogonal to Xh and this is the best possible choice in the energy norm.

Theory Error: Energy norm Property 3: Best approximation property For any Best approximation

Theory Error: H 1 norm Reminders. . The H 1 norm: measures e as well as ex

Theory Ellipticity of a( , ): Continuity of a( , ): Error: H 1 norm Reminders. .

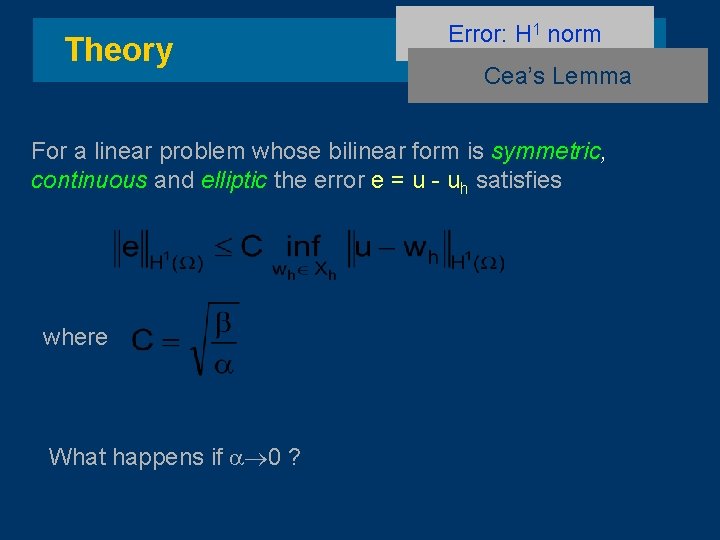
Theory Error: H 1 norm Cea’s Lemma For a linear problem whose bilinear form is symmetric, continuous and elliptic the error e = u - uh satisfies where What happens if a 0 ?

Theory Error: H 1 norm Cea’s Lemma From ellipticity: Property 3 Continuity

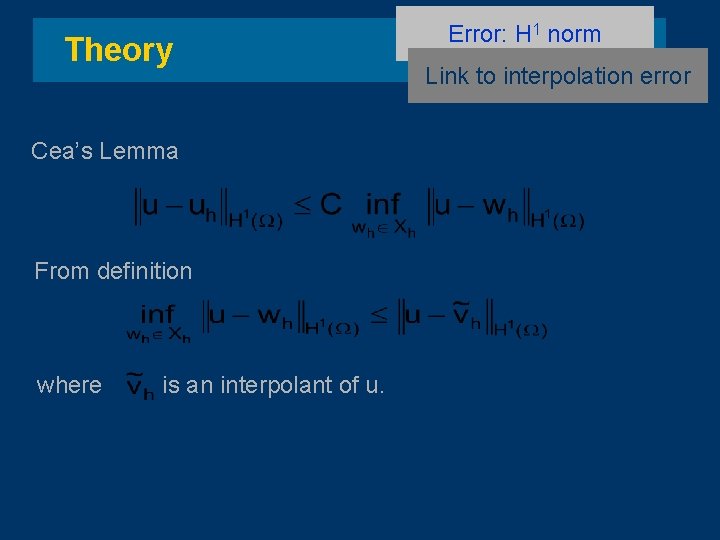
Theory Cea’s Lemma From definition where is an interpolant of u. Error: H 1 norm Link to interpolation error

Theory Error: H 1 norm Link to interpolation error Example : if Then we may choose any as a function that interpolates u at 4 points. This function has nothing to do with the approximate solution uh Leads to interpolation error estimate The problem of trying to determine how good our approximate solution is boils down to finding out the interpolation error ( )

Theory Error: H 1 norm Example Interpolation error estimate (from last slide) e. g. , piecewise linear interpolation (finite element) rate of convergence

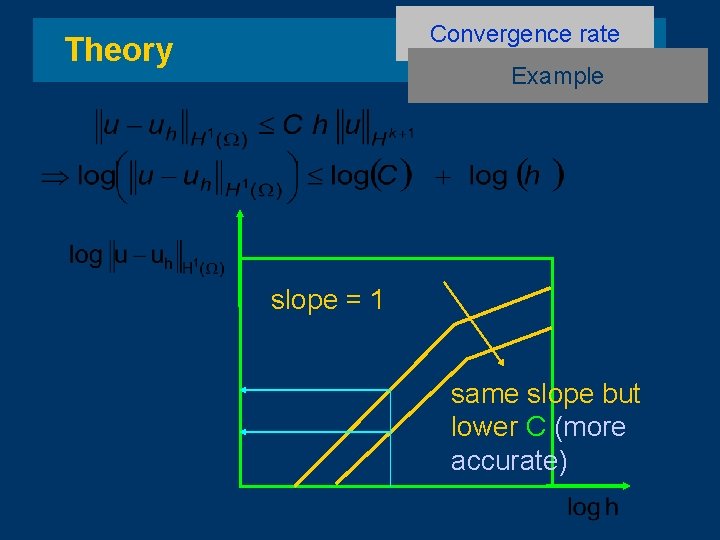
Convergence rate Theory Example slope = 1 same slope but lower C (more accurate)

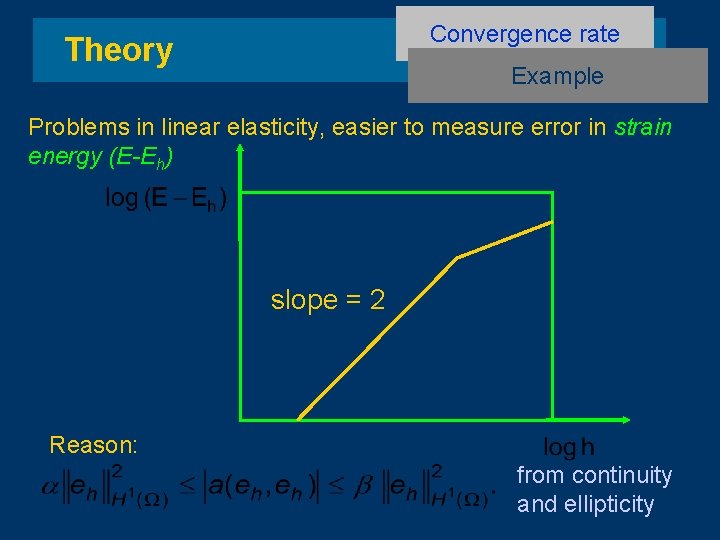
Convergence rate Theory Example Problems in linear elasticity, easier to measure error in strain energy (E-Eh) slope = 2 Reason: from continuity and ellipticity

Summary • Of all possible functions in Xh, the Galerkin process picks the one that makes the error orthogonal to Xh and this is the best possible choice in the energy norm. • Cea’s lemma is a expression of the error estimate in H 1 norm and allows us to link the error estimate to the interpolation error estimate. • If piece-wise Lagrange interpolation (of degree k) is used then the numerical solution exhibits an order k convergence in the H 1 norm (in the limit that ‘h’ is small) and an order 2 k convergence in the energy norm.
 Kim ki duk spring summer fall winter
Kim ki duk spring summer fall winter Finite element method
Finite element method Finite elements method
Finite elements method Finite subordinate clause
Finite subordinate clause Learning objectives for finite and non finite verbs
Learning objectives for finite and non finite verbs Learning objectives for finite and non finite verbs
Learning objectives for finite and non finite verbs Finite and nonfinite verbs
Finite and nonfinite verbs Finite and non finite
Finite and non finite Finite element method example
Finite element method example Hourglass modes finite element method
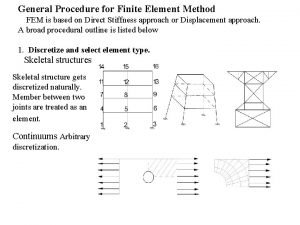
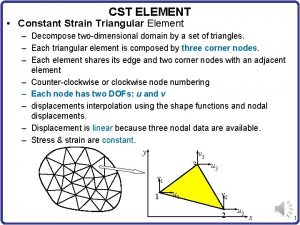
Hourglass modes finite element method Cst strain
Cst strain Truss finite element analysis
Truss finite element analysis Image preprocessing
Image preprocessing Finite element
Finite element Finite element analysis
Finite element analysis Difference between fea and fem
Difference between fea and fem Finite element method in geotechnical engineering
Finite element method in geotechnical engineering Finite element method
Finite element method Finite element method
Finite element method Finite element method
Finite element method Stifness formula
Stifness formula Spring summer autumn winter dates
Spring summer autumn winter dates Stiffness
Stiffness Fabrication of wax pattern
Fabrication of wax pattern Signal element vs data element
Signal element vs data element Signal element vs data element
Signal element vs data element Cst element shape function
Cst element shape function Atomic radius trend
Atomic radius trend Difference between intensive and extensive properties
Difference between intensive and extensive properties Physical properties and chemical properties
Physical properties and chemical properties One-period valuation model
One-period valuation model Generalized projection in dbms
Generalized projection in dbms Generalized projection in dbms
Generalized projection in dbms