8 EQUAES DIFERENCIAIS ORDINRIAS Parte 7 A 8

8. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Parte 7 A 8. 1–INTRODUÇÃO – PVI’s 8. 2–MÉTODOS DE PASSO SIMPLES 8. 3–MÉTODOS DE PASSO MÚLTIPLO 8. 4–MÉTODOS PREVISOR-CORRETOR 8. 5–EDOs DE ORDEM SUPERIOR 8. 6 -PVC’s E O MÉTODO DAS DIFERENÇAS FINITAS hoje

8. PVC’s e Diferenças Finitas 8. 5. 1. Introdução Seja um PVC de segunda ordem dado por: onde são constantes reais conhecidas, tais que nem , sejam nulas, simultaneamente.

8. PVC’s e Diferenças Finitas 8. 5. 1. Introdução O PVC de segunda ordem dado, tem a forma mais geral possível. o o Quando os valores de um PVC são dados na fronteira, por exemplo: dizemos que temos um problema de Dirichlet. Quando os valores da derivada de um PVC são dados na fronteira, por exemplo: dizemos que temos um problema de Neumann. P. G. Dirichlet (1805 -1858) e K. G. Neumann (1832 -1925)

8. PVC’s e Diferenças Finitas 8. 5. 1. Introdução Para o PVC de segunda ordem onde , dizemos que o PVC é homogêneo e a solução trivial é solução.

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização A idéia básica do Método de Diferenças Finitas transformar o PVC em um sistema de equações algébricas, aproximando as derivadas por Diferenças Finitas. Considere o intervalo do PVC dado por Fazemos. Fazendo uma partição Regular, sejam n subintervalos iguais de comprimento

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Assim, Notação: o o Se for linear em o sistema algébrico a ser resolvido será linear e podemos utilizar o Método de Lagrange para resolvê-lo. Se for não-linear em o sistema algébrico a ser resolvido será não-linear e podemos utilizar o Método de Newton para resolvê-lo.

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização As aproximações mais utilizadas para derivadas primeiras são: Diferença avançada Diferença atrasada Diferença centrada

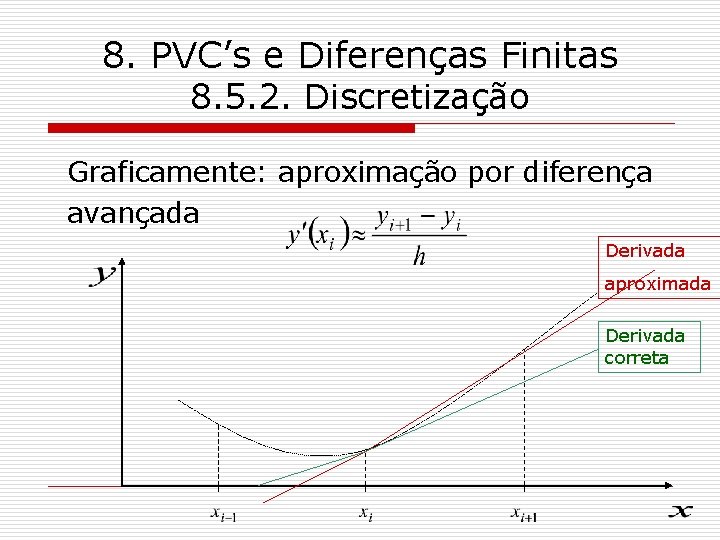
8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Graficamente: aproximação por diferença avançada Derivada aproximada Derivada correta

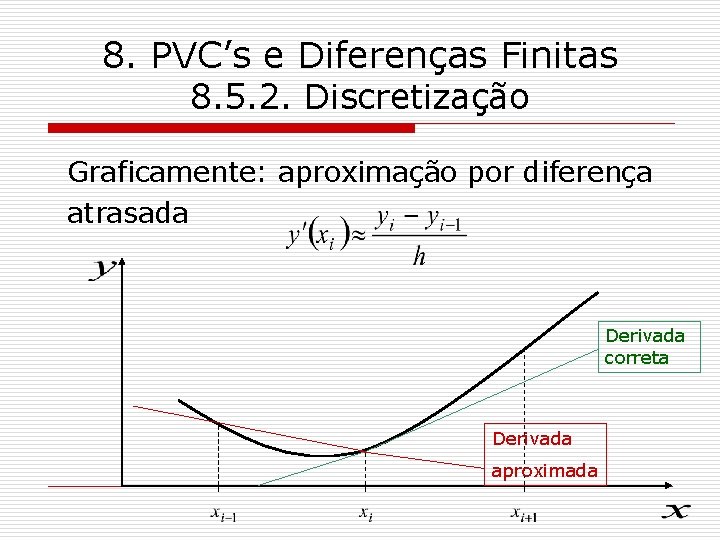
8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Graficamente: aproximação por diferença atrasada Derivada correta Derivada aproximada

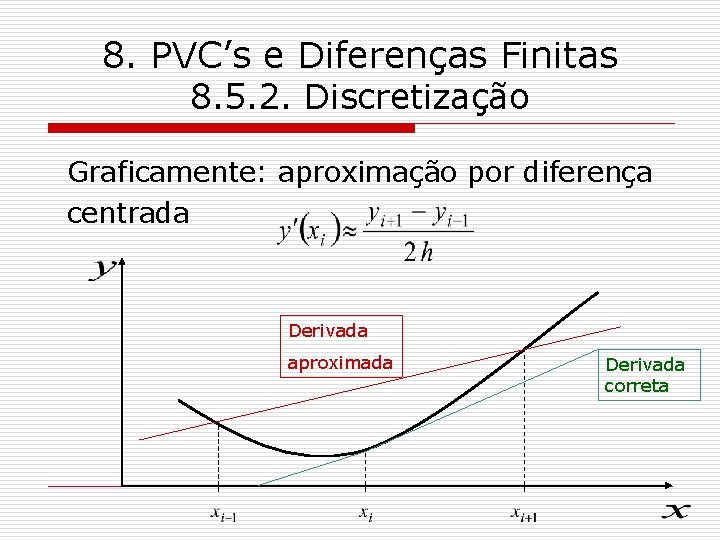
8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Graficamente: aproximação por diferença centrada Derivada aproximada Derivada correta

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Note que cometemos um erro ao aproximar a derivada pelas fórmulas discretas apresentadas. O erro cometido, da fórmula de Taylor, é Assim:

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Definição: Dizemos que uma constante é , se existe. Da definição, se , então a expressão de diferença avançada, para aproximar são de ordem , pois

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Analogamente, da definição, se então a expressão de diferença atrasada, para aproximar é de ordem , pois

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização Enfim, para diferença centrada temos que: Somando as aproximações

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização De modo que, a aproximação por diferença cen. Trada é de ordem. A fórmula de diferenças centradas é mais utilizada.

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização de derivadas segundas. Novamente a partir da série de Taylor, expandindo até a terceira ordem Somando as aproximações:

8. PVC’s e Diferenças Finitas 8. 5. 2. Discretização

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Exemplo 1: PVC linear Dividindo o intervalo [0, 1] em n subintervalos de comprimento h, segue que Como conhecemos resta calcular

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Utilizando diferenças centradas para a derivada primeira e a discretização deduzida para a derivada segunda, ou seja: e sendo ambas aproximações de segunda ordem, para cada i, a EDO discretizada fica

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Como reescrevemos a equação discreta A primeira equação (i=1), utilizando as condições no contorno, escreve-se como: Analogamente, para (i=n-1), temos a equação

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Temos que resolver o seguinte sistema linear Temos um sistema de n-1 equações, tridiagonal, a resolver, vejamos matricialmente:

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Reescrevendo matricialmente o sistema linear onde

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Note que matrizes tridiagonais são esparsas e neste caso não é conveniente utilizar métodos diretos para resolvê-las, ou seja, Método de Gauss, LU, Cholesky, entre outros. Métodos diretos provocam o preenchimento da matriz, ou seja, durante o processo de eliminação, os erros de truncamento, geram não-nulos em posições onde antes, originalmente, tínhamos termos nulos. Em matrizes esparsas deve-se utilizar métodos iterativos tipo Gauss-Seidel, associados a técnicas especiais para o armazenamento da matriz, as quais tiram proveito de sua esparsidade.

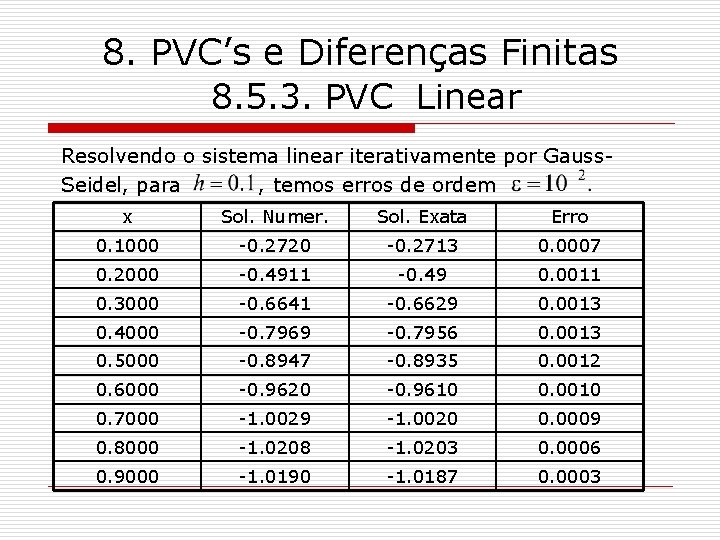
8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Resolvendo o sistema linear iterativamente por Gauss. Seidel, para , temos erros de ordem x Sol. Numer. Sol. Exata Erro 0. 1000 -0. 2720 -0. 2713 0. 0007 0. 2000 -0. 4911 -0. 49 0. 0011 0. 3000 -0. 6641 -0. 6629 0. 0013 0. 4000 -0. 7969 -0. 7956 0. 0013 0. 5000 -0. 8947 -0. 8935 0. 0012 0. 6000 -0. 9620 -0. 9610 0. 0010 0. 7000 -1. 0029 -1. 0020 0. 0009 0. 8000 -1. 0208 -1. 0203 0. 0006 0. 9000 -1. 0190 -1. 0187 0. 0003

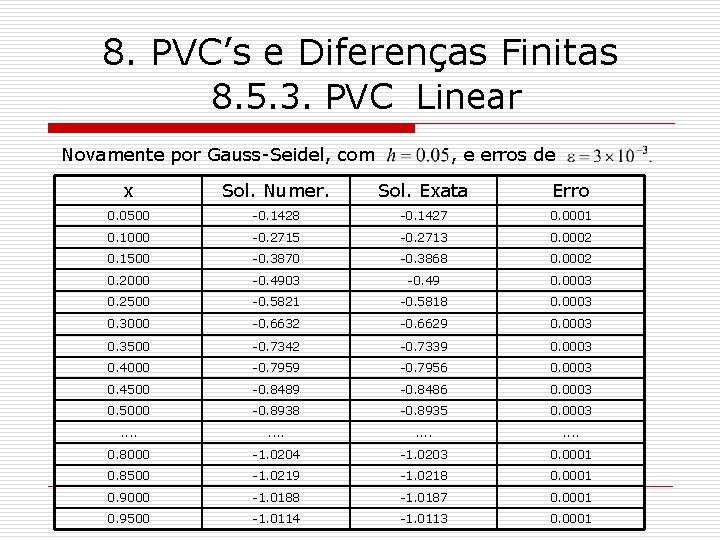
8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Novamente por Gauss-Seidel, com , e erros de x Sol. Numer. Sol. Exata Erro 0. 0500 -0. 1428 -0. 1427 0. 0001 0. 1000 -0. 2715 -0. 2713 0. 0002 0. 1500 -0. 3870 -0. 3868 0. 0002 0. 2000 -0. 4903 -0. 49 0. 0003 0. 2500 -0. 5821 -0. 5818 0. 0003 0. 3000 -0. 6632 -0. 6629 0. 0003 0. 3500 -0. 7342 -0. 7339 0. 0003 0. 4000 -0. 7959 -0. 7956 0. 0003 0. 4500 -0. 8489 -0. 8486 0. 0003 0. 5000 -0. 8938 -0. 8935 0. 0003 . . . . 0. 8000 -1. 0204 -1. 0203 0. 0001 0. 8500 -1. 0219 -1. 0218 0. 0001 0. 9000 -1. 0188 -1. 0187 0. 0001 0. 9500 -1. 0114 -1. 0113 0. 0001

8. PVC’s e Diferenças Finitas 8. 5. 4. PVC Não-Linear Exemplo 2: PVC não-linear Dividindo o intervalo [0, 1] em n subintervalos de comprimento h, segue que Como conhecemos resta calcular

8. PVC’s e Diferenças Finitas 8. 5. 4. PVC Não-Linear Utilizando diferenças centradas para a derivada primeira e a discretização deduzida para a derivada segunda, ou seja: e sendo ambas aproximações de segunda ordem, para cada i, a EDO discretizada fica

8. PVC’s e Diferenças Finitas 8. 5. 4. PVC Não-Linear Como reescrevemos a equação discreta A primeira equação (i=1), utilizando as condições no contorno, escreve-se como: Analogamente, para (i=n-1), temos a equação

8. PVC’s e Diferenças Finitas 8. 5. 4. PVC Não-Linear Temos que resolver o seguinte sistema linear Temos um sistema de n-1 equações, tridiagonal, a resolver. Utilize um método quase-Newton, por exemplo, para resolvê-lo.

8. PVC’s e Diferenças Finitas 8. 5. 5. PVC Condições Mistas o Quando temos condições mistas do tipo uma idéia é utilizar diferenças avançadas para descrever e deste modo a comdição de contorno escreve-se como:

8. PVC’s e Diferenças Finitas 8. 5. 5. PVC Condições Mistas Exemplo 3: PVC linear com condição mista Discretizando a EDO A primeira equação (i=1), utilizando as condições no contorno,

8. PVC’s e Diferenças Finitas 8. 5. 5. PVC Condições Mistas Exemplo 3: PVC linear com condição mista Discretizando a EDO A primeira equação (i=1), utilizando as condições no contorno,

8. PVC’s e Diferenças Finitas 8. 5. 5. PVC Condições Mistas Note que ao aproximar a derivada primeira na condição de contorno por diferença avançada, cometemos erros da ordem de. Poderíamos ter aproximado a derivada, na condição de contorno, por diferença centrada e com isto garantido erros da ordem Neste caso, temos que incluir um ponto a mais (x-1, y-1) nossa tabela e temos um sistema nxn

8. PVC’s e Diferenças Finitas 8. 5. 4. PVC Não-Linear Então temos o sistema com a condição Cuidado: deduzida para i=1, 2, . . , n-1 A primeira equação (i=0), utilizando a condição no contorno, escreve-se como:

8. PVC’s e Diferenças Finitas 8. 5. 3. PVC Linear Enfim, temos que resolver o seguinte sistema linear Temos um sistema de n equações, tridiagonal, a resolver.

Trabalho Final Seção 11. 4 – Burden – Faires Exercício Exercício 1 3 3 – a a Carolina – Everton – José – João – Vinícius