8 EQUAES DIFERENCIAIS ORDINRIAS Parte 1 8 1

8. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Parte 1 8. 1 – INTRODUÇÃO – PVI’s 8. 2 – MÉTODOS DE PASSO SIMPLES 8. 2. 1 – MÉTODO DE EULER hoje 8. 2. 2 – MÉTODOS DE TAYLOR 8. 2. 3 – MÉTODOS DE RUNGE-KUTTA 8. 3 – MÉTODOS DE PASSO MÚLTIPLO 8. 4 – MÉTODOS PREVISOR-CORRETOR 8. 5 – EDO’s DE ORDEM SUPERIOR E SISTEMAS DE EDO’s 8. 6 - PVC’s E O MÉTODO DAS DIFERENÇAS FINITAS

8. EDO’s 8. 1 INTRODUÇÃO o Problemas de Valores Iniciais (PVI’s) Se dada uma EDO de ordem n, a função, assim como suas derivadas até ordem n-1, são especificadas em um único ponto, então temos um problema a valores iniciais. Exemplo:

8. EDO’s 8. 1 INTRODUÇÃO o Problemas de Valores no Contorno (PVC’s) Se para uma dada EDO de ordem n, as n condições forem dadas em diferentes pontos, então temos um problema a valores no contorno. Ao contrário dos PVI’s, os PVC’s podem não apresentar unicidade de solução.

8. EDO’s 8. 1 INTRODUÇÃO o Exemplo de PVC’s. 1 - Seja um barra de comprimento L sujeita a uma carga uniforme q. Se em x=0 ela está fixada e em x=L ela está apoiada, então temos o problema

8. EDO’s 8. 1 INTRODUÇÃO o PVC’s sem unicidade na solução. 2 - O problema tem como solução

8. EDO’s 8. 1 INTRODUÇÃO o o Nesta primeira parte do estudo de EDO’s abordaremos métodos para resolução de PVI’s de primeira ordem. Dado o PVI construiremos , para simplificar igualmente espaçados, ou seja, e calculamos as aproximações neste pontos.

8. EDO’s 8. 1 INTRODUÇÃO o o Se para calcular , usamos apenas , então dizemos que o Método é de Passo Um ou de Passo Simples. Porém se usarmos mais valores teremos um Método de Passo Múltiplo. Para PVI’s de primeira ordem temos que é uma aproximação inicial para a solução. Problema auto-iniciante. Para Métodos de Passos Múltiplos devemos ter estratégias para as aprox. iniciais.

8. EDO’s 8. 1 INTRODUÇÃO o 1) Os Métodos de Passos Simples têm as seguintes características: Deve-se calcular os valores de e de suas derivadas em muitos pontos. Fator negativo. 2) A estimativa dos erros não é trivial.

8. EDO’s 8. 2. 1 Método de Euler o o o Considere o PVI Suponha que exista uma única solução do problema no intervalo de interesse. Reescrevendo (1) no ponto

8. EDO’s 8. 2. 1 Método de Euler Direto o o Aproximando a derivada em (2) pelo quociente de diferenças para frente (ou direto), obtemos Substituindo seus valores aproximados, temos a fórmula de Euler: por ,

8. EDO’s 8. 2. 1 Método de Euler Direto o Outra maneira para obter a fórmula de Euler é escrever o problema (1) como uma equação integral. Integrando (1) de

8. EDO’s 8. 2. 1 Método de Euler Direto o Se aproximarmos a integral substituindo E como , então

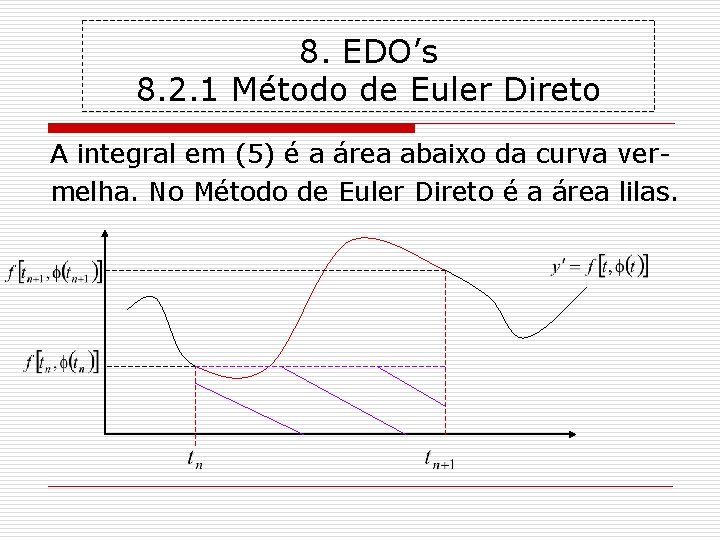
8. EDO’s 8. 2. 1 Método de Euler Direto A integral em (5) é a área abaixo da curva vermelha. No Método de Euler Direto é a área lilas.

8. EDO’s 8. 2. 1 Método de Euler Direto o o Note quanto menor forem as partições, melhor será a convergência do Método de Euler. O Erro da fórmula de Euler pode ser majorado através da fórmula de Taylor. Seja ERRO

8. EDO’s 8. 2. 1 Método de Euler Direto o Note que sendo então o erro devido ao truncamento de Euler é majorado por

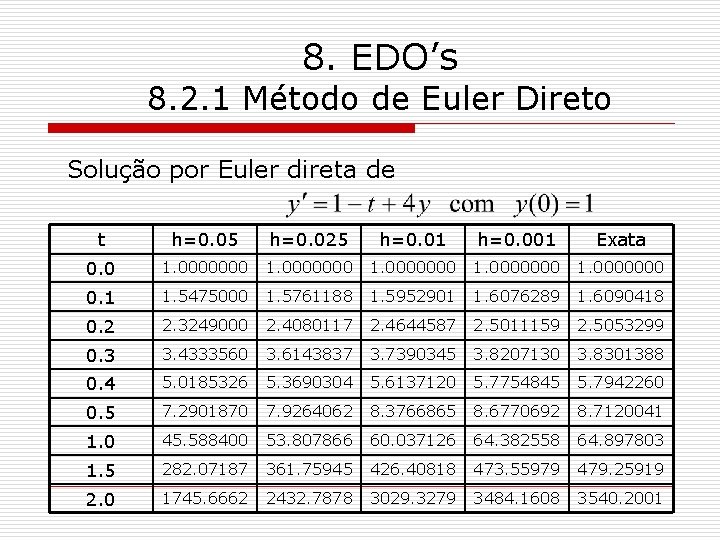
8. EDO’s 8. 2. 1 Método de Euler Direto o Exemplo 1: Considere o problema de valor inicial A solução exata é dada por Utilizando a fórmula de Euler (direta) e passos determine a solução do problema no intervalo

8. EDO’s 8. 2. 1 Método de Euler Direto Solução por Euler direta de t h=0. 05 h=0. 025 h=0. 01 h=0. 001 Exata 0. 0 1. 0000000 0. 1 1. 5475000 1. 5761188 1. 5952901 1. 6076289 1. 6090418 0. 2 2. 3249000 2. 4080117 2. 4644587 2. 5011159 2. 5053299 0. 3 3. 4333560 3. 6143837 3. 7390345 3. 8207130 3. 8301388 0. 4 5. 0185326 5. 3690304 5. 6137120 5. 7754845 5. 7942260 0. 5 7. 2901870 7. 9264062 8. 3766865 8. 6770692 8. 7120041 1. 0 45. 588400 53. 807866 60. 037126 64. 382558 64. 897803 1. 5 282. 07187 361. 75945 426. 40818 473. 55979 479. 25919 2. 0 1745. 6662 2432. 7878 3029. 3279 3484. 1608 3540. 2001

8. EDO’s 8. 2. 1 Método de Euler Direto o Note que os erros gerados em t=2. 0 são grandes! Para h=0. 001, ou seja, 2000 subintervalos, temos um erro acumulado de 1. 6% Como

8. EDO’s 8. 2. 1 Método de Euler Direto o O erro devido ao truncamento local é o Para ir de t=1. 95 a t=2. 0, quando h=0. 05, o Para obter um erro local de truncamento de 0. 01 neste problema necessitamos de h=0. 0006 em torno de t=2 e h=0. 03 em torno de t=0. Tais métodos com erros constante são chamados ADAPTATIVOS.

8. EDO’s 8. 2. 1 Método de Euler Inverso o Uma variante do método de Euler, chamado Método de Euler Inverso, consiste em aproximar a derivada em pelo quociente de diferenças para trás (ou inverso)

8. EDO’s 8. 2. 1 Método de Euler Inverso o Substituindo por seus valores aproximados, e fazendo temos a fórmula de Euler inversa o Note que a fórmula de Euler inversa fornece o valor de de forma implícita.

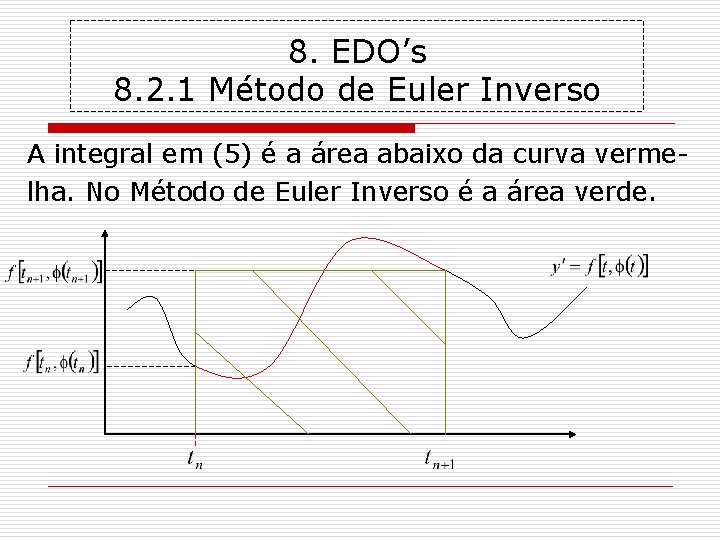
8. EDO’s 8. 2. 1 Método de Euler Inverso A integral em (5) é a área abaixo da curva vermelha. No Método de Euler Inverso é a área verde.

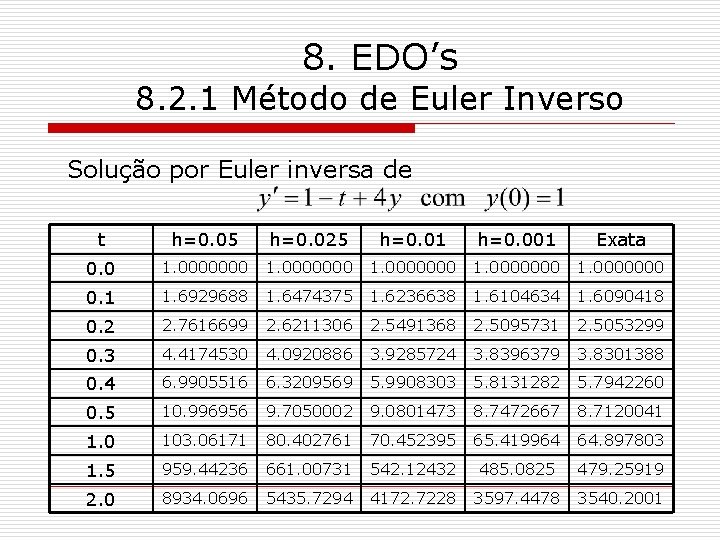
8. EDO’s 8. 2. 1 Método de Euler Inverso o Exemplo 2: Considere o problema de valor inicial A solução exata é dada por Utilizando a fórmula de Euler (inversa) e passos determine a solução do problema no intervalo

8. EDO’s 8. 2. 1 Método de Euler Inverso Solução por Euler inversa de é dada pela fórmula de Euler inversa O primeiro passo gera: Continuando, temos a tabela:

8. EDO’s 8. 2. 1 Método de Euler Inverso Solução por Euler inversa de t h=0. 05 h=0. 025 h=0. 01 h=0. 001 Exata 0. 0 1. 0000000 0. 1 1. 6929688 1. 6474375 1. 6236638 1. 6104634 1. 6090418 0. 2 2. 7616699 2. 6211306 2. 5491368 2. 5095731 2. 5053299 0. 3 4. 4174530 4. 0920886 3. 9285724 3. 8396379 3. 8301388 0. 4 6. 9905516 6. 3209569 5. 9908303 5. 8131282 5. 7942260 0. 5 10. 996956 9. 7050002 9. 0801473 8. 7472667 8. 7120041 1. 0 103. 06171 80. 402761 70. 452395 65. 419964 64. 897803 1. 5 959. 44236 661. 00731 542. 12432 485. 0825 479. 25919 2. 0 8934. 0696 5435. 7294 4172. 7228 3597. 4478 3540. 2001

8. EDO’s 8. 2. 1 Método de Euler Aprimorado Note que tanto o método de Euler direto quanto o inverso geram erros acumulativos quando t cresce. No exemplo o erro foi da ordem de 1. 2%. q Os Métodos adaptativos de Euler são uma solução, contudo teremos uma sub-rotina para calcular o tamanho do passo para cada n. q Fórmula de Euler Aprimorada ou centrada aproxima a função f na integral por uma média. q

8. EDO’s 8. 2. 1 Método de Euler Aprimorado q q A fórmula de Euler Aprimorada escrevese como: Os erros são menores e convergência é mais rápida neste caso.

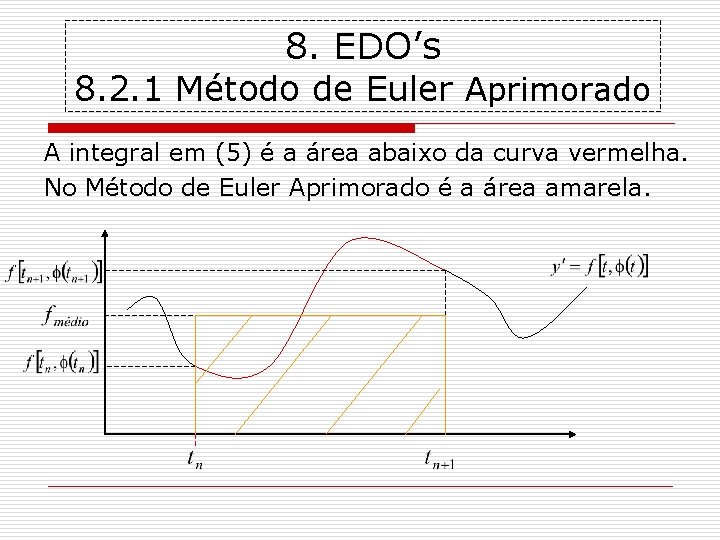
8. EDO’s 8. 2. 1 Método de Euler Aprimorado A integral em (5) é a área abaixo da curva vermelha. No Método de Euler Aprimorado é a área amarela.

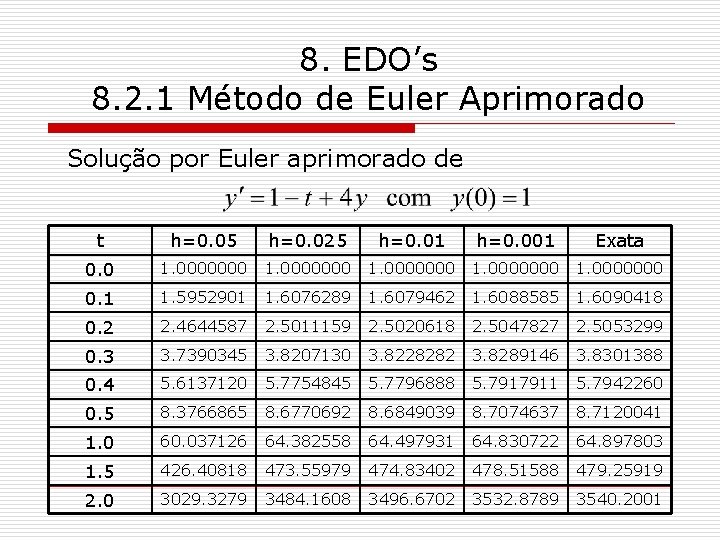
8. EDO’s 8. 2. 1 Método de Euler Aprimorado A solução por Euler Aprimorado de é dada pela fórmula também conhecida como fórmula de Heun. Calculando temos a tabela:

8. EDO’s 8. 2. 1 Método de Euler Aprimorado Solução por Euler aprimorado de t h=0. 05 h=0. 025 h=0. 01 h=0. 001 Exata 0. 0 1. 0000000 0. 1 1. 5952901 1. 6076289 1. 6079462 1. 6088585 1. 6090418 0. 2 2. 4644587 2. 5011159 2. 5020618 2. 5047827 2. 5053299 0. 3 3. 7390345 3. 8207130 3. 8228282 3. 8289146 3. 8301388 0. 4 5. 6137120 5. 7754845 5. 7796888 5. 7917911 5. 7942260 0. 5 8. 3766865 8. 6770692 8. 6849039 8. 7074637 8. 7120041 1. 0 60. 037126 64. 382558 64. 497931 64. 830722 64. 897803 1. 5 426. 40818 473. 55979 474. 83402 478. 51588 479. 25919 2. 0 3029. 3279 3484. 1608 3496. 6702 3532. 8789 3540. 2001

8. EDO’s 8. 2. 1 Método de Euler Aprimorado v v O Método de Euler Aprimorado fornece resultados muito melhores do que aqueles de Euler Direto e Inverso. O Método de Euler Aprimorado Adaptativo fornece melhores resultados através da variação no tamanho dos passos. Neste procedimento, variando o tamanho dos passos, mantemos constante o erro de truncamento local da aproximação