7 INVERSE FUNCTIONS INVERSE FUNCTIONS 7 4 General















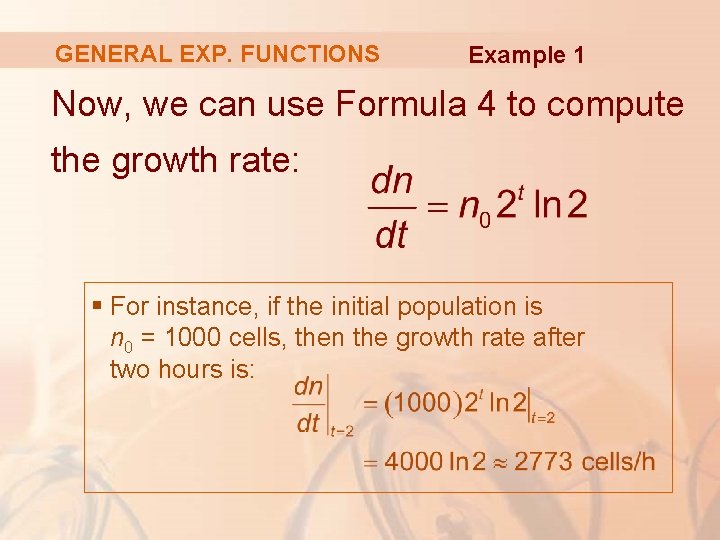







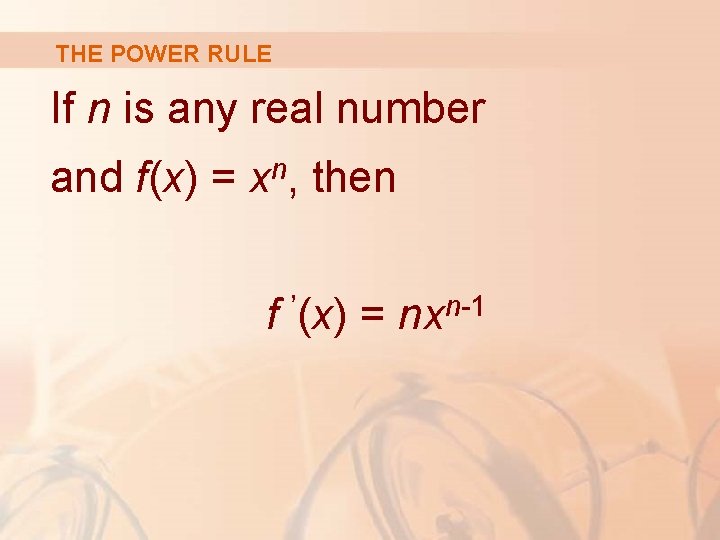










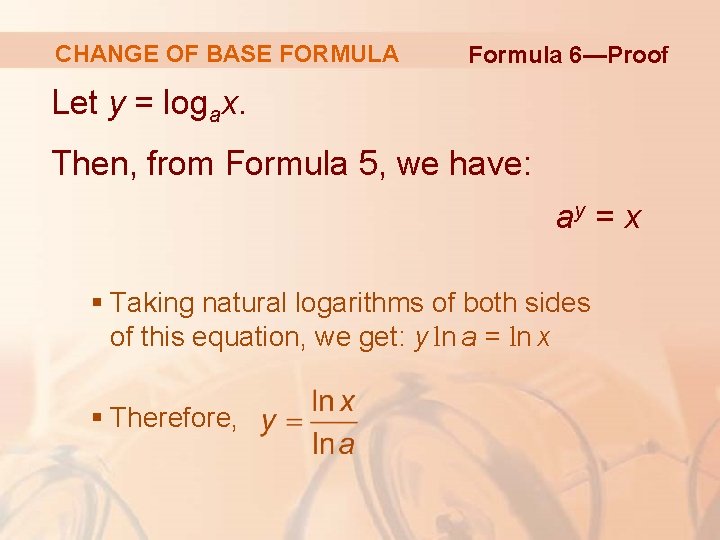



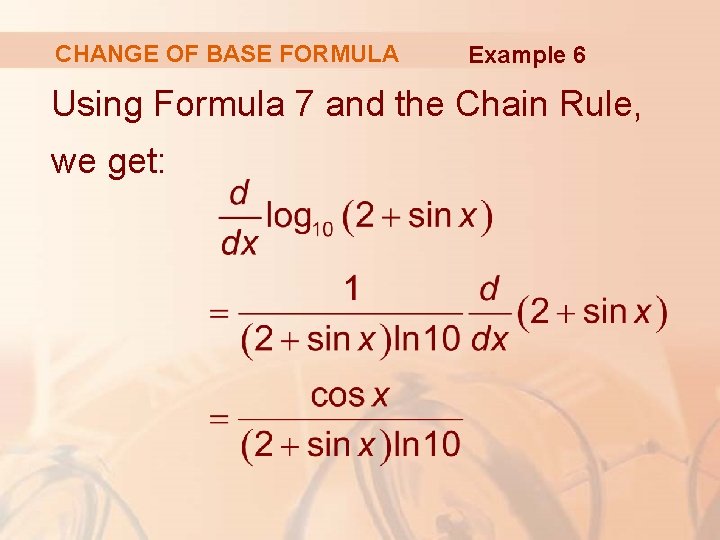




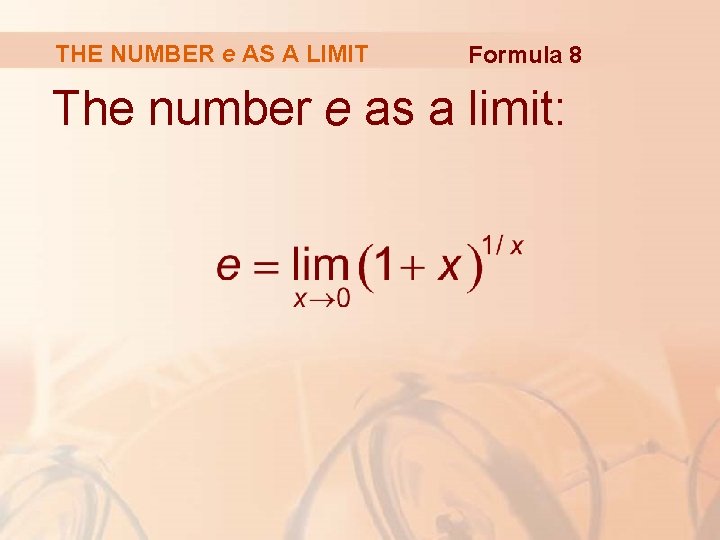
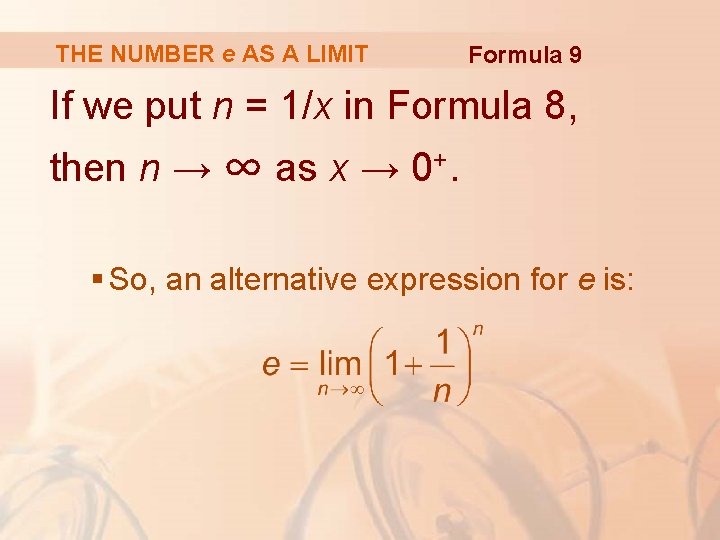
- Slides: 56

7 INVERSE FUNCTIONS

INVERSE FUNCTIONS 7. 4* General Logarithmic and Exponential Functions In this section, we: Use the natural exponential and logarithmic functions to study exponential and logarithmic functions with base a > 0.

GENERAL EXPONENTIAL FUNCTIONS If a > 0 and r is any rational number, then, by Equations 4 and 7 in Section 7. 3*, ar = (eln a)r = er ln a

GENERAL EXP. FUNCTIONS Definition 1 Thus, even for irrational numbers x, we define: ax = ex ln a § Thus, for instance,

GENERAL EXP. FUNCTIONS The function f(x) = ax is called the exponential function with base a. § Notice that ax is positive for all x because ex is positive for all x.

GENERAL EXP. FUNCTIONS Definition 1 allows us to extend one of the laws of logarithms. § We know that ln(ar) = r ln a when r is rational. § However, if we now let r be any real number we have, from Definition 1, ln ar = ln(er ln a) = r ln a

GENERAL EXP. FUNCTIONS Hence, we have: ln ar = r ln a for any real number r. Equation 2

GENERAL EXP. FUNCTIONS The general laws of exponents follow from Definition 1 together with the laws of exponents for ex.

LAWS OF EXPONENTS Laws 3 If x and y are real numbers and a, b > 0, then 1. ax+y = axay 2. ax-y = ax/ay 3. (ax)y = axy 4. (ab)x = axbx

LAW 1 OF EXPONENTS Proof Using Definition 1 and the laws of exponents for ex, we have:

LAW 3 OF EXPONENTS Proof Using Equation 2, we obtain: § The remaining proofs are left as exercises.

GENERAL EXP. FUNCTIONS Formula 4 The differentiation formula for exponential functions is also a consequence of Definition 1:

GENERAL EXP. FUNCTIONS Formula 4—Proof

GENERAL EXP. FUNCTIONS Notice that, if a = e, then ln e = 1 and Formula 4 simplifies to a formula we already know: (d/dx) ex = ex § In fact, the reason the natural exponential function is used more often than other exponential functions is that its differentiation formula is simpler.

GENERAL EXP. FUNCTIONS Example 1 In Example 6 in Section 3. 7, we considered a population of bacteria cells in a homogeneous nutrient medium. § We showed that, if the population doubles every hour, then the population after t hours is: n = n 02 t where n 0 is the initial population.
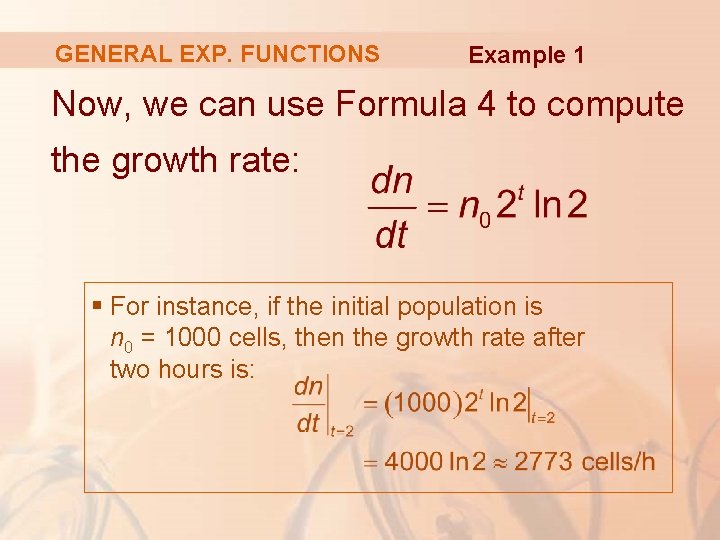
GENERAL EXP. FUNCTIONS Example 1 Now, we can use Formula 4 to compute the growth rate: § For instance, if the initial population is n 0 = 1000 cells, then the growth rate after two hours is:

GENERAL EXP. FUNCTIONS Example 2 Combining Formula 4 with the Chain Rule, we have:

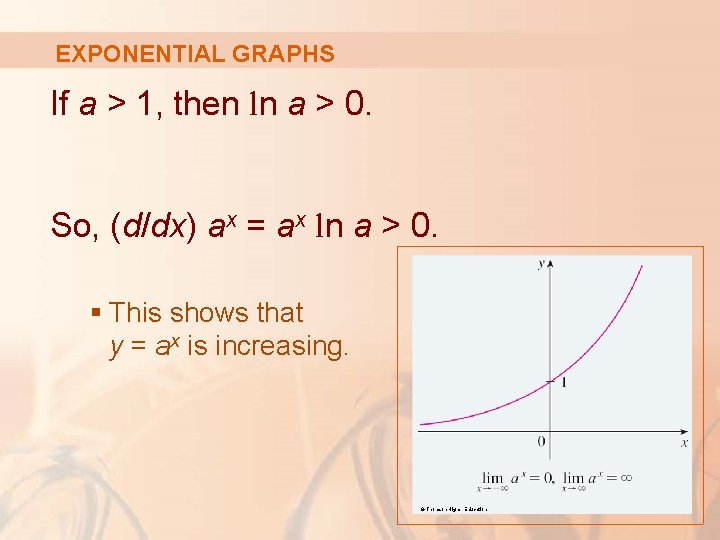
EXPONENTIAL GRAPHS If a > 1, then ln a > 0. So, (d/dx) ax = ax ln a > 0. § This shows that y = ax is increasing. © Thomson Higher Education

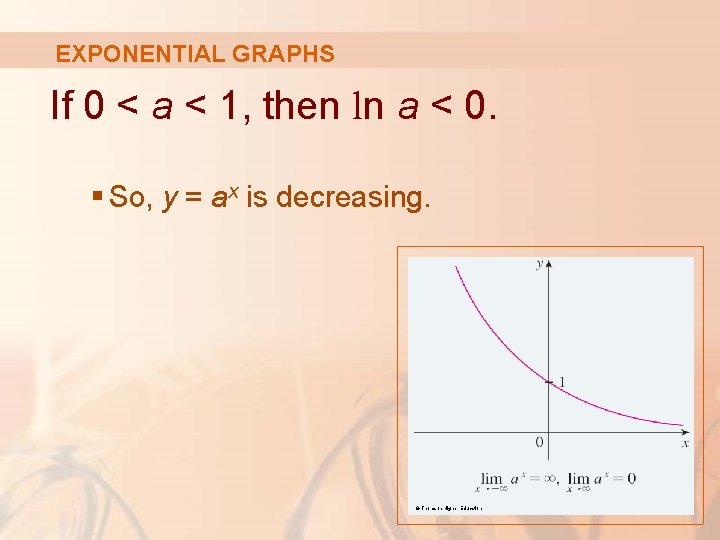
EXPONENTIAL GRAPHS If 0 < a < 1, then ln a < 0. § So, y = ax is decreasing. © Thomson Higher Education

EXPONENTIAL GRAPHS Notice from this figure that, as the base a gets larger, the exponential function grows more rapidly (for x > 0). © Thomson Higher Education

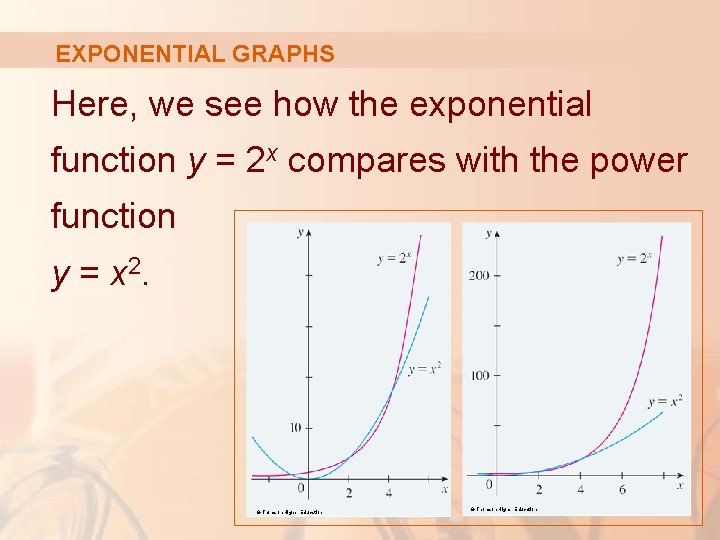
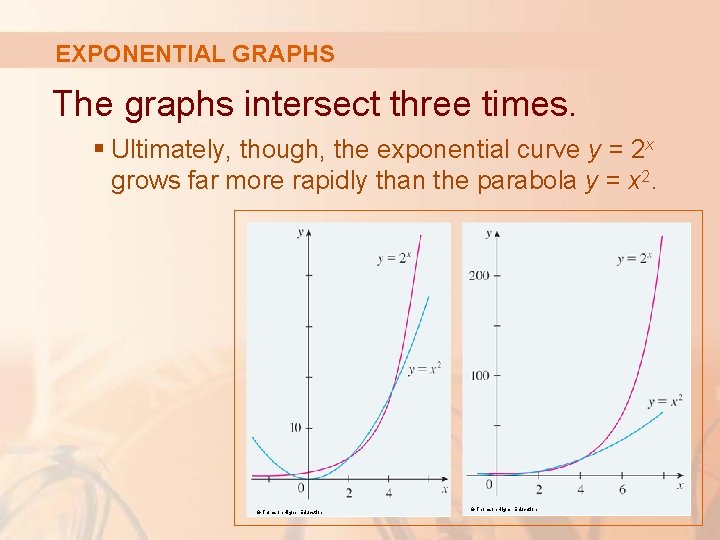
EXPONENTIAL GRAPHS Here, we see how the exponential function y = 2 x compares with the power function y = x 2. © Thomson Higher Education

EXPONENTIAL GRAPHS The graphs intersect three times. § Ultimately, though, the exponential curve y = 2 x grows far more rapidly than the parabola y = x 2. © Thomson Higher Education

EXPONENTIAL GRAPHS In Section 7. 5, we will show exponential functions occur in the description of population growth and radioactive decay. § Let’s look at human population growth.

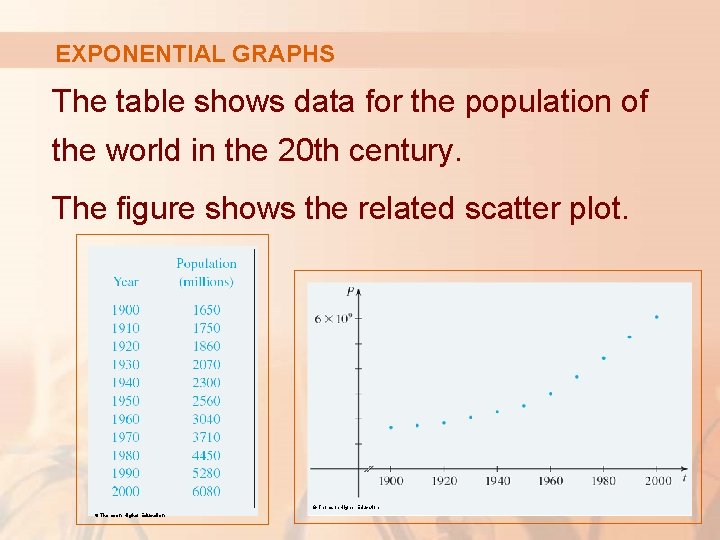
EXPONENTIAL GRAPHS The table shows data for the population of the world in the 20 th century. The figure shows the related scatter plot. © Thomson Higher Education

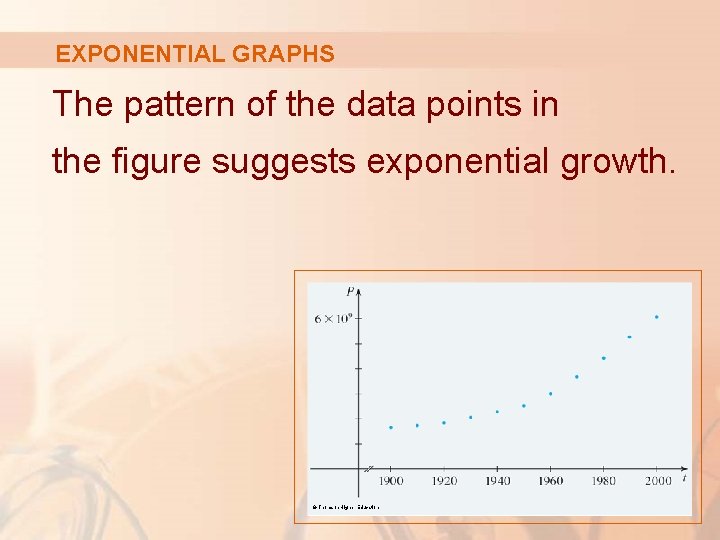
EXPONENTIAL GRAPHS The pattern of the data points in the figure suggests exponential growth. © Thomson Higher Education

EXPONENTIAL GRAPHS Hence, we use a graphing calculator with exponential regression capability to apply the method of least squares and obtain the exponential model P = (0. 008079266). (1. 013731)t

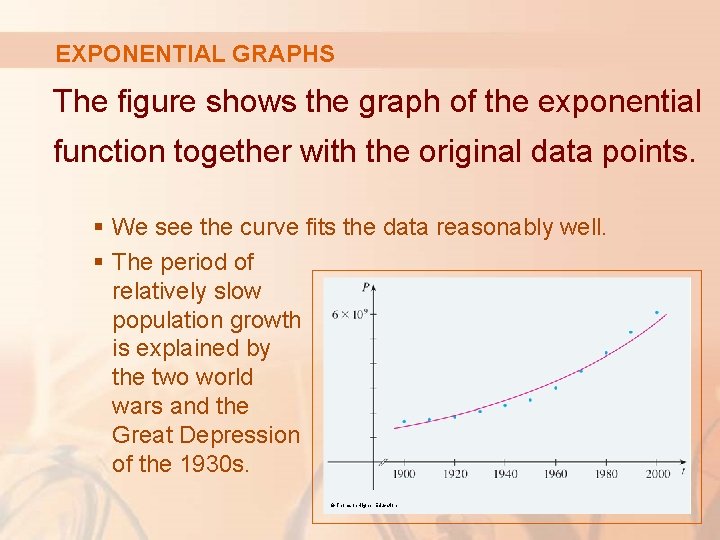
EXPONENTIAL GRAPHS The figure shows the graph of the exponential function together with the original data points. § We see the curve fits the data reasonably well. § The period of relatively slow population growth is explained by the two world wars and the Great Depression of the 1930 s. © Thomson Higher Education

EXPONENTIAL INTEGRALS The integration formula that follows from Formula 4 is:

EXPONENTIAL INTEGRALS Example 3

THE POWER RULE VS. THE EXPONENTIAL RULE Now that we have defined arbitrary powers of numbers, we are in a position to prove the general version of the Power Rule—as promised in Section 3. 3
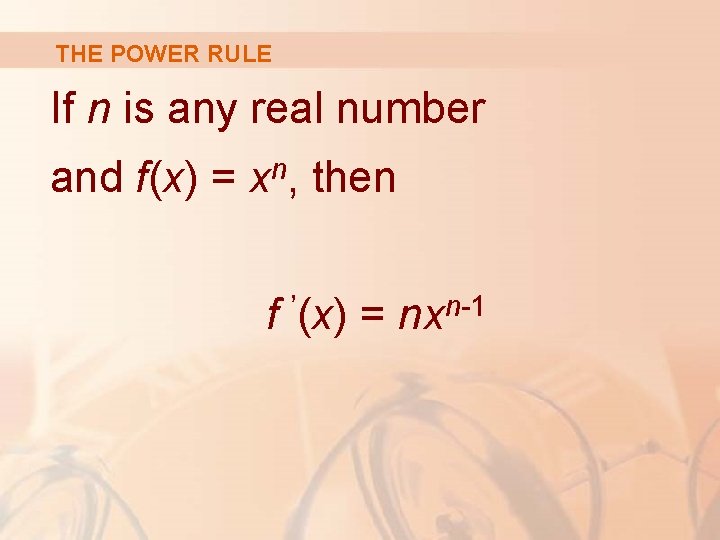
THE POWER RULE If n is any real number and f(x) = xn, then f ’(x) = n-1 nx

THE POWER RULE Proof Let y = xn and use logarithmic differentiation: ln | y | = ln | x |n = n ln | x | § Therefore, § Hence, x≠ 0

POWER RULE VS. EXP. RULE Note You should distinguish carefully between: § The Power Rule [(d/dx) xn = nxn-1], where the base is variable and the exponent is constant. § The rule for differentiating exponential functions [(d/dx) ax = ax ln a], where the base is constant and the exponent is variable.

THE POWER RULE—CASES In general, there are four cases for exponents and bases:

THE POWER RULE E. g. 4—Solution 1 Differentiate: § Using logarithmic differentiation, we have:

THE POWER RULE E. g. 4—Solution 2 Another method is to write

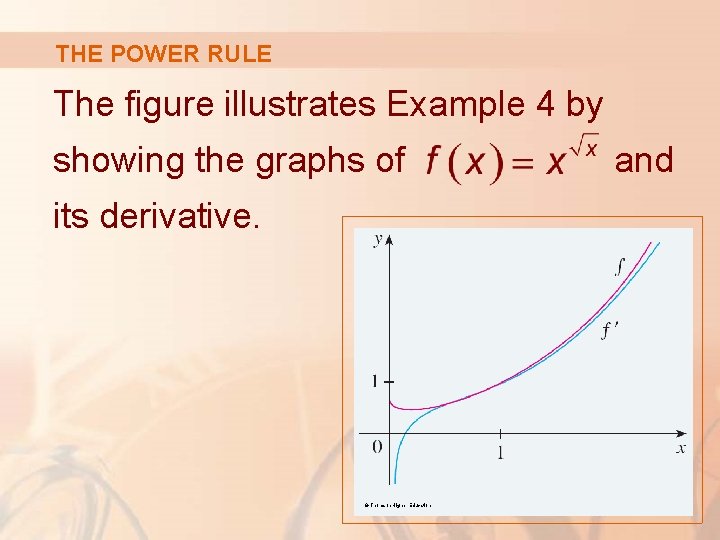
THE POWER RULE The figure illustrates Example 4 by showing the graphs of its derivative. © Thomson Higher Education and

GENERAL LOG. FUNCTIONS If a > 0 and a ≠ 1, then f(x) = ax is a one-to-one function. § Its inverse function is called the logarithmic function with base a. § It is denoted by loga.

GENERAL LOG. FUNCTIONS Formula 5 Thus, loga x = y ay = x § In particular, we see that: logex = ln x

GENERAL LOG. FUNCTIONS The cancellation equations for the inverse functions logax and ax are:

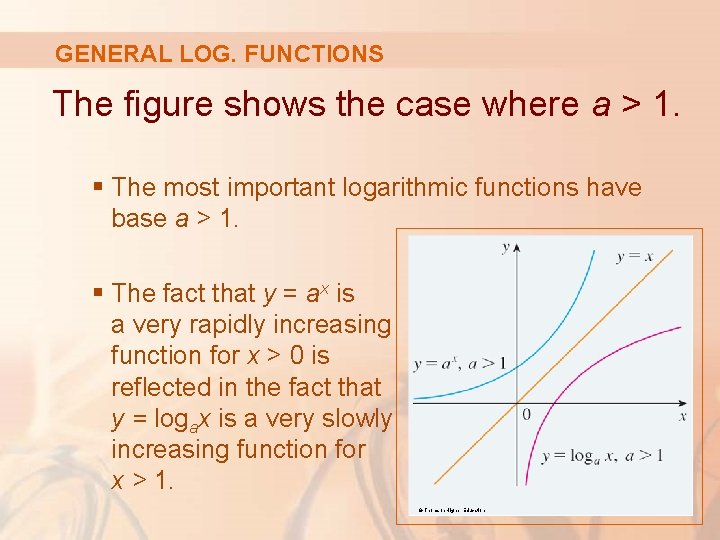
GENERAL LOG. FUNCTIONS The figure shows the case where a > 1. § The most important logarithmic functions have base a > 1. § The fact that y = ax is a very rapidly increasing function for x > 0 is reflected in the fact that y = logax is a very slowly increasing function for x > 1. © Thomson Higher Education

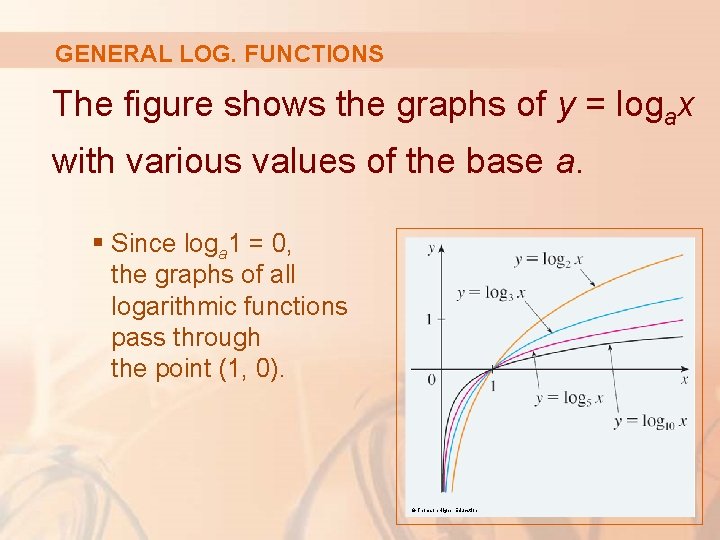
GENERAL LOG. FUNCTIONS The figure shows the graphs of y = logax with various values of the base a. § Since loga 1 = 0, the graphs of all logarithmic functions pass through the point (1, 0). © Thomson Higher Education

GENERAL LOG. FUNCTIONS The laws of logarithms are similar to those for the natural logarithm. § They can be deduced from the laws of exponents. § See Exercise 65.

CHANGE OF BASE FORMULA Formula 6 This formula shows that logarithms with any base can be expressed in terms of the natural logarithm. § For any positive number a (a ≠ 1), we have:
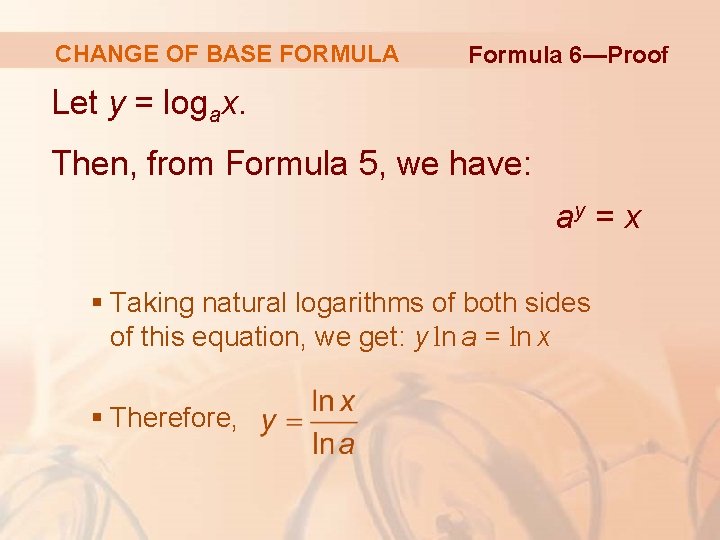
CHANGE OF BASE FORMULA Formula 6—Proof Let y = logax. Then, from Formula 5, we have: ay = x § Taking natural logarithms of both sides of this equation, we get: y ln a = ln x § Therefore,

CHANGE OF BASE FORMULA Scientific calculators have a key for natural logarithms. So, Formula 6 enables us to: § Use a calculator to compute a logarithm with any base (as shown in the following example). § Graph any logarithmic function on a graphing calculator or computer (as in Exercises 14 -16).

CHANGE OF BASE FORMULA Example 5 Evaluate log 85 correct to six decimal places. § Formula 6 gives:

CHANGE OF BASE FORMULA Formula 7 Formula 6 enables us to differentiate any logarithmic function. § Since ln a is a constant, we can differentiate as follows:
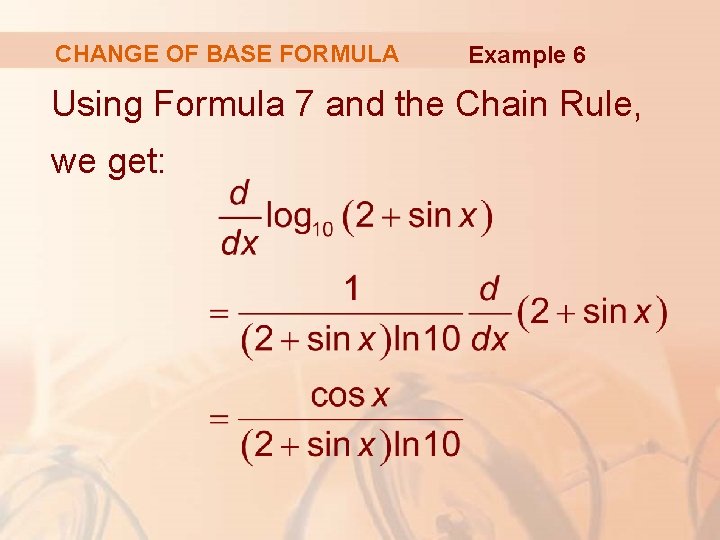
CHANGE OF BASE FORMULA Example 6 Using Formula 7 and the Chain Rule, we get:

CHANGE OF BASE FORMULA From Formula 7, we see one of the main reasons that natural logarithms (logarithms with base e) are used in calculus: § The differentiation formula is simplest when a = e because ln e = 1.

THE NUMBER e AS A LIMIT We have shown that, if f(x) = ln x, then f’(x) = 1/x. Thus, f’(1) = 1. § We now use this fact to express the number e as a limit.

THE NUMBER e AS A LIMIT From the definition of a derivative as a limit, we have:

THE NUMBER e AS A LIMIT Since f’(1) = 1, we have: § Then, by Theorem 8 in Section 2. 5 and the continuity of the exponential function, we have:
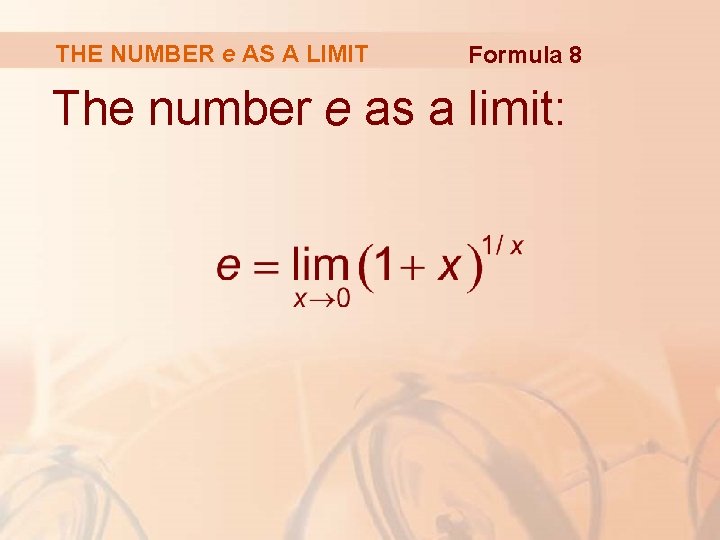
THE NUMBER e AS A LIMIT Formula 8 The number e as a limit:

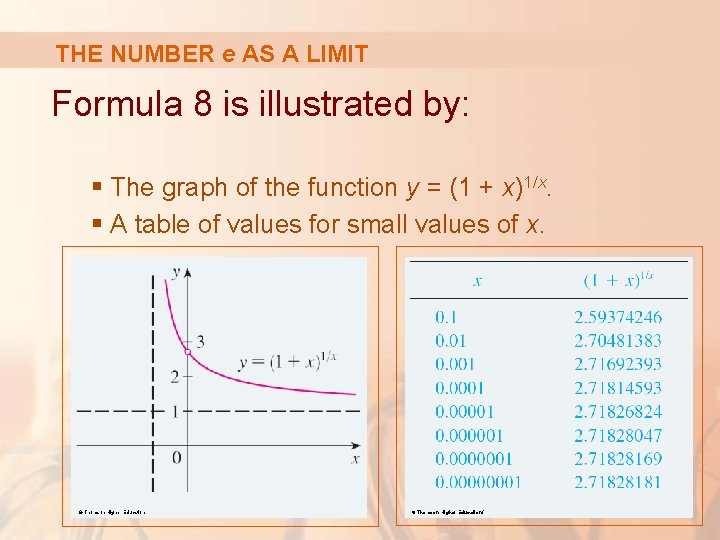
THE NUMBER e AS A LIMIT Formula 8 is illustrated by: § The graph of the function y = (1 + x)1/x. § A table of values for small values of x. © Thomson Higher Education/
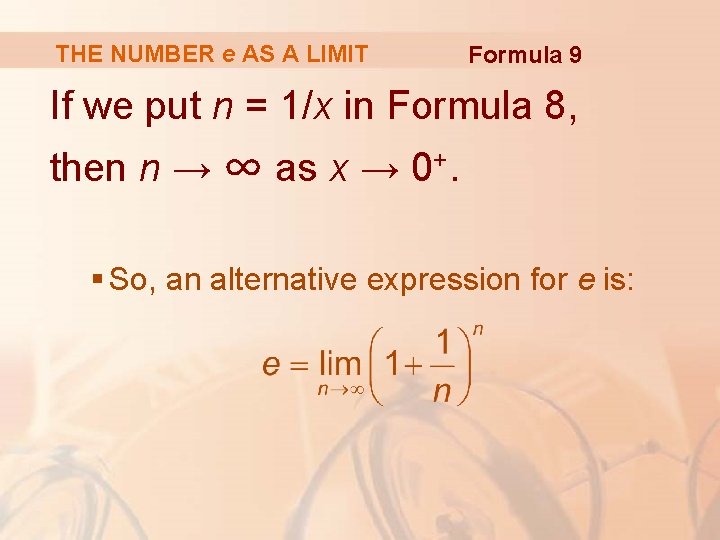
THE NUMBER e AS A LIMIT Formula 9 If we put n = 1/x in Formula 8, then n → ∞ as x → 0+. § So, an alternative expression for e is:
 Diferencia entre gran plano general y plano general
Diferencia entre gran plano general y plano general Where did general lee surrender to general grant?
Where did general lee surrender to general grant? 6 inverse trig functions
6 inverse trig functions Inverse trig table
Inverse trig table Domain of the inverse cosine function
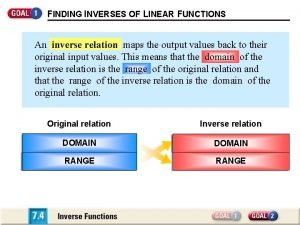
Domain of the inverse cosine function Inverse relations and functions
Inverse relations and functions Integration of inverse hyperbolic functions
Integration of inverse hyperbolic functions Inverse of linear functions
Inverse of linear functions Finding inverse of exponential functions
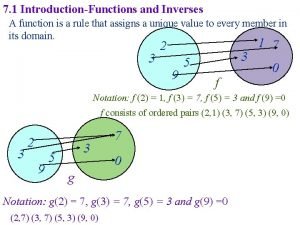
Finding inverse of exponential functions How to find the inverse of a function
How to find the inverse of a function Define inverse of a function with an arrow diagram
Define inverse of a function with an arrow diagram Derivative of inverse function
Derivative of inverse function Inverse trig function derivatives
Inverse trig function derivatives Integration of inverse trigonometric functions
Integration of inverse trigonometric functions Hyperbolic functions derivatives
Hyperbolic functions derivatives Inverse functions notes
Inverse functions notes Hyperbolic functions derivatives
Hyperbolic functions derivatives Inverse circular functions
Inverse circular functions Inverse variation graph calculator
Inverse variation graph calculator Integral of logarithmic functions
Integral of logarithmic functions Inverse functions and relations
Inverse functions and relations Real life application of inverse function
Real life application of inverse function Composite and inverse functions
Composite and inverse functions Lesson 1-4 inverses of functions
Lesson 1-4 inverses of functions Rational parent function table
Rational parent function table Implicit differentiation with inverse trig functions
Implicit differentiation with inverse trig functions Evaluating inverse trig functions without a calculator
Evaluating inverse trig functions without a calculator Inverse trig ratios and finding missing angles
Inverse trig ratios and finding missing angles Define inverse laplace transform
Define inverse laplace transform Proving inverse functions using composition
Proving inverse functions using composition Reverse exponential graph
Reverse exponential graph Inverse of a rational function
Inverse of a rational function 1-7 inverse relations and functions
1-7 inverse relations and functions 4-7 inverse linear functions
4-7 inverse linear functions 1-7 inverse relations and functions
1-7 inverse relations and functions Inverse functions linear discrete
Inverse functions linear discrete Inverse of exponential function
Inverse of exponential function Inverse function graph examples
Inverse function graph examples Inverse functions linear discrete
Inverse functions linear discrete What quadrants can inverse cosine be in
What quadrants can inverse cosine be in Inverse vs reciprocal trig functions
Inverse vs reciprocal trig functions Summary of inverse trigonometric functions
Summary of inverse trigonometric functions Tan inverse x
Tan inverse x How to find inverse of a function
How to find inverse of a function Derivative of the inverse function
Derivative of the inverse function Inverse trig derivatives
Inverse trig derivatives Trig ratios of general angles
Trig ratios of general angles Bessel differential equation example
Bessel differential equation example Direct motion specification is
Direct motion specification is Functions of the auditor general in zambia
Functions of the auditor general in zambia Quadratic functions general form
Quadratic functions general form Steps for graphing rational functions
Steps for graphing rational functions Absolute value as a piecewise function
Absolute value as a piecewise function Evaluating functions
Evaluating functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Proportion graphs
Proportion graphs Inverse of log function
Inverse of log function