7 4 Graphing Quadratic Functions Preview Warm Up

7 -4 Graphing Quadratic Functions Preview Warm Up California Standards Lesson Presentation Holt CA Course 1

7 -4 Graphing Quadratic Functions Warm Up For each function, find the value of y for x = 0, x = 4, and x = – 5. 1. y = 6 x – 3, 21, – 33 2. y = 3. 8 x – 12, 3. 2, – 31 3. y = 1. 6 x + 5. 9, 12. 3, – 2. 1 Holt CA Course 1

7 -4 Graphing Quadratic Functions California Standards AF 3. 1 Graph functions of the form y = nx 2 and y = nx 3 and use in solving problems. Holt CA Course 1

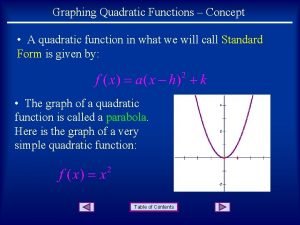
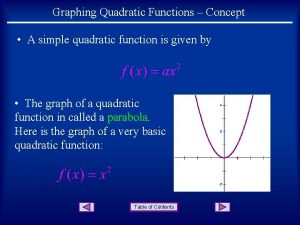
7 -4 Graphing Quadratic Functions Vocabulary quadratic function parabola Holt CA Course 1

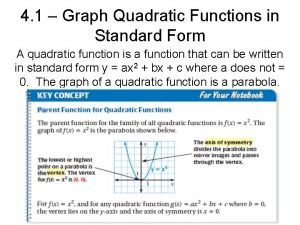
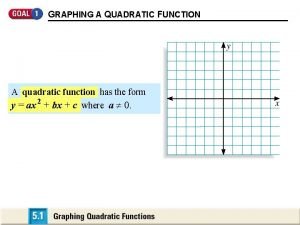
7 -4 Graphing Quadratic Functions A quadratic function is a function in which the greatest power of the variable is 2. The most basic quadratic function is y = nx 2 where n ≠ 0. The graphs of all quadratic functions have the same basic shape, called a parabola. Holt CA Course 1

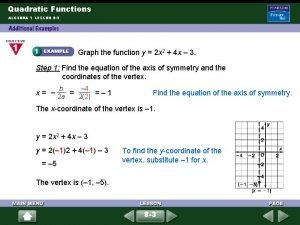
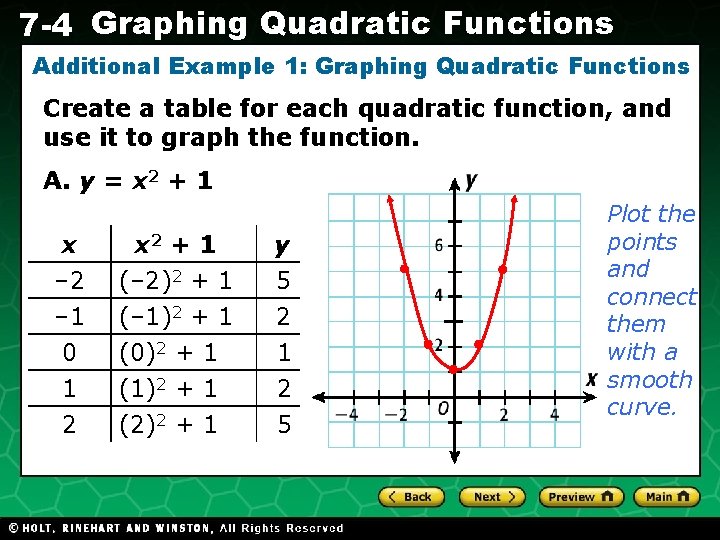
7 -4 Graphing Quadratic Functions Additional Example 1: Graphing Quadratic Functions Create a table for each quadratic function, and use it to graph the function. A. y = x 2 + 1 x – 2 – 1 0 1 2 x 2 + 1 y (– 2)2 + 1 (– 1)2 + 1 (0)2 + 1 (1)2 + 1 (2)2 + 1 5 2 1 2 5 Holt CA Course 1 Plot the points and connect them with a smooth curve.

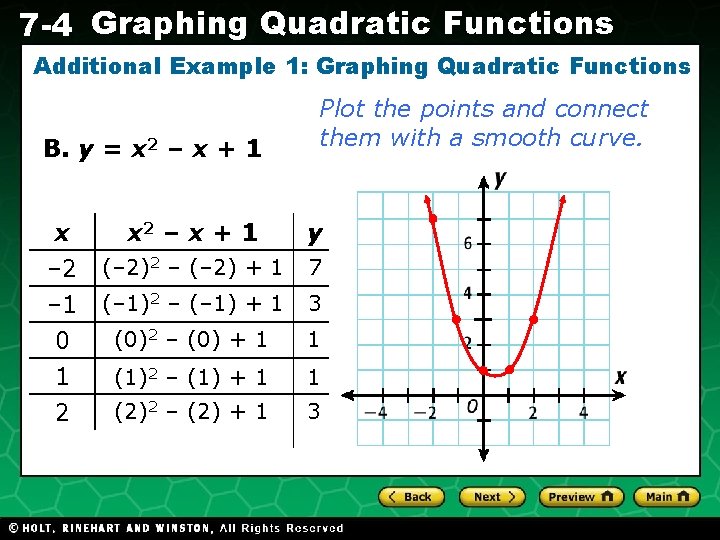
7 -4 Graphing Quadratic Functions Additional Example 1: Graphing Quadratic Functions B. y = x 2 – x + 1 x – 2 – 1 0 1 2 Plot the points and connect them with a smooth curve. x 2 – x + 1 y (– 2)2 – (– 2) + 1 7 (– 1)2 – (– 1) + 1 3 (0)2 – (0) + 1 1 (1)2 – (1) + 1 1 (2)2 – (2) + 1 3 Holt CA Course 1

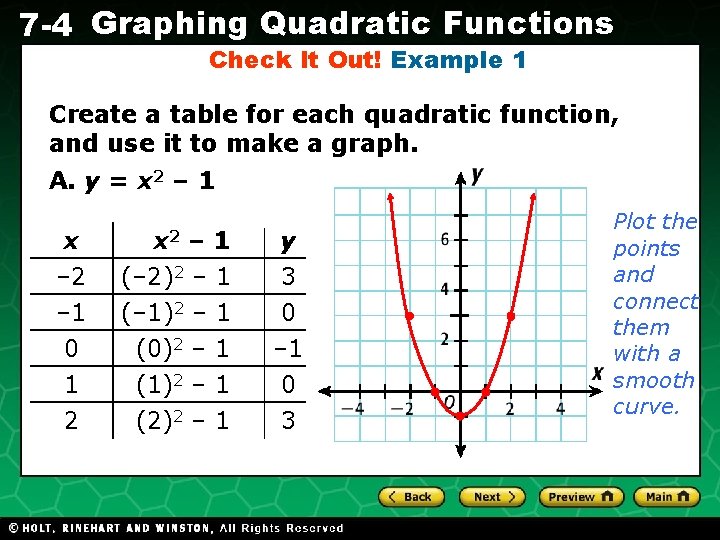
7 -4 Graphing Quadratic Functions Check It Out! Example 1 Create a table for each quadratic function, and use it to make a graph. A. y = x 2 – 1 x – 2 – 1 0 1 2 x 2 (– 2)2 (– 1)2 (0)2 (1)2 (2)2 Holt CA Course 1 – – – 1 1 1 y 3 0 – 1 0 3 Plot the points and connect them with a smooth curve.

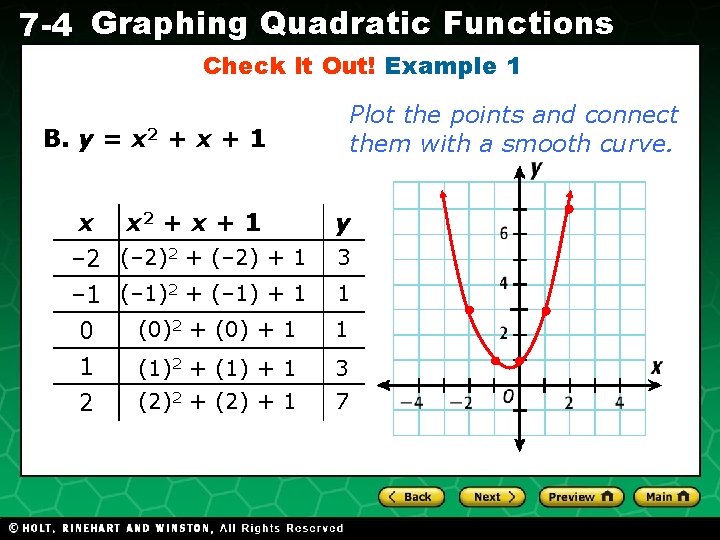
7 -4 Graphing Quadratic Functions Check It Out! Example 1 Plot the points and connect them with a smooth curve. B. y = x 2 + x + 1 x x 2 + x + 1 – 2 (– 2)2 + (– 2) + 1 – 1 (– 1)2 + (– 1) + 1 (0)2 + (0) + 1 0 1 2 y 3 1 1 (1)2 + (1) + 1 3 (2)2 + (2) + 1 7 Holt CA Course 1

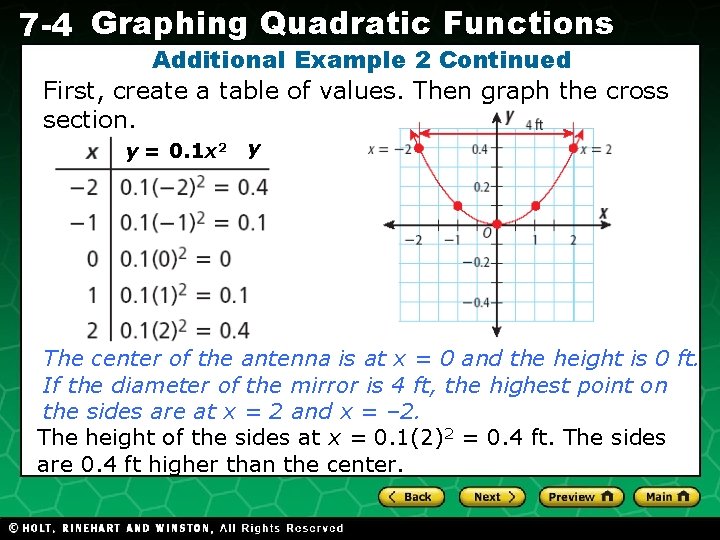
7 -4 Graphing Quadratic Functions Additional Example 2: Application A reflecting surface of a television antenna was formed by rotating the parabola y = 0. 1 x 2 about its axis of symmetry. If the antenna has a diameter of 4 feet, about how much higher are the sides than the center? Holt CA Course 1

7 -4 Graphing Quadratic Functions Additional Example 2 Continued First, create a table of values. Then graph the cross section. y = 0. 1 x 2 y The center of the antenna is at x = 0 and the height is 0 ft. If the diameter of the mirror is 4 ft, the highest point on the sides are at x = 2 and x = – 2. The height of the sides at x = 0. 1(2)2 = 0. 4 ft. The sides are 0. 4 ft higher than the center. Holt CA Course 1

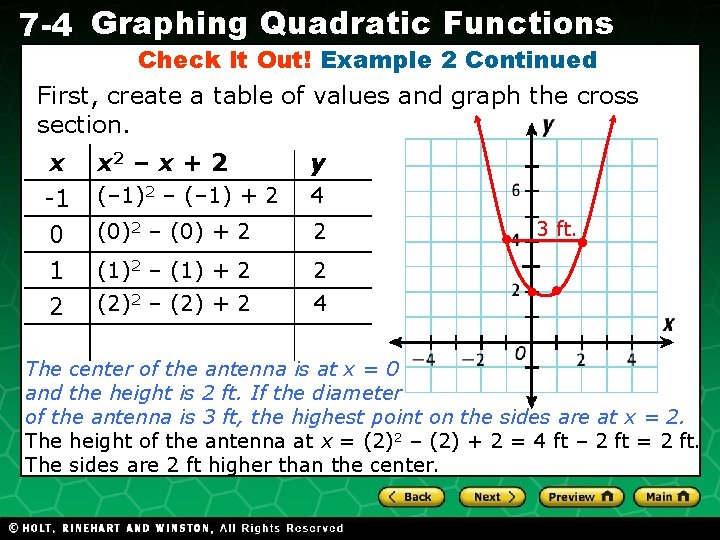
7 -4 Graphing Quadratic Functions Check It Out! Example 2 A reflecting surface of a radio antenna was formed by rotating the parabola y = x 2 – x + 2 about its axis of symmetry. If the antenna has a diameter of 3 feet, about how much higher are the sides than the center? Holt CA Course 1

7 -4 Graphing Quadratic Functions Check It Out! Example 2 Continued First, create a table of values and graph the cross section. x -1 0 1 x 2 – x + 2 y (– 1)2 – (– 1) + 2 4 (0)2 – (0) + 2 2 (1)2 – (1) + 2 2 2 (2)2 – (2) + 2 4 3 ft. The center of the antenna is at x = 0 and the height is 2 ft. If the diameter of the antenna is 3 ft, the highest point on the sides are at x = 2. The height of the antenna at x = (2)2 – (2) + 2 = 4 ft – 2 ft = 2 ft. The sides are 2 ft higher than the center. Holt CA Course 1

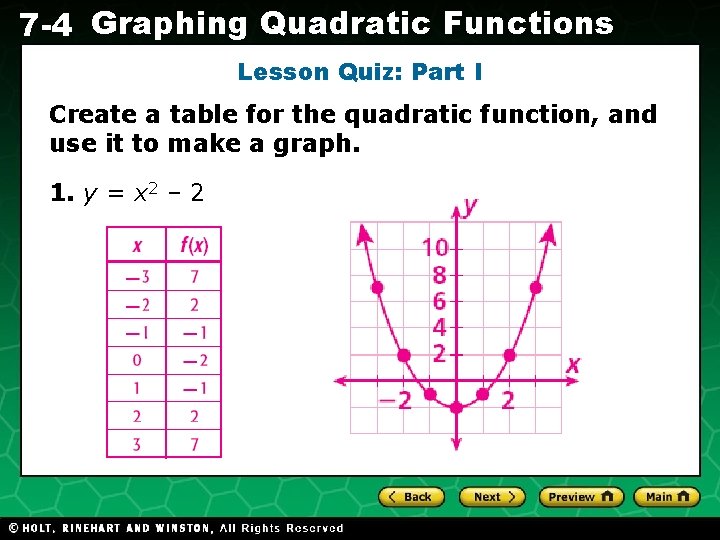
7 -4 Graphing Quadratic Functions Lesson Quiz: Part I Create a table for the quadratic function, and use it to make a graph. 1. y = x 2 – 2 Holt CA Course 1

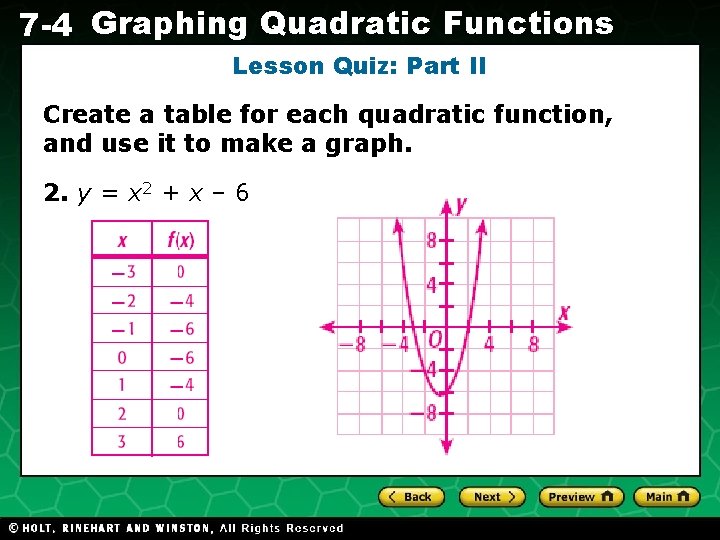
7 -4 Graphing Quadratic Functions Lesson Quiz: Part II Create a table for each quadratic function, and use it to make a graph. 2. y = x 2 + x – 6 Holt CA Course 1

7 -4 Graphing Quadratic Functions Lesson Quiz: Part III 3. The function y = 40 t – 5 t 2 gives the height of an arrow in meters t seconds after it is shot upward. What is the height of the arrow after 5 seconds? 75 m Holt CA Course 1