Section 4 1 Notes Graphing Quadratic Functions Quadratic

Section 4. 1 Notes: Graphing Quadratic Functions

Quadratic Function: Characteristics *Greatest exponent is 2. *Its graph is called a parabola. f(x) = ax 2 + bx + c, where a ≠ 0 Quadratic Term Linear Term Constant Term

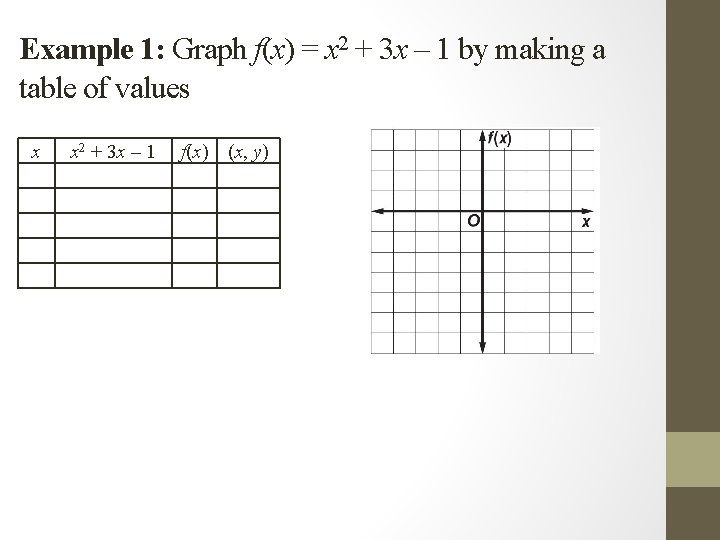
Example 1: Graph f(x) = x 2 + 3 x – 1 by making a table of values x x 2 + 3 x – 1 f(x) (x, y)

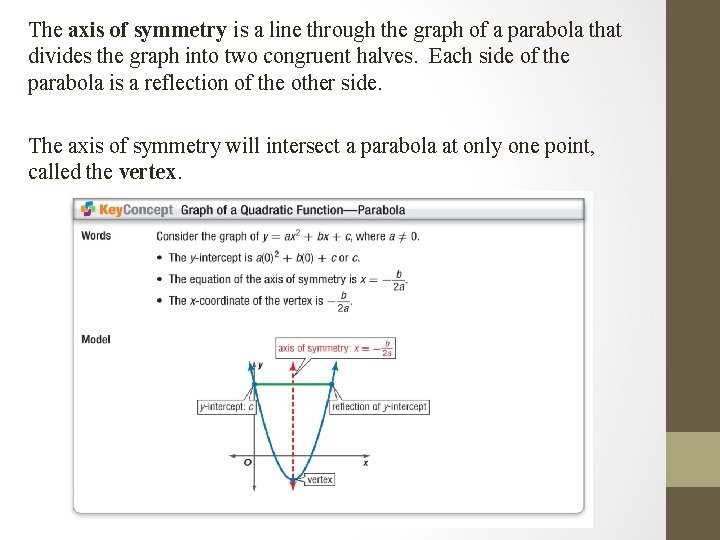
The axis of symmetry is a line through the graph of a parabola that divides the graph into two congruent halves. Each side of the parabola is a reflection of the other side. The axis of symmetry will intersect a parabola at only one point, called the vertex.

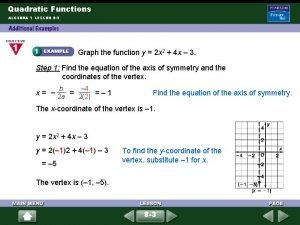
Example 2: a) Consider the quadratic function f(x) = 2 – 4 x + x 2. Find the yintercept, the equation of the axis of symmetry, and the x-coordinate of the vertex.

b) Make a table of values that includes the vertex. x 2 – 4 x + x 2 f(x) (x, y) c) Use the information from parts a and b to graph the function

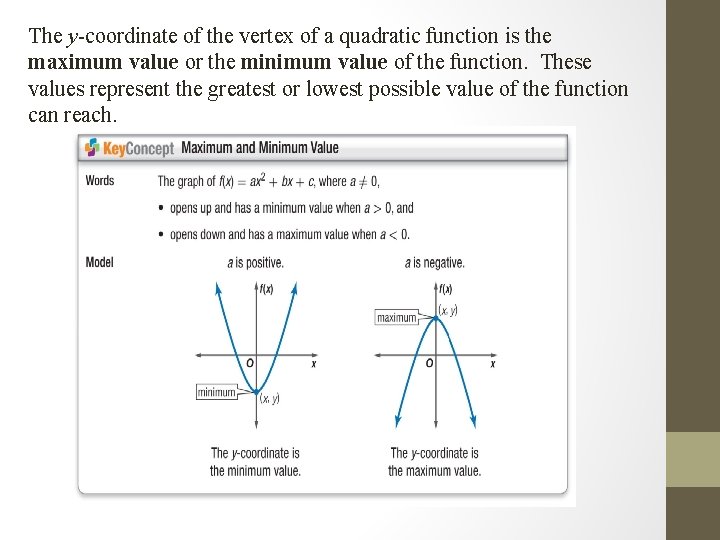
The y-coordinate of the vertex of a quadratic function is the maximum value or the minimum value of the function. These values represent the greatest or lowest possible value of the function can reach.

Domain and Range of Quadratics The domain of a quadratic function will always be all real numbers. The range will either be: • all real numbers less than or equal to the maximum • all real numbers greater than or equal to the minimum.

Example 3: Consider the function f(x) = –x 2 + 2 x + 3. a) Determine whether the function has a maximum or minimum value. b) State the maximum or minimum value of the function. c) State the domain and range of the function

Example 4: The path of a diver is approximated by feet in the figure shown and the equation given. What is the maximum height of the diver? Approximately how long did it take the diver to reach his maximum height?