68402 Structural Design of Buildings II 61420 Design

68402: Structural Design of Buildings II 61420: Design of Steel Structures 62323: Architectural Structures II Tension Member Design l l Monther Dwaikat Assistant Professor Department of Building Engineering An-Najah National University 68402 Slide # 1

Table of Contents l Typical Tension Members l Introductory Concepts l Design Strength l Effective and Net Areas l Staggered Bolted Connections l Block Shear l Design of Tension Members l Slenderness Requirements 68402 2

Tension Members l Applications l In bridge, roof and floor trusses, bracing systems, towers, and tie rods l Consist of angles, channels, tees, plates, W or S shapes, or combinations 68402 3

Typical Tension Members l Tension chord in a truss 68402 4

Typical Tension Members l Cables l Ties 68402 5

Tension Members l Commonly Used Sections: • W/H shapes • Square and Rectangular or round HSS • Tees and Double Tees • Angles and double angles • Channel sections • Cables 68402 6

Introductory Concepts l Stress: The stress in the column cross section can be calculated as f - assumed to be uniform over the entire cross-section. P - the magnitude of load A - the cross-sectional area normal to the load l The stress in a tension member is uniform throughout the cross section except: • • near the point of application of load at the cross section with holes for bolts or other discontinuities, etc. 68402 7

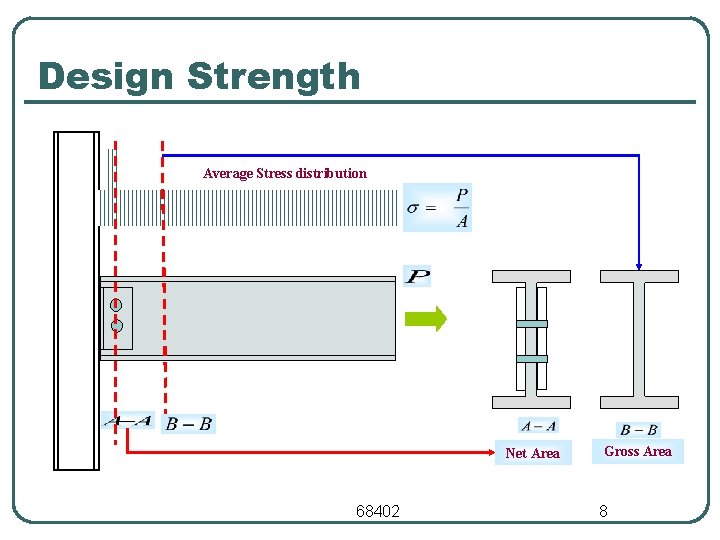
Design Strength Average Stress distribution Net Area 68402 Gross Area 8

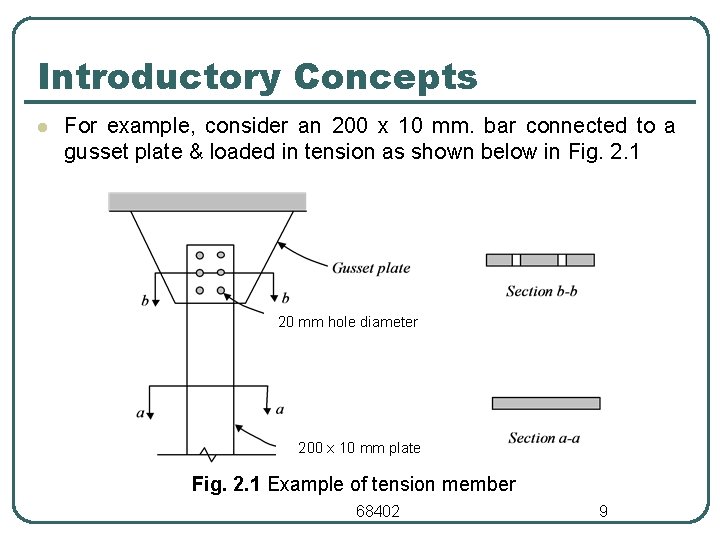
Introductory Concepts l For example, consider an 200 x 10 mm. bar connected to a gusset plate & loaded in tension as shown below in Fig. 2. 1 20 mm hole diameter 200 x 10 mm plate Fig. 2. 1 Example of tension member 68402 9

Introductory Concepts l Area of bar at section a – a = 200 x 10 = 2000 mm 2 l Area of bar at section b – b = (200 – 2 x 20 ) x 10 = 1600 mm 2 l Therefore, by definition the reduced area of section b – b will be subjected to higher stresses l However, the reduced area & therefore the higher stresses will be localized around section b – b. l The unreduced area of the member is called its gross area = Ag l The reduced area of the member is called its net area = An 68402 10

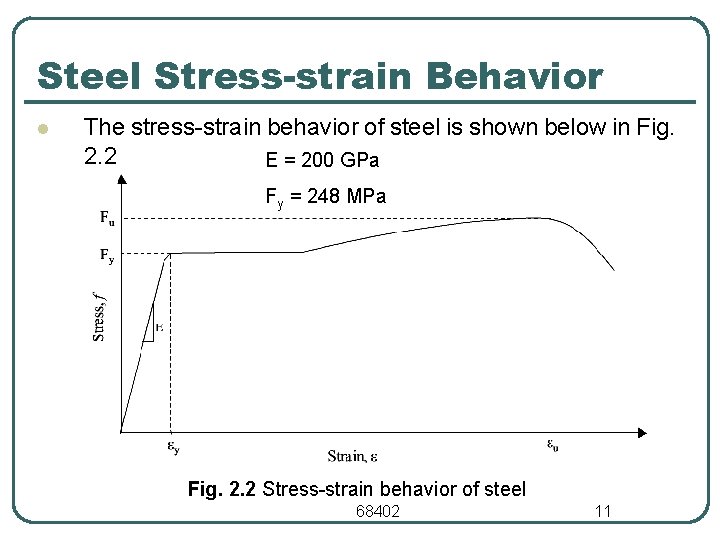
Steel Stress-strain Behavior l The stress strain behavior of steel is shown below in Fig. 2. 2 E = 200 GPa Fy = 248 MPa Fig. 2. 2 Stress strain behavior of steel 68402 11

Steel Stress-strain Behavior l In Fig. 2. 2: • • E the elastic modulus = 200 GPa. Fy the yield stress Fu the ultimate stress y is the yield strain u the ultimate strain Deformations are caused by the strain . Fig. 2. 2 indicates that the structural deflections will be small as long as the material is elastic (f < Fy) • Deformations due to the strain will be large after the steel reaches its yield stress Fy. 68402 12

Design Strength l We usually determine the strength “capacity” of any structural element based on possible scenarios of failure! l Possible failures of a tension member include • Yield of the element • Fracture of element l The stress of axially loaded elements can be determined as l The stress is therefore a function of the cross sectional area thus the presence of holes will change the stress. l Bolted connections reduce the area of the cross section. 68402 13

Design Strength l A tension member can fail by reaching one of two limit states: • • excessive deformation fracture l Excessive deformation can occur due to the yielding of the gross section (for example section a a from Fig. 2. 1) along the length of the member l Fracture of the net section can occur if the stress at the net section (for example section b b in Fig. 2. 1) reaches the ultimate stress Fu. l The objective of design is to prevent these failure before reaching the ultimate loads on the structure (Obvious). l This is also the load & resistance factor design approach for designing steel structures 68402 14

Load & Resistance Factor Design l The load & resistance factor design approach is recommended by AISC for designing steel structures. It can be understood as follows: • Step I. Determine the ultimate loads acting on the structure • The values of D, L, W, etc. are nominal loads (not maximum or ultimate) • During its design life, a structure can be subjected to some maximum or ultimate loads caused by combinations of D, L, or W loading. • The ultimate load on the structure can be calculated using factored load combinations. The most relevant of these load combinations are given below: 68402 15

Load & Resistance Factor Design • 1. 4 D • 1. 2 D + 1. 6 L + 0. 5 (Lr or S) • 1. 2 D + 1. 6 (Lr or S) + (0. 5 L or 0. 8 W) • 1. 2 D + 1. 6 W + 0. 5 L + 0. 5 (Lr or S) • 0. 9 D + 1. 6 W 68402 16

Load & Resistance Factor Design • Step III. Design the members • The failure (design) strength of the designed member must be greater than the corresponding design forces calculated in Step II: Rn - the calculated failure strength of the member - the resistance factor used to account for the reliability of the material behavior & equations for Rn Qi - the nominal load i - the load factor used to account for the variability in loading & to estimate the ultimate loading 68402 17

Design Strength of Tension Members l Yielding of the gross section will occur when the stress f reaches Fy. l Therefore, nominal yield strength = Pn = Ag Fy Factored yield strength = t Pn t = 0. 9 for tension yielding limit state l 68402 18

Design Strength of Tension Members l Facture of the net section will occur after the stress on the net section area reaches the ultimate stress Fu l Therefore, nominal fracture strength = Pn = Ae Fu l Where, Ae is the effective net area, which may be equal to the net area or smaller. l The topic of Ae will be addressed later. l Factored fracture strength = t Ae Fu where: t = 0. 75 for tension fracture limit state 68402 19

Net Area l We calculate the net area by deducting the width of the “bolts + some tolerance around the bolt” l Use a tolerance of 1. 6 mm above the diameter hole which is typically 1. 6 mm larger than the bolt diameter l Rule b t dbolt dhole 68402 20

Design Strength l l Tensile strength of a section is governed by two limit states: • • Yield of gross area (excessive deformation) Fracture of net area Thus the design strength is one of the following Load Effect YIELD FRACTURE l The difference in the factor for the two limit states represent the • • Seriousness of the fracture limit state The reliability index (probability of failure) assumed with each limit state 68402 21

Important Notes l Why is fracture (& not yielding) the relevant limit state at the net section? Yielding will occur first in the net section. However, the deformations induced by yielding will be localized around the net section. These localized deformations will not cause excessive deformations in the complete tension member. Hence, yielding at the net section will not be a failure limit state. l Why is the resistance factor ( t) smaller for fracture than for yielding? The smaller resistance factor fracture ( t = 0. 75 as compared to t = 0. 90 for yielding) reflects the more serious nature & consequences of reaching the fracture limit state. 68402 22

Important Notes l What is the design strength of the tension member? The design strength of the tension member will be the lesser value of the strength for the two limit states (gross section yielding & net section fracture). l Where are the Fy & Fu values for different steel materials? The yield & ultimate stress values for different steel materials are dependent on type of steel. 68402 23

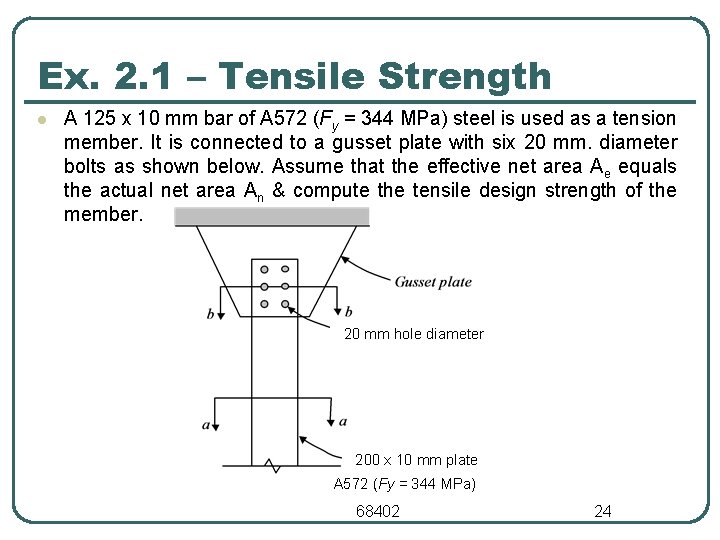
Ex. 2. 1 – Tensile Strength l A 125 x 10 mm bar of A 572 (Fy = 344 MPa) steel is used as a tension member. It is connected to a gusset plate with six 20 mm. diameter bolts as shown below. Assume that the effective net area Ae equals the actual net area An & compute the tensile design strength of the member. 20 mm hole diameter 200 x 10 mm plate A 572 (Fy = 344 MPa) 68402 24

Ex. 2. 1 – Tensile Strength l Gross section area = Ag = 125 x 10 = 1250 mm 2 l Net section area (An) l • • Bolt diameter = db = 20 mm. Nominal hole diameter = dh = 20 + 1. 6 = 21. 6 mm Hole diameter for calculating net area = 21. 6 + 1. 6 = 23. 2 mm Net section area = An = (125 – 2 x (23. 2)) x 10 = 786 mm 2 Gross yielding design strength = t Pn = t Fy Ag • Gross yielding design strength = 0. 9 x 344 x 1250/1000 = 387 k. N 68402 25

Ex. 2. 1 – Tensile Strength l l Fracture design strength = t Pn = t Fu Ae • • Assume Ae = An (only for this problem) Fracture design strength = 0. 75 x 448 x 786/1000 = 264 k. N Design strength of the member in tension = smaller of 264 k. N & 387 k. N • Therefore, design strength = 264 k. N (net section fracture controls). 68402 26

Effective Net Area l The connection has a significant influence on the performance of a tension member. A connection almost always weakens the member & a measure of its influence is called joint efficiency. l Joint efficiency is a function of: l • • • material ductility fastener spacing stress concentration at holes fabrication procedure shear lag. All factors contribute to reducing the effectiveness but shear lag is the most important. 68402 27

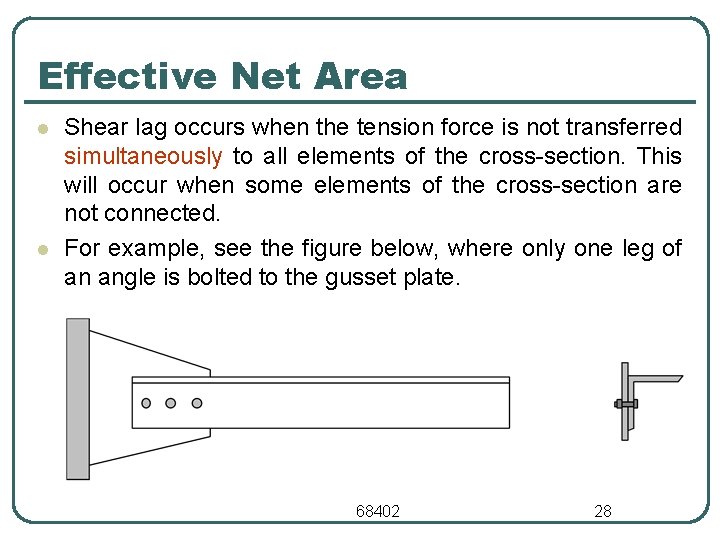
Effective Net Area l l Shear lag occurs when the tension force is not transferred simultaneously to all elements of the cross section. This will occur when some elements of the cross section are not connected. For example, see the figure below, where only one leg of an angle is bolted to the gusset plate. 68402 28

Effective Net Area l A consequence of this partial connection is that the connected element becomes overloaded & the unconnected part is not fully stressed. l Lengthening the connection region will reduce this effect l Research indicates that shear lag can be accounted for by using a reduced or effective net area Ae l Shear lag affects both bolted & welded connections. Therefore, the effective net area concept applied to both types of connections. • • For bolted connection, the effective net area is Ae = U An For welded connection, the effective net area is Ae = U Ag 68402 29

Effective Net Area l l l The way the tension member is connected affects its efficiency because of the “Shear Lag” phenomenon Shear lag occurs when the force is transmitted to the section through part of the section (not the whole section) To account for this stress concentration in stress, an area reduction factor “U” is used Bolted Connections Welded Connections Over stressed Under stressed 68402 30

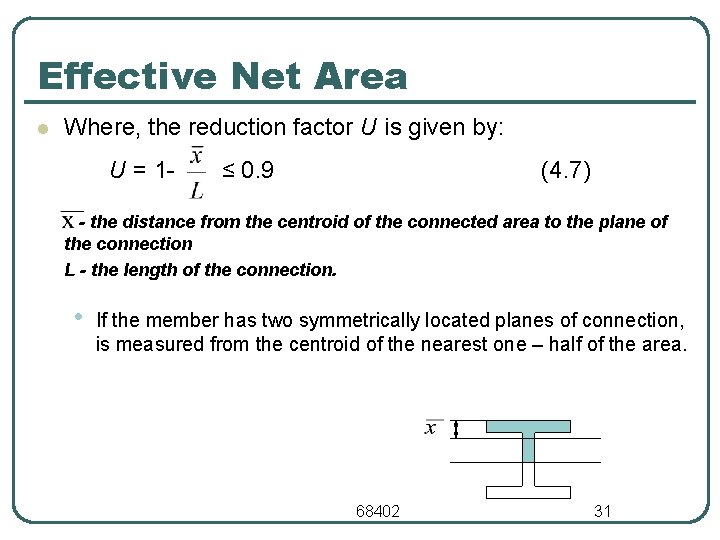
Effective Net Area l Where, the reduction factor U is given by: U = 1 ≤ 0. 9 (4. 7) - the distance from the centroid of the connected area to the plane of the connection L - the length of the connection. • If the member has two symmetrically located planes of connection, is measured from the centroid of the nearest one – half of the area. 68402 31

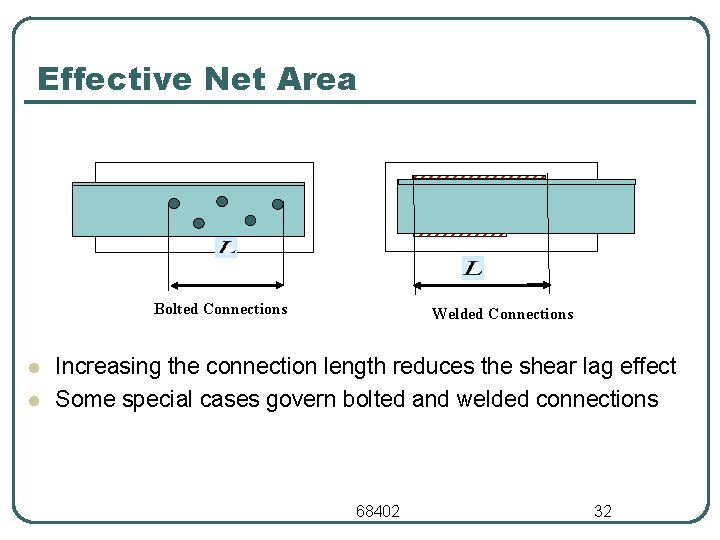
Effective Net Area Bolted Connections l l Welded Connections Increasing the connection length reduces the shear lag effect Some special cases govern bolted and welded connections 68402 32

Effective Net Area l The distance L is defined as the length of the connection in the direction of load. • For bolted connections, L is measured from the center of the bolt at one end to the center of the bolt at the other end. • For welded connections, it is measured from one end of the connection to other. • If there are weld segments of different length in the direction of load, L is the length of the longest segment. 68402 33

U for Bolted Connections OR l Two major groups of bolted connections • • Connections with at least three bolts per line • W, M and S shapes and T cut from them connected in flange with • All other shapes Connections with only two bolts per line 68402 34

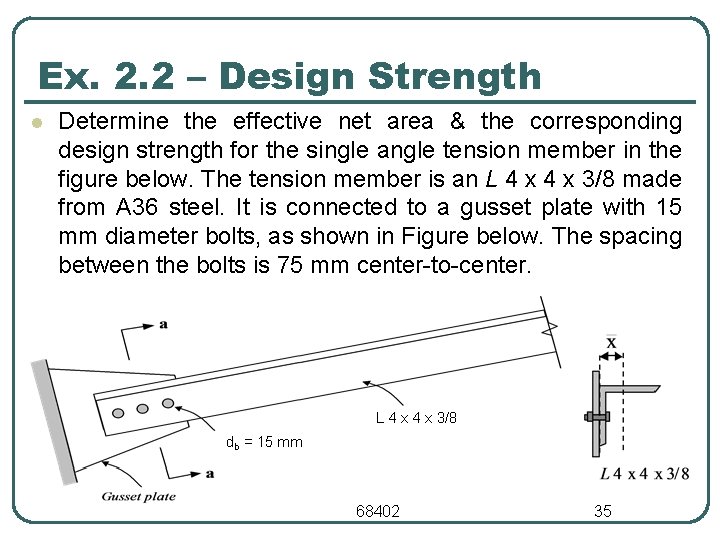
Ex. 2. 2 – Design Strength l Determine the effective net area & the corresponding design strength for the single angle tension member in the figure below. The tension member is an L 4 x 3/8 made from A 36 steel. It is connected to a gusset plate with 15 mm diameter bolts, as shown in Figure below. The spacing between the bolts is 75 mm center to center. L 4 x 3/8 db = 15 mm 68402 35

Ex. 2. 2 – Design Strength • • Gross area of angle = Ag = 1850 mm 2 • is the distance from the centroid of the area connected to the plane of connection • For this case is equal to the distance of centroid of the angle from the edge. • This value is given in the section property table. T = 9. 5 mm Net section area = An • Bolt diameter = 15 mm. • Hole diameter for calculating net area = 15 +3. 2 = 18. 2 mm. • Net section area = Ag – 18. 2 x 9. 5 = 1850 – 172. 9 = 1677. 1 mm 2 • = 28. 7 mm. 68402 36

Ex. 2. 2 – Design Strength • L is the length of the connection, which for this case will be equal to 2 x 75 = 150 mm. • • • Effective net area = Ae = 0. 809 x 1677. 1 in 2 = 1357 mm 2 • Net section fracture = t Ae Fu = 0. 75 x 1357 x 400/1000 = 407. 1 k. N • • Design strength = 407. 1 k. N Gross yielding design strength = t Ag Fy = 0. 9 x 1850 x 248/1000 = 412. 9 k. N (net section fracture governs) (Lower of the two values) 68402 37

Ex. 2. 3 – Design Strength l Determine the design strength of an ASTM A 992 W 8 x 24 with four lines if 20 mm diameter bolts in standard holes, two per flange, as shown in the Figure below. Assume the holes are located at the member end & the connection length is 225 mm. Also calculate at what length this tension member would cease to satisfy the slenderness limitation in LRFD specification. db = 20 mm 75 mm 68402 38

Ex. 2. 3 – Design Strength • • For ASTM A 992 material: Fy = 344 MPa; & Fu = 448 MPa • Gross yielding design strength = t Pn = t Ag Fy = 0. 90 x 4570 x 344/1000 = 1414. 9 k. N • Net section fracture strength = t Pn = t Ae Fu = 0. 75 x Ae x 448 For the W 8 x 24 section: • Ag = 4570 mm 2 d = 201 mm. • tw = 6. 2 mm. bf = 165 mm. • tf = 10. 2 mm. ry = 40. 9 mm. • • Ae = U A n for bolted connection An = Ag – (no. of holes) x (diameter of hole) x (thickness of flange) An = 4570 – 4 x (20+3. 2) x 10. 2. An = 3623 mm 2 68402 39

Ex. 2. 3 – Design Strength • • • What is for this situation? is the distance from the edge of the flange to the centroid of the half (T) section • • 68402 40

Special Cases for Welded Connections l If some elements of the cross section are not connected, then Ae will be less than An l For a rectangular bar or plate Ae will be equal to An l However, if the connection is by longitudinal welds at the ends as shown in the figure below, then Ae = UAg l Where, U = 1. 0 for L ≥ 2 w U = 0. 87 for 1. 5 w ≤ L < 2 w U = 0. 75 for w ≤ L < 1. 5 w l L = length of the pair of welds ≥ w l w = distance between the welds or width of plate/bar 68402 41

Ex. 2. 3 – Design Strength • The calculated value is not accurate due to the deviations in the geometry • • But, U ≤ 0. 90. Therefore, assume U = 0. 90 68402 42

Ex. 2. 3 – Design Strength • Net section fracture strength = t Ae Fu = 0. 75 x 0. 9 x 3623 x 448/1000 = 1095. 6 k. N • The design strength of the member is controlled by net section fracture = 1095. 6 k. N • According to LRFD specification, the maximum unsupported length of the member is limited to 300 ry = 300 x 40. 9 = 12270 mm = 12. 27 m. 68402 43

Special Cases for Welded Connections 68402 44

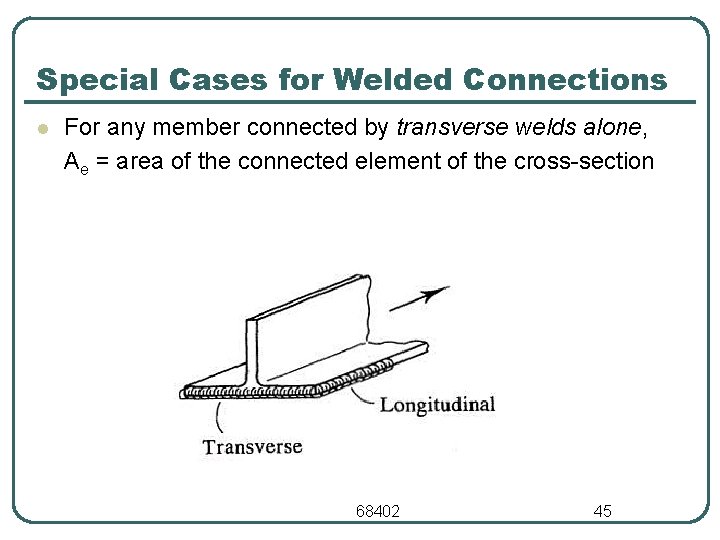
Special Cases for Welded Connections l For any member connected by transverse welds alone, Ae = area of the connected element of the cross section 68402 45

U for Welded Connections OR l Two major groups of welded connections • • General case • W, M and S shapes and T cut from them connected in flange with • All other shapes Special case for plates welded at their ends W L • Any member with transverse welds all around ONLY 68402 46

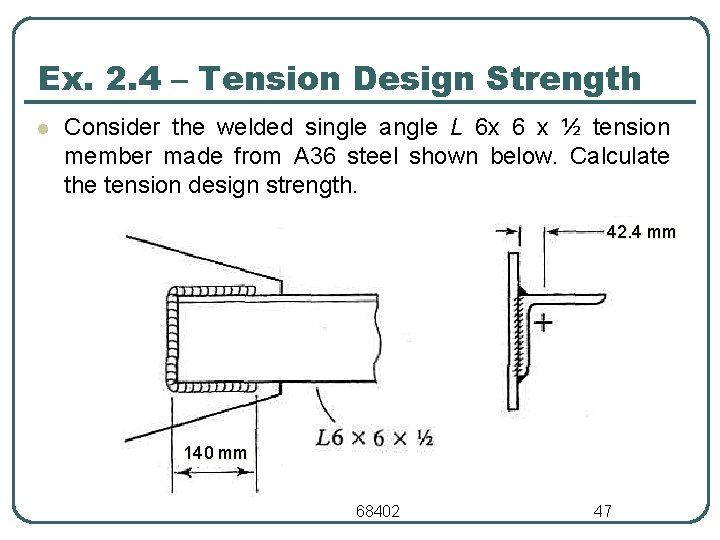
Ex. 2. 4 – Tension Design Strength l Consider the welded single angle L 6 x 6 x ½ tension member made from A 36 steel shown below. Calculate the tension design strength. 42. 4 mm 140 mm 68402 47

Ex. 2. 4 – Tension Design Strength • • • Ag = 3720 mm 2 An = 3720 mm 2 - because it is a welded connection Ae = U A n • • • = 42. 4 mm for this welded connection L = 152 mm for this welded connection • Gross yielding design strength = t Fy Ag = 0. 9 x 248 x 3720/1000 = 830 k. N • Net section fracture strength = t Fu Ae = 0. 75 x 400 x 0. 72 x 3720/1000 = 803 k. N • Design strength = 803 k. N (net section fracture governs) 68402 48

Design of Tension Members l The design of a tension member involves finding the lightest steel section (angle, wide flange, or channel section) with design strength ( Pn) greater than or equal to the maximum factored design tension load (Pu) acting on it. • • Pn ≥ Pu • Pn is the design strength based on the gross section yielding, net section fracture & block shear rupture limit states. Pu is determined by structural analysis for factored load combinations 68402 49

Design of Tension Members l l For net section fracture limit state, Pn = 0. 75 x Ae x Fu • • Therefore, 0. 75 x Ae x Fu ≥ Pu • • But, Ae = U An U & An depend on the end connection. Therefore, Ae ≥ Thus, designing the tension member goes hand in hand with designing the end connection, which we have not covered so far. 68402 50

Design of Tension Members l Therefore, for this chapter of the course, the end connection details will be given in the examples & problems. l The AISC manual tabulates the tension design strength of standard steel sections • Include: wide flange shapes, angles, tee sections, & double angle sections. • The gross yielding design strength & the net section fracture strength of each section is tabulated. • This provides a great starting point for selecting a section. 68402 51

Design of Tension Members l There is one serious limitation • The net section fracture strength is tabulated for an assumed value of U = 0. 75, obviously because the precise connection details are not known • For all W, Tee, angle & double angle sections, Ae is assumed to be = 0. 75 Ag • The engineer can first select the tension member based on the tabulated gross yielding & net section fracture strengths, & then check the net section fracture strength & the block shear strength using the actual connection details. 68402 52

Design of Tension Members l Additionally for each shape, the code tells the value of Ae below which net section fracture will control: • Thus, for Grade 50 steel sections, net section fracture will control if Ae < 0. 923 Ag • For Grade 36 steel sections, net section fracture will control if Ae < 0. 745 Ag l Slenderness limits • Tension member slenderness l/r must preferably be limited to 300 as per LRFD specifications. 68402 53

Slenderness Requirements l Although tension elements are not likely to buckle, it is recommended to limit their slenderness ratio to 300 l The slenderness limitation of tension members is not for structural integrity as for compression members. l The reason for the code limitation is to assure that the member has enough stiffness to prevent lateral movement or vibration. l This limitation does not apply to tension rods and cables. 68402 54

Steps for Design of Tension Members l Steps for design • • • Calculate the load Decide whether your connection will be welded or bolted Assume U factor of 0. 75 Determine the gross area of the element Assume An = 0. 75 Ag 68402 55

Steps for Design of Tension Members l Steps for design • • Choose the lightest section with area little larger than Ag • Check slenderness ratio Calculate, Ag, An, U and Ae for the chosen section 68402 56

Ex. 2. 7 – Design of Tension Members l l Design a member to carry a factored maximum tension load of 350 k. N. Assume that the member is a wide flange connected through the flanges using eight 20 mm diameter bolts in two rows of four each as shown in the figure below. The center to center distance of the bolts in the direction of loading is 100 mm. The edge distances are 40 & 50 mm as shown in the figure below. Steel material is A 992 20 mm 50 mm 100 mm 40 mm Fy = 344 MPa Fu = 448 MPa 68402 57

Ex. 2. 7 – Design of Tension Members • Select a section from the Tables • Ag ≥ 350*1000/(0. 9*344) = 1130 mm 2. • Assume U=0. 75 • Ag 350*1000/(0. 45*448)=1736 mm 2 • Try W 8 x 10 with Ag = 1910 mm 2. • An = 1910 – 4*(23. 2*5. 2) = 1427 mm 2. • x = 24. 6 mm (students have to compute it) • U = 1 – 24. 6/100 = 0. 754 • Gross yielding strength = 591 k. N, & net section fracture strength = 362 k. N 68402 58

Extra Slides 68402 59

Block Shear l For some connection configurations, the tension member can fail due to ‘tear out’ of material at the connected end. This is called block shear. l For example, the single angle tension member connected as shown in the Fig. 2. 3 below is susceptible to the phenomenon of block shear. l For the case shown above, shear failure will occur along the longitudinal section a b & tension failure will occur along the transverse section b c. l AISC Specification on tension members does not cover block shear failure explicitly. But, it directs the engineer to the Specification on connections 68402 60

Block Shear Fig. 2. 3 Block shear failure of single angle tension member 68402 61

Block Shear l Block shear strength is determined as the sum of the shear strength on a failure path & the tensile strength on a perpendicular segment. • • • l Block shear strength = net section fracture strength on shear path + net section fracture strength of the tension path OR Block shear strength = gross yielding strength of the shear path + net section fracture strength of the tension path Which of the two calculations above governs? 68402 62

Block Shear Rn = (0. 6 Fu Anv + Ubs. Fu Ant) ≤ (0. 6 Fy. Agv + Ubs. Fu Ant) = 0. 75 Ubs = 1. 0 for uniform tensile stress; = 0. 5 for nonuniform tensile stress Agv - gross area subject to shear Agt - gross area subject to tension Anv - net area subject to shear Ant - net area subject to tension Fu - ultiamte strength of steel Fy - yield strength of steel 68402 63

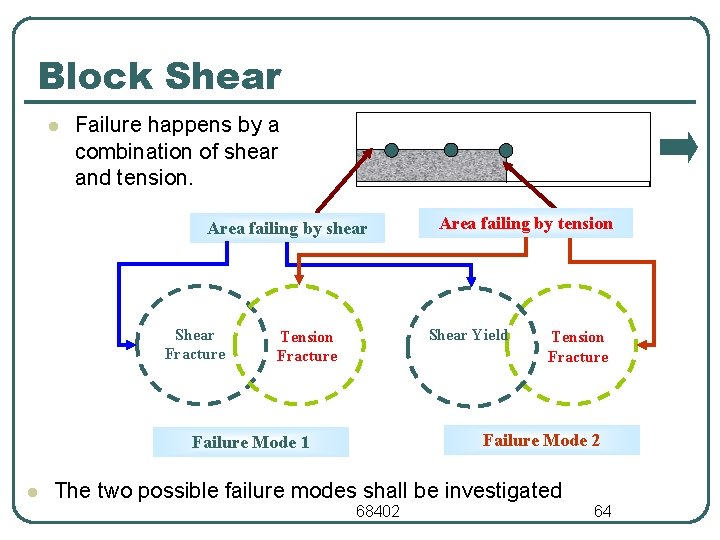
Block Shear l Failure happens by a combination of shear and tension. Area failing by shear Shear Fracture Shear Yield Tension Fracture Failure Mode 2 Failure Mode 1 l Area failing by tension The two possible failure modes shall be investigated 68402 64

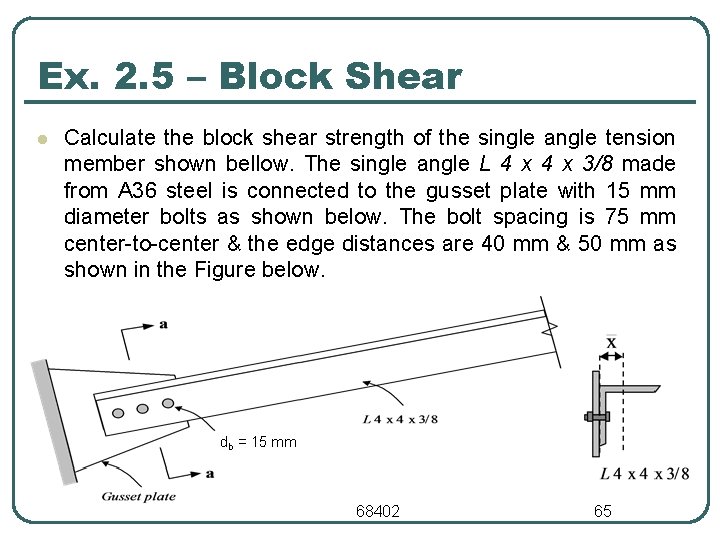
Ex. 2. 5 – Block Shear l Calculate the block shear strength of the single angle tension member shown bellow. The single angle L 4 x 3/8 made from A 36 steel is connected to the gusset plate with 15 mm diameter bolts as shown below. The bolt spacing is 75 mm center to center & the edge distances are 40 mm & 50 mm as shown in the Figure below. db = 15 mm 68402 65

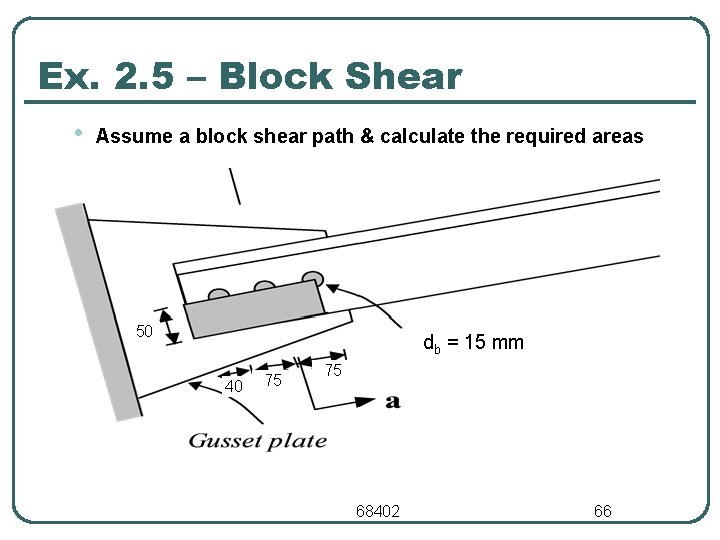
Ex. 2. 5 – Block Shear • Assume a block shear path & calculate the required areas 50 db = 15 mm 40 75 75 68402 66

Ex. 2. 5 – Block Shear • • • Agt = gross tension area = 50 x 9. 5 = 475 mm 2 Ant = net tension area = 475 0. 5 x (15 + 3. 2) x 9. 5 = 388. 5 mm 2 Agv = gross shear area = (75 +40) x 9. 5 = 1805 mm 2 Anv = net shear area = 1805 2. 5 x (15 + 3. 2) x 9. 5 = 1372. 8 mm 2 Ubs = 1. 0 Calculate block shear strength • t Rn = 0. 75 (0. 6 Fu Anv + Ubs. Fu Ant) • t Rn = 0. 75 (0. 6 x 400 x 1372. 8 + 1. 0 x 400 x 388. 5)/1000 = 363. 7 k. N 68402 67

Ex. 2. 5 – Block Shear • Check upper limit • t Rn ≤ (0. 6 Fy. Agv + Ubs. Fu Ant) • t Rn ≤ 0. 75 (0. 6 x 248 x 1805 + 1. 0 x 400 x 388. 5)/1000 • t Rn ≤ 318 k. N • Block shear strength = 318 k. N 68402 68

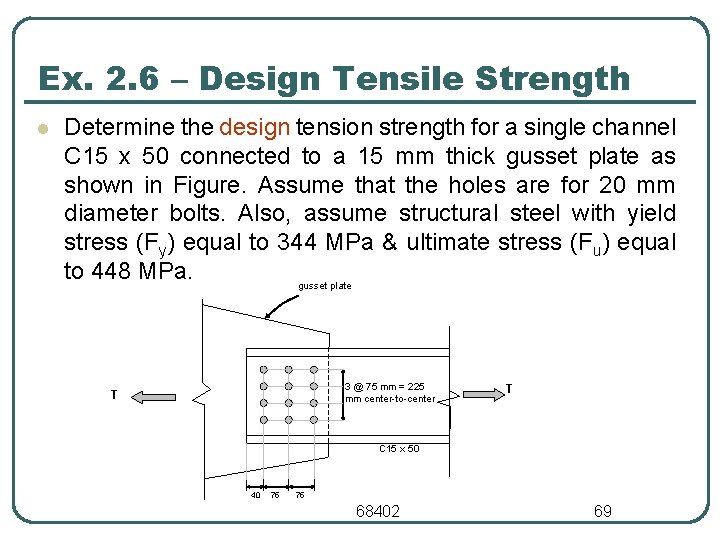
Ex. 2. 6 – Design Tensile Strength l Determine the design tension strength for a single channel C 15 x 50 connected to a 15 mm thick gusset plate as shown in Figure. Assume that the holes are for 20 mm diameter bolts. Also, assume structural steel with yield stress (Fy) equal to 344 MPa & ultimate stress (Fu) equal to 448 MPa. gusset plate 3 @ 75 mm = 225 mm center to center T T C 15 x 50 40 75 75 68402 69

Ex. 2. 6 – Design Tensile Strength • Limit state of yielding due to tension: • Limit state of fracture due to tension: • Check: • Note: The connection eccentricity, x, for a C 15 X 50 can be found in section property tables. OK. 68402 70

Ex. 2. 6 – Design Tensile Strength • Limit state of block shear rupture: • Agt = gross tension area = 225 x 18. 2 = 4095 mm 2 • Ant = net tension area = (225 3*(23. 2))*18. 2 = 2828 mm 2 • Agv = gross shear area = 2*(190*18. 2) = 6916 mm 2 • Anv = net shear area = 2*((190 2. 5*23. 2) *18. 2) = 4805 mm 2 • Ubs = 1. 0 • Calculate block shear strength • • t Rn = 0. 75 (0. 6 Fu Anv + Ubs. Fu Ant) t Rn = 0. 75 (0. 6 x 448 x 4805 + 1. 0 x 448 x 2828)/1000 = 1919 k. N 68402 71

Ex. 2. 6 – Design Tensile Strength • Check upper limit • • • t Rn ≤ (0. 6 Fy. Agv + Ubs. Fu Ant) t Rn ≤ 0. 75 (0. 6 x 344 x 6916 + 1. 0 x 448 x 2828) t Rn ≤ 2021 k. N Block shear strength = 1919 k. N Block shear rupture is the critical limit state & the design tension strength is 1919 k. N. 68402 72

Staggered Bolts 68402 73

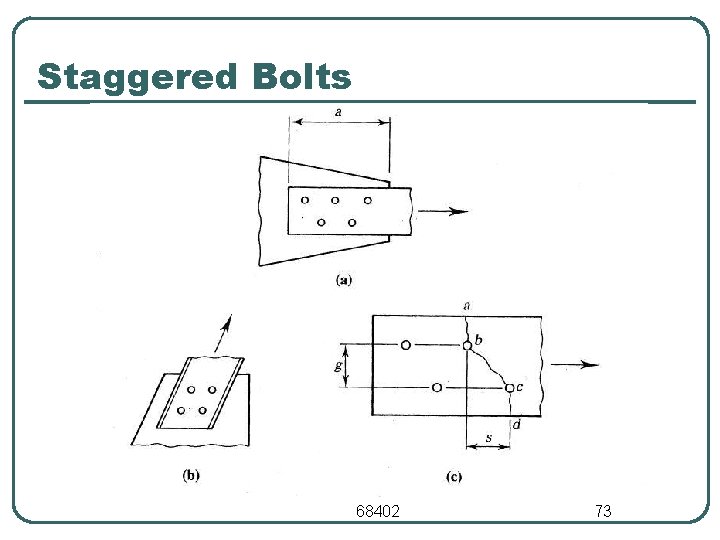
Staggered Bolts l For a bolted tension member, the connecting bolts can be staggered for several reasons: • • • To get more capacity by increasing the effective net area To achieve a smaller connection length To fit the geometry of the tension connection itself. l For a tension member with staggered bolt holes (see example figure above), the relationship f = P/A does not apply & the stresses are a combination of tensile & shearing stresses on the inclined portion b-c. l Net section fracture can occur along any zig zag or straight line. For ex. , fracture can occur along the inclined path a-b-c-d in the figure above. However, all possibilities must be examined. 68402 74

Staggered Bolts l Empirical methods have been developed to calculate the net section fracture strength. • net width = gross width d - the diameter of hole to be deducted (db + 3. 2 mm) s 2/4 g - added for each gage space in the chain being considered s - the longitudinal spacing (pitch) of the bolt holes in the direction of loading g - the transverse spacing (gage) of the bolt holes perpendicular to loading direction. net area (An) = net width x plate thickness effective net area (Ae) = U An where net fracture design strength = t Ae Fu ( t = 0. 75) 68402 75

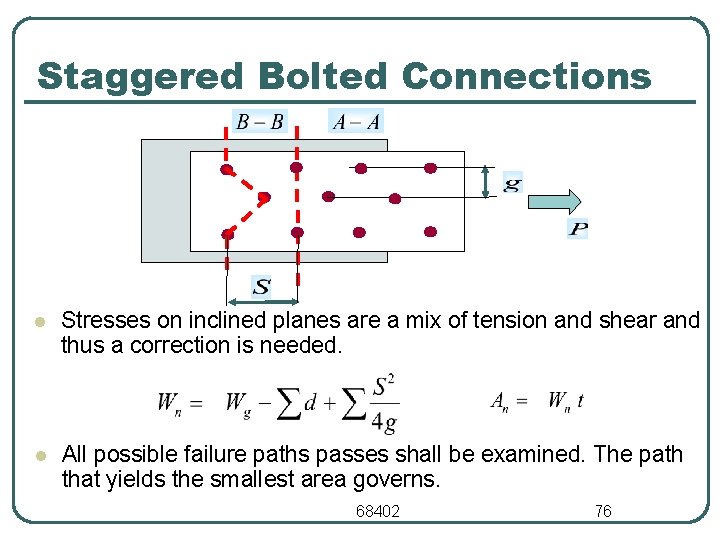
Staggered Bolted Connections l Stresses on inclined planes are a mix of tension and shear and thus a correction is needed. l All possible failure paths passes shall be examined. The path that yields the smallest area governs. 68402 76