4 600 04 Modles daide la dcision Sance

4 -600 -04 Modèles d’aide à la décision Séance 12 Optimisation non linéaire 1

Gestion de projet (2ème partie) Plan 12. 1 Introduction 12. 2 Problème du lot économique 12. 3 Problème de localisation 12. 4 Problème de sélection d’un portefeuille 2

12. 1 Introduction • Dans les problèmes de gestion, il arrive parfois que les relations entre les variables soient non-linéaires. • Dans un modèle mathématique, la fonction-objectif et/ou les contraintes pourront être non-linéaires. • Dans Excel, les programmes non-linéaires (PNL) se formulent et s’implantent de façon très similaire aux programmes linéaires (PL). • Mais les méthodes mathématiques utilisées pour résoudre les PNL sont passablement différentes des méthodes utilisées pour résoudre les PL. (C’est plus long!) • Le Solveur essaie de cacher ces différences mais il existe des difficultés importantes dans la résolution de PNL. 3

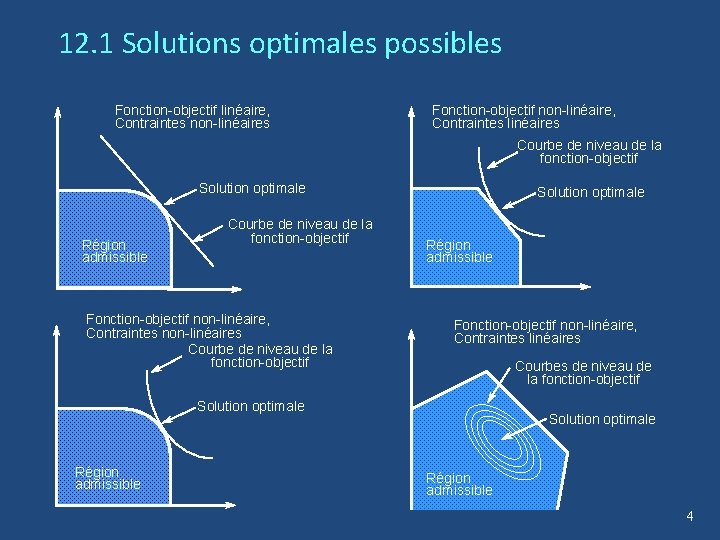
12. 1 Solutions optimales possibles Fonction-objectif linéaire, Contraintes non-linéaires Fonction-objectif non-linéaire, Contraintes linéaires Courbe de niveau de la fonction-objectif Solution optimale Région admissible Courbe de niveau de la fonction-objectif Fonction-objectif non-linéaire, Contraintes non-linéaires Courbe de niveau de la fonction-objectif Solution optimale Région admissible Fonction-objectif non-linéaire, Contraintes linéaires Courbes de niveau de la fonction-objectif Solution optimale Région admissible 4

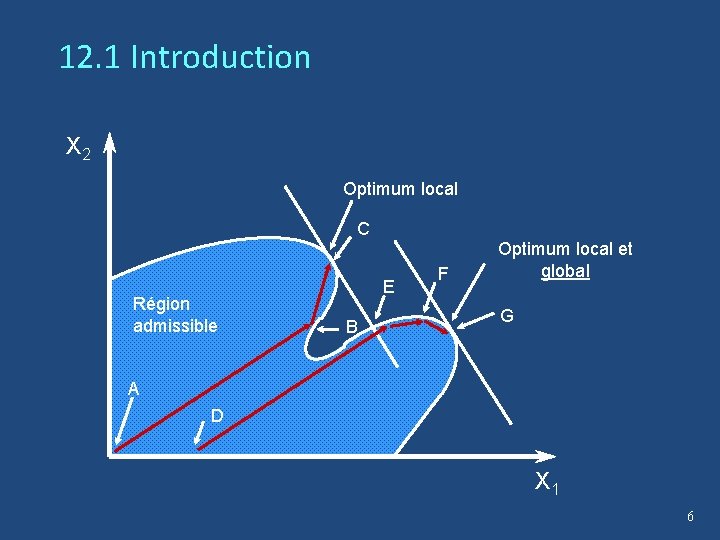
12. 1 Introduction • La méthode utilisée par le Solveur d’Excel peut se terminer en une solution optimale locale. Ainsi, elle ne garantit pas de trouver la solution optimale globale du problème. • Le point de départ influence la solution optimale locale obtenue (lorsqu’il y a plusieurs optima locaux). 5

12. 1 Introduction X 2 Optimum local C Région admissible E B F Optimum local et global G A D X 1 6

12. 1 Introduction 7

12. 2 Problème du lot économique • On utilise un certain produit. • L’approvisionnement : Commandes régulièrement à un fournisseur. (Coût d’approvisionnement) • Le fournisseur nous facture des frais de livraison chaque fois qu’on utilise ses services. (Coût de livraison) • La commande est stockée en entrepôt en attendant son utilisation. (Coûts de stockage qui dépendent de la quantité stockée et durée de stockage) 8

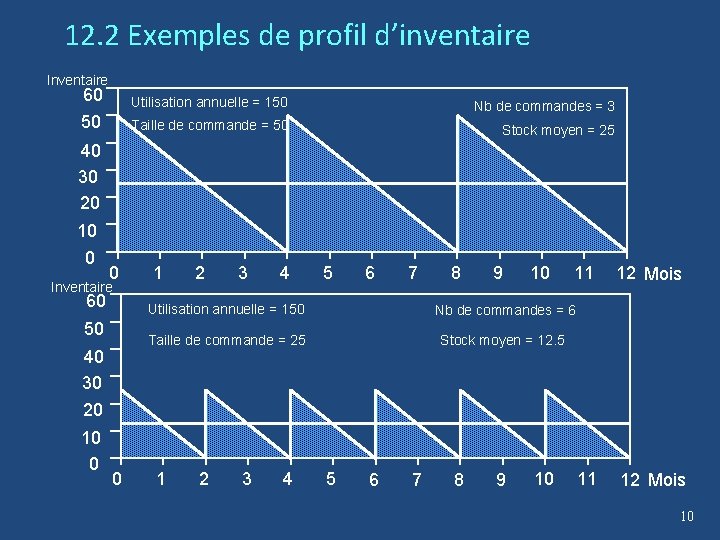
12. 2 Problème du lot économique • Le niveau de stock dans un entrepôt peut être représenté par un graphique en dents de scie (voir p. suivante) • La structure de coûts dans un tel système comprend des coûts de livraison, d’acquisition et de stockage. – Les coûts annuels de livraison sont 2 fois plus petits dans le 1 er graphique. – Les coûts annuels d’acquisition sont identiques. – Les coûts annuels de stockages sont plus gros dans le 1 er graphique. 9

12. 2 Exemples de profil d’inventaire Inventaire 60 Utilisation annuelle = 150 50 Nb de commandes = 3 Taille de commande = 50 Stock moyen = 25 40 30 20 10 0 0 Inventaire 60 50 40 30 20 10 0 0 1 2 3 4 5 6 7 8 9 10 11 Utilisation annuelle = 150 Nb de commandes = 6 Taille de commande = 25 Stock moyen = 12. 5 1 2 3 4 5 6 7 8 9 10 11 12 Mois 10

12. 2 Problème du lot économique Hypothèses : – La demande est répartie uniformément durant l’année. – Chaque commande est reçue exactement au moment où le niveau d’inventaire tombe à 0. D = demande annuelle (donnée). C = coût unitaire d’achat (donnée). F = coût fixe pour passer une commande (donnée). S = coût de stockage (exprimé en % de C) (donnée). q = taille d’une commande (Variable de décision). 11

12. 2 Problème du lot économique • Exemple Ragsdale p. 346 – Alan Wang achète du papier pour alimenter les photocopieurs et les imprimantes laser de Metro. Bank. • Demande annuelle est de 24 000 boîtes • Coût unitaire d’achat est de 35$ • Coût fixe de commande est de 50$ • Coût d’inventaire correspond à 18% du coût d’achat – Quel est le lot économique? 12

12. 2 Problème du lot économique Définition de la variable de décision: q = taille d’une commande Fonction-Objectif: Minimiser le coût total MIN [ 24000(35) + 24000(50)/q + 18% * (35)*q/2 ] MIN 840000 + 1200000/q + 3, 15 q Contraintes: q ≥ 1 (au moins une boîte dans une commande ? ? ? ) 13

12. 2 Problème du lot économique • Par le calcul différentiel, on peut démontrer que la valeur optimale de q est : • Ou on peut utiliser le solveur d’Excel! (Voir fichier 4600 -12. 3 -Lot_Econ-Sol. xls) 14

12. 4 Problème de localisation • Plusieurs problèmes de décision consistent à déterminer la localisation optimale d’une installation : – – – usine de production, entrepôt, centre de distribution, caserne de pompiers, Etc. • Ces problèmes nécessitent parfois l’utilisation d’une mesure de distance dans la fonction objectif et/ou les contraintes. • Rappelons que la distance à vol d’oiseau (dist. euclidienne) entre deux points (X 1, Y 1) et (X 2, Y 2) se calcule : 15

12. 4 Problème de localisation • Cas Rappaport Communications (inspiré de Ragsdale, p. 350) – Rappaport Communications fournit un service de téléphonie cellulaire dans différents états américains. – La compagnie veut étendre son service à quatre villes de l’Ohio. – Une nouvelle tour doit être construite pour prendre en charge les communications entre les tours déjà existantes situées dans les 4 villes. 16

12. 4 Problèmes de localisation Y 50 Cleveland x=5, y=45 40 30 Youngstown Akron x=12, y=21 20 x=52, y=21 10 Canton x=17, y=5 0 0 10 20 30 40 50 60 X 17

12. 4 Problèmes de localisation 1. Trouver l’emplacement de la nouvelle tour qui minimise la somme des distances entre cette tour et les 4 tours actuelles. 2. Comment modifier le modèle si on considère que la tour a un rayon de transmission de 30 miles? 18

12. 4 Problèmes de localisation Q 1: Définition des variables de décision : X : position de la nouvelle tour selon l’axe des X Y : position de la nouvelle tour selon l’axe des Y Fonction-Objectif: MIN Aucune contrainte 19

12. 4 Problèmes de localisation Q 2: Ajouter les contraintes non-linéaires suivantes au modèle de la question 1 Cleveland : … Youngstown: 20

12. 5 Sélection d’un portefeuille • Un investisseur, disposant d’un budget donné, souhaite se constituer un portefeuille. • Il peut choisir entre n titres différents. • Comment constituer son portefeuille de façon à minimiser son risque tout en se garantissant un certain rendement espéré minimal ? • Ceci peut se traduire sous forme d’un modèle non-linéaire (modèle de Markowitz). 21

12. 5 Sélection d’un portefeuille • Variables : pi : proportion du budget investi dans le titre i (i=1, …, n)Fonction-objectif : On cherche à minimiser le risque (variance du portefeuille) : Min où: σi 2 est la variance du titre i σij est la covariance entre les titres i et j. 22

12. 5 Sélection d’un portefeuille • Contraintes: – Rendement espéré minimum: r 1 p 1 + … + rnpn ≥ rmin (ri = rendement espéré du titre i) – Contrainte de budget: p 1 + … + p n = 1 – Diverses contraintes sur la constitution du portefeuille. Par exemple: 0 ≤ pi ≤ ui (ui = proportion maximale du titre i) 23

12. 5 Sélection d’un portefeuille • Un petit exemple à 2 titres: – – – – Rendement espéré du titre 1 : 6% Rendement espéré du titre 2 : 2% Rendement espéré minimum : 3% Investissement maximum du titre 1 : 75% du portefeuille Investissement maximum du titre 2 : 90% du portefeuille Variance du titre 1 : 0, 09 Variance du titre 2 : 0, 06 Covariance des titres 1 et 2 : 0, 02 24

12. 5 Sélection d’un portefeuille 25

12. 5 Sélection d’un portefeuille Avec Excel : En français SOMMEPROD(PRODUITMAT(p; Cov); p) En anglais SUMPRODUCT(MMULT(p; Cov); p) 26

12. 5. 2 Exemple avec trois titres et données antérieures (Ragsdale, p. 368) • Un planificateur financier désire constituer un portefeuille le moins risqué possible avec un rendement espéré minimum de 12% en utilisant les titres suivants : Rendement annuel Année IBC NMC NBS 1 11. 2% 8. 0% 10. 9% 2 10. 8% 9. 2% 22. 0% 3 11. 6% 6. 6% 37. 9% 4 -1. 6% 18. 5% -11. 8% 5 -4. 1% 7. 4% 12. 9% 6 8. 6% 13. 0% -7. 5% 7 6. 8% 22. 0% 9. 3% 8 11. 9% 14. 0% 48. 7% 9 12. 0% 20. 5% -1. 9% 10 8. 3% 14. 0% 19. 1% 11 6. 0% 19. 0% -3. 4% 12 10. 2% 9. 0% 43. 0% 27

12. 5. 2 Le modèle A À calculer : n Rendement moyen ri n Matrice Cov des variancescovariances 28

12. 5. 2 Le modèle B • Faisons comme si on avait mis une proportion pi du budget dans le titre i. • Le rendement à l’an j aurait été: • Il nous reste à minimiser la variance de ces rendements sous la contrainte que la moyenne doit être supérieure à 0, 12. 29

12. 5. 3 Modélisation des deux objectifs avec une fonction d’utilité • Au lieu d’imposer une contrainte sur un taux de rendement espéré minimum, on peut vouloir considérer les deux objectifs contradictoires (Max Rendement et Min Risque) simultanément en modifiant le modèle non-linéaire de la façon suivante : – Fonction-objectif devient : MAX (1 -k)(Rendement espéré) - k(Variance) Où 0 ≤ k ≤ 1 est la constante d’aversion au risque définie par l’investisseur. – Retrait de la contrainte de rendement moyen minimum. 30