16 CLASSICAL CONFIGURATIONS Fano plane 73 We can

16. CLASSICAL CONFIGURATIONS

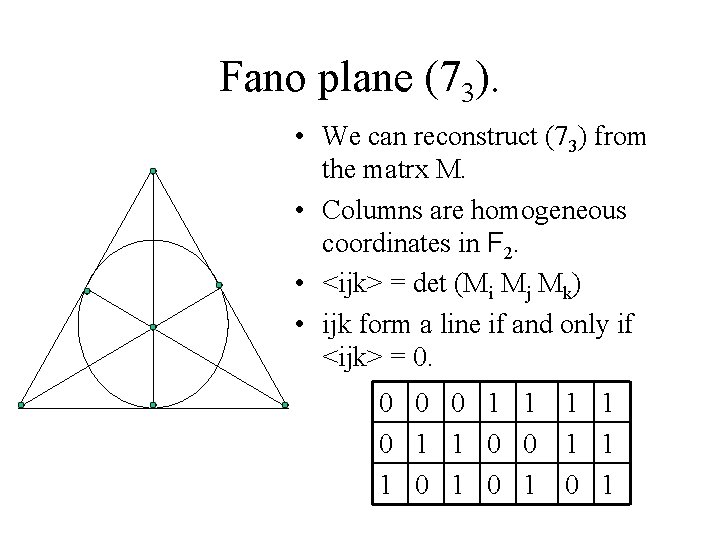
Fano plane (73). • We can reconstruct (73) from the matrx M. • Columns are homogeneous coordinates in F 2. • <ijk> = det (Mi Mj Mk) • ijk form a line if and only if <ijk> = 0. 0 0 0 1 1 0 0 1 0 1 1 1 0 1

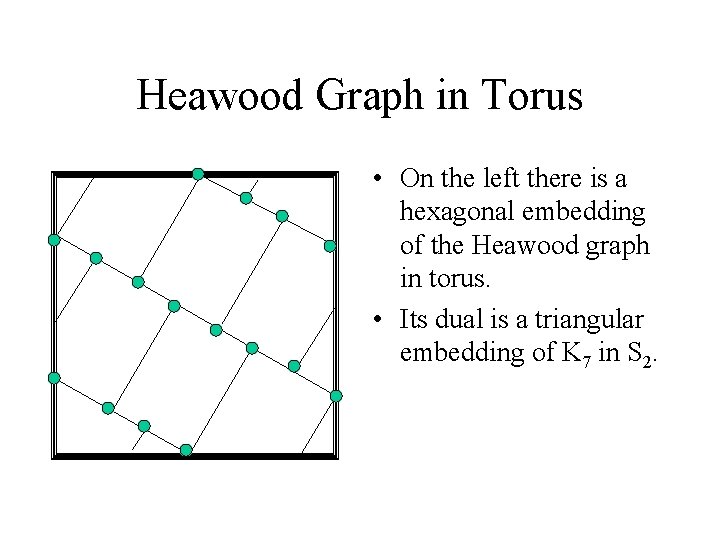
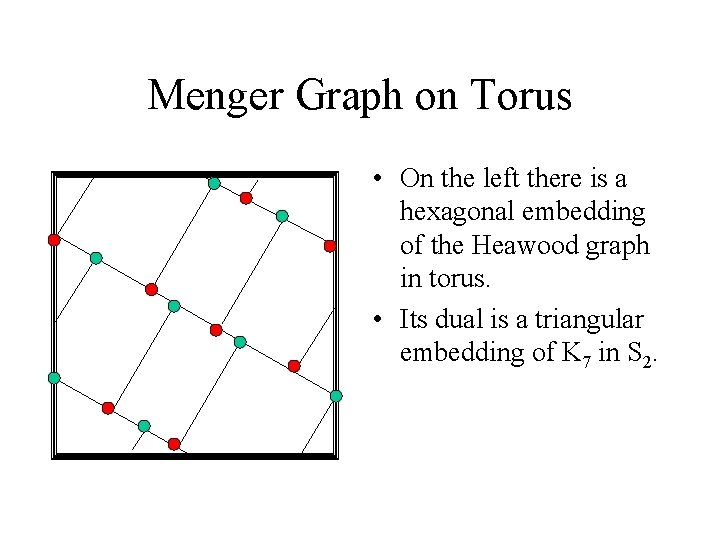
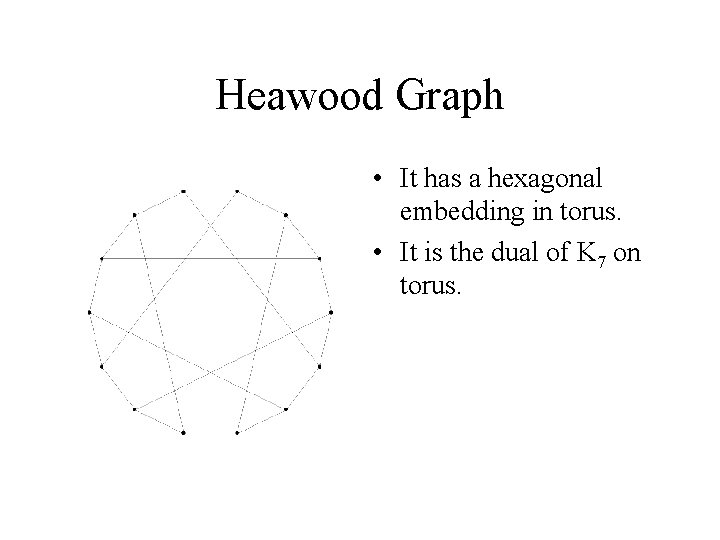
Heawood Graph in Torus • On the left there is a hexagonal embedding of the Heawood graph in torus. • Its dual is a triangular embedding of K 7 in S 2.

Torus Drawing Exercises • Given torusdraw. m we explore some of its feautres. • Tube[f, r] represents a tube along the curve f with radius r.

Torus Drawing Exercises • For example for trefoil[t] = {Sin[3 t], Sin[t] + 2 Sin[2 t], Cos[t] - 2 Cos[2 t]}. • Tube[trefoil, 0. 75] produces the bottom Figure.

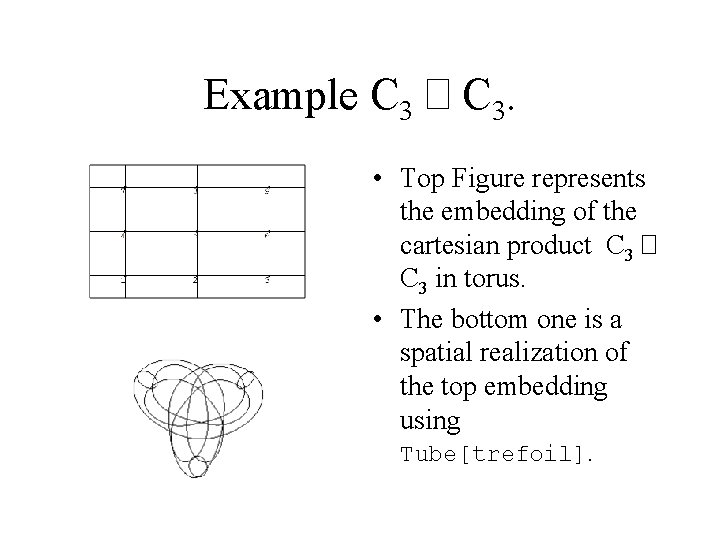
Example C 3 � C 3. • Top Figure represents the embedding of the cartesian product C 3 � C 3 in torus. • The bottom one is a spatial realization of the top embedding using Tube[trefoil].

Surface + Graph • By drawing the surface and the graph together we obtain the figure on the left.

Ordinary Torus

Menger Graph on Torus • On the left there is a hexagonal embedding of the Heawood graph in torus. • Its dual is a triangular embedding of K 7 in S 2.

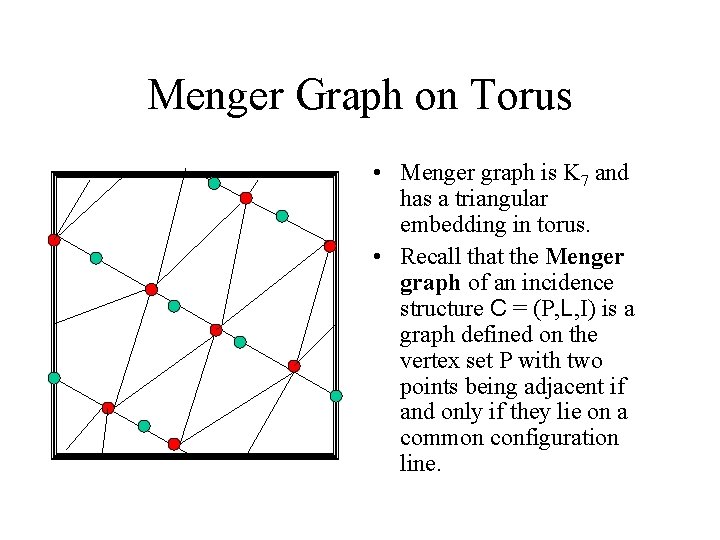
Menger Graph on Torus • Menger graph is K 7 and has a triangular embedding in torus. • Recall that the Menger graph of an incidence structure C = (P, L, I) is a graph defined on the vertex set P with two points being adjacent if and only if they lie on a common configuration line.

Genus of Menger Graph • Let L be the Levi graph and M be the Menger graph of a (vr, b 3) configuration. Then g(M) · g(L), where g(G) denotes the genus of G.

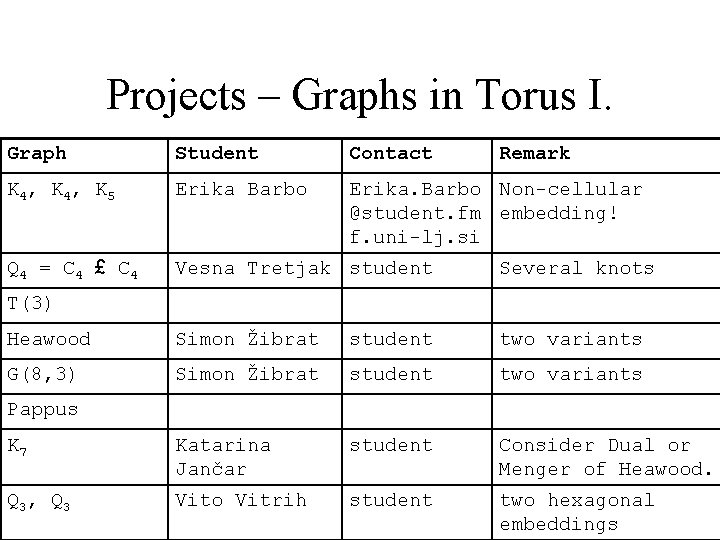
Projects – Graphs in Torus I. Graph Student Contact Remark K 4, K 5 Erika Barbo Erika. Barbo Non-cellular @student. fm embedding! f. uni-lj. si Q 4 = C 4 £ C 4 Vesna Tretjak student Several knots Heawood Simon Žibrat student two variants G(8, 3) Simon Žibrat student two variants K 7 Katarina Jančar student Consider Dual or Menger of Heawood. Q 3, Q 3 Vito Vitrih student two hexagonal embeddings T(3) Pappus

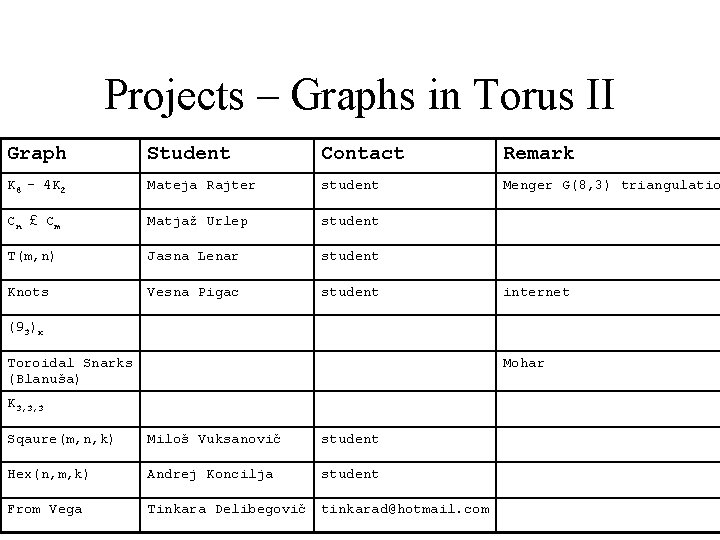
Projects – Graphs in Torus II Graph Student Contact Remark K 8 - 4 K 2 Mateja Rajter student Menger G(8, 3) triangulatio Cn £ C m Matjaž Urlep student T(m, n) Jasna Lenar student Knots Vesna Pigac student internet (93)x Toroidal Snarks (Blanuša) Mohar K 3, 3, 3 Sqaure(m, n, k) Miloš Vuksanovič student Hex(n, m, k) Andrej Koncilja student From Vega Tinkara Delibegovič tinkarad@hotmail. com

Projects – Graphs in Torus III. Graph Student Contact Remark Knight Graph Janez Groznik student Toroidal!! Double Torus Boštjan Ramšak student Combine two S 1. Experiment with knots. Double Torus G(8, 3) Cylinder Andrej Lindič student Ring Sabina Omahen student Several graphs

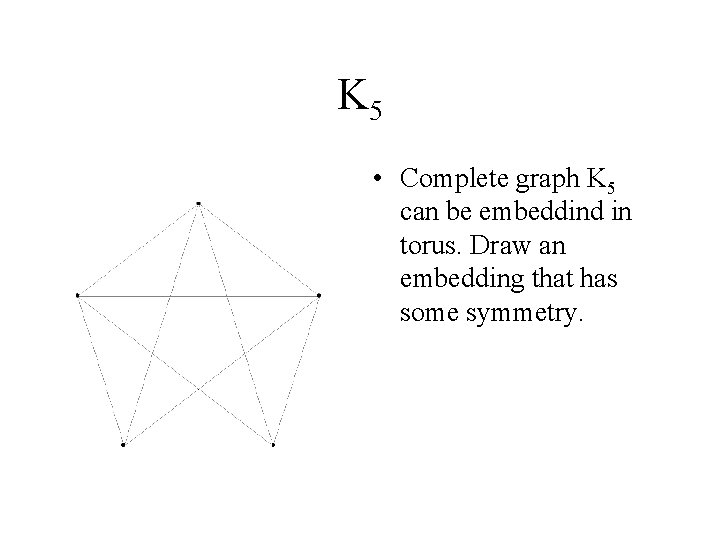
K 5 • Complete graph K 5 can be embeddind in torus. Draw an embedding that has some symmetry.

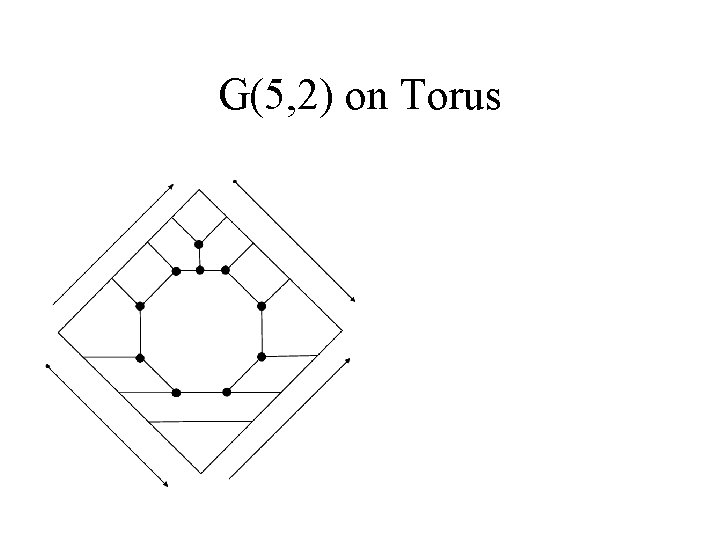
G(5, 2) on Torus

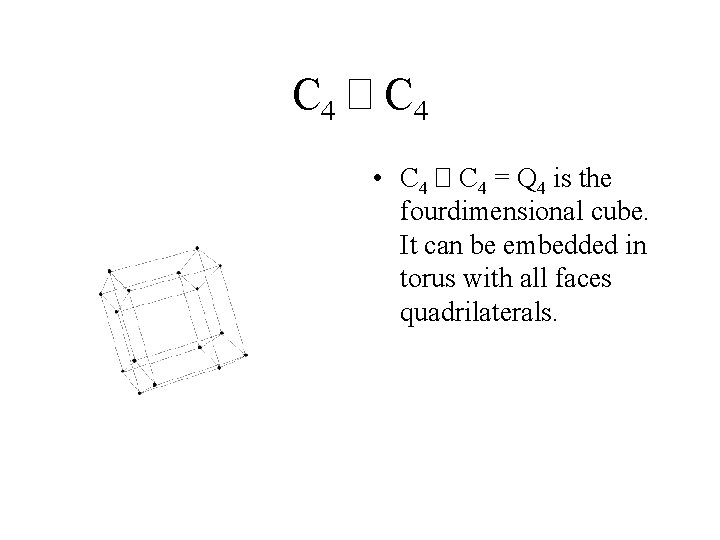
C 4 � C 4 • C 4 � C 4 = Q 4 is the fourdimensional cube. It can be embedded in torus with all faces quadrilaterals.

Heawood Graph • It has a hexagonal embedding in torus. • It is the dual of K 7 on torus.

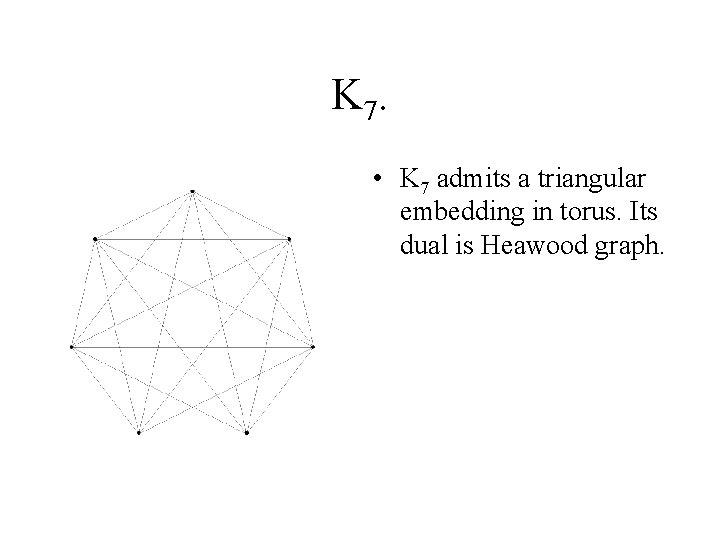
K 7. • K 7 admits a triangular embedding in torus. Its dual is Heawood graph.

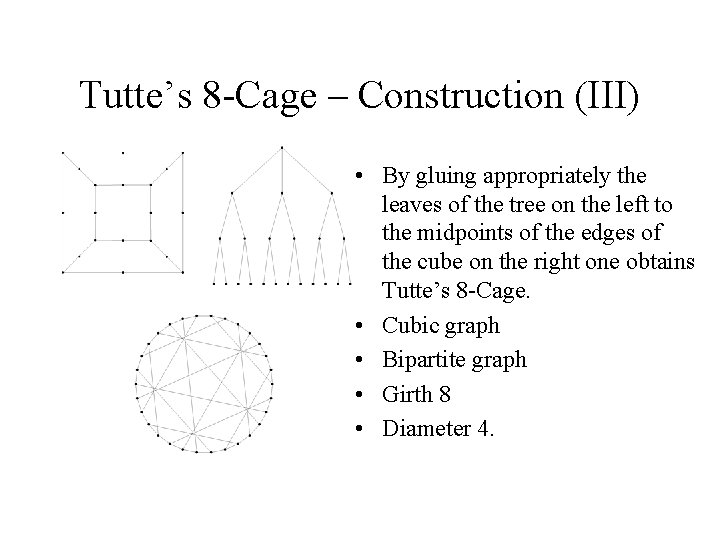
Tutte’s 8 -Cage – Construction (III) • By gluing appropriately the leaves of the tree on the left to the midpoints of the edges of the cube on the right one obtains Tutte’s 8 -Cage. • Cubic graph • Bipartite graph • Girth 8 • Diameter 4.

Question • Q. If we subdivide the edges of K 4 we may attach the tree on the left to it in such a way that we avoid quadrangles. What graph is produced in this way?

Möbius-Kantor Configuration – Revisited • Möbius-Kantor configuration is the only (83) configuration. Its Levi graph is the generalized Petersen graph G(8, 3). • The configuration has no geometric realization.

Complex Coordinatization of (94, 123)

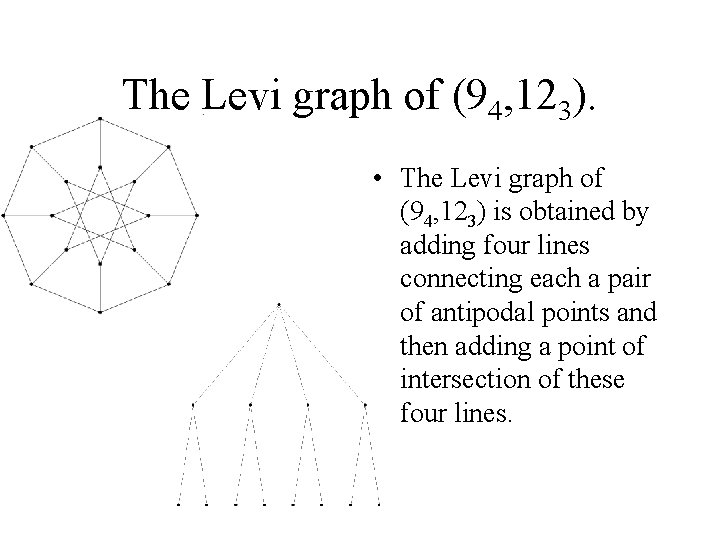
The Levi graph of (94, 123). • The Levi graph of (94, 123) is obtained by adding four lines connecting each a pair of antipodal points and then adding a point of intersection of these four lines.

A Z 3 coordinatization of (134) = PG(2, 3)

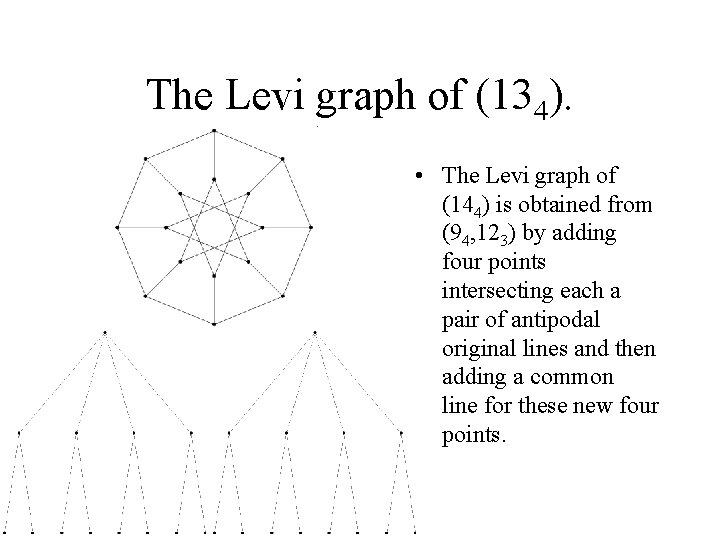
The Levi graph of (134). • The Levi graph of (144) is obtained from (94, 123) by adding four points intersecting each a pair of antipodal original lines and then adding a common line for these new four points.

Exercises • N 1. Show that by deleting any column of the matrix from the previous slide a coordinatization of (123, 94) is obtained. • N 2. Determine the homogeneous coordinates of the 9 lines from the previous problem. • N 3. Show that by deleting any column of the matrix for (94, 123) a coordinatization of (83) is obtained. • N 4. Given the Levi graph G(8, 3) of (83), determine the Levi graph of (94, 123).

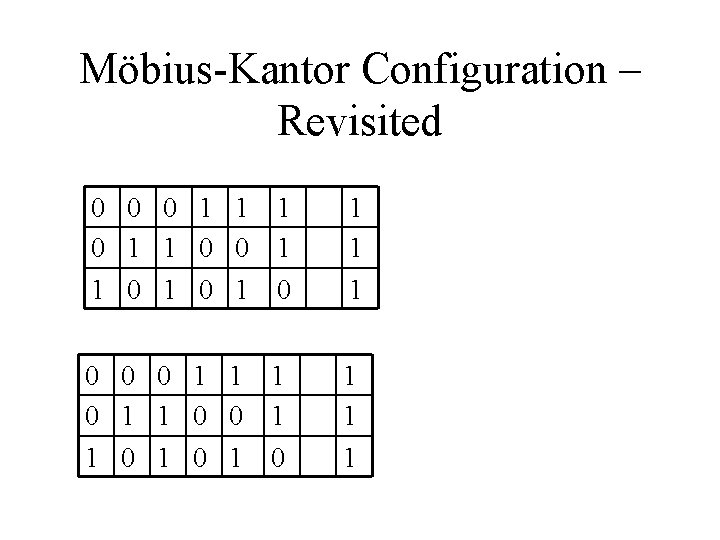
Möbius-Kantor Configuration – Revisited 0 0 0 1 1 1 0 0 1 1 0 1 0 1 0 1 1 1

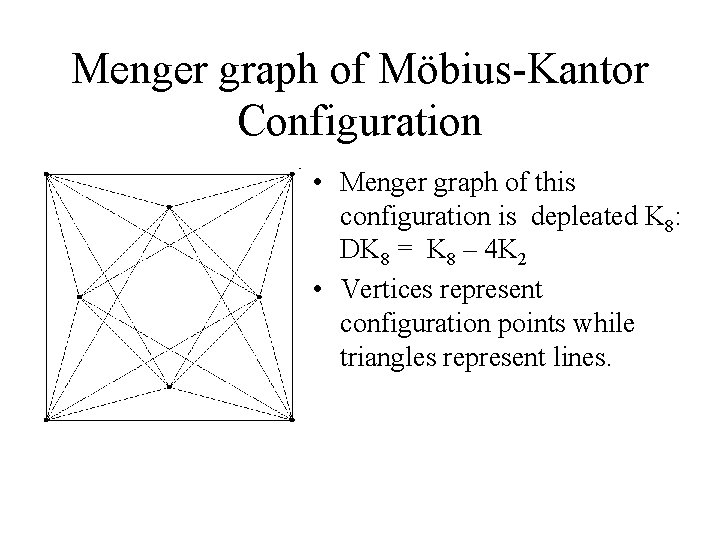
Menger graph of Möbius-Kantor Configuration • Menger graph of this configuration is depleated K 8: DK 8 = K 8 – 4 K 2 • Vertices represent configuration points while triangles represent lines.

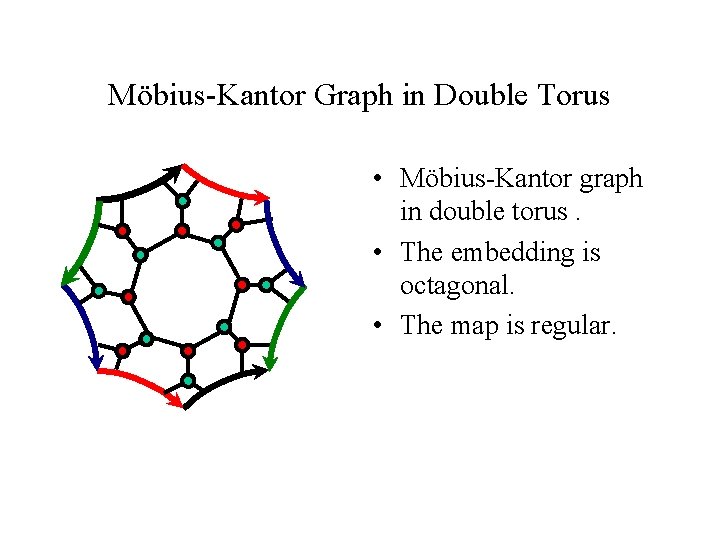
Möbius-Kantor Graph in Double Torus • Möbius-Kantor graph in double torus. • The embedding is octagonal. • The map is regular.

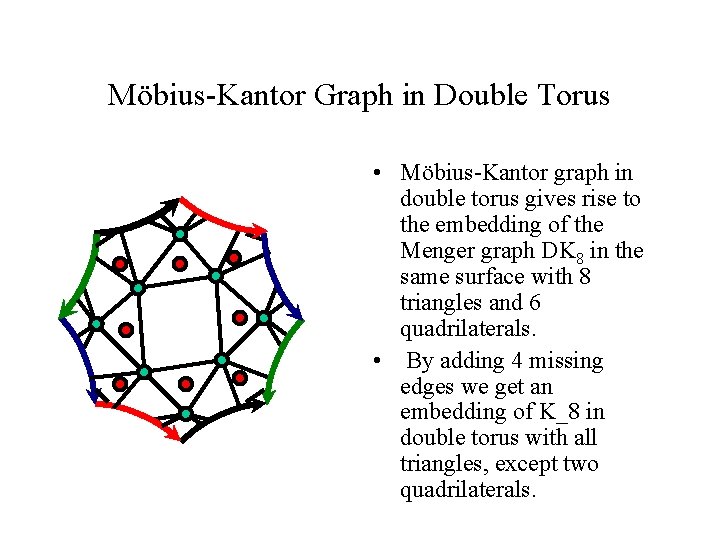
Möbius-Kantor Graph in Double Torus • Möbius-Kantor graph in double torus gives rise to the embedding of the Menger graph DK 8 in the same surface with 8 triangles and 6 quadrilaterals. • By adding 4 missing edges we get an embedding of K_8 in double torus with all triangles, except two quadrilaterals.

The Dual • The dual graph is S[2](K 4). • Let G be any graph. Recall that S(G) is the subdivision graph. • S[k](G) is obtained from S(G) by multiplying the original vertices of G k times.

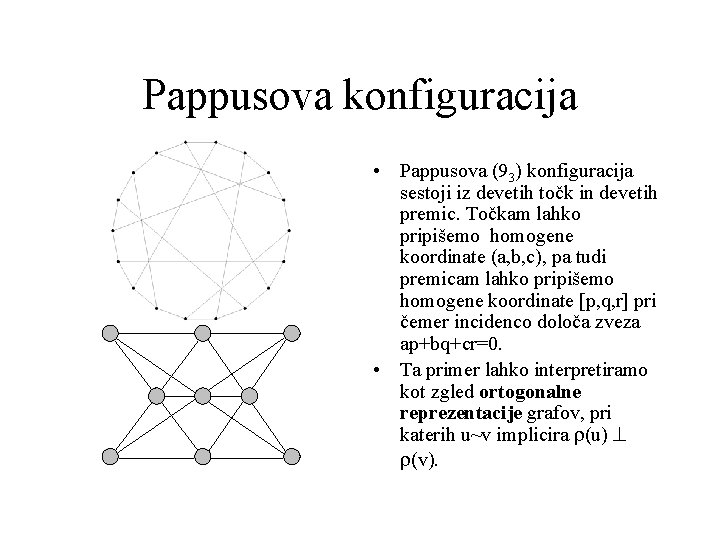
Pappusova konfiguracija • Pappusova (93) konfiguracija sestoji iz devetih točk in devetih premic. Točkam lahko pripišemo homogene koordinate (a, b, c), pa tudi premicam lahko pripišemo homogene koordinate [p, q, r] pri čemer incidenco določa zveza ap+bq+cr=0. • Ta primer lahko interpretiramo kot zgled ortogonalne reprezentacije grafov, pri katerih u~v implicira r(u) ^ r(v).

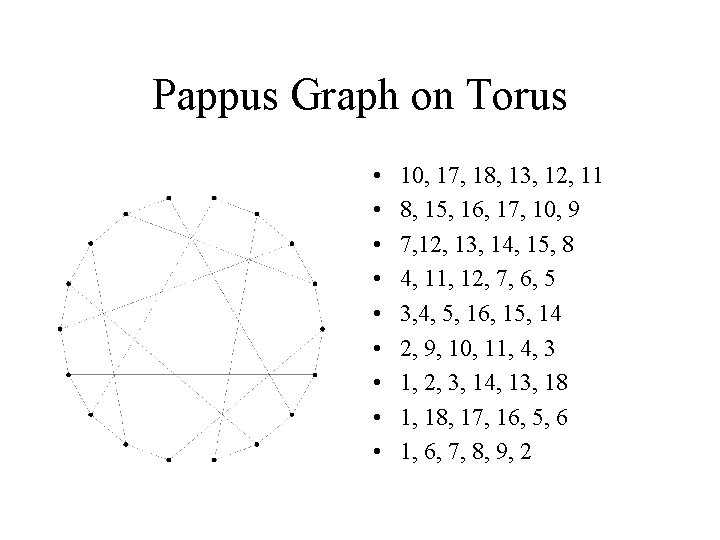
Pappus Graph on Torus • • • 10, 17, 18, 13, 12, 11 8, 15, 16, 17, 10, 9 7, 12, 13, 14, 15, 8 4, 11, 12, 7, 6, 5 3, 4, 5, 16, 15, 14 2, 9, 10, 11, 4, 3 1, 2, 3, 14, 13, 18 1, 18, 17, 16, 5, 6 1, 6, 7, 8, 9, 2

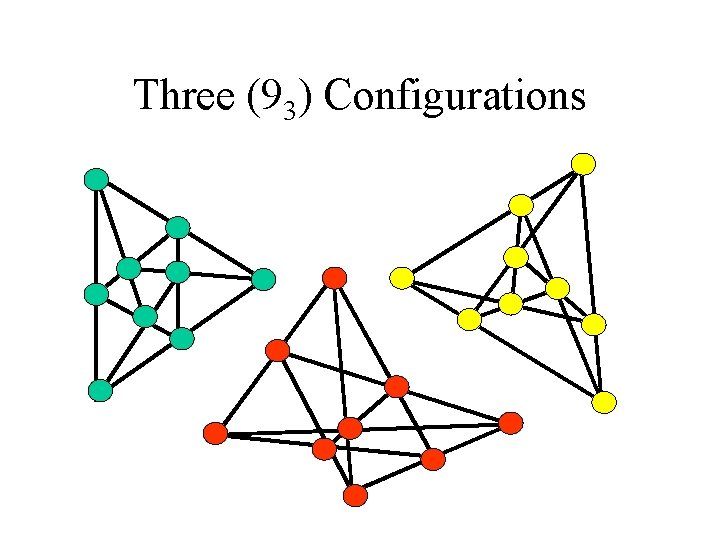
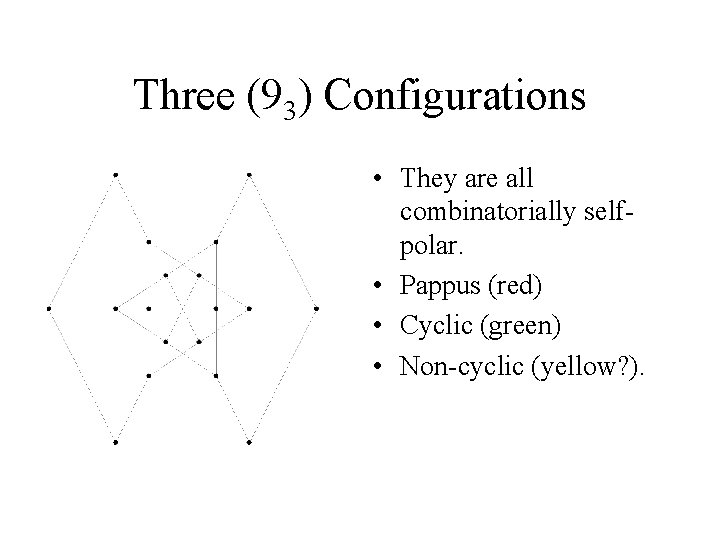
Three (93) Configurations

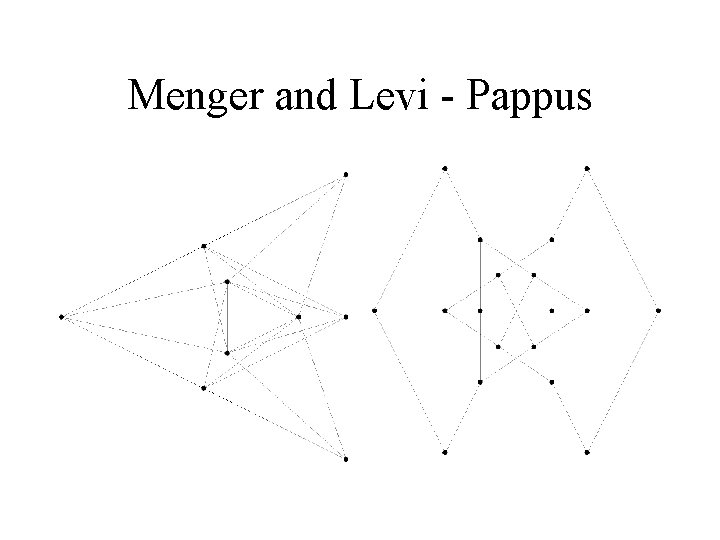
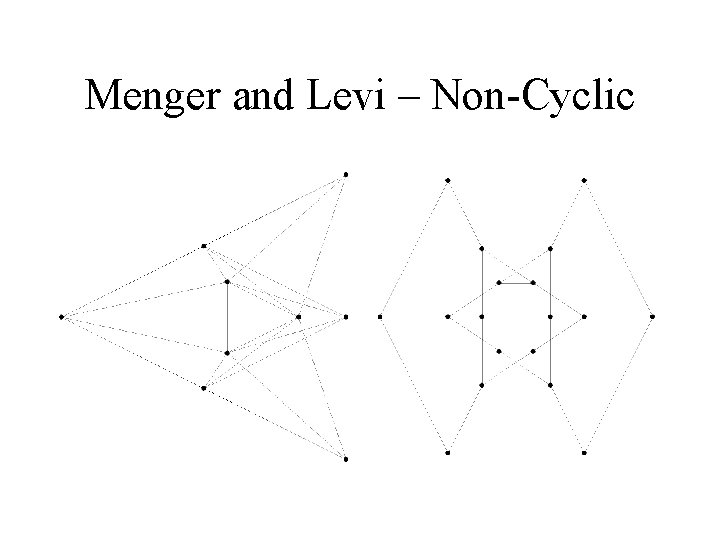
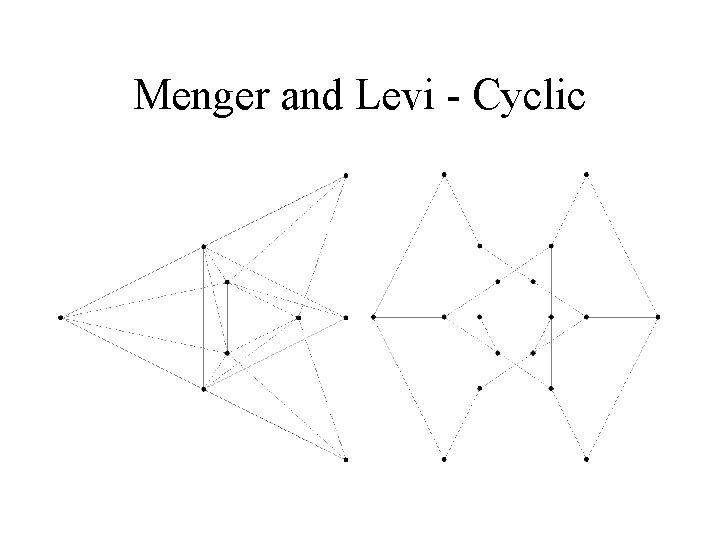
Three (93) Configurations • They are all combinatorially selfpolar. • Pappus (red) • Cyclic (green) • Non-cyclic (yellow? ).

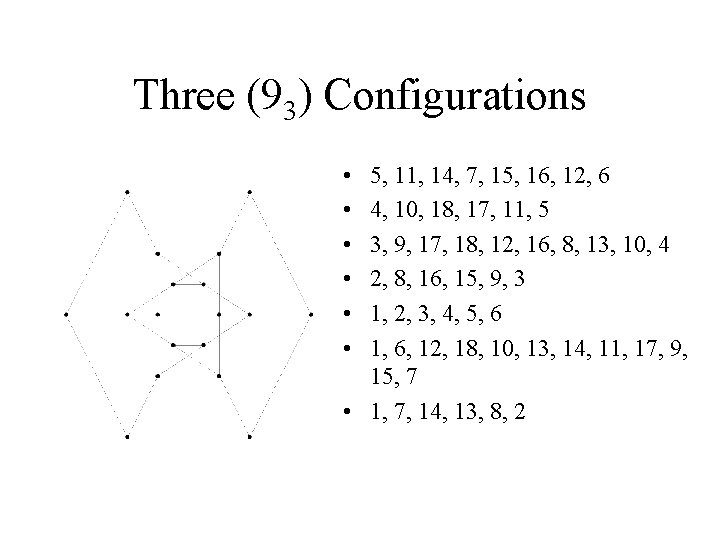
Three (93) Configurations • • • 5, 11, 14, 7, 15, 16, 12, 6 4, 10, 18, 17, 11, 5 3, 9, 17, 18, 12, 16, 8, 13, 10, 4 2, 8, 16, 15, 9, 3 1, 2, 3, 4, 5, 6 1, 6, 12, 18, 10, 13, 14, 11, 17, 9, 15, 7 • 1, 7, 14, 13, 8, 2

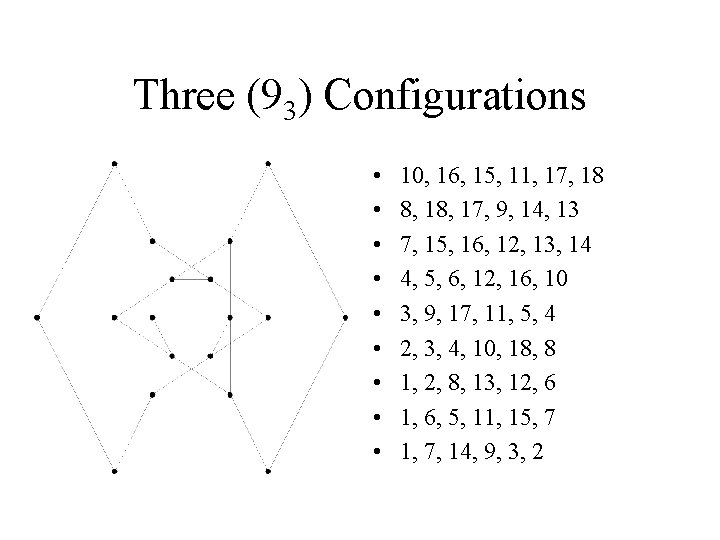
Three (93) Configurations • • • 10, 16, 15, 11, 17, 18 8, 17, 9, 14, 13 7, 15, 16, 12, 13, 14 4, 5, 6, 12, 16, 10 3, 9, 17, 11, 5, 4 2, 3, 4, 10, 18, 8 1, 2, 8, 13, 12, 6 1, 6, 5, 11, 15, 7 1, 7, 14, 9, 3, 2

Exercises • N 1. Show that each (9_3) configuration is combinatorially self-polar. • N 2. Determine the groups of automorphisms and extended automorphisms. • N 3. Show that the genus of two configurations is 1 while the genus of the third one is 2. Make models! • N 4. Determine three Menger graphs and their duals on the minimal surfaces. • N 4. Prove that the complements of the three Menger graphs are respectively C 9, C 6 [ C 3, 3 C 3.

Menger and Levi - Pappus

Menger and Levi – Non-Cyclic

Menger and Levi - Cyclic

Again - Shaken

Menger and Its Complement G(5, 2)

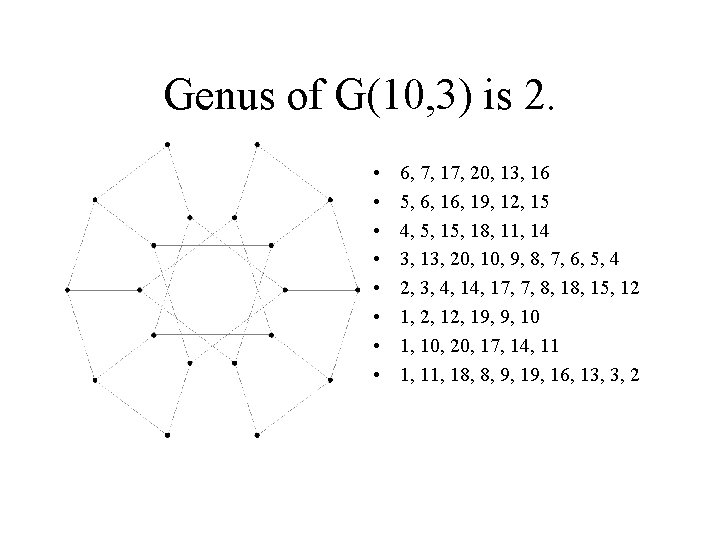
Genus of G(10, 3) is 2. • • 6, 7, 17, 20, 13, 16 5, 6, 19, 12, 15 4, 5, 18, 11, 14 3, 13, 20, 10, 9, 8, 7, 6, 5, 4 2, 3, 4, 17, 7, 8, 15, 12 1, 2, 19, 9, 10 1, 10, 20, 17, 14, 11 1, 18, 8, 9, 16, 13, 3, 2

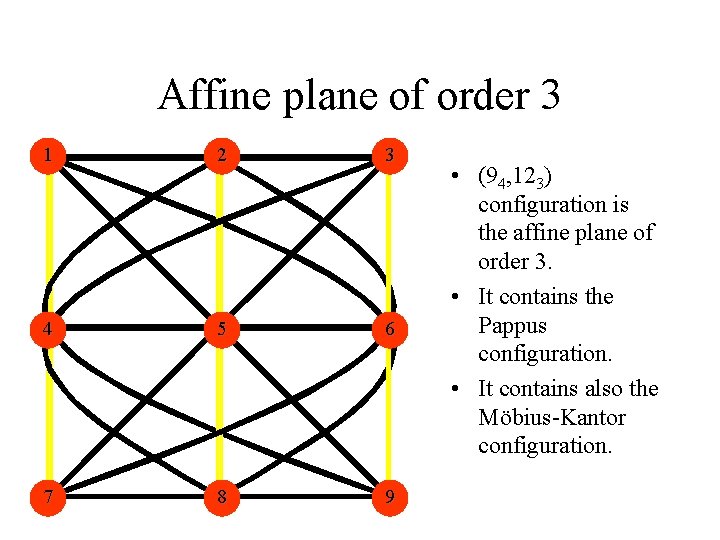
Affine plane of order 3 1 2 3 4 5 6 7 8 9 • (94, 123) configuration is the affine plane of order 3. • It contains the Pappus configuration. • It contains also the Möbius-Kantor configuration.

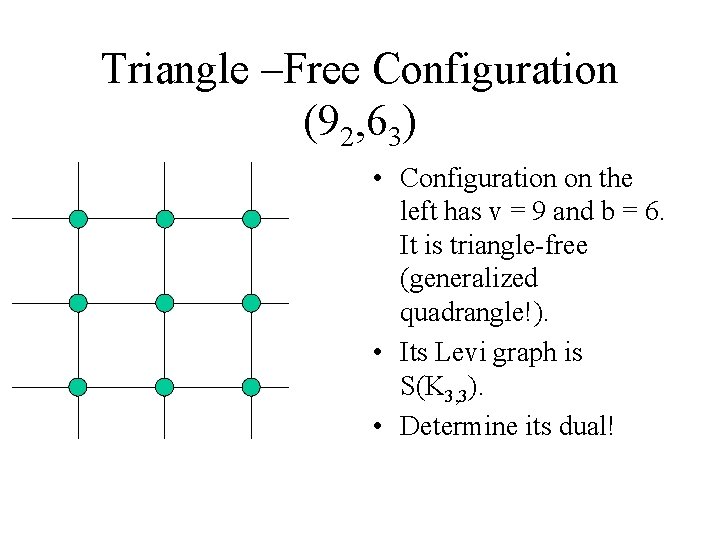
Triangle –Free Configuration (92, 63) • Configuration on the left has v = 9 and b = 6. It is triangle-free (generalized quadrangle!). • Its Levi graph is S(K 3, 3). • Determine its dual!

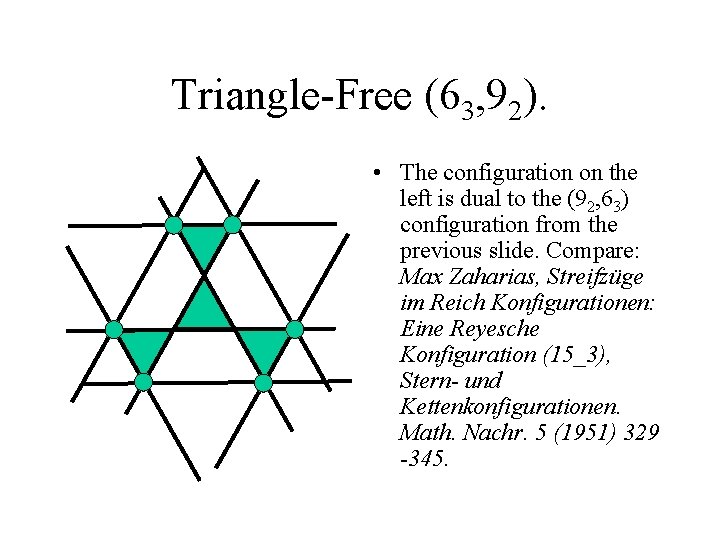
Triangle-Free (63, 92). • The configuration on the left is dual to the (92, 63) configuration from the previous slide. Compare: Max Zaharias, Streifzüge im Reich Konfigurationen: Eine Reyesche Konfiguration (15_3), Stern- und Kettenkonfigurationen. Math. Nachr. 5 (1951) 329 -345.

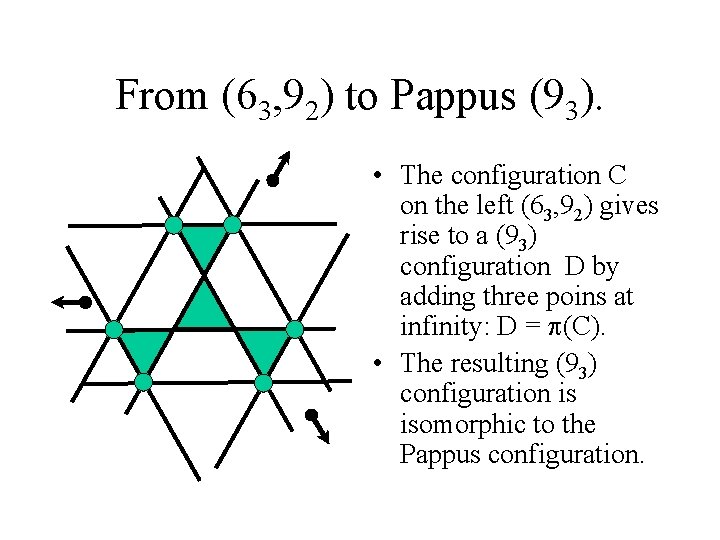
From (63, 92) to Pappus (93). • The configuration C on the left (63, 92) gives rise to a (93) configuration D by adding three poins at infinity: D = p(C). • The resulting (93) configuration is isomorphic to the Pappus configuration.

p(C) • Let C be an arbitrary geometric incidence structure in Euclidean plane. • By p(C) we denote the projective incidence structure obtained from C by adding a point at infinity for each bundle of parallel lines that contains at least two parallel lines. • By pk(C) we denote a similar structure in which we add a point at infinity only if there at least k points on a bundle of parallel lines.

1(C) • Let C be an arbitrary geometric incidence structure in extended Euclidean plane. • By 1(C) we denote the projective incidence structure obtained from C by adding a line at infinity. • 1(C, ax + by + cz = 0) we denote a similar structure (for a configuration in Euclidean 3 space) in which we add a line at infinity defined by the plane ax + by +cz = 0.

Grünbaum configuration calculus • In the previous slides we have learned two operations on geometric incidence structures: p(C) and 1(C). • These ideas can be generalized and the whole system is called Grünbaum configuration calculus as Branko Grünbaum is certainly the main author and promotor of many constructions of this type.

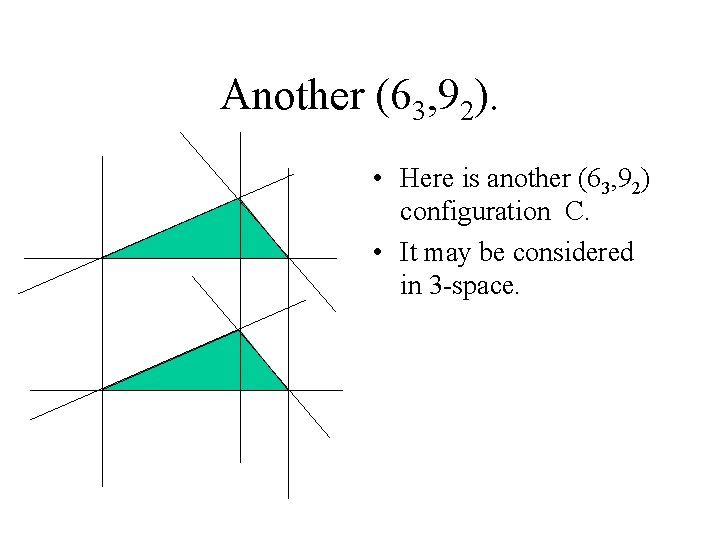
Another (63, 92). • Here is another (63, 92) configuration C. • It may be considered in 3 -space.

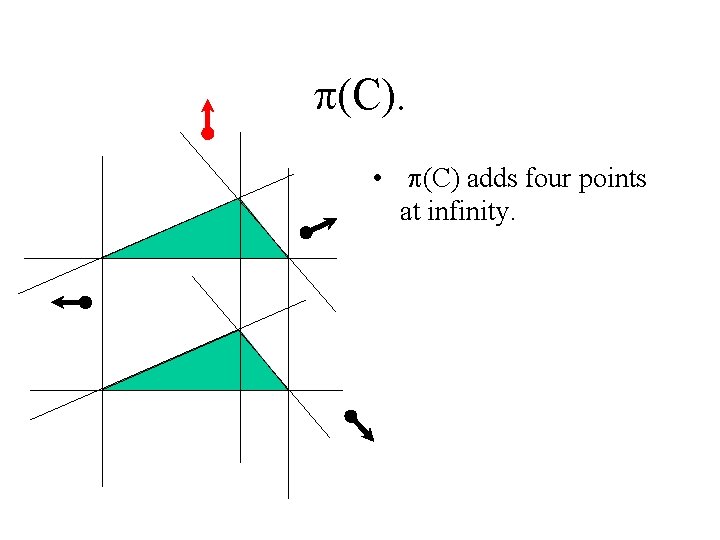
p(C). • p(C) adds four points at infinity.

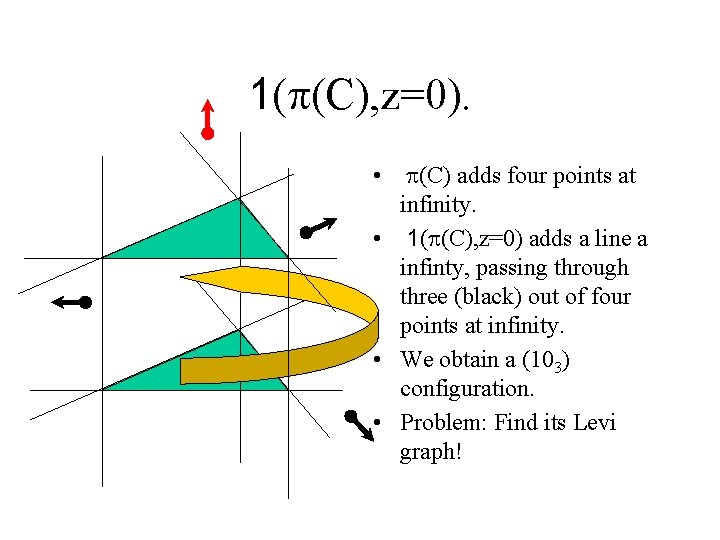
1(p(C), z=0). • p(C) adds four points at infinity. • 1(p(C), z=0) adds a line a infinty, passing through three (black) out of four points at infinity. • We obtain a (103) configuration. • Problem: Find its Levi graph!

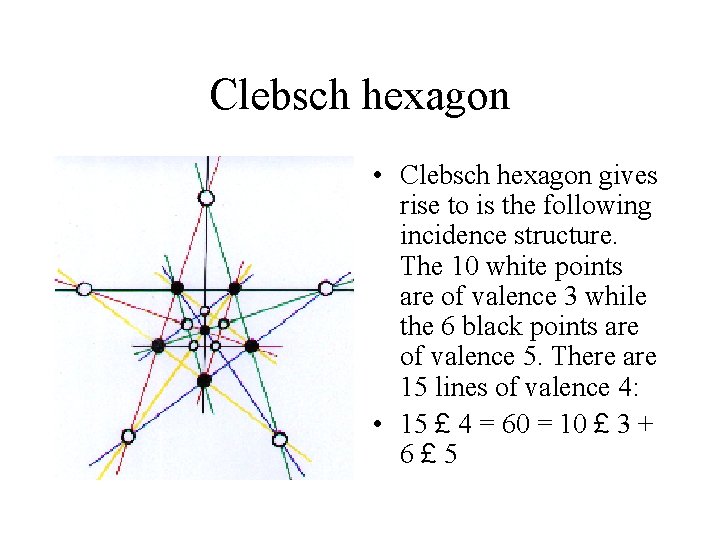
Clebsch hexagon • Clebsch hexagon gives rise to is the following incidence structure. The 10 white points are of valence 3 while the 6 black points are of valence 5. There are 15 lines of valence 4: • 15 £ 4 = 60 = 10 £ 3 + 6£ 5

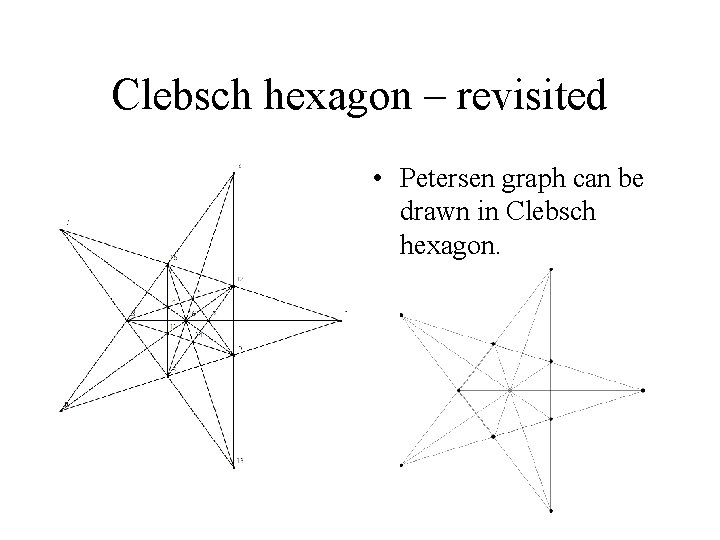
Clebsch hexagon – revisited • Petersen graph can be drawn in Clebsch hexagon.

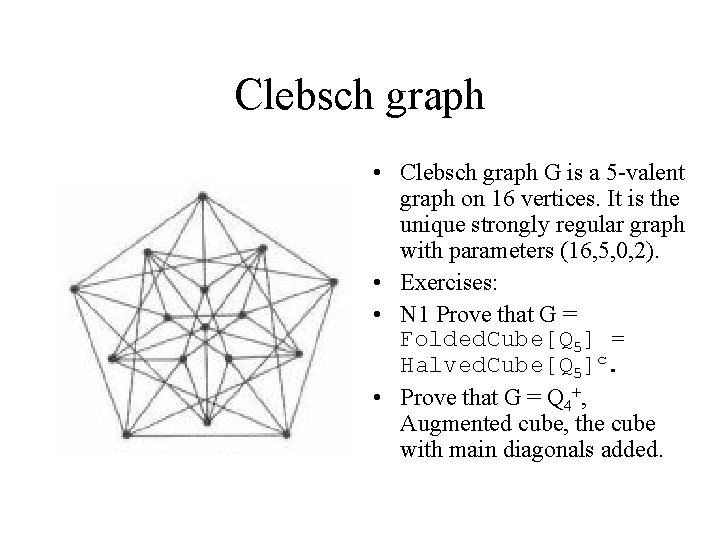
Clebsch graph • Clebsch graph G is a 5 -valent graph on 16 vertices. It is the unique strongly regular graph with parameters (16, 5, 0, 2). • Exercises: • N 1 Prove that G = Folded. Cube[Q 5] = Halved. Cube[Q 5]c. • Prove that G = Q 4+, Augmented cube, the cube with main diagonals added.

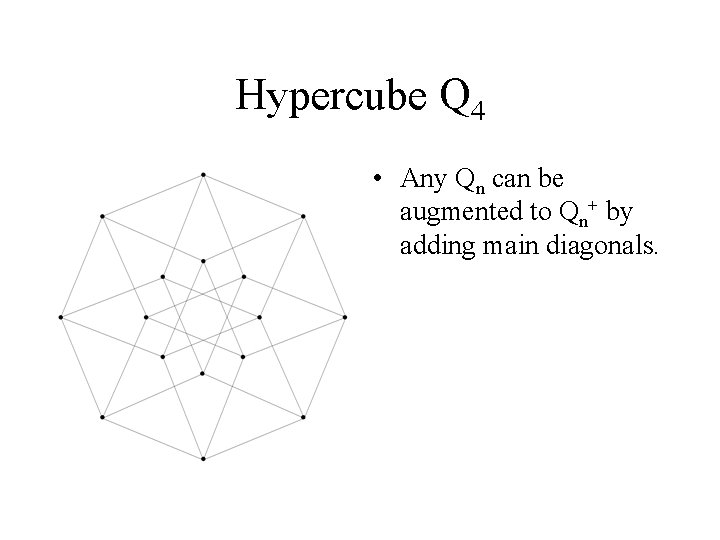
Hypercube Q 4 • Any Qn can be augmented to Qn+ by adding main diagonals.

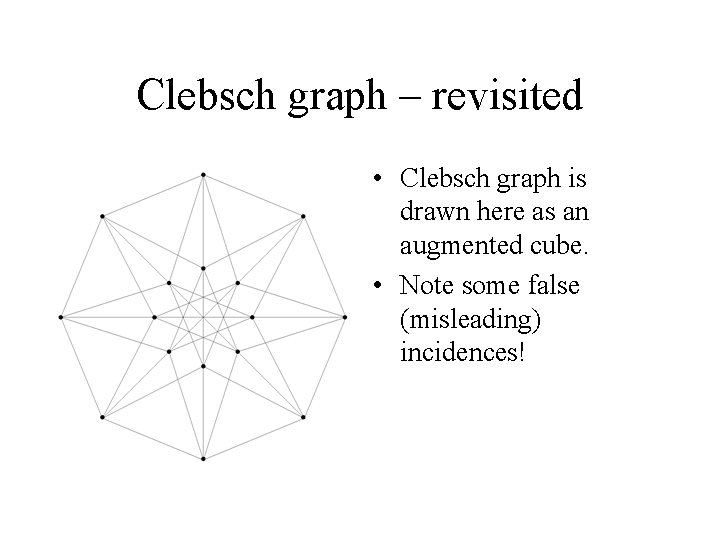
Clebsch graph – revisited • Clebsch graph is drawn here as an augmented cube. • Note some false (misleading) incidences!

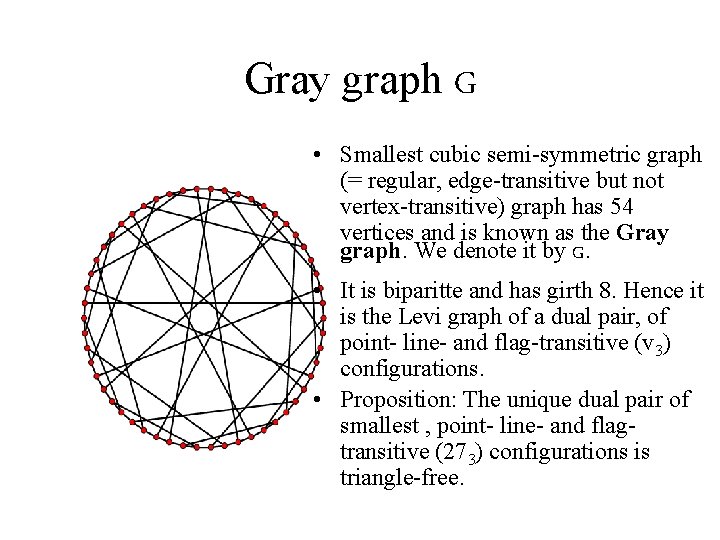
Gray graph G • Smallest cubic semi-symmetric graph (= regular, edge-transitive but not vertex-transitive) graph has 54 vertices and is known as the Gray graph. We denote it by G. • It is biparitte and has girth 8. Hence it is the Levi graph of a dual pair, of point- line- and flag-transitive (v 3) configurations. • Proposition: The unique dual pair of smallest , point- line- and flagtransitive (273) configurations is triangle-free.

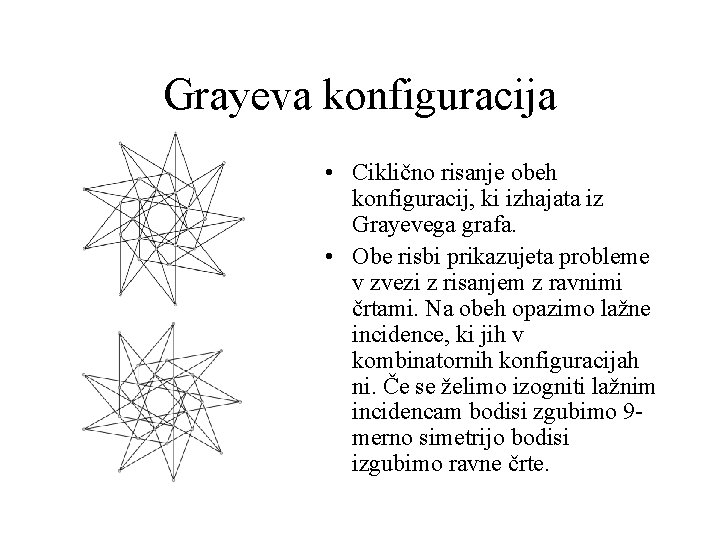
Grayeva konfiguracija • Ciklično risanje obeh konfiguracij, ki izhajata iz Grayevega grafa. • Obe risbi prikazujeta probleme v zvezi z risanjem z ravnimi črtami. Na obeh opazimo lažne incidence, ki jih v kombinatornih konfiguracijah ni. Če se želimo izogniti lažnim incidencam bodisi zgubimo 9 merno simetrijo bodisi izgubimo ravne črte.

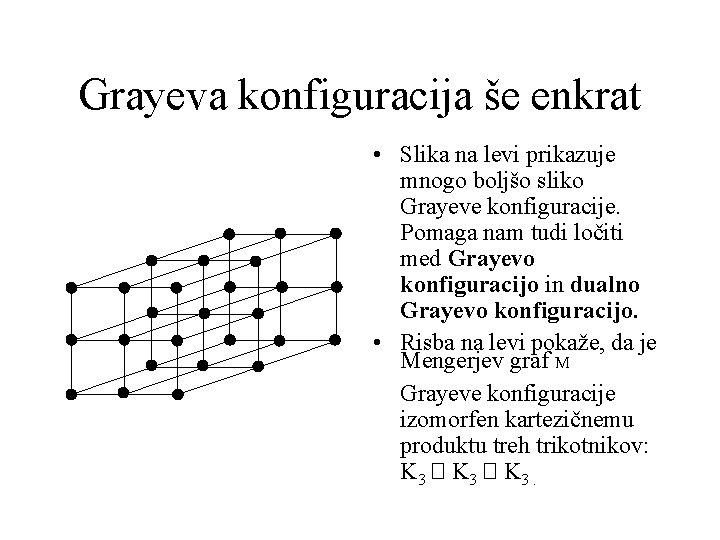
Grayeva konfiguracija še enkrat • Slika na levi prikazuje mnogo boljšo sliko Grayeve konfiguracije. Pomaga nam tudi ločiti med Grayevo konfiguracijo in dualno Grayevo konfiguracijo. • Risba na levi pokaže, da je Mengerjev graf M Grayeve konfiguracije izomorfen kartezičnemu produktu treh trikotnikov: K 3 � K 3.

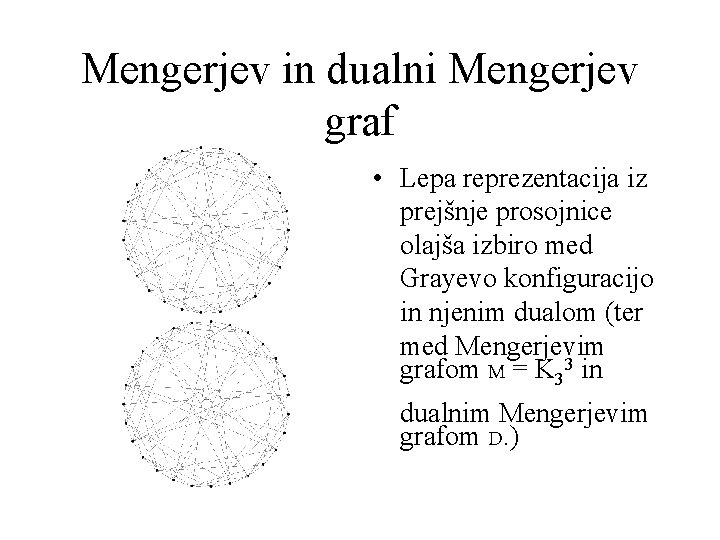
Mengerjev in dualni Mengerjev graf • Lepa reprezentacija iz prejšnje prosojnice olajša izbiro med Grayevo konfiguracijo in njenim dualom (ter med Mengerjevim grafom M = K 33 in dualnim Mengerjevim grafom D. )

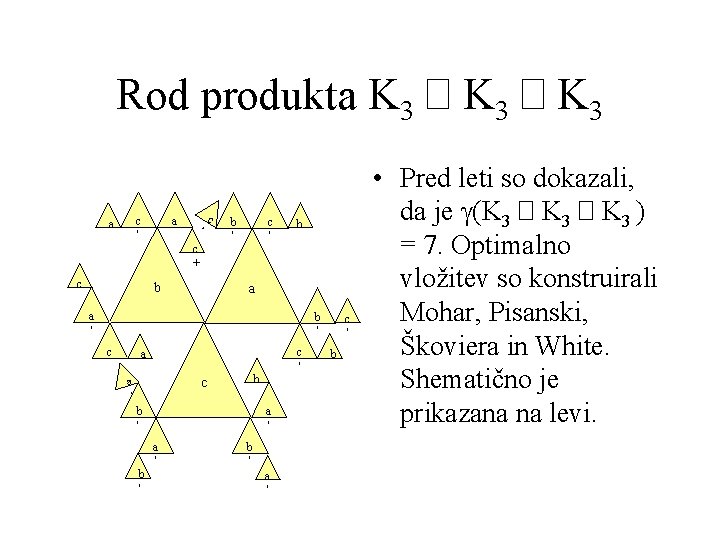
Rod produkta K 3 � K 3 c ' a a ' c c + c b b ' c ' b a a ' b ' c c ' a b c a ' b ' a ' c ' b • Pred leti so dokazali, da je g(K 3 � K 3 ) = 7. Optimalno vložitev so konstruirali Mohar, Pisanski, Škoviera in White. Shematično je prikazana na levi.

Optimalna vložitev • Optimalna vložitev s prejšnje prosojnice ima nekaj zelo lepih lastnosti: – Njen dual je dvodelni. – Vložitev uporabi vseh 27 trikotnikov grafa za lica – Če pobarvamo lica z dvema barvama, je vseh 27 trikotnikov pobarvanih z isto barvo. • Od tod pa sledi zelo pomembna ugotovitev: Točke Grayeve konfiguracije ustrezajo vozliščem, premice pa trikotnikom vložitve. Incidenca je seveda določena s povezavami.

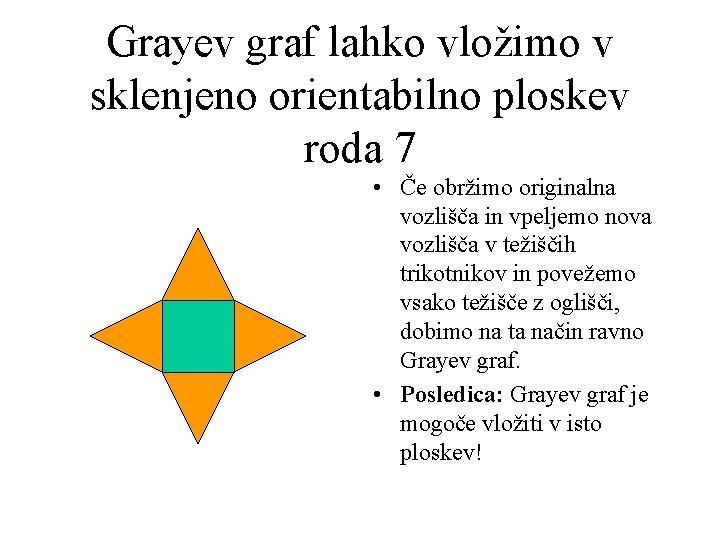
Grayev graf lahko vložimo v sklenjeno orientabilno ploskev roda 7 • Če obržimo originalna vozlišča in vpeljemo nova vozlišča v težiščih trikotnikov in povežemo vsako težišče z oglišči, dobimo na ta način ravno Grayev graf. • Posledica: Grayev graf je mogoče vložiti v isto ploskev!

Grayev graf lahko vložimo v sklenjeno orientabilno ploskev roda 7 • Če obržimo originalna vozlišča in vpeljemo nova vozlišča v težiščih trikotnikov in povežemo vsako težišče z oglišči, dobimo na ta način ravno Grayev graf. • Posledica: Grayev graf je mogoče vložiti v isto ploskev!

Spodnja meja • Zgornja meja je potemtakem 7. Da je tudi spodnja meja 7, sledi iz naslednjega rezultata: • Trditev: Naj bo L Levijev in M Mengerjev graf neke (v 3) konfiguracije C, tedaj velja ocena g(M) g(L). • Dokaz: Začnemo z optimalno vložitvijo grafa L. Že opisani proces lahko obrnemo (in vpeljemo trikotnike). Tako dobimo vložitev grafa M v isto ploskev.

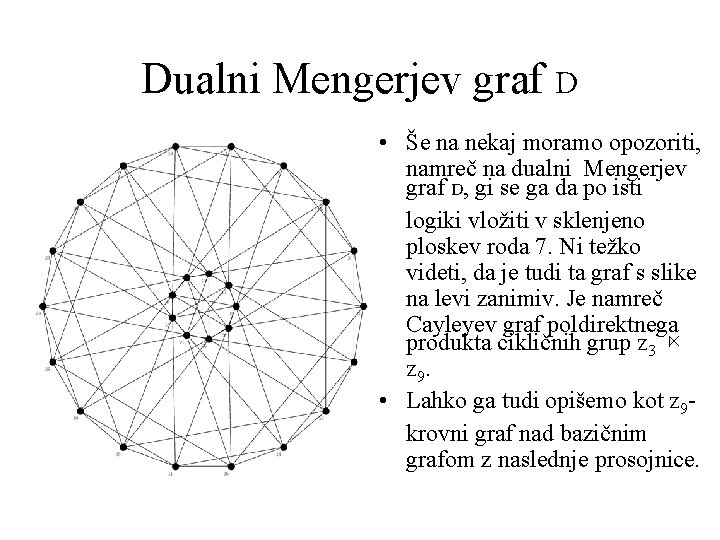
Dualni Mengerjev graf D • Še na nekaj moramo opozoriti, namreč na dualni Mengerjev graf D, gi se ga da po isti logiki vložiti v sklenjeno ploskev roda 7. Ni težko videti, da je tudi ta graf s slike na levi zanimiv. Je namreč Cayleyev graf poldirektnega produkta cikličnih grup Z 3 ⋉ Z 9. • Lahko ga tudi opišemo kot Z 9 krovni graf nad bazičnim grafom z naslednje prosojnice.

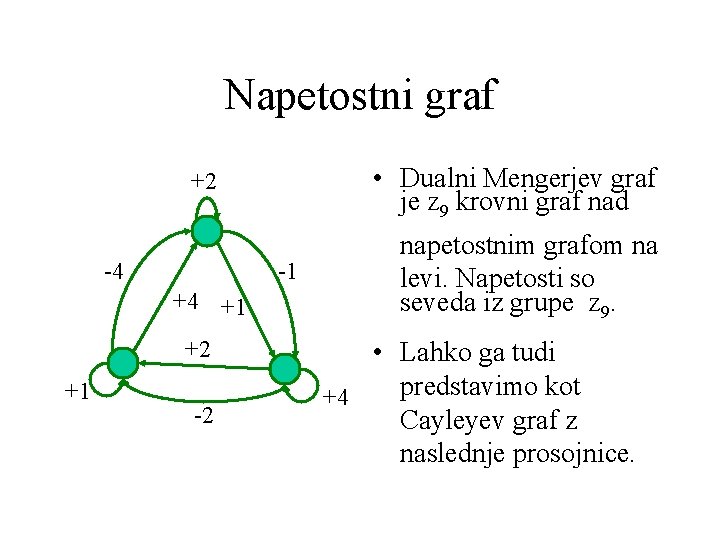
Napetostni graf • Dualni Mengerjev graf je Z 9 krovni graf nad +2 -4 -1 +4 +1 +2 +1 -2 napetostnim grafom na levi. Napetosti so seveda iz grupe Z 9. • Lahko ga tudi predstavimo kot +4 Cayleyev graf z naslednje prosojnice.

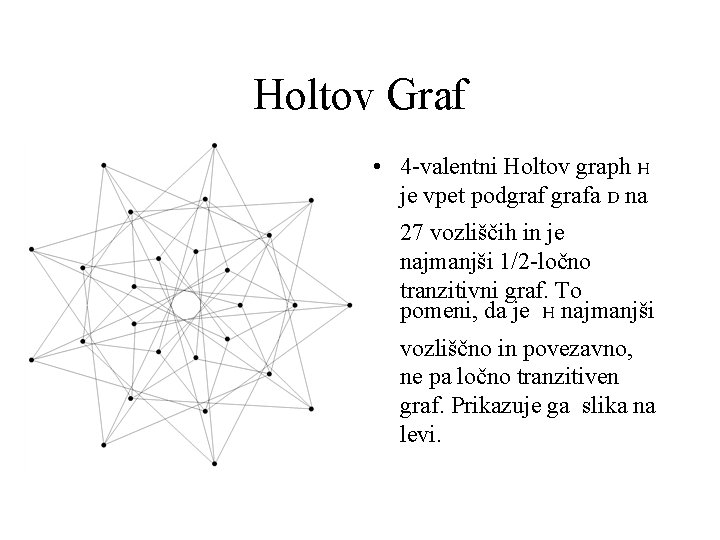
Holtov Graf • 4 -valentni Holtov graph H je vpet podgrafa D na 27 vozliščih in je najmanjši 1/2 -ločno tranzitivni graf. To pomeni, da je H najmanjši vozliščno in povezavno, ne pa ločno tranzitiven graf. Prikazuje ga slika na levi.

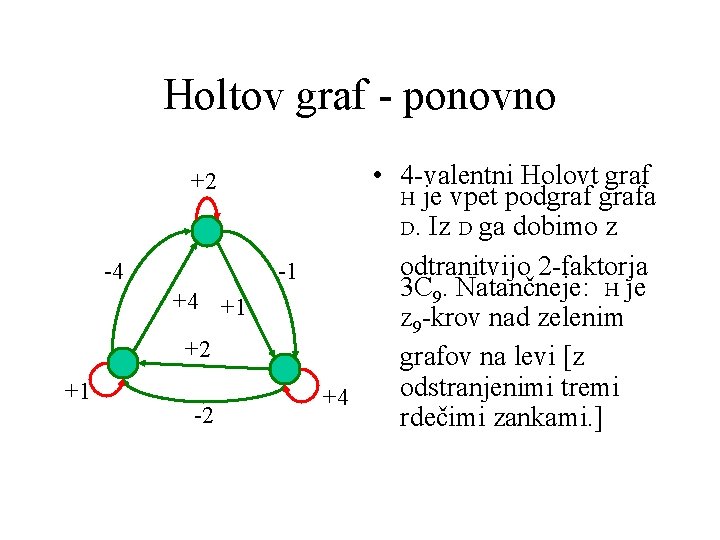
Holtov graf - ponovno +2 -4 +4 +1 +2 +1 -2 • 4 -valentni Holovt graf H je vpet podgrafa D. Iz D ga dobimo z odtranitvijo 2 -faktorja -1 3 C 9. Natančneje: H je Z 9 -krov nad zelenim grafov na levi [z odstranjenimi tremi +4 rdečimi zankami. ]

Nekaj prezentacij grupe Z 3 ⋉ Z 9 • Grafa H in D sta Cayleyeva grafa grupe Z 3 ⋉ Z 9. – Z 3 ⋉ Z 9 = <a, b | a 9 = b 3 = 1, b-1 ab = a 2> – D = <x, y, z | x 9 = y 9 = z 9 = 1, y-1 xy = x 2, y-1 zy = z 2, x-1 yx = y 2, x-1 zx = z 2, z-1 xz = x 2, z -1 yz = y 2> – H dobimo iz D če iz prezentacije odstranimo kateregakoli od x, y, z.

Nerešeni problemi • Kolikšen je rod grafa D? Kolikšen je rod grafa H? Rod grupe Z 3 ⋉ Z 9 je poznan: g(Z 3 ⋉ Z 9) = 4. Po drugi strani smo dokazali, da dopušča D vložitev v sklenjeno ploskev roda 7. Zato velja: – 4 g(D) 7 – 4 g(H) 7 • V prvem primeru bo najbrž lažje izboljšati spodnjo, v drugem pa zgornjo mejo.

Balabanova 10 -kletka • Na levi vidimo Balabanovo 10 kletko. To je najmanjši kubični graf ožine 10. Ima 70 vozlišč, vidimo tudi očitno simetrijo. • Kletka poseduje tudi Hamiltonov cikel. To vidimo npr. iz LCF kode zanjo: • [-9, -25, -19, 29, 13, 35, -13, -29, 19, 25, 9, -29, 17, 33, 21, 9, 13, -31, -9, 25, 17, 9, -31, 27, -9, 17, -19, -29, 27, -17, -9, -29, 33, -25, -21, 17, -17, 29, 35, -29, 17, -17, 21, -25, -33, 29, 9, 17, -27, 29, 19, -17, 9, -27, 31, 9, -17, -25, 9, 31, 13, -9, -21, 33, -17, -29, 29]

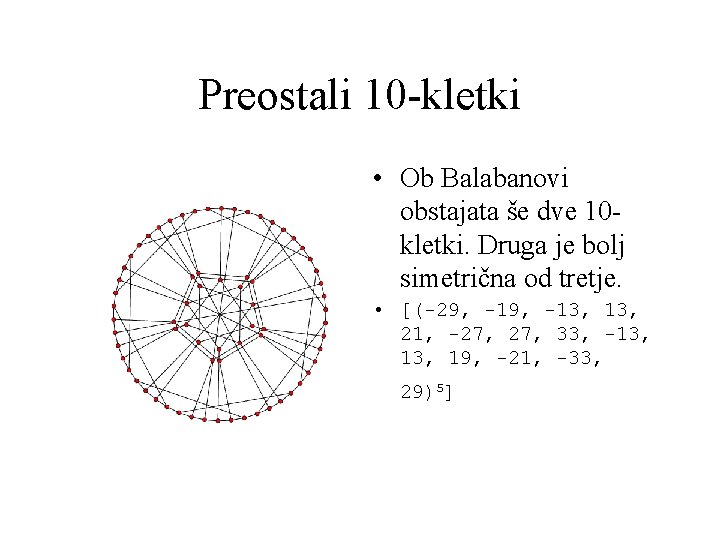
Preostali 10 -kletki • Ob Balabanovi obstajata še dve 10 kletki. Druga je bolj simetrična od tretje. • [(-29, -13, 13, 21, -27, 33, -13, 19, -21, -33, 29)5]

Preostali 10 -kletki • Ob Balabanovi obstajata še dve 10 -kletki. Tretja je najman simetrična. • [9, 25, 31, -17, 33, 9, -29, -15, -9, 9, 25, -25, 29, 17, -9, 9, -27, 35, -9, 9, -17, 21, 27, -29, -9, 25, 13, 19, -33, -17, 19, -31, 27, 11, -25, 29, 33, 13, -13, 21, -29, -21, 25, 9, -11, -19, 29, 9, 27, -19, -13, -35, -9, 9, 17, 25, -9, 9, 27, -27, 21, 15, -9, 29, -29, 33, 9, -25].

10 -kletke • Vse tri 10 -kletke so hamiltonske, zato smo jih lahko opisali z LCF kodo. • Grupe avtomorfizmov imajo rede: 80, 120, 24. • Literatura: T. P. , M. Boben, D. Marušič, A. Orbanič: The 10 -cages and derived Configurations, Discrete Math. 2003 (v tisku).

Exercises • N 1. Prove that G(5, 2) = L(K 5)c.