Algorytmy kodowania ShannonaFano i Huffmana Algorytmy Kompresji Danych

Algorytmy kodowania Shannona-Fano i Huffmana Algorytmy Kompresji Danych wykład 3 Roman Starosolski

Plan wykładu n Algorytm kompresji statystycznej n Algorytm Shannona-Fano n Algorytm Huffmana Rozszerzone kody Huffmana ¨ Dynamiczne kodowanie Huffmana ¨ n Adaptacyjny algorytm kompresji z wykorzystaniem rodziny kodów (Golomb, Golomb-Rice)

Algorytm kompresji statystycznej = = probabilistyczny model danych + + koder entropijny (+ dodatkowe przetwarzanie) (+ dekoder)

Koder entropijny n Koder entropijny to algorytm, którego zadaniem jest, na podstawie znajomości prawdopodobieństw występowania symboli, binarne zakodowanie ciągu symboli tak, aby zminimalizować średnią długość ciągu po zakodowaniu. Z podstawowego twierdzenia Shannona o kodowaniu bezszumowym: LŚr ≥ H(S) gdzie LŚr to średnia długość słowa kodowego kodu przedrostkowego. Zatem dążymy do uzyskania średniej długości słowa kodowego możliwie bliskiej entropii (stąd nazwa „koder entropijny”). n Budowa kodera entropijnego jest banalnie prosta, gdy dysponujemy kodem optymalnym dla rozkładu prawdopodobieństwa symboli źródła

Algorytmy adaptacyjne i inne ¨ algorytm (semi-)statyczny n n stosowany w algorytmach dwuprzebiegowych przebieg 1: analiza stałego ciągu, budowa modelu przebieg 2: kodowanie problemy: ¨ ¨ ¨ dwuprzebiegowy wymaga transmisji i modelu i zakodowanego ciągu algorytm adaptacyjny n n n algorytm jednoprzebiegowy, on-line aktualizacja modelu każdorazowo po zakodowaniu symbolu (taki model nazywamy adaptacyjnym modelem danych) problemy ¨ ¨ przyrostowa aktualizacja modelu nie może być złożona Zero Frequency Problem

Algorytmy adaptacyjne i inne ¨ algorytm stały n budowa dla całej klasy danych n kodowanie przy założeniu, że dane należą do tej klasy n problemy ¨ dane „nie pasujące” do założeń ¨ inne n kilka (stałych) modeli przełączanych adaptacyjnie podczas kodowania n podział ciągu na podciągi i zastosowanie algorytmu statycznego do każdego podciągu z osobna n. . .

„Podstawowe twierdzenie Shannona o kodowaniu bezszumowym” (jedna z postaci twierdzenia, wg. : Drozdek: „Wprowadzenie do kompresji danych”) Dla bezpamięciowego źródła S o entropii H(S) możliwe jest przypisanie ciągom k symboli źródła, słów kodu przedrostkowego tak, że spełnione jest H(S) ≤ Lk / k < H(S) + 1 / k asymptotycznie, możliwe jest uzyskanie średniej długości kodu (w przeliczeniu na pojedynczy symbol) równej entropii źródła ¨ optymalna długość słowa kodowego dla symbolu o prawdopodobieństwie p równa jest –log (p) (czyli autoinformacji dla tego symbolu) ¨ można zbudować koder entropijny o efektywności bliskiej 100% ¨

Jak wygenerować kod przedrostkowy? n Problem: ¨ Mamy wyznaczony przez model rozkład prawdopodobieństwa symboli źródła p 1, p 2, p 3, p 4. . . p. N, : ∑pi = 1 ¨ Znamy optymalne długości słów kodowych (tj. przybliżone długości słów optymalnego kodu przedrostkowego) l 1, l 2, l 3, l 4. . . l. N : li = –log (pi) ¨ Wiemy jaki warunek muszą spełniać długości słów kodowych aby istniał kod jednoznacznie dekodowalny (nierówność Krafta) ∑ 2 -l ≤ 1 i n Chcemy wyznaczyć ¨ Kod przedrostkowy o minimalnej średniej długości kodu n n szukamy: dokładnych długości słów szukamy: postaci (kolejnych bitów) słów

Algorytm Shannona-Fano n Algorytm Shannona-Fano generuje kod przedrostkowy dla zadanego rozkładu prawdopodobieństwa symboli alfabetu.

(na podstawie: A. Drozdek, Wprowadzenie do kompresji danych, WNT, Warszawa, 1999) Krok 1: Ustaw symbole alfabetu źródła w ciąg s uporządkowane zgodnie z prawdopodobieństwem ich użycia; Krok 2: Algorytm. Shannona. Fano(ciąg s) if s zawiera dwa symbole dołącz 0 do słowa kodowego jednego z symboli, 1 do słowa drugiego symbolu; elseif s zawiera więcej niż dwa symbole podziel s na dwa podciągi s 1 i s 2 tak, by różnica między sumą prawdopodobieństw symboli w podciągach była najmniejsza; dołącz 0 do słów kodowych symboli w s 1 i 1 do słów symboli w s 2; Algorytm. Shannona. Fano(s 1); Algorytm. Shannona. Fano(s 2); endif;

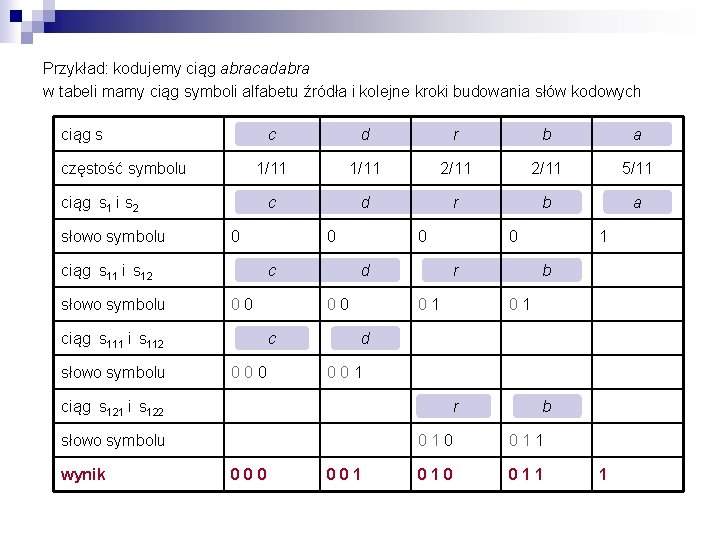
Przykład: kodujemy ciąg abracadabra w tabeli mamy ciąg symboli alfabetu źródła i kolejne kroki budowania słów kodowych ciąg s częstość symbolu c d r b a 1/11 2/11 5/11 c d r b a ciąg s 1 i s 2 słowo symbolu 0 ciąg s 11 i s 12 słowo symbolu c 0 0 ciąg s 111 i s 112 słowo symbolu 0 d 0 0 c 0 0 r 0 1 b 0 1 0 0 1 r słowo symbolu 000 1 d ciąg s 121 i s 122 wynik 0 001 b 0 1 0 0 1 1 010 011 1

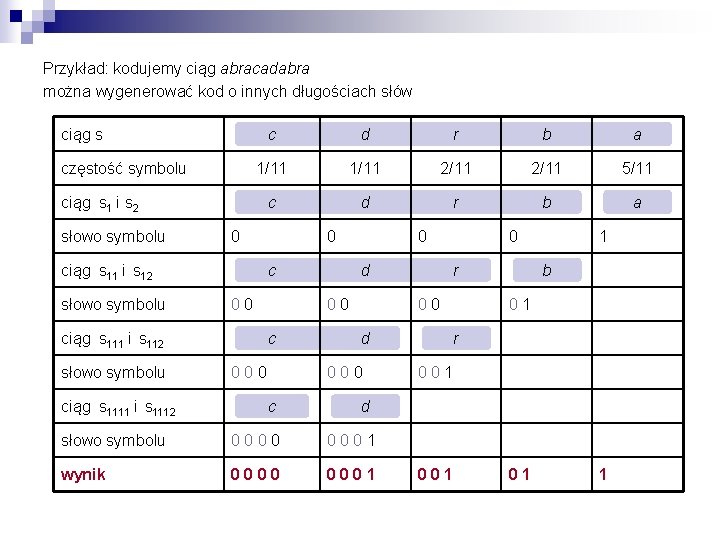
Przykład: kodujemy ciąg abracadabra można wygenerować kod o innych długościach słów ciąg s częstość symbolu c d r b a 1/11 2/11 5/11 c d r b a ciąg s 1 i s 2 słowo symbolu 0 ciąg s 11 i s 12 słowo symbolu c 0 0 ciąg s 111 i s 112 słowo symbolu ciąg s 1111 i s 1112 0 0 d 0 0 c 0 0 0 r 0 0 d 0 0 0 c 0 1 b 0 1 r 0 0 1 d słowo symbolu 0 0 0 0 1 wynik 0000 0001 01 1

Algorytm Huffmana n Algorytm Huffmana generuje kod przedrostkowy dla zadanego rozkładu prawdopodobieństwa symboli alfabetu.

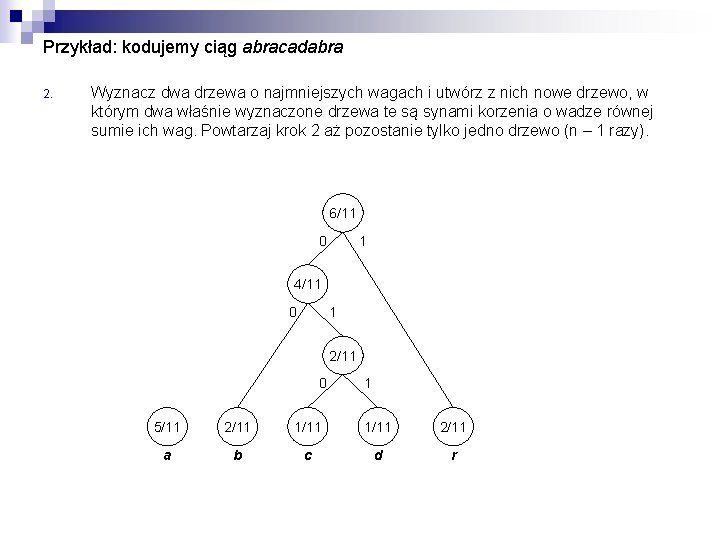
n W algorytmie Huffmana buduje się drzewo binarne, zwane drzewem Huffmana. ¨ ¨ Każdemu z liści odpowiada pojedynczy symbol alfabetu źródła. Z każdym węzłem skojarzona jest waga równa łącznemu prawdopodobieństwu liści w poddrzewie dla którego ten węzeł jest korzeniem 1. Utwórz n drzew, gdzie n jest rozmiarem alfabetu źródła. Każdemu z symboli alfabetu źródła odpowiada pojedyncze drzewo składające się wyłącznie z korzenia i mające wagę równą prawdopodobieństwu wystąpienia danego symbolu. 2. Wyznacz dwa drzewa o najmniejszych wagach i utwórz z nich nowe drzewo, w którym dwa właśnie wyznaczone drzewa te są synami korzenia o wadze równej sumie ich wag. Powtarzaj krok 2 aż pozostanie tylko jedno drzewo (n – 1 razy). 3. Słowo kodowe kodu Huffmana dla danego symbolu znajduje się przechodząc ścieżką od korzenia drzewa Huffmana do liścia odpowiadającego temu symbolowi (i-ty bit słowa kodowego ma wartość 0, jeżeli i-ta krawędź ścieżki prowadzi do lewego syna itego węzła, a 1 — jeżeli do prawego).

Przykład: kodujemy ciąg abracadabra 1. Utwórz n drzew, gdzie n jest rozmiarem alfabetu źródła. Każdemu z symboli alfabetu źródła odpowiada pojedyncze drzewo składające się wyłącznie z korzenia i mające wagę równą prawdopodobieństwu wystąpienia danego symbolu. 5/11 2/11 1/11 2/11 a b c d r

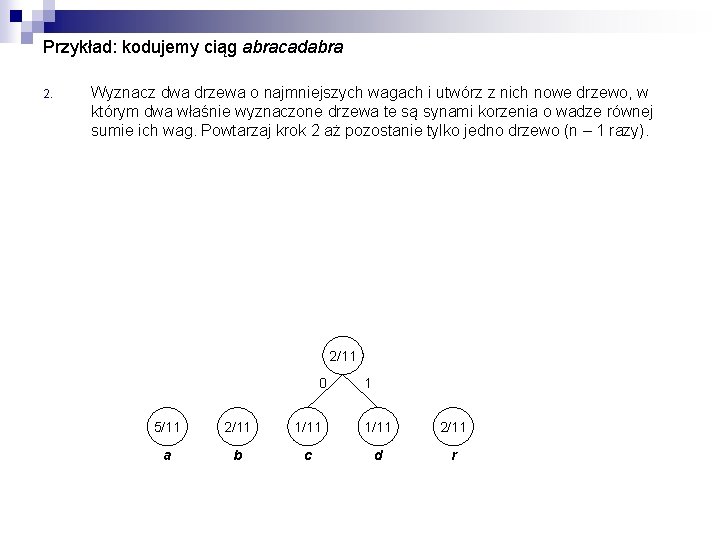
Przykład: kodujemy ciąg abracadabra 2. Wyznacz dwa drzewa o najmniejszych wagach i utwórz z nich nowe drzewo, w którym dwa właśnie wyznaczone drzewa te są synami korzenia o wadze równej sumie ich wag. Powtarzaj krok 2 aż pozostanie tylko jedno drzewo (n – 1 razy). 2/11 0 1 5/11 2/11 1/11 2/11 a b c d r

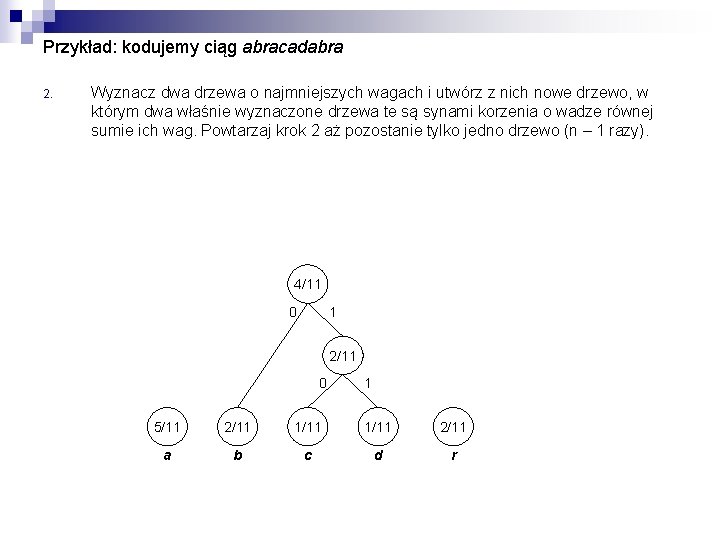
Przykład: kodujemy ciąg abracadabra 2. Wyznacz dwa drzewa o najmniejszych wagach i utwórz z nich nowe drzewo, w którym dwa właśnie wyznaczone drzewa te są synami korzenia o wadze równej sumie ich wag. Powtarzaj krok 2 aż pozostanie tylko jedno drzewo (n – 1 razy). 4/11 0 1 2/11 0 1 5/11 2/11 1/11 2/11 a b c d r

Przykład: kodujemy ciąg abracadabra 2. Wyznacz dwa drzewa o najmniejszych wagach i utwórz z nich nowe drzewo, w którym dwa właśnie wyznaczone drzewa te są synami korzenia o wadze równej sumie ich wag. Powtarzaj krok 2 aż pozostanie tylko jedno drzewo (n – 1 razy). 6/11 0 1 4/11 0 1 2/11 0 1 5/11 2/11 1/11 2/11 a b c d r

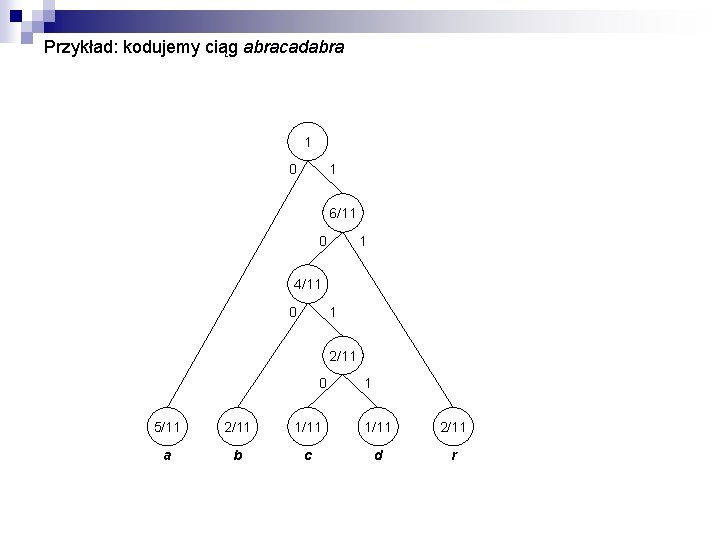
Przykład: kodujemy ciąg abracadabra 1 0 1 6/11 0 1 4/11 0 1 2/11 0 1 5/11 2/11 1/11 2/11 a b c d r

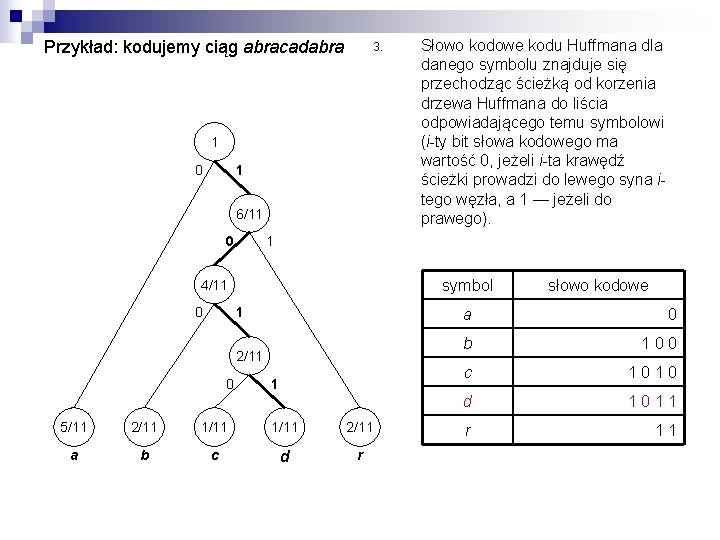
Przykład: kodujemy ciąg abracadabra 3. 1 0 1 6/11 0 1 symbol 4/11 0 1 2/11 0 Słowo kodowe kodu Huffmana dla danego symbolu znajduje się przechodząc ścieżką od korzenia drzewa Huffmana do liścia odpowiadającego temu symbolowi (i-ty bit słowa kodowego ma wartość 0, jeżeli i-ta krawędź ścieżki prowadzi do lewego syna itego węzła, a 1 — jeżeli do prawego). 1 5/11 2/11 1/11 2/11 a b c d r słowo kodowe a 0 b 1 0 0 c 1 0 d 1 0 1 1 r 1 1

Własności kodów Huffmana n Podobnie, jak algorytm Shannona-Fano, przedstawiony algorytm jest niedeterministyczny niedeterminizm można łatwo usunąć – kanoniczne kodowanie Huffmana ¨ n Efektywnośc kodów Huffmana jest typowo nieznacznie większa niż Shannona-Fano (dla przykładu „abracadabra” jest taka sama) algorytm Huffmana jest prostszy ¨ ¨ symbol Shannon-Fano (1) Shannon-Fano (2) Huffman a 1 1 0 b 0 1 1 0 0 c 0 0 0 0 1 0 d 0 0 1 0 0 0 1 1 r 0 1 0 0 0 1 1 1

Własności kodów Huffmana n Kod wygenerowany algorytmem Huffmana jest optymalny w klasie kodów przedrostkowych (gdy prawdopodobieństwa symboli są 2 -N, gdzie N jest nieujemną liczbą całkowitą, to kod jest optymalny, gdyż dla symbolu o prawdopodobieństwie p optymalna długość słowa kodowego to –log (p) bitów) n Nieefektywność kodu Huffmana ¨ Jednocześnie nieefektywność kodów przedrostkowych pmax to prawdopodobieństwo najbardziej prawdopodobnego symbolu.

Rozszerzone kody Huffmana n Kod Huffmana jest nieefektywny, gdy prawdopodobieństwo wystąpienia jednego z symboli jest duże, najbardziej gdy bliskie 1. ¨ ¨ ¨ długość słowa kodowego tego symbolu wynosi 1 bit optymalna długość słowa kodowego jest bliska 0 zatem średnia długość kodu jest wielokrotnie większa od entropii rozkładu prawdopodobieństwa symboli.

„Podstawowe twierdzenie Shannona o kodowaniu bezszumowym” (jedna z postaci twierdzenia, wg. : Drozdek: „Wprowadzenie do kompresji danych”) Dla bezpamięciowego źródła S o entropii H(S) możliwe jest przypisanie ciągom k symboli źródła, słów kodu przedrostkowego tak, że spełnione jest H(S) ≤ Lk / k < H(S) + 1 / k asymptotycznie, możliwe jest uzyskanie średniej długości kodu (w przeliczeniu na pojedynczy symbol) równej entropii źródła ¨ optymalna długość słowa kodowego dla symbolu o prawdopodobieństwie p równa jest –log (p) (czyli autoinformacji dla tego symbolu) ¨ można zbudować koder entropijny o efektywności bliskiej 100% ¨

Rozszerzone kody Huffmana n Kod Huffmana jest nieefektywny, gdy prawdopodobieństwo wystąpienia jednego z symboli jest duże, najbardziej gdy bliskie 1. ¨ ¨ ¨ n długość słowa kodowego tego symbolu wynosi 1 bit optymalna długość słowa kodowego jest bliska 0 zatem średnia długość kodu jest wielokrotnie większa od entropii rozkładu prawdopodobieństwa symboli. Zamiast konstruować kod dla symboli alfabetu źródła możemy zinterpretować kodowany ciąg jako ciąg nad rozszerzonym alfabetem zawierającym ciągi symboli alfabetu źródła

Przykład: Rozszerzone kody Huffmana Kodujemy ciąg binarny (alfabet źródła to {0, 1}) Prawdopodobieństwo wygenerowania zera przez źródło wynosi 0. 9 Entropia rozkładu prawdopodobieństwa H(S) wynosi 0. 467. Efektywność kodu Huffmana dla tego źródła wynosi EHuff. Bin=( H(S)/LHuff. Bin ) • 100%=47% Jeżeli kodować będziemy pary symboli. . . ciąg p(ciąg) słowo kodowe 00 0. 81 0 01 0. 09 10 10 0. 09 110 11 0. 01 111 . . . to średnia długość słowa kodowego (w przeliczeniu na symbol alfabetu źródła) wyniesie 0. 649, czyli efektywność kodu wzrośnie do około 72 %.

Algorytm kompresji z kodowaniem Huffmana n Typowe zastosowanie algorytmu Huffmana (i Shannona-Fano) to statyczny algorytm kompresji. ¨ zbudowanie modelu wymaga znajomości rozkładu prawdopodobieństwa symboli źródła, praktycznie przesyła się tablicę częstości wystąpień symboli ¨ koszt transmisji modelu np. dla alfabetu źródła ASCII jest niewielki ¨ kodowanie jest bardzo szybkie n n po zbudowaniu modelu wyliczamy słowa kodowe wszystkich symboli alfabetu źródła kodowanie polega na wyprowadzeniu już wyliczonych słów kodowych dla kolejnych symboli kodowanego ciąg

Algorytm kompresji z kodowaniem Huffmana n Zalety ¨ prosty ¨ szybki n wady ¨ nieefektywny gdy prawdopodobieństwo wystąpienia jednego z symboli alfabetu źródła jest duże (ale można kodować ciągi symboli) ¨ dwuprzebiegowy n n koszt transmisji modelu może być duży nie do zastosowania wprost do kodowania on-line

Dynamiczne kodowanie Huffmana n Użycie algorytmu Huffmana w adaptacyjnym modelu jest możliwe Metoda brute-force – każdorazowo po zakodowniu symbolu buduj od nowa drzewo Huffmana ( Uwaga na Zero Frequency Problem ). . . ale w praktyce zbyt kosztowne

Dynamiczne kodowanie Huffmana n Algorytmy Dynamicznego kodowania Huffmana ¨ n To algorytm generujący kod zbliżony do kodu Huffmana, nadający się do zastosowania w algorytmie adaptacyjnym ¨ n n n (Adaptacyjne kodowanie Huffmana) Drzewo Huffmana budowane jest przyrostowo – możliwa jest „aktualizacja modelu” Ww. algorytm został wynaleziony niezależnie przez Fallera i Gallagera. . . udoskonalony przez Cormacka i Horspoola oraz (niezależnie) przez Knutha. . . następnie udoskonalony przez Vittera

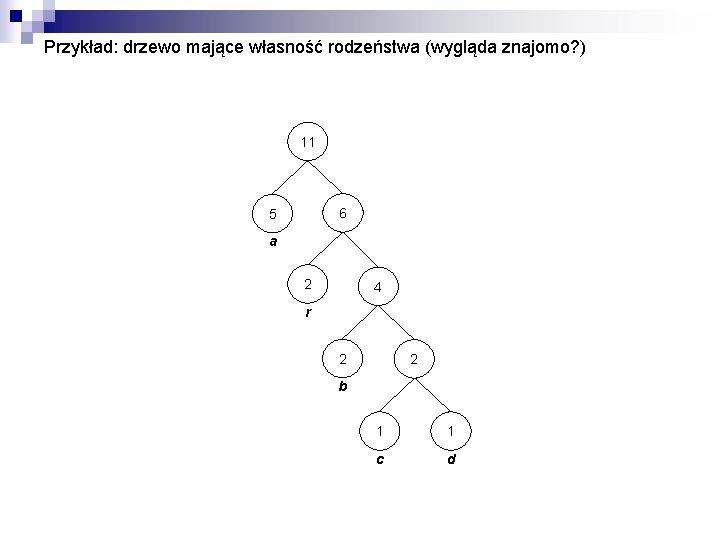
Algorytm Fallera-Gallagera n Budujemy przyrostowo drzewo binarne, którego węzły zawierają liczniki częstości, a liście są dodatkowo skojarzone z symbolami alfabetu źródła n Drzewo ma własność rodzeństwa gdy: 1. 2. n każdy węzeł nie będący liściem ma 2 potomków przechodząc węzły w kolejności z góry do dołu, a na danym poziomie od prawej do lewej, otrzymamy ciąg węzłów o nierosnących licznikach Drzewo mające własność rodzeństwa jest drzewem Huffmana (tw. Fallera-Gallagera)

Przykład: drzewo mające własność rodzeństwa (wygląda znajomo? ) 11 6 5 a 2 4 r 2 2 b 1 1 c d

Algorytm Fallera-Gallagera n Budowane drzewo zawiera liść (0 -węzeł) reprezentujący wszystkie symbole, które jeszcze nie wystąpiły w kodowanym ciągu n Kodowanie rozpoczynamy od drzewa składającego się wyłącznie z 0 -węzła n Używamy pomocniczej struktury węzły, listy dwukierunkowej zawierającej węzły drzewa uporządkowane w kolejności przeglądania drzewa z góry do dołu, a na danym poziomie od prawej do lewej n Podlistę listy węzły składającą się z wszystkich węzłów o wartości licznika i nazywamy blokiem-i , a pierwszy węzeł takiego bloku liderem

(na podstawie: A. Drozdek, Wprowadzenie do kompresji danych, WNT, Warszawa, 1999) Dynamiczne. Kodowanie. Huffmana. FGK(symbol s) p = liść zawierający symbol s; wyprowadź słowo kodowe dla s (*); if p jest 0 -węzłem utwórz nowy węzeł q dla symolu s; q. licznik = 1; p = nowy węzeł w miejscu 0 -węzła będący rodzicem 0 -węzła i węzła q; p. licznik = 1; else p. licznik++; endif while p nie jest korzeniem if p narusza własność rodzeństwa if lider bloku-i zawierającego p nie jest rodzicem p zamień p z liderem; endif p = rodzic(p); p. licznik++; endwhile

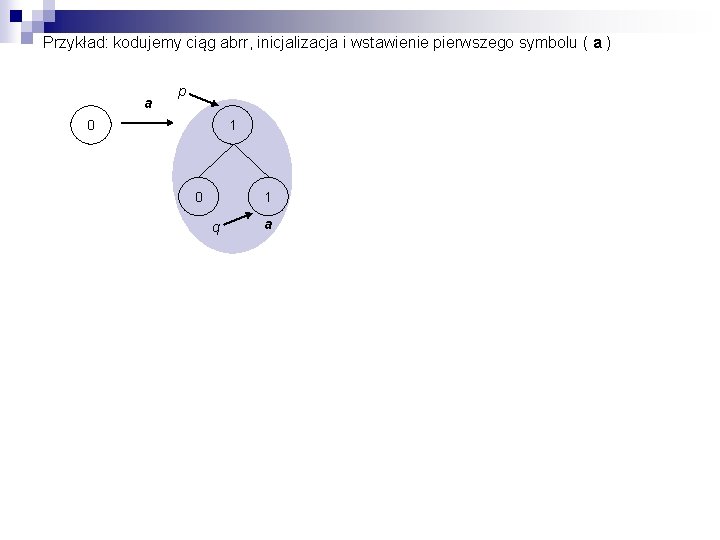
Przykład: kodujemy ciąg abrr, inicjalizacja i wstawienie pierwszego symbolu ( a ) a p 0 1 q a

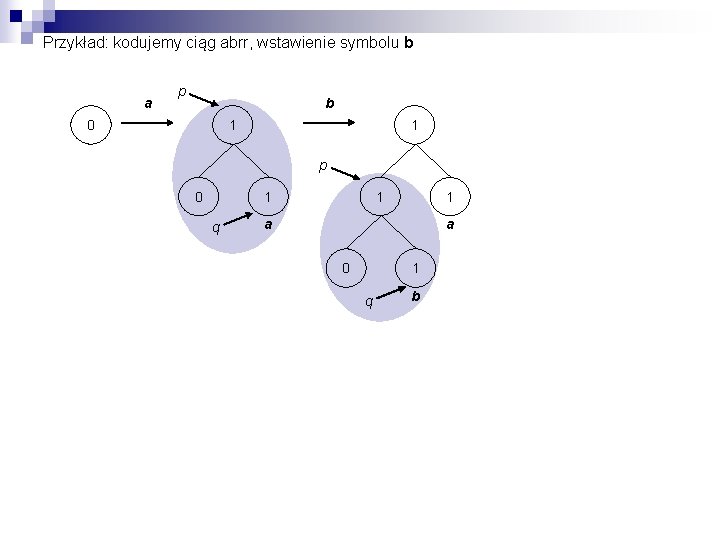
Przykład: kodujemy ciąg abrr, wstawienie symbolu b a p b 0 1 1 p 0 1 1 q 1 a a 0 1 q b

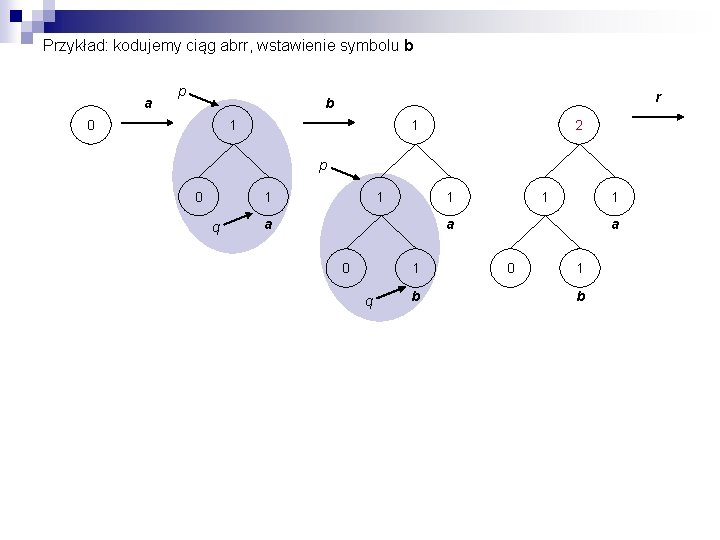
Przykład: kodujemy ciąg abrr, wstawienie symbolu b a p r b 0 1 1 2 p 0 1 1 q 1 1 a 0 1 q b a 0 1 b

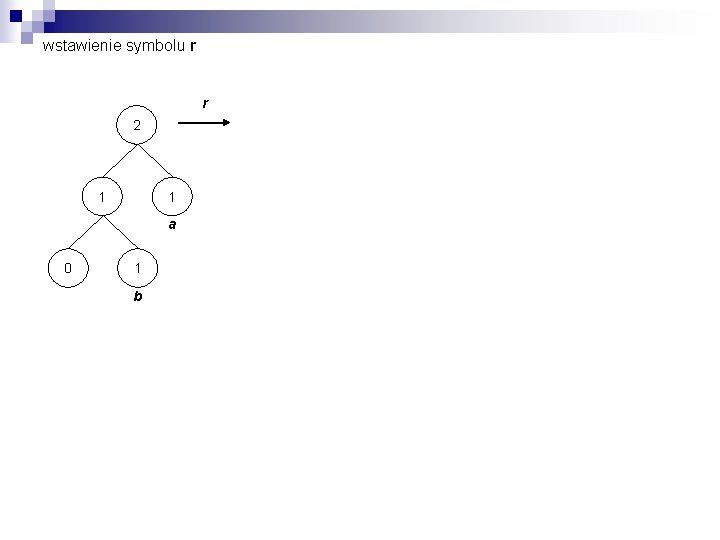
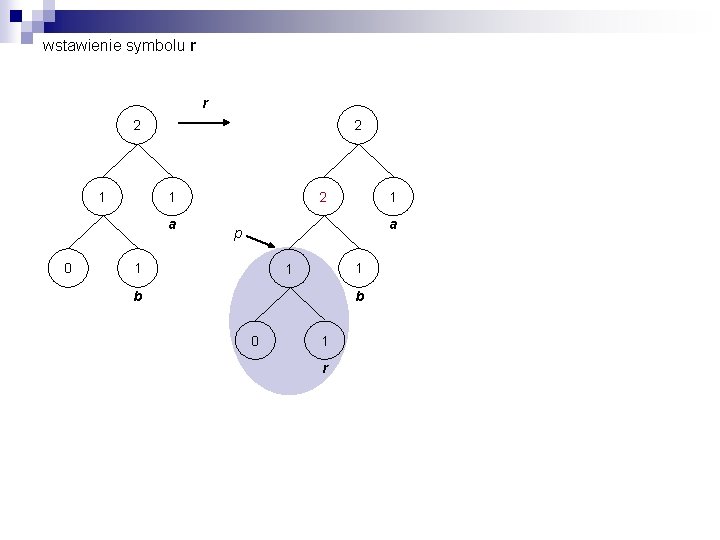
wstawienie symbolu r r 2 1 1 a 0 1 b

wstawienie symbolu r r 2 1 2 a 0 2 1 1 a p 1 1 1 b b 0 1 r

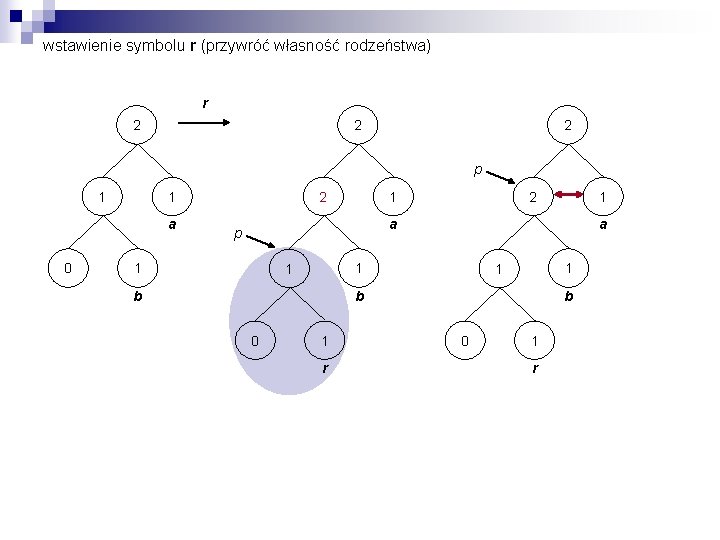
wstawienie symbolu r (przywróć własność rodzeństwa) r 2 2 2 p 1 a 0 2 1 1 a p 1 a 1 1 b 0 1 r

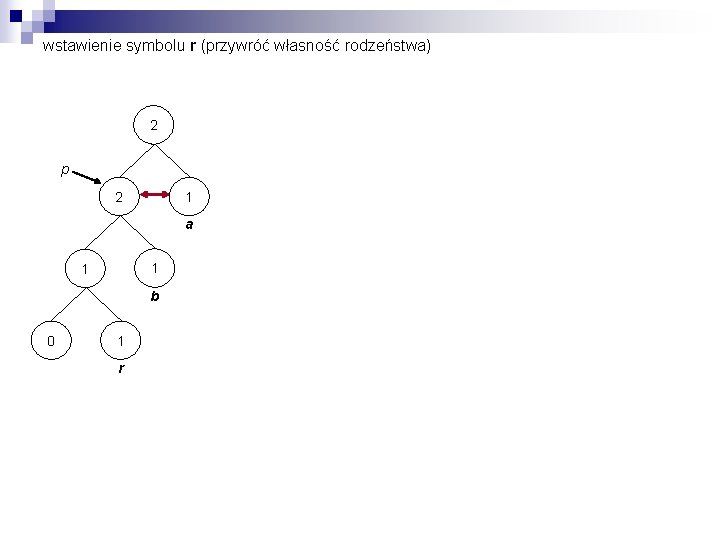
wstawienie symbolu r (przywróć własność rodzeństwa) 2 p 2 1 a 1 1 b 0 1 r

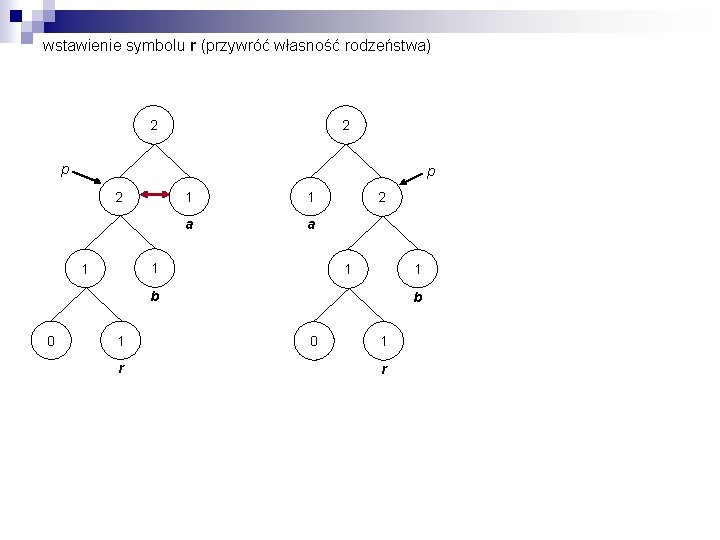
wstawienie symbolu r (przywróć własność rodzeństwa) 2 2 p p 2 1 1 a a 1 1 2 1 1 b 0 1 r

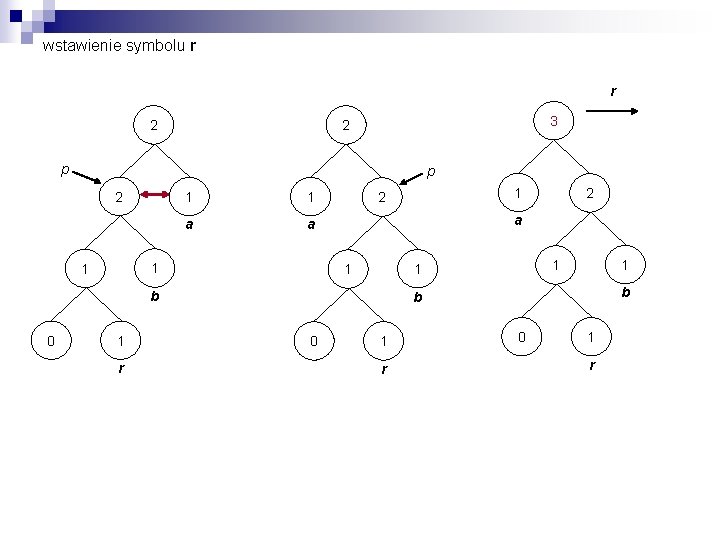
wstawienie symbolu r r 2 3 2 p p 2 1 1 a a 1 1 1 r 2 a 1 1 b 0 1 2 b b 0 1 r

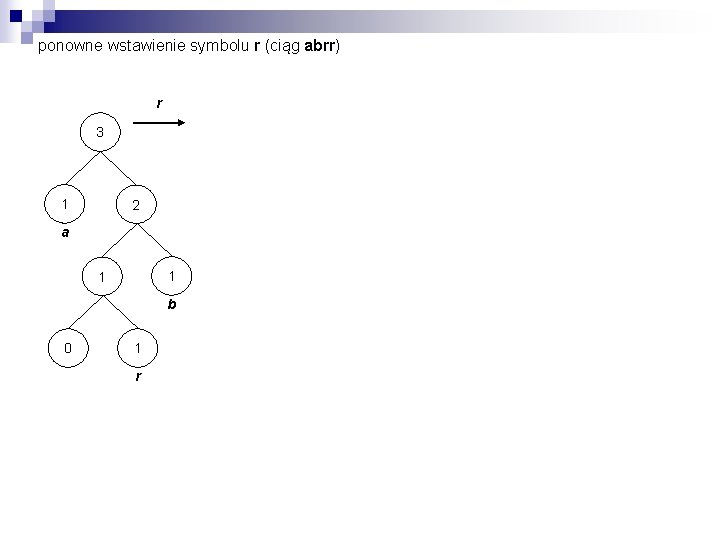
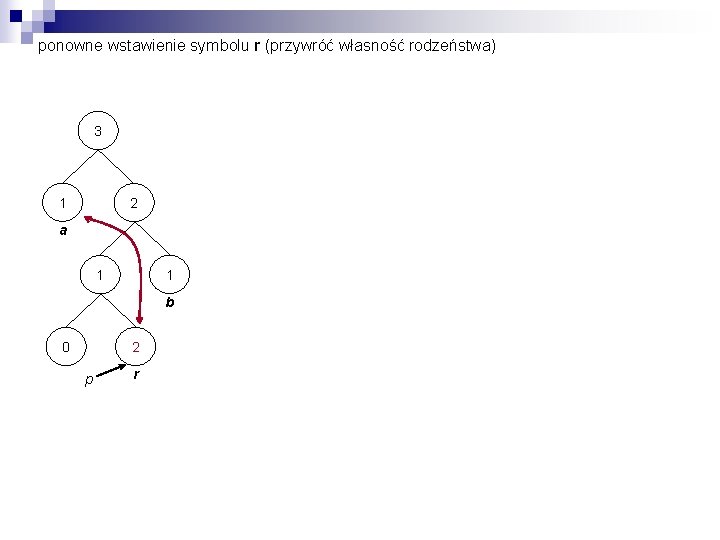
ponowne wstawienie symbolu r (ciąg abrr) r 3 1 2 a 1 1 b 0 1 r

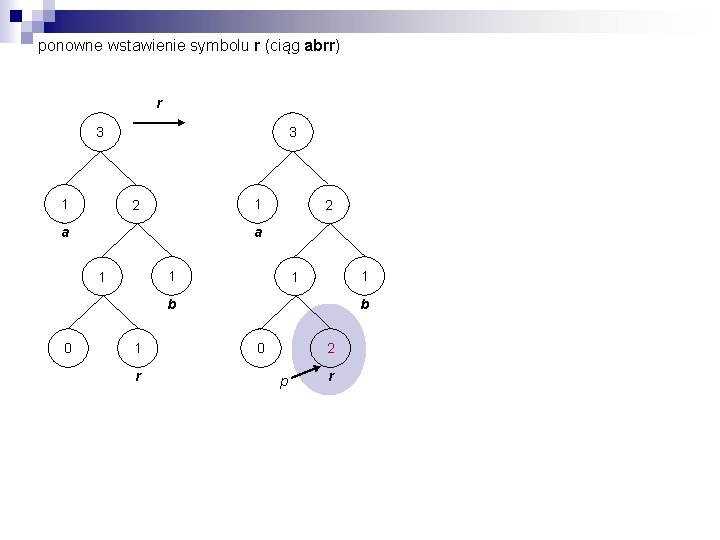
ponowne wstawienie symbolu r (ciąg abrr) r 3 1 2 a 1 1 b 0 1 r b 0 2 p r

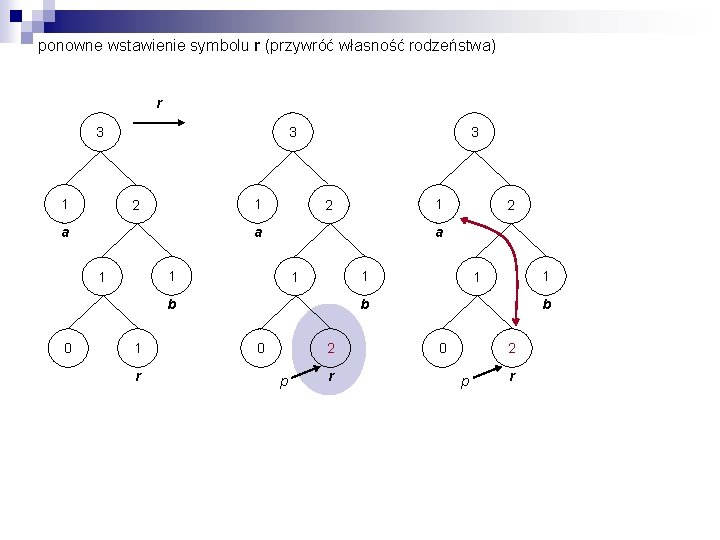
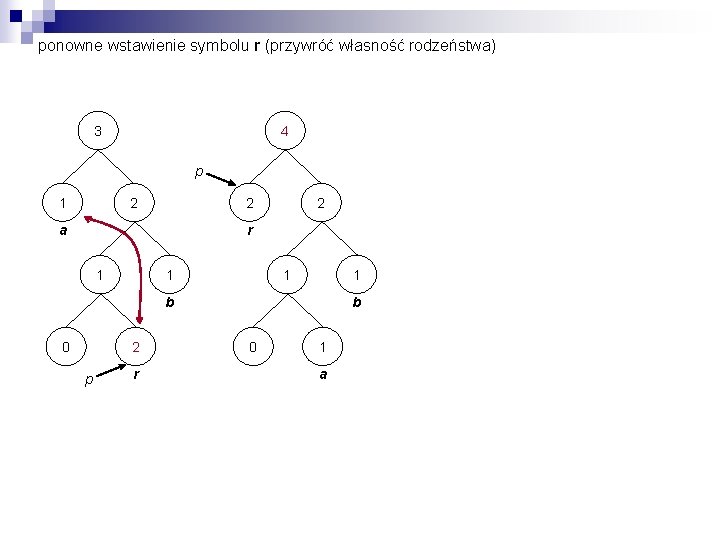
ponowne wstawienie symbolu r (przywróć własność rodzeństwa) r 3 1 2 a 3 a 1 1 b 1 r 2 a 1 1 0 1 2 1 1 b 0 2 p r

ponowne wstawienie symbolu r (przywróć własność rodzeństwa) 3 1 2 a 1 1 b 0 2 p r

ponowne wstawienie symbolu r (przywróć własność rodzeństwa) 3 4 p 1 2 2 a 2 r 1 1 b 0 2 p r b 0 1 a

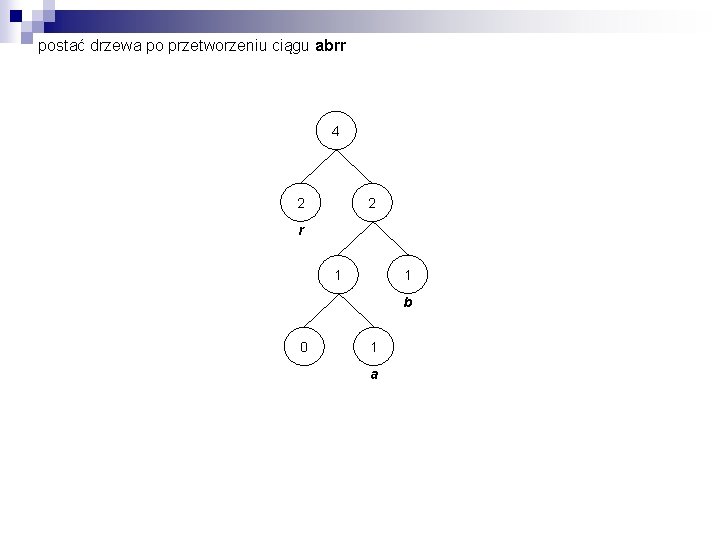
postać drzewa po przetworzeniu ciągu abrr 4 2 2 r 1 1 b 0 1 a

Algorytm Vittera Dodatkowe założenie: w bloku-i węzłów najpierw znajdują się węzły wewnętrzne, później liście n n minimalizujemy głębokość drzewa bardziej złożone staje się przywracanie własności rodzeństwa ciąg o długości s zakodujemy na nie więcej niż h+s bitach, gdzie h to liczba bitów dla kodowania statycznego Huffmana ¨ ten algorytm radzi sobie z ZFP lepiej, niż algorytm Fallera-Gallagera ¨ (dla niektórych ciągów wynik dynamicznego kodowania Huffmana może by lepszy, niż w statycznym algorytmie, bo tu nie przesyłamy modelu)

Adaptacyjny algorytm kompresji z wykorzystaniem rodziny kodów (Golomb, Golomb-Rice) n Algorytm adaptacyjny można zbudować z kilku stałych modeli n Ale po kolei. . . Zmodyfikowane kody binarne ¨ Rodzina kodów Golomba-Rice’a ¨ Model danych dla parametrycznej rodziny kodów (model algorytmu FELICS) ¨

Zmodyfikowany kod binarny n prefiksowy kod dla skończonego alfabetu, np. dla liczb 0. . j-1 słowa kodowe o długości log(j) lub log (j) bitów, gdzie j to rozmiar alfabetu ¨ właściwie to rodzina kodów Alfabet ¨ Symbol ¨ (długość słowa kodowego kodu binarnego dla alfabetu j symboli to log(j) ) 0. . 4 0. . 5 0. . 6 0. . 7 0 . 0 0 0 1 0 . 0 0 1 2 . 1 0 0 . 0 1 1 . 0 1 0 3 . 1 1 0 1 . 1 0 0 . 0 1 1 4 . 1 1 1 0 1 . 1 0 0 . 1 1 1 0 1 . 1 1 0 5 6 7 . 1 1 1

Zmodyfikowany kod binarny n Generowanie słowa kodowego ¨ ¨ kodujemy liczbę i zmodyfikowanym kodem binarnym dla liczb 0. . j – 1, przyjmijmy N = log(j) i n = 2 N jeżeli i < n – j zakoduj i za pomocą N – 1 -bitowego kodu binarnego else zakoduj i + n – j za pomocą N -bitowego kodu binarnego n Własności zmodyfikowanego kodu binarnego ¨ ¨ ¨ długość słowa kodowego: log(j) lub log (j) dla j = 2 N kod staje się N -bitowym kodem binarnym liczba dłuższych słów kodowych jest zawsze parzysta

Kod Golomba n Kody Golomba ¨ parametryczna rodzina kodów n n n przeznaczona do kodowania nieujemnych liczb całkowitych nieskończona parametrem kodu jest całkowite m, m > 0 ¨ zawiera kody optymalne dla wykładniczego rozkładu prawdopodobieństwa symboli (dla niektórych parametrów rozkładu) (nadaje się do źródeł o rozkładzie nierosnącym) ¨ słowa kodowe łatwe w generacji i dekodowaniu

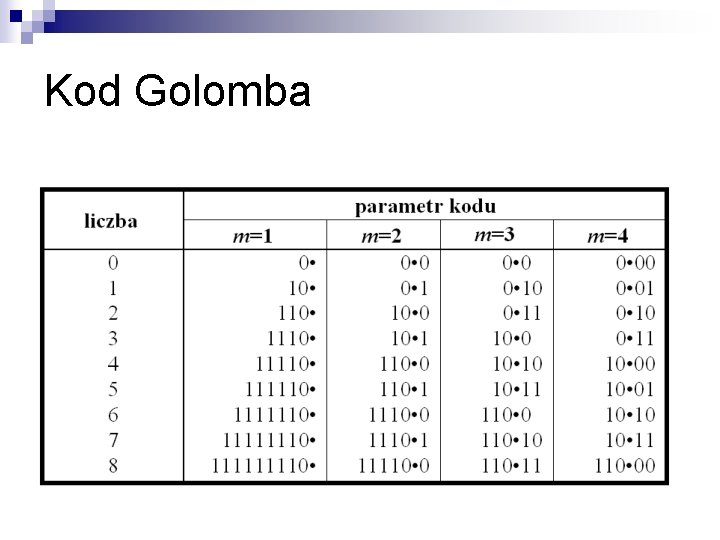
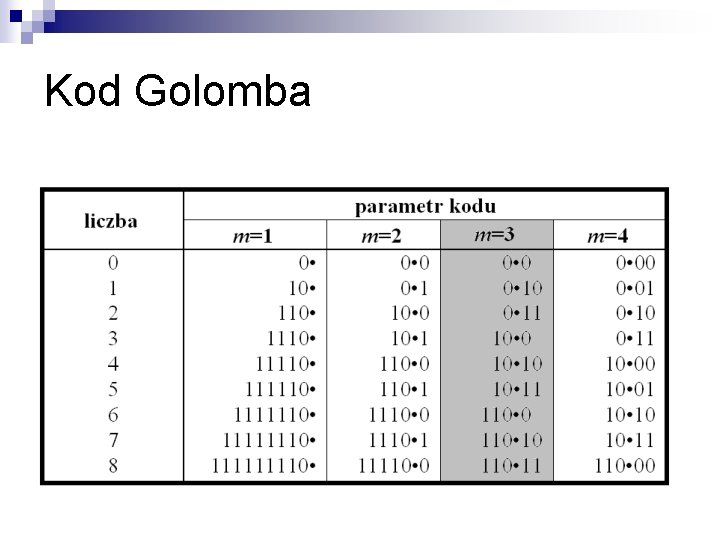
Kod Golomba

Kod Golomba n Generowanie słowa kodowego ¨ kodujemy liczbę x kodem Golomba z parametrem m prefiks słowa: x/m zakodowane unarnie (kod α Eliasa) sufiks: x mod m zakodowane zmodyfikowanym kodem binarnym dla przedziału [0, m – 1]

Kod Golomba n Generowanie słowa kodowego ¨ kodujemy liczbę x kodem Golomba z parametrem m np. 8 kodem Golomba z parametrem 3 prefiks słowa: x/m 8/3 = 2 zakodowane unarnie (kod α Eliasa) 110 sufiks: x mod m zakodowane zmodyfikowanym kodem binarnym dla przedziału [0, m – 1] 8 mod 3 = 2 11

Kod Golomba

Kod Golomba-Rice’a n Jest to szczególny przypadek kodu Golomba zauważony już przez Golomba i niezależnie od niego odkryty przez Rice’a: ¨ Kody Golomba są szczególnie proste, gdy m = 2 k ¨ kodujemy liczbę x kodem Golomba-Rice’a z parametrem k prefiks słowa: x/ 2 k x >> k zakodowane unarnie (kod α Eliasa) sufiks: x mod 2 k zakodowane zmodyfikowanym kodem binarnym dla przedziału [0, m – 1] k najmniej znaczących bitów x

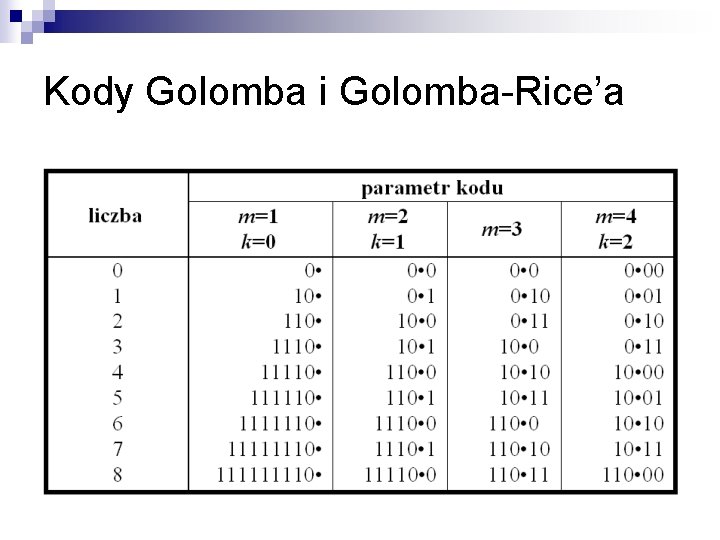
Kody Golomba i Golomba-Rice’a n Dla skończonego alfabetu używamy tylko części nieskończonej rodziny przyjmijmy rozmiar alfabetu 2 N ¨ dla rodziny Golomba kody o m > 2 N-1 mają słowa kodowe wszystkich symboli alfabetu dłuższe od kodu o m = 2 N-1 n ¨ sensowne jest używanie początkowych 2 N-1 kodów dla kodów Golomba-Rice’a kody o k > N – 1 mają słowa wszystkich symboli alfabetu dłuższe od kodu o k = N – 1 n sensowne jest używanie początkowych N kodów (k = 0. . N – 1 )

Kody Golomba i Golomba-Rice’a

Model danych dla parametrycznej rodziny kodów n Rodziny Golomba-Rice’a można użyć do kodowania ciągów symboli o wykładniczym rozkładzie prawdopodobieństwa. (rozkład często spotykany w kompresji obrazów, dźwięków. . . ) n Jeżeli parametr rozkładu jest nieznany, lub zmienia się w trakcie pracy źródła to parametr kodu Golomba-Rice’a trzeba dobierać adaptacyjnie n Jak to zrobić ?

Model danych dla parametrycznej rodziny kodów n Jak to zrobić ? n to proste. . . n Wybierajmy ten kod, który jest najlepszy dla już przetworzonych symboli n Jak to zrobić?

Model algorytmu FELICS dla parametrycznej rodziny kodów n Algorytm modelowania zastosowany przez Howarda i Vittera w algorytmie bezstratnej kompresji obrazów FELICS n dla każdego kodu z rodziny utrzymuj licznik (tablica liczników) ¨ licznik liczby bitów, którą uzyskano by kodując dotychczas przetworzoną część ciągu tym kodem ¨ po zakodowaniu symbolu zwiększ licznik każdego z kodów o długość słowa kodowego właśnie zakodowanego symbolu w kodzie odpowiadającym licznikowi ¨ do kodowania symbolu użyj kodu o najmniejszym liczniku

Model algorytmu FELICS dla parametrycznej rodziny kodów ¨ udoskonalenie: okresowo, gdy wartość najmniejszego z liczników przekroczy pewien próg, podziel wszystkie liczniki przez 2 n n unikniemy przepełnienia zwiększymy znaczenie symboli kodowanych niedawno ¨ ww. metoda to tylko część całego algorytmu (i tylko część modelu) ¨ metoda z FELICS nadaje się do każdej rodziny ¨ jeszcze prostsza metoda istnieje dla rodziny Golomba-Rice’a n n Zastosowana przez Weinberger, Seroussi, Sapiro w algorytmie LOCO(JPEG -LS) Niezależnie od rozmiaru alfabetu mamy 2 liczniki (licznik zakodowanych symboli i licznik sumy wartości tych symboli)