16 CLASSICAL CONFIGURATIONS Fano plane 73 We can

16. CLASSICAL CONFIGURATIONS

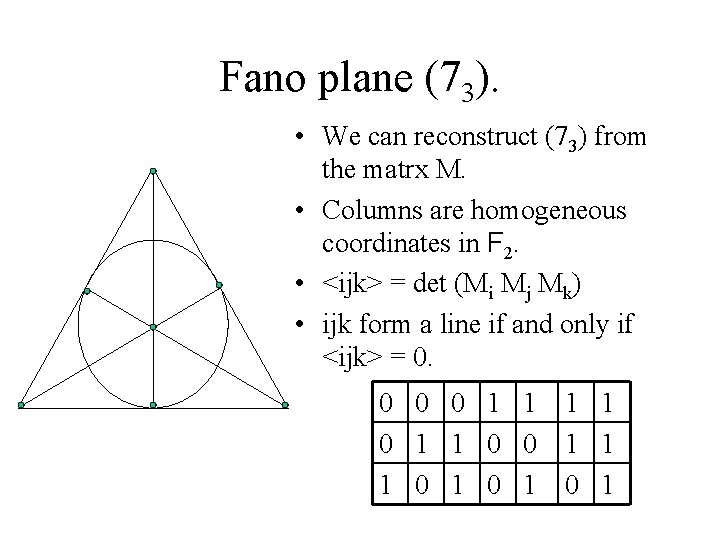
Fano plane (73). • We can reconstruct (73) from the matrx M. • Columns are homogeneous coordinates in F 2. • <ijk> = det (Mi Mj Mk) • ijk form a line if and only if <ijk> = 0. 0 0 0 1 1 0 0 1 0 1 1 1 0 1

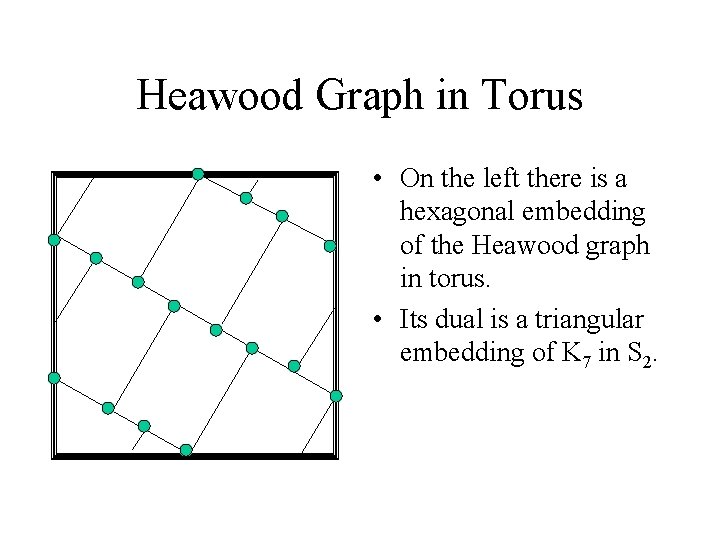
Heawood Graph in Torus • On the left there is a hexagonal embedding of the Heawood graph in torus. • Its dual is a triangular embedding of K 7 in S 2.

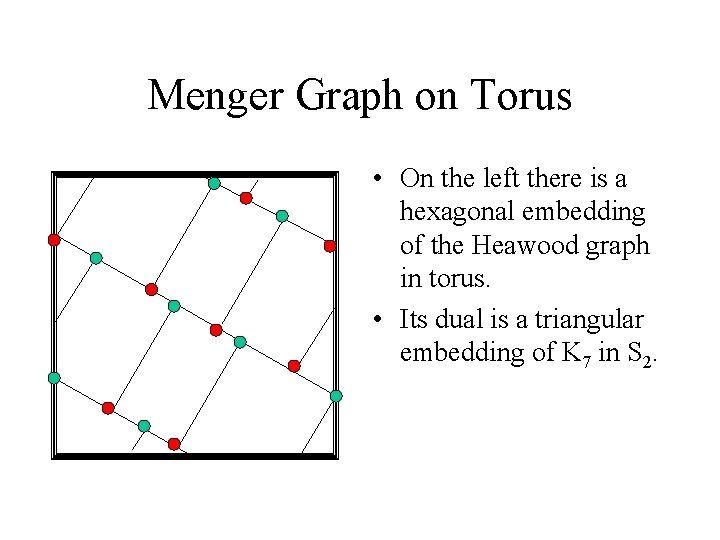
Menger Graph on Torus • On the left there is a hexagonal embedding of the Heawood graph in torus. • Its dual is a triangular embedding of K 7 in S 2.

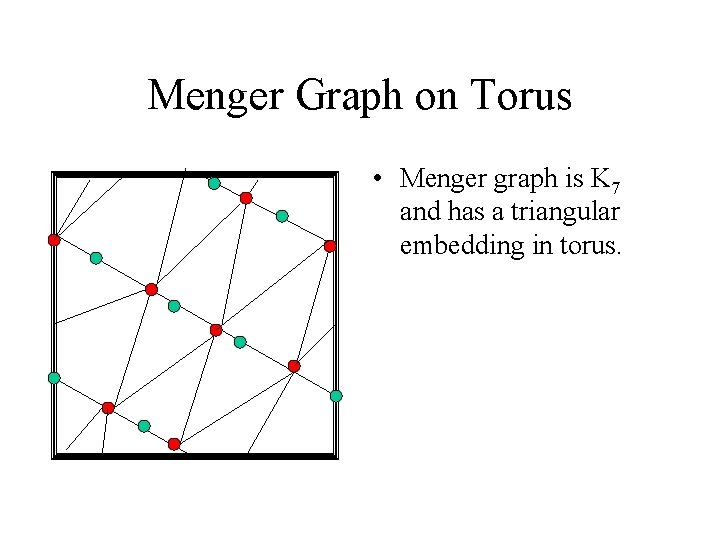
Menger Graph on Torus • Menger graph is K 7 and has a triangular embedding in torus.

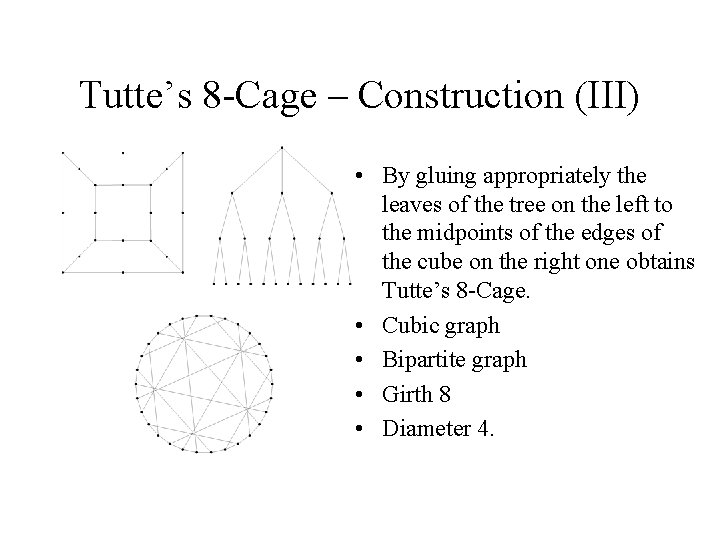
Tutte’s 8 -Cage – Construction (III) • By gluing appropriately the leaves of the tree on the left to the midpoints of the edges of the cube on the right one obtains Tutte’s 8 -Cage. • Cubic graph • Bipartite graph • Girth 8 • Diameter 4.

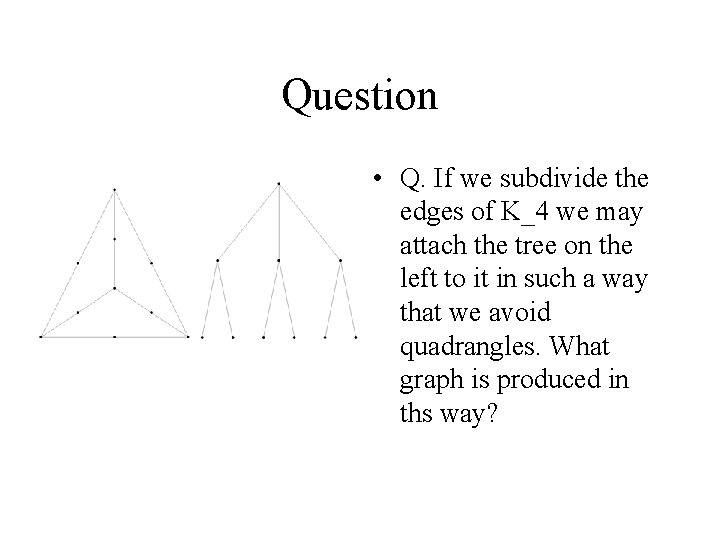
Question • Q. If we subdivide the edges of K_4 we may attach the tree on the left to it in such a way that we avoid quadrangles. What graph is produced in ths way?

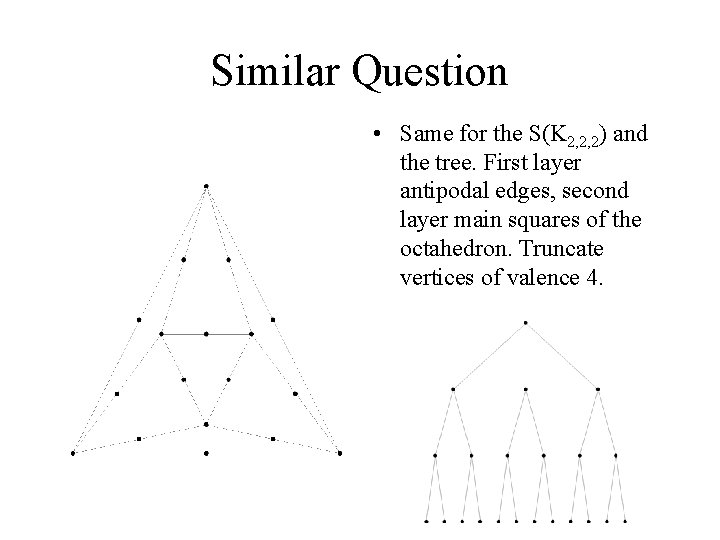
Similar Question • Same for the S(K 2, 2, 2) and the tree. First layer antipodal edges, second layer main squares of the octahedron. Truncate vertices of valence 4.

Möbius-Kantor Configuration – Revisited • Möbius-Kantor configuration is the only (83) configuration. Its Levi graph is the generalized Petersen graph G(8, 3). • The configuration has no geometric realization.

Complex Coordinatization of (94, 123)

A Z 3 coordinatization of (134) = PG(2, 3)

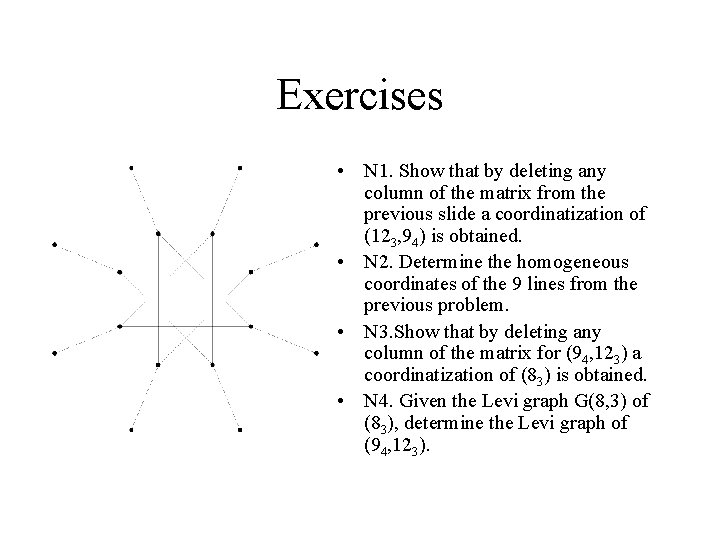
Exercises • N 1. Show that by deleting any column of the matrix from the previous slide a coordinatization of (123, 94) is obtained. • N 2. Determine the homogeneous coordinates of the 9 lines from the previous problem. • N 3. Show that by deleting any column of the matrix for (94, 123) a coordinatization of (83) is obtained. • N 4. Given the Levi graph G(8, 3) of (83), determine the Levi graph of (94, 123).

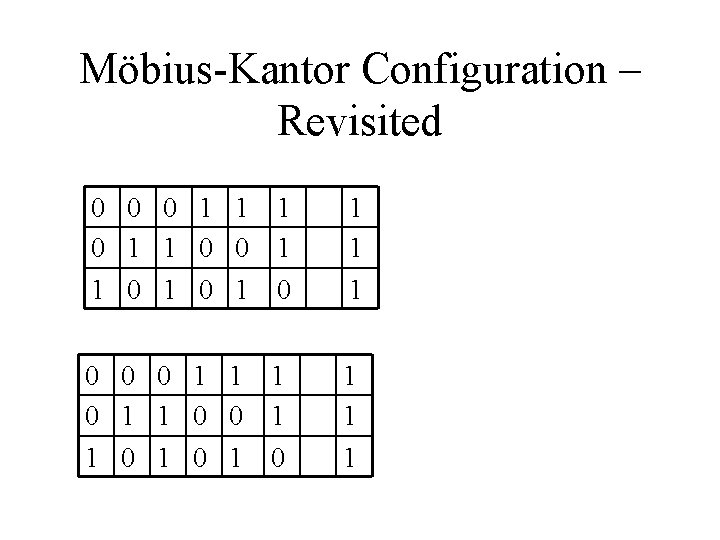
Möbius-Kantor Configuration – Revisited 0 0 0 1 1 1 0 0 1 1 0 1 0 1 0 1 1 1

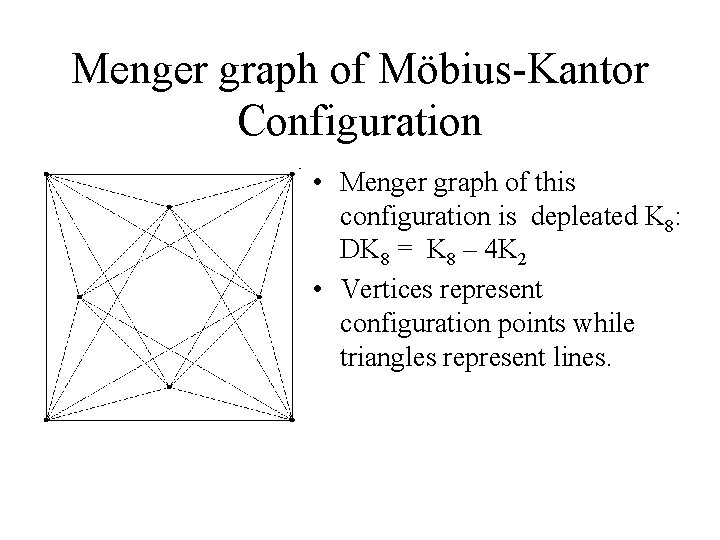
Menger graph of Möbius-Kantor Configuration • Menger graph of this configuration is depleated K 8: DK 8 = K 8 – 4 K 2 • Vertices represent configuration points while triangles represent lines.

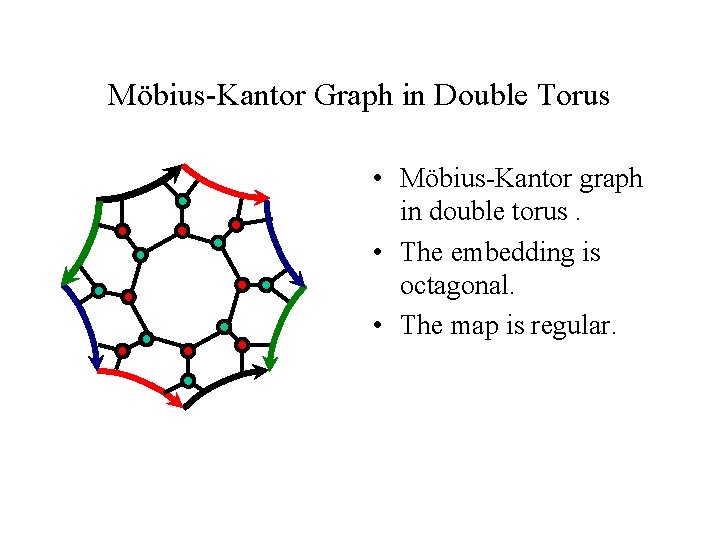
Möbius-Kantor Graph in Double Torus • Möbius-Kantor graph in double torus. • The embedding is octagonal. • The map is regular.

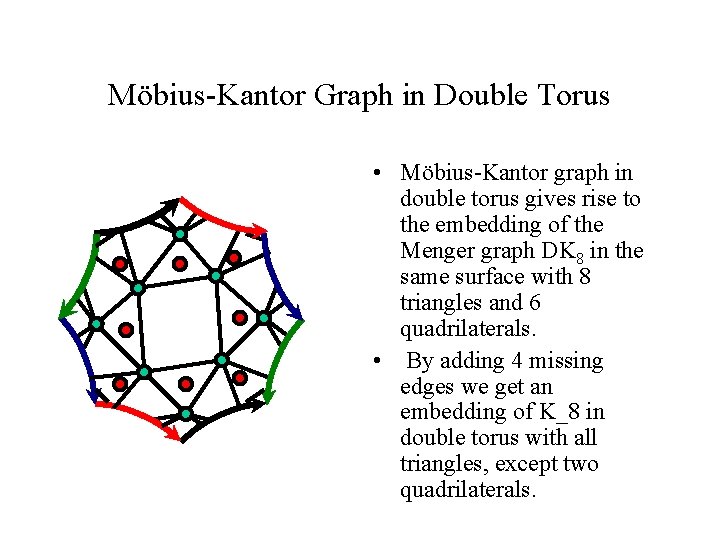
Möbius-Kantor Graph in Double Torus • Möbius-Kantor graph in double torus gives rise to the embedding of the Menger graph DK 8 in the same surface with 8 triangles and 6 quadrilaterals. • By adding 4 missing edges we get an embedding of K_8 in double torus with all triangles, except two quadrilaterals.

The Dual • The dual graph is S[2](K 4). • Let G be any graph. Recall that S(G) is the subdivision graph. • S[k](G) is obtained from S(G) by multiplying the original vertices of G k times.

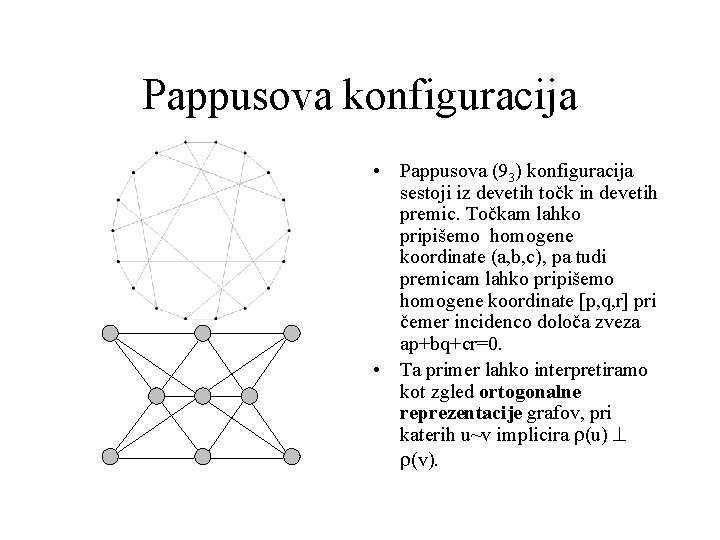
Pappusova konfiguracija • Pappusova (93) konfiguracija sestoji iz devetih točk in devetih premic. Točkam lahko pripišemo homogene koordinate (a, b, c), pa tudi premicam lahko pripišemo homogene koordinate [p, q, r] pri čemer incidenco določa zveza ap+bq+cr=0. • Ta primer lahko interpretiramo kot zgled ortogonalne reprezentacije grafov, pri katerih u~v implicira r(u) ^ r(v).

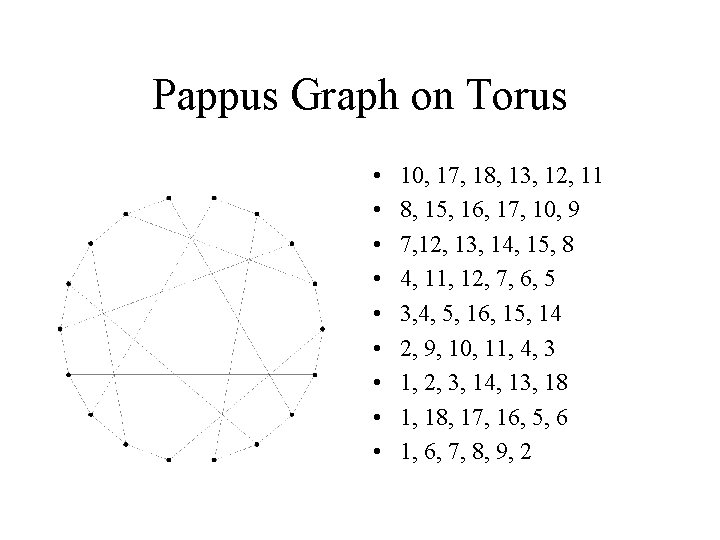
Pappus Graph on Torus • • • 10, 17, 18, 13, 12, 11 8, 15, 16, 17, 10, 9 7, 12, 13, 14, 15, 8 4, 11, 12, 7, 6, 5 3, 4, 5, 16, 15, 14 2, 9, 10, 11, 4, 3 1, 2, 3, 14, 13, 18 1, 18, 17, 16, 5, 6 1, 6, 7, 8, 9, 2

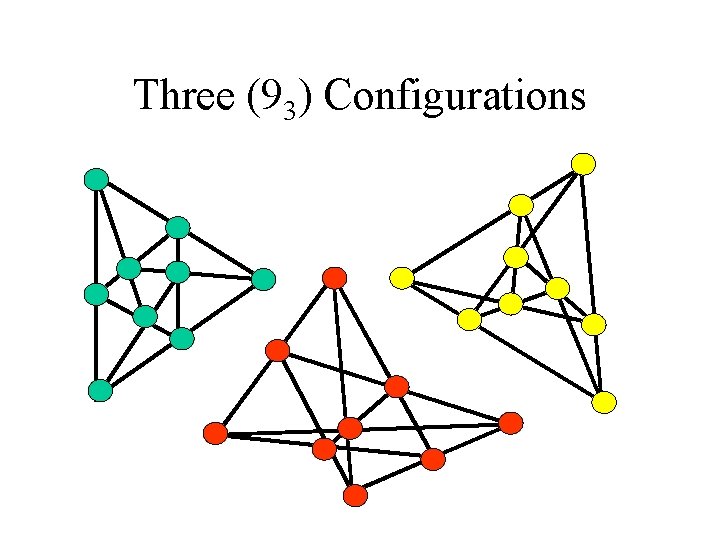
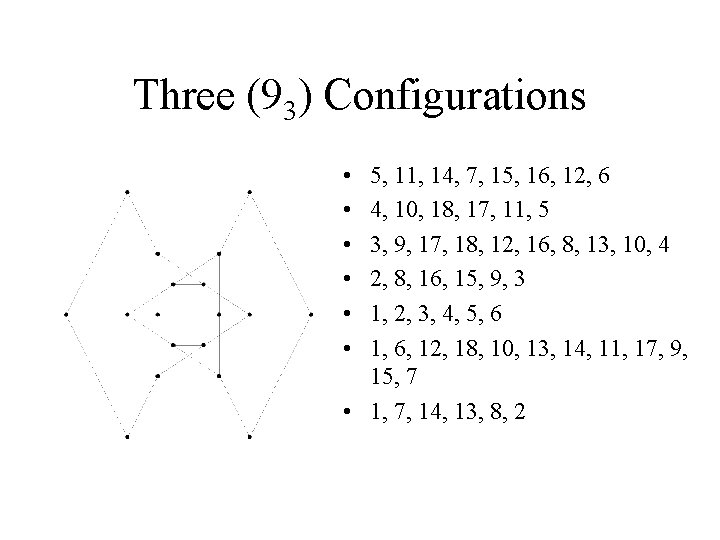
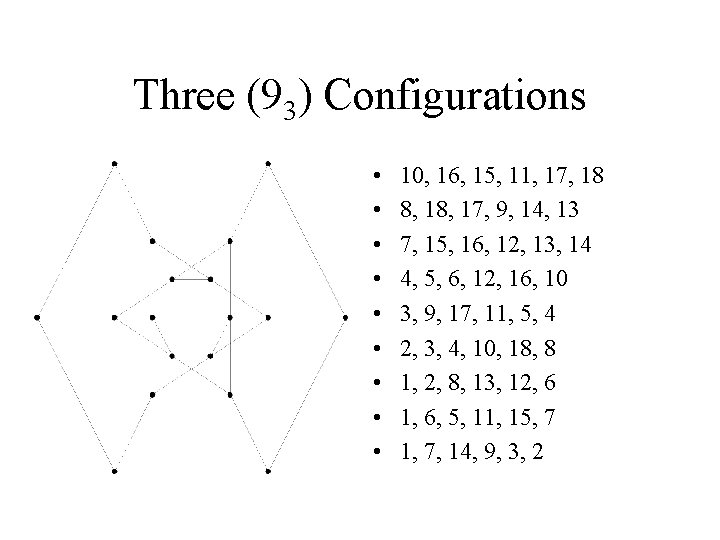
Three (93) Configurations

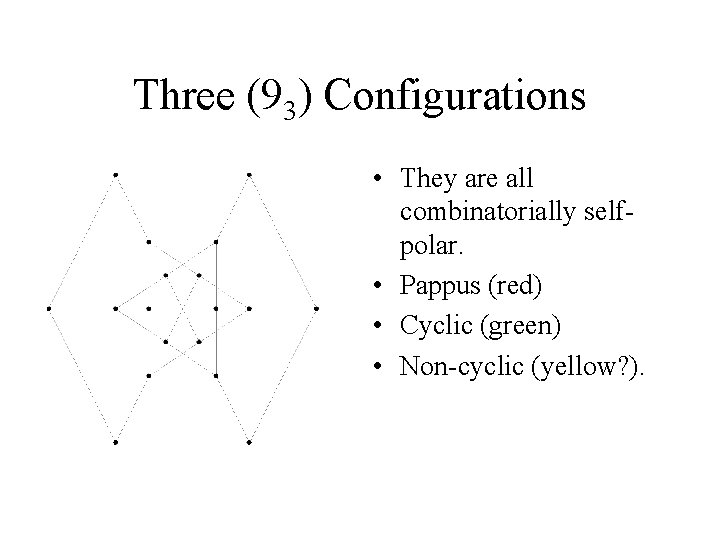
Three (93) Configurations • They are all combinatorially selfpolar. • Pappus (red) • Cyclic (green) • Non-cyclic (yellow? ).

Three (93) Configurations • • • 5, 11, 14, 7, 15, 16, 12, 6 4, 10, 18, 17, 11, 5 3, 9, 17, 18, 12, 16, 8, 13, 10, 4 2, 8, 16, 15, 9, 3 1, 2, 3, 4, 5, 6 1, 6, 12, 18, 10, 13, 14, 11, 17, 9, 15, 7 • 1, 7, 14, 13, 8, 2

Three (93) Configurations • • • 10, 16, 15, 11, 17, 18 8, 17, 9, 14, 13 7, 15, 16, 12, 13, 14 4, 5, 6, 12, 16, 10 3, 9, 17, 11, 5, 4 2, 3, 4, 10, 18, 8 1, 2, 8, 13, 12, 6 1, 6, 5, 11, 15, 7 1, 7, 14, 9, 3, 2

Exercises • N 1. Show that each (9_3) configuration is combinatorially self-polar. • N 2. Determine the groups of automorphisms and extended automorphisms. • N 3. Show that the genus of two configurations is 1 while the genus of the third one is 2. Make models! • N 4. Determine three Menger graphs and their duals on the minimal surfaces. • N 4. Prove that the complements of the three Menger graphs are respectively C 9, C 6 [ C 3, 3 C 3.

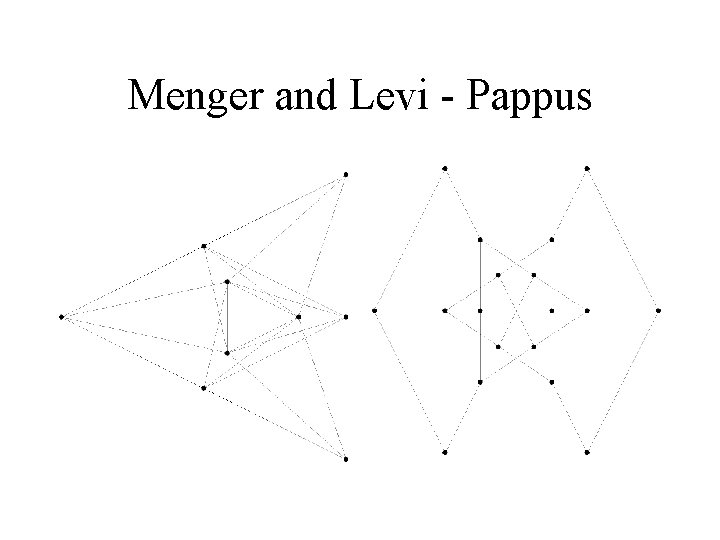
Menger and Levi - Pappus

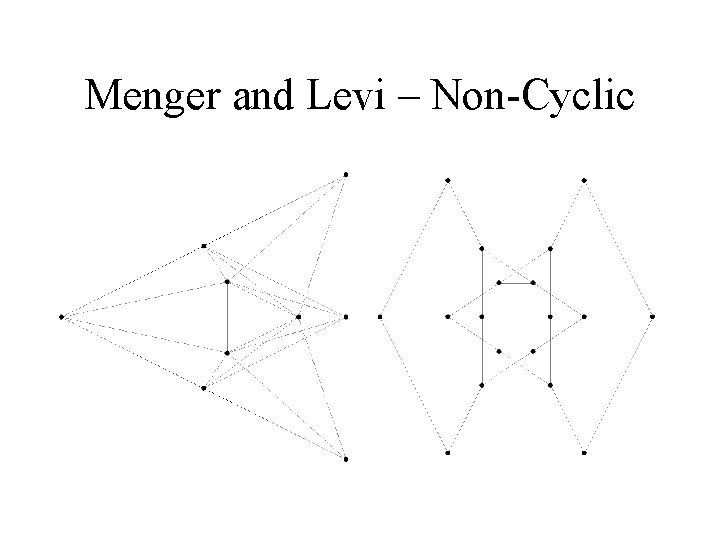
Menger and Levi – Non-Cyclic

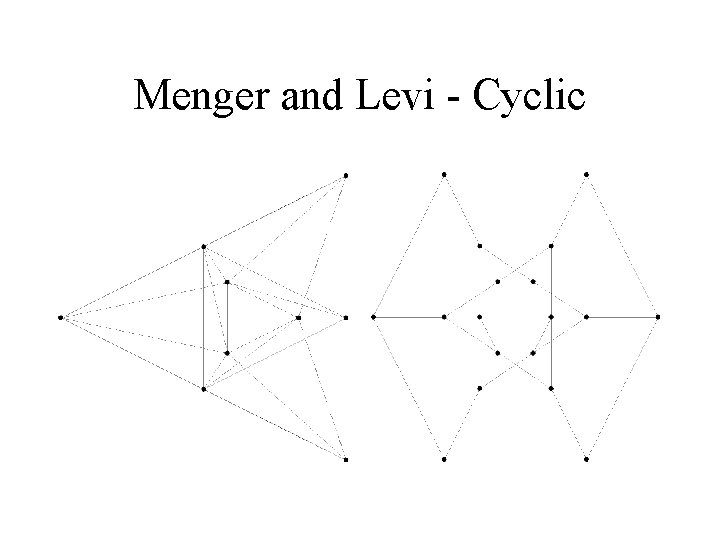
Menger and Levi - Cyclic

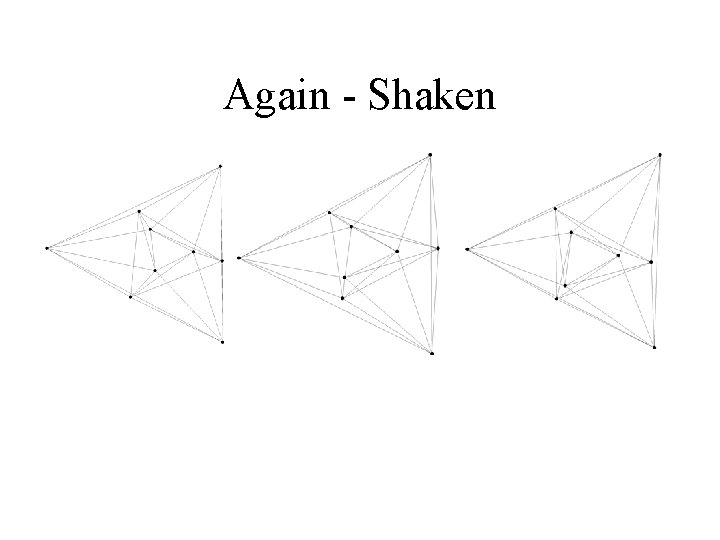
Again - Shaken

Menger and Its Complement of G(10, 3)

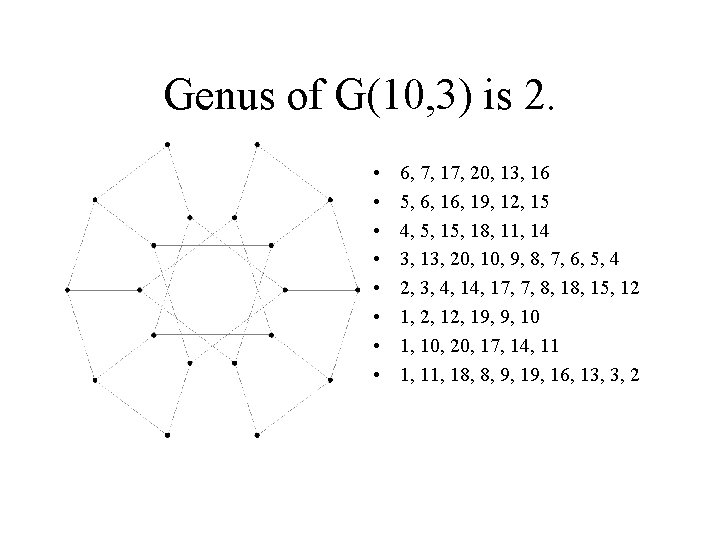
Genus of G(10, 3) is 2. • • 6, 7, 17, 20, 13, 16 5, 6, 19, 12, 15 4, 5, 18, 11, 14 3, 13, 20, 10, 9, 8, 7, 6, 5, 4 2, 3, 4, 17, 7, 8, 15, 12 1, 2, 19, 9, 10 1, 10, 20, 17, 14, 11 1, 18, 8, 9, 16, 13, 3, 2

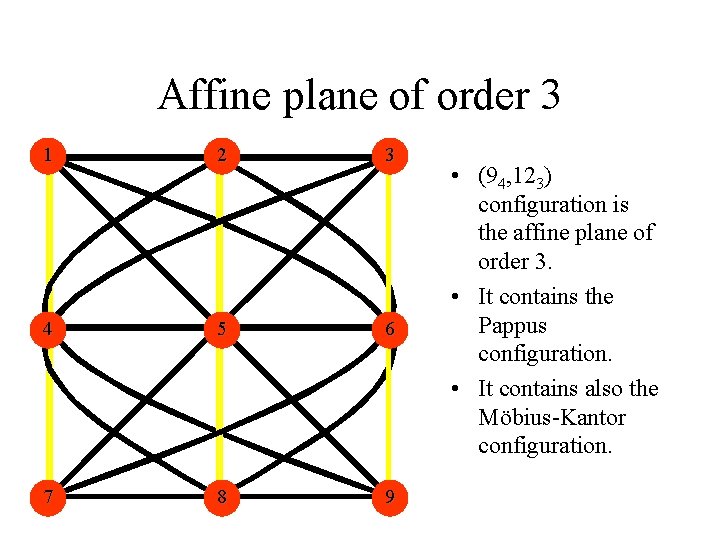
Affine plane of order 3 1 2 3 4 5 6 7 8 9 • (94, 123) configuration is the affine plane of order 3. • It contains the Pappus configuration. • It contains also the Möbius-Kantor configuration.

Clebschev šestkotnik

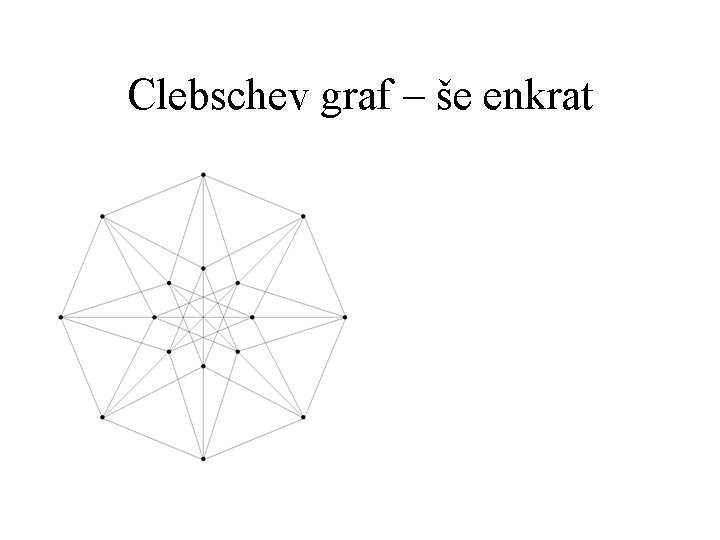
Clebschev šestkotnik – še enkrat

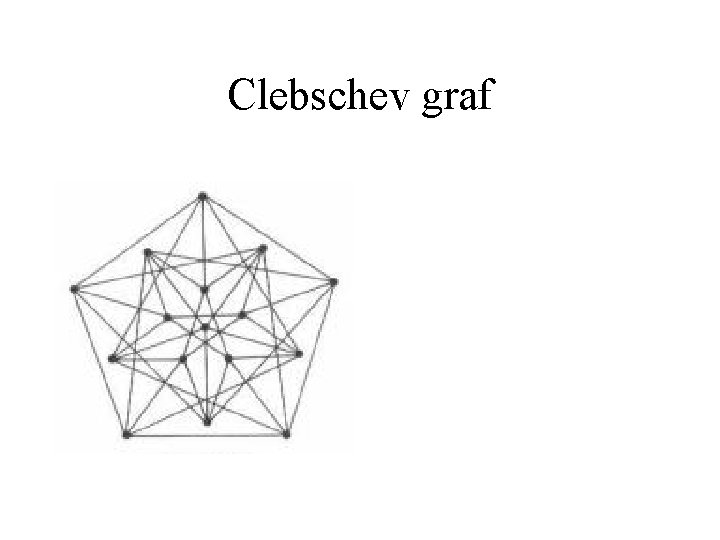
Clebschev graf

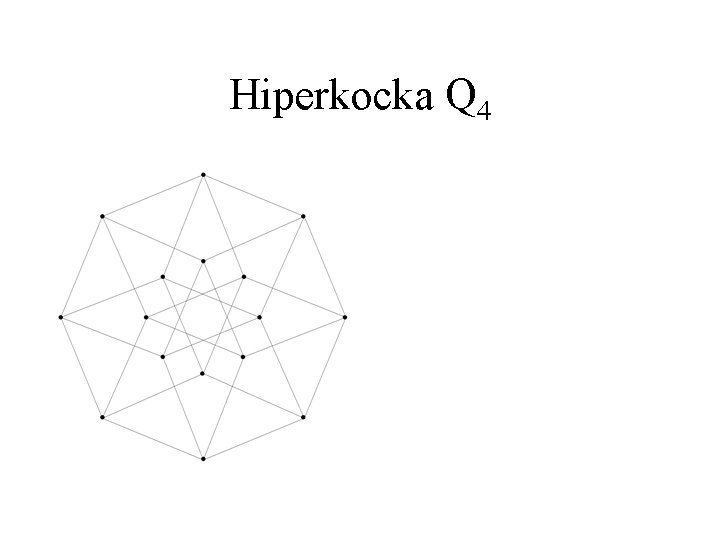
Hiperkocka Q 4

Clebschev graf – še enkrat

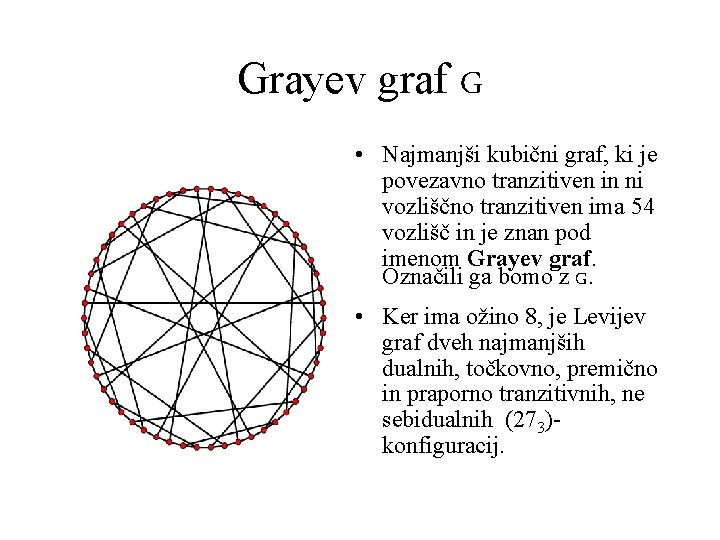
Grayev graf G • Najmanjši kubični graf, ki je povezavno tranzitiven in ni vozliščno tranzitiven ima 54 vozlišč in je znan pod imenom Grayev graf. Označili ga bomo z G. • Ker ima ožino 8, je Levijev graf dveh najmanjših dualnih, točkovno, premično in praporno tranzitivnih, ne sebidualnih (273)konfiguracij.

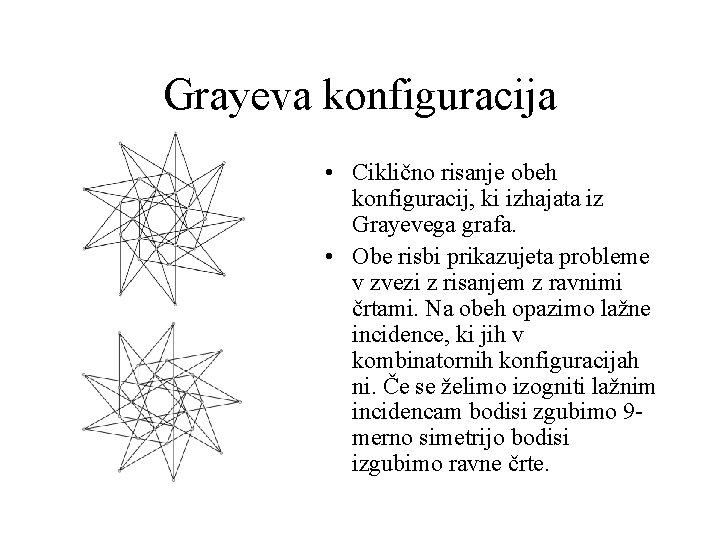
Grayeva konfiguracija • Ciklično risanje obeh konfiguracij, ki izhajata iz Grayevega grafa. • Obe risbi prikazujeta probleme v zvezi z risanjem z ravnimi črtami. Na obeh opazimo lažne incidence, ki jih v kombinatornih konfiguracijah ni. Če se želimo izogniti lažnim incidencam bodisi zgubimo 9 merno simetrijo bodisi izgubimo ravne črte.

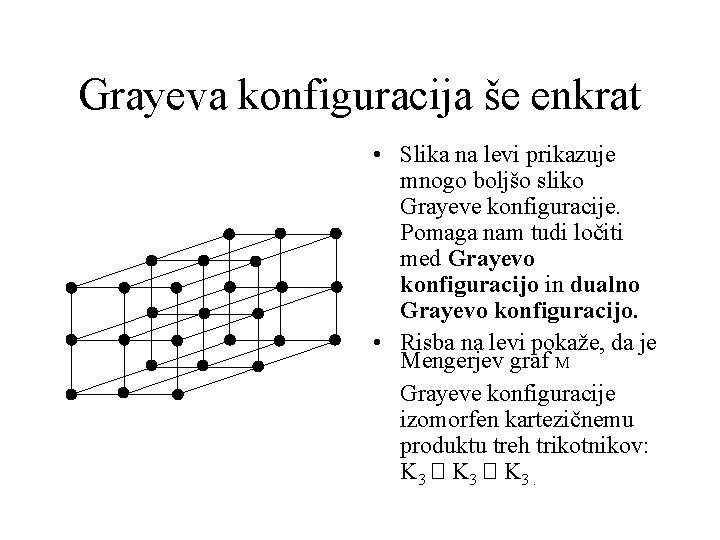
Grayeva konfiguracija še enkrat • Slika na levi prikazuje mnogo boljšo sliko Grayeve konfiguracije. Pomaga nam tudi ločiti med Grayevo konfiguracijo in dualno Grayevo konfiguracijo. • Risba na levi pokaže, da je Mengerjev graf M Grayeve konfiguracije izomorfen kartezičnemu produktu treh trikotnikov: K 3 � K 3.

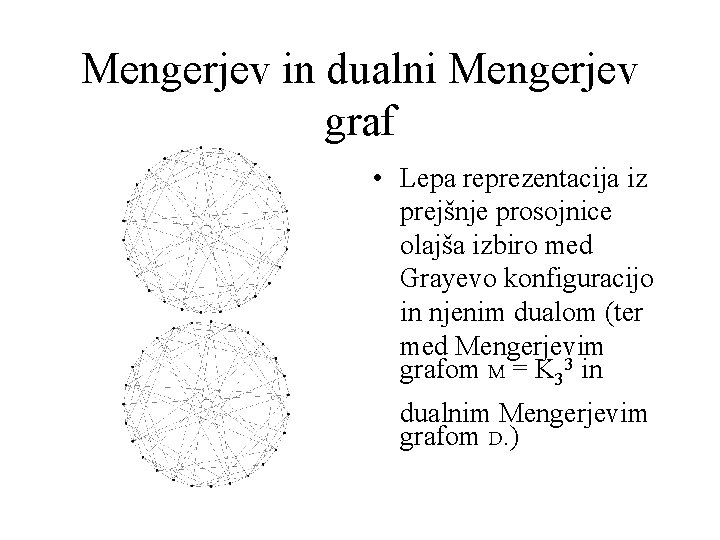
Mengerjev in dualni Mengerjev graf • Lepa reprezentacija iz prejšnje prosojnice olajša izbiro med Grayevo konfiguracijo in njenim dualom (ter med Mengerjevim grafom M = K 33 in dualnim Mengerjevim grafom D. )

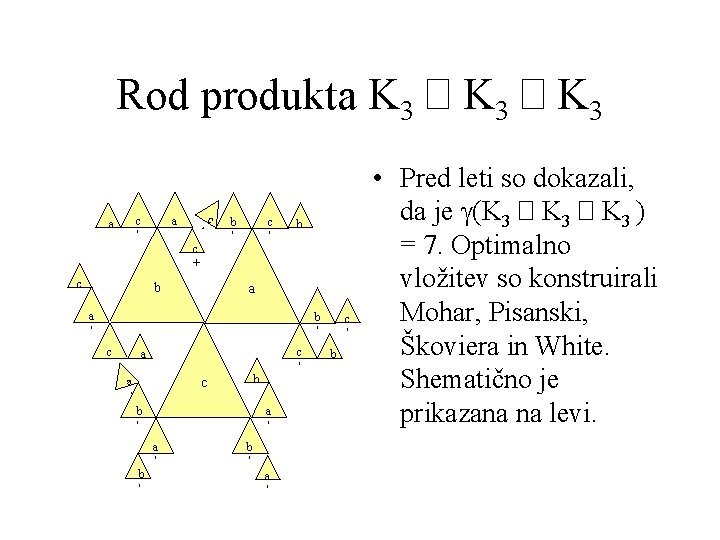
Rod produkta K 3 � K 3 c ' a a ' c c + c b b ' c ' b a a ' b ' c c ' a b c a ' b ' a ' c ' b • Pred leti so dokazali, da je g(K 3 � K 3 ) = 7. Optimalno vložitev so konstruirali Mohar, Pisanski, Škoviera in White. Shematično je prikazana na levi.

Optimalna vložitev • Optimalna vložitev s prejšnje prosojnice ima nekaj zelo lepih lastnosti: – Njen dual je dvodelni. – Vložitev uporabi vseh 27 trikotnikov grafa za lica – Če pobarvamo lica z dvema barvama, je vseh 27 trikotnikov pobarvanih z isto barvo. • Od tod pa sledi zelo pomembna ugotovitev: Točke Grayeve konfiguracije ustrezajo vozliščem, premice pa trikotnikom vložitve. Incidenca je seveda določena s povezavami.

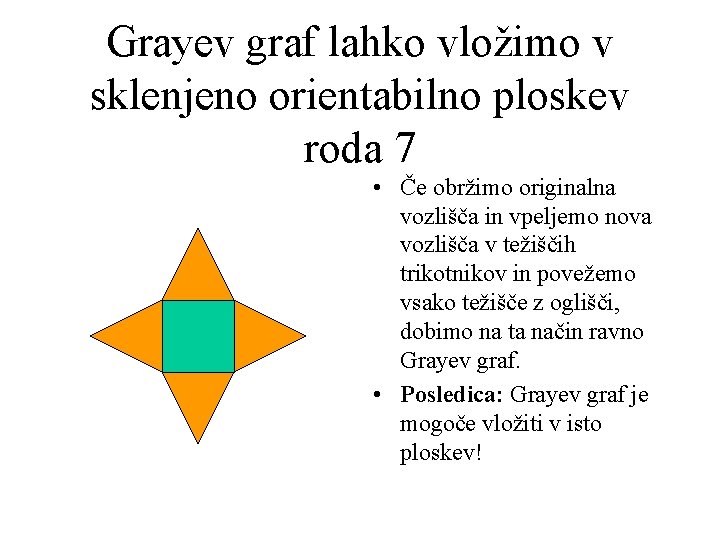
Grayev graf lahko vložimo v sklenjeno orientabilno ploskev roda 7 • Če obržimo originalna vozlišča in vpeljemo nova vozlišča v težiščih trikotnikov in povežemo vsako težišče z oglišči, dobimo na ta način ravno Grayev graf. • Posledica: Grayev graf je mogoče vložiti v isto ploskev!

Grayev graf lahko vložimo v sklenjeno orientabilno ploskev roda 7 • Če obržimo originalna vozlišča in vpeljemo nova vozlišča v težiščih trikotnikov in povežemo vsako težišče z oglišči, dobimo na ta način ravno Grayev graf. • Posledica: Grayev graf je mogoče vložiti v isto ploskev!

Spodnja meja • Zgornja meja je potemtakem 7. Da je tudi spodnja meja 7, sledi iz naslednjega rezultata: • Trditev: Naj bo L Levijev in M Mengerjev graf neke (v 3) konfiguracije C, tedaj velja ocena g(M) g(L). • Dokaz: Začnemo z optimalno vložitvijo grafa L. Že opisani proces lahko obrnemo (in vpeljemo trikotnike). Tako dobimo vložitev grafa M v isto ploskev.

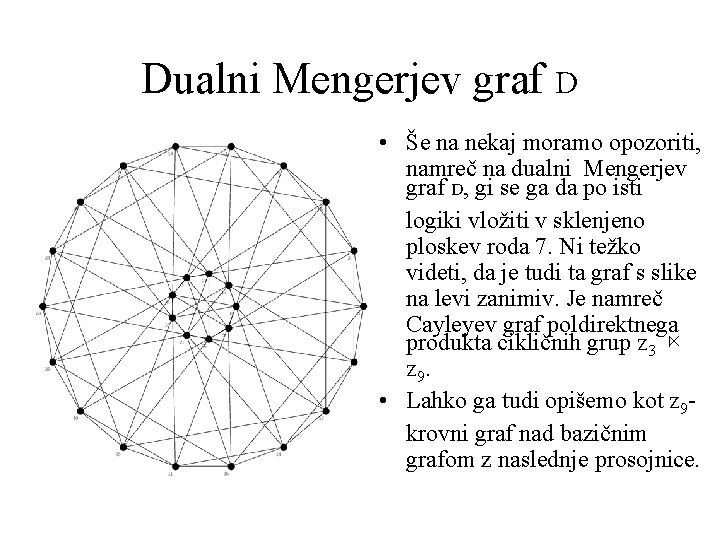
Dualni Mengerjev graf D • Še na nekaj moramo opozoriti, namreč na dualni Mengerjev graf D, gi se ga da po isti logiki vložiti v sklenjeno ploskev roda 7. Ni težko videti, da je tudi ta graf s slike na levi zanimiv. Je namreč Cayleyev graf poldirektnega produkta cikličnih grup Z 3 ⋉ Z 9. • Lahko ga tudi opišemo kot Z 9 krovni graf nad bazičnim grafom z naslednje prosojnice.

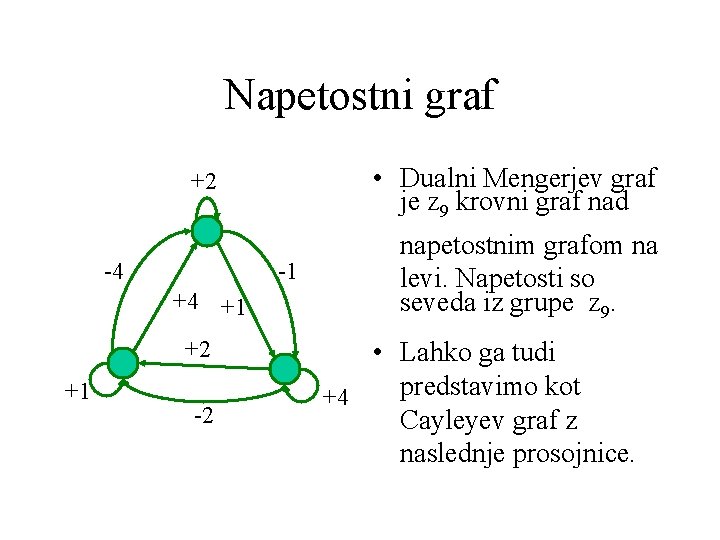
Napetostni graf • Dualni Mengerjev graf je Z 9 krovni graf nad +2 -4 -1 +4 +1 +2 +1 -2 napetostnim grafom na levi. Napetosti so seveda iz grupe Z 9. • Lahko ga tudi predstavimo kot +4 Cayleyev graf z naslednje prosojnice.

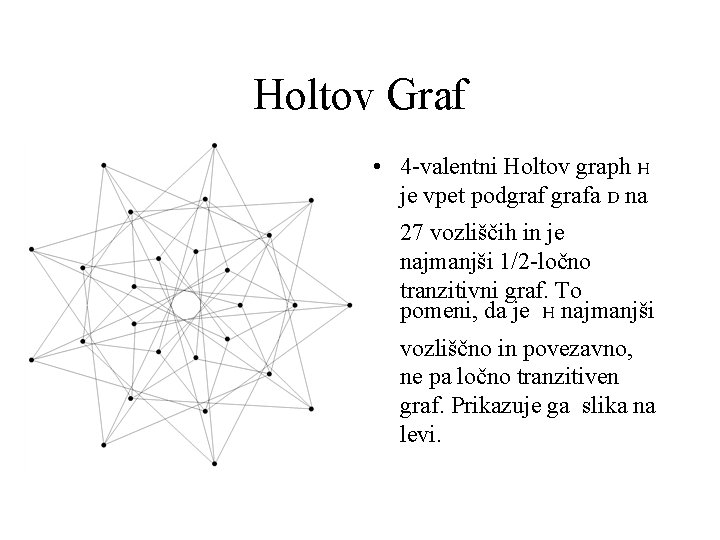
Holtov Graf • 4 -valentni Holtov graph H je vpet podgrafa D na 27 vozliščih in je najmanjši 1/2 -ločno tranzitivni graf. To pomeni, da je H najmanjši vozliščno in povezavno, ne pa ločno tranzitiven graf. Prikazuje ga slika na levi.

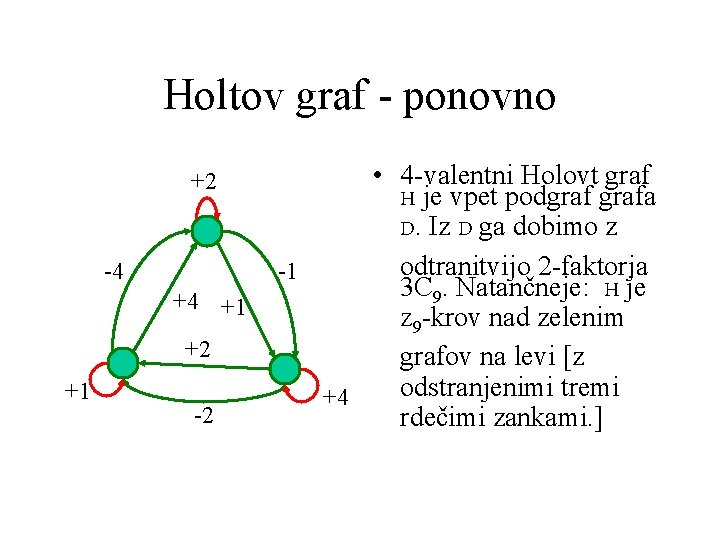
Holtov graf - ponovno +2 -4 +4 +1 +2 +1 -2 • 4 -valentni Holovt graf H je vpet podgrafa D. Iz D ga dobimo z odtranitvijo 2 -faktorja -1 3 C 9. Natančneje: H je Z 9 -krov nad zelenim grafov na levi [z odstranjenimi tremi +4 rdečimi zankami. ]

Nekaj prezentacij grupe Z 3 ⋉ Z 9 • Grafa H in D sta Cayleyeva grafa grupe Z 3 ⋉ Z 9. – Z 3 ⋉ Z 9 = <a, b | a 9 = b 3 = 1, b-1 ab = a 2> – D = <x, y, z | x 9 = y 9 = z 9 = 1, y-1 xy = x 2, y-1 zy = z 2, x-1 yx = y 2, x-1 zx = z 2, z-1 xz = x 2, z -1 yz = y 2> – H dobimo iz D če iz prezentacije odstranimo kateregakoli od x, y, z.

Nerešeni problemi • Kolikšen je rod grafa D? Kolikšen je rod grafa H? Rod grupe Z 3 ⋉ Z 9 je poznan: g(Z 3 ⋉ Z 9) = 4. Po drugi strani smo dokazali, da dopušča D vložitev v sklenjeno ploskev roda 7. Zato velja: – 4 g(D) 7 – 4 g(H) 7 • V prvem primeru bo najbrž lažje izboljšati spodnjo, v drugem pa zgornjo mejo.

Balabanova 10 -kletka • Na levi vidimo Balabanovo 10 kletko. To je najmanjši kubični graf ožine 10. Ima 70 vozlišč, vidimo tudi očitno simetrijo. • Kletka poseduje tudi Hamiltonov cikel. To vidimo npr. iz LCF kode zanjo: • [-9, -25, -19, 29, 13, 35, -13, -29, 19, 25, 9, -29, 17, 33, 21, 9, 13, -31, -9, 25, 17, 9, -31, 27, -9, 17, -19, -29, 27, -17, -9, -29, 33, -25, -21, 17, -17, 29, 35, -29, 17, -17, 21, -25, -33, 29, 9, 17, -27, 29, 19, -17, 9, -27, 31, 9, -17, -25, 9, 31, 13, -9, -21, 33, -17, -29, 29]

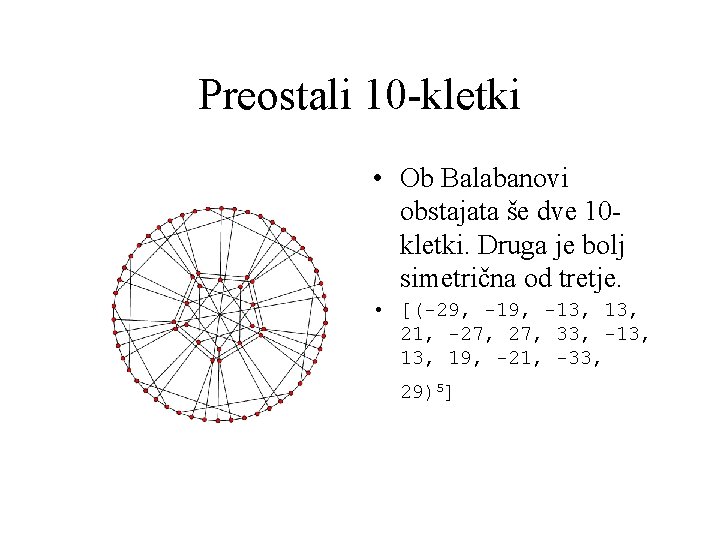
Preostali 10 -kletki • Ob Balabanovi obstajata še dve 10 kletki. Druga je bolj simetrična od tretje. • [(-29, -13, 13, 21, -27, 33, -13, 19, -21, -33, 29)5]

Preostali 10 -kletki • Ob Balabanovi obstajata še dve 10 -kletki. Tretja je najman simetrična. • [9, 25, 31, -17, 33, 9, -29, -15, -9, 9, 25, -25, 29, 17, -9, 9, -27, 35, -9, 9, -17, 21, 27, -29, -9, 25, 13, 19, -33, -17, 19, -31, 27, 11, -25, 29, 33, 13, -13, 21, -29, -21, 25, 9, -11, -19, 29, 9, 27, -19, -13, -35, -9, 9, 17, 25, -9, 9, 27, -27, 21, 15, -9, 29, -29, 33, 9, -25].

10 -kletke • Vse tri 10 -kletke so hamiltonske, zato smo jih lahko opisali z LCF kodo. • Grupe avtomorfizmov imajo rede: 80, 120, 24. • Literatura: T. P. , M. Boben, D. Marušič, A. Orbanič: The 10 -cages and derived Configurations, Discrete Math. 2003 (v tisku).