Wyrwnanie metod zawarunkowan z niewiadomymi Wstp Krakw 2019



















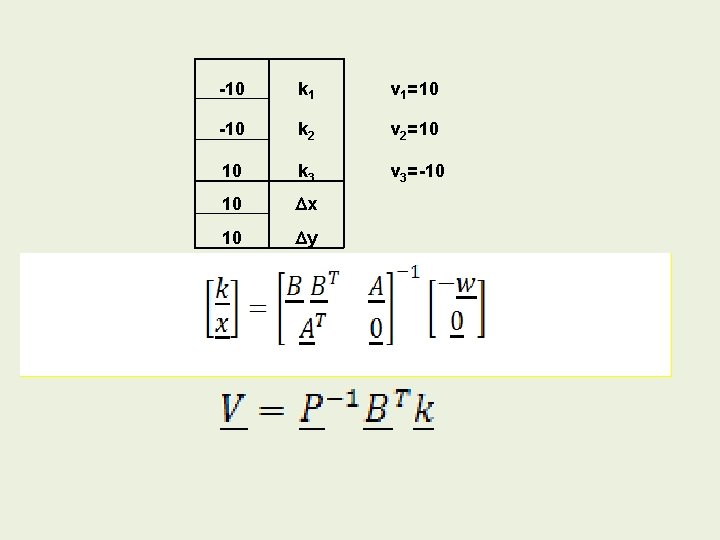


- Slides: 25

Wyrównanie metodą zawarunkowaną z niewiadomymi Wstęp Kraków 2019

Ausgleichungsrechnung II Gerhard Navratil Mit Beiträgen von Martin Staudinger Institute for Geoinformation Technical University Vienna Guβhausstraβe 27 -29 1040 Vienna, Austria

Metoda najmniejszych kwadratów została omówiona w ramach rachunku wyrównawczego. W niniejszym wykładzie przypomnimy najważniejsze zagadnienia z nią związane. W praktyce najczęściej mamy do czynienia z sytuacją w której wyznaczamy drogą pomiaru wielkości („Spostrzeżenia”) , za pomocą których obliczamy szukane parametry („Niewiadome”). Dysponujemy nadliczbowymi spostrzeżeniami w stosunku do liczby niezbędnych do wyznaczenia niewiadomych.

Umożliwia nam to : -kontrolę spostrzeżeń; -uzyskanie prawdopodobnych wartości niewiadomych; -ocenę dokładności wyników pomiarów oraz niezawodności sieci.

Wszystkie metody pomiarów (taśmą stalową czy GPS) prowadzą do stosunkowo prostego modelu matematycznego, związku między spostrzeżeniami i niewiadomymi, który może zostać opracowany za pomocą metody najmniejszych kwadratów. Ideę tej metody można zapisać wzorem: (1) gdzie: vi - poprawki spostrzeżeń; pi - wagi spostrzeżen; W zapisie macierzowym: (2)


Wartość prawdziwa nie jest możliwa do ustalenia, ale z pomocą metody najmniejszych kwadratów można uzyskać jej oszacowanie jako wektora spostrzeżeń wyrównanych :

Wektor parametrów X zawiera wartości niewiadomych X 1, X 2, . . . , Xu. Również wektor X jest wektorem losowym i ma wartość prawdziwą. Metodą najmniejszych kwadratów oblicza się jej oszacowanie, jako wektor wyrównany parametrów. Obliczamy go jako sumę wektora wartości przybliżonych X 0 oraz wektora poprawek niewiadomych x

Prawdziwe wartości spostrzeżeń i parametrów spełniają związek funkcyjny: Wyrównane, prawdopodobne wartości parametrów i spostrzeżeń spełniają podobne równanie zwane modelem funkcyjnym zadania wyrównawczego: Wartości obserwowane spostrzeżeń i przybliżone wartości parametrów nie będą zwykle spełniały tego równania.

Jeżeli do równania modelu funkcyjnego wstawimy wyniki spostrzeżeń i przybliżone wartości niewiadomych - zamiast wektora zerowego - po prawej stronie otrzymamy wektor odchyłek:

Funkcję należy doprowadzić do postaci liniowej, rozwijając ją w szereg Taylora z pominięciem wyrazów stopnia wyższego niż pierwszy:

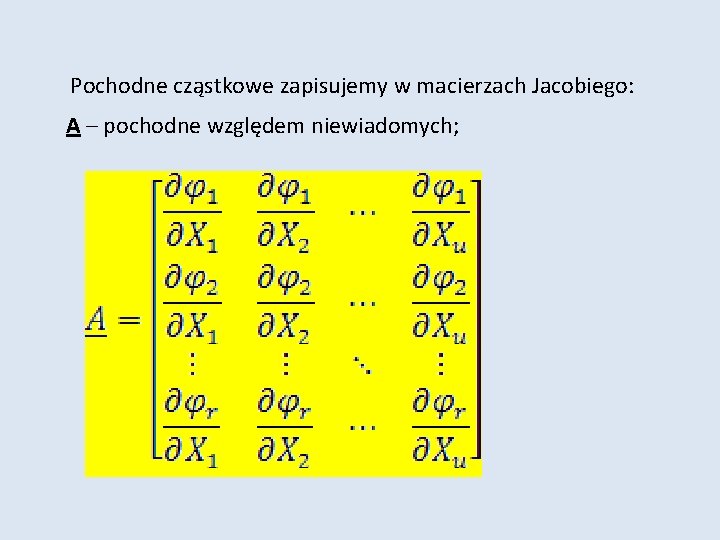
Pochodne cząstkowe zapisujemy w macierzach Jacobiego: A – pochodne względem niewiadomych;

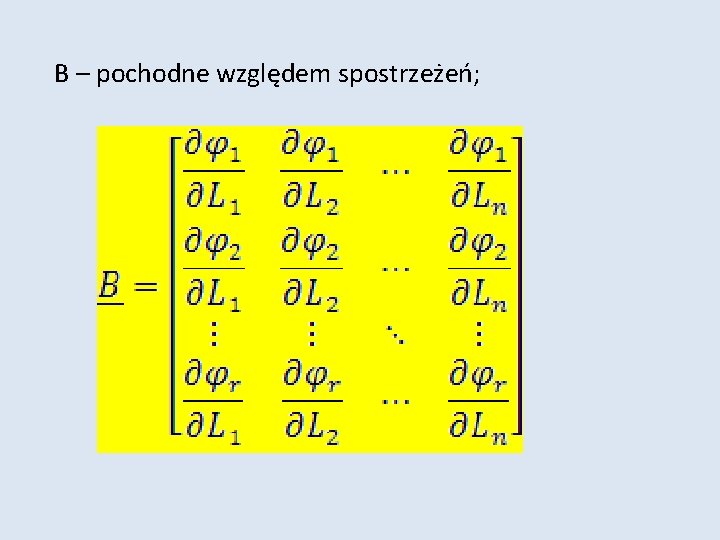
B – pochodne względem spostrzeżeń;

Możemy stosując powyższe oznaczenia zapisać ogólne zadanie rachunku wyrównawczego w następującej postaci:

Rozwiązanie ogólne: Jest to zadanie polegające z punktu widzenia matematyki na znalezieniu wartości ekstremalnej (minimum) z dodatkowymi warunkami. Takie zadanie rozwiązuje się stosując mnożniki Lagrange’a (zwane też przez geodetów korelatami). Wprowadzamy więc dodatkową macierz k.

Minimalizuje się funkcję Lagrange’a: Po obliczeniu pochodnych względem v oraz x i przyrównaniu ich do zera otrzymujemy wzory: oraz

W praktyce możemy mieć do czynienia z następującymi przypadkami: 1. W układzie równań r=n i w każdym równaniu występuje tylko jedno spostrzeżenie Li – jest to wyrównanie spostrzeżeń pośredniczących. 2. W zadaniu nie występują żadne niewiadome X. W r równaniach mamy tylko funkcje wiążące spostrzeżenia – jest to wyrównanie spostrzeżeń zawarunkowanych. 3. W n równaniach występuje po jednym spostrzeżeniu (jak przy wyrównaniu spostrzeżeń pośredniczących) a w pozostałych (r-n) równaniach mamy tylko niewiadome. Jest to wyrównanie spostrzeżeń pośredniczących z warunkami na niewiadome.


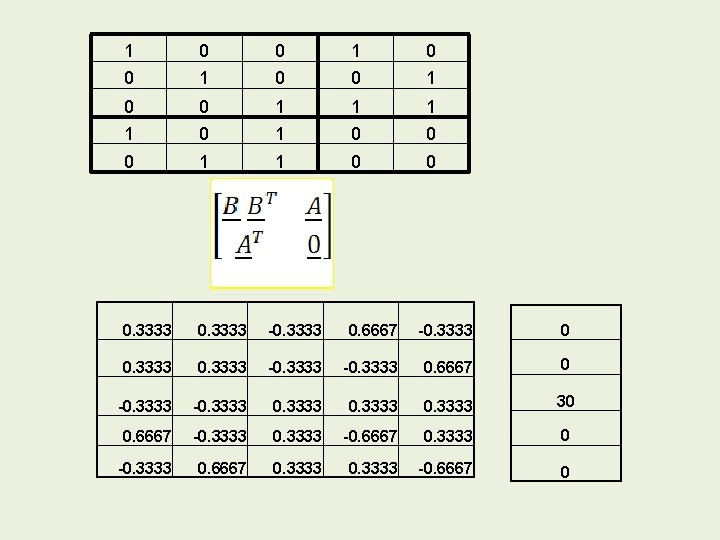
1 x 0 + x + 0 y 0 + 0 y - L 1 - v 1 = 0 0 x 0 + 0 x + 1 y 0 + y - L 2 - v 2 = 0 1 x 0 + 1 x + 1 y 0 + 1 y - L 3 - v 3 = 0 1 x + 0 y – v 1 + 1 = 0 0 x + 1 y – v 2 + 2 = 0 1 x + 1 y – v 3 + 3 = 0



1 0 0 1 1 0 1 0 0 0 1 1 0 0 0. 3333 -0. 3333 0. 6667 -0. 3333 0 0. 3333 -0. 3333 0. 6667 0 -0. 3333 30 0. 6667 -0. 3333 -0. 6667 0. 3333 0 -0. 3333 0. 6667 0. 3333 -0. 6667 0
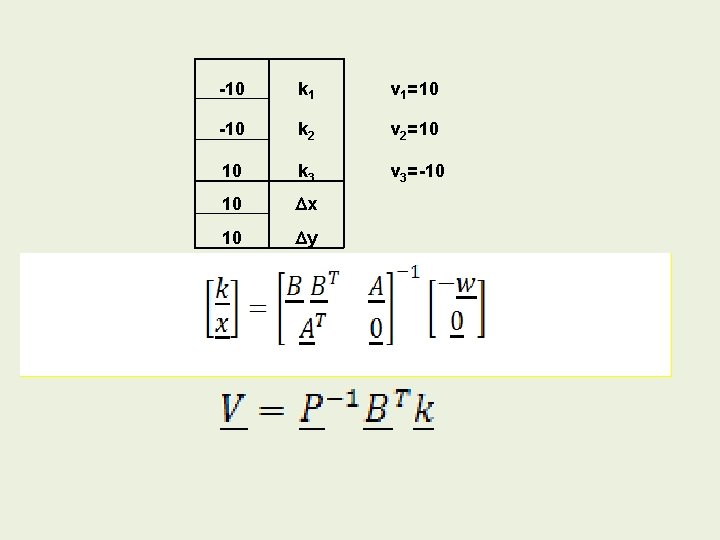
-10 k 1 v 1=10 -10 k 2 v 2=10 10 k 3 v 3=-10 10 Dx 10 Dy

Wyrównane spostrzeżenia i wyrównane niewiadome Kontrola generalna

Kontrola ogólna Ocena dokładności:
 Krakw
Krakw Gmk umk
Gmk umk Przykładowy raport kasowy
Przykładowy raport kasowy Felicia stabilizátor
Felicia stabilizátor Studiw
Studiw Wstp
Wstp Wstp
Wstp Matus kucera konstantin a metod
Matus kucera konstantin a metod Degresivni
Degresivni Metody aktywizujące podział
Metody aktywizujące podział Gap-analys metod
Gap-analys metod Pedagogik kengash shakllari
Pedagogik kengash shakllari Talim metodlari va usullari
Talim metodlari va usullari Cyril a metod 863
Cyril a metod 863 Ko'rgazmali metod
Ko'rgazmali metod Multisystemisk terapi
Multisystemisk terapi Hzda
Hzda Metod bild
Metod bild Operacije sa iskazima
Operacije sa iskazima Podział metod chromatograficznych
Podział metod chromatograficznych Interfaol metodlar slayd
Interfaol metodlar slayd Testimplikation
Testimplikation Uppsats exempel
Uppsats exempel Metody nauczania wg szloska
Metody nauczania wg szloska Delfi metoda
Delfi metoda Kabinet diagnostických metod fss
Kabinet diagnostických metod fss