Wykad 22 10 Ruch drgajcy 10 1 Oscylator




















- Slides: 25

Wykład 22 10 Ruch drgający 10. 1 Oscylator harmoniczny 10. 1. 1 Człony nieliniowe w równaniu oscylatora harmonicznego 10. 1. 2 Wahadło torsyjne 10. 1. 3 Ciekłe wahadło 10. 1. 4 Elektryczny układ drgający 10. 1. 5 Średnia energia swobodnego oscylatora harmonicznego 10. 1. 6 Wpływ tarcia na ruch 10. 2 Oscylator harmoniczny tłumiony 10. 3 Współczynnik dobroci oscylatora harmonicznego Reinhard Kulessa 15. 12. 2008 1

10 Ruch drgający 10. 1 Oscylator harmoniczny Drgania harmoniczne spotykamy w wielu dziedzinach fizyki klasycznej i kwantowej. Na tym wykładzie rozważaliśmy już przykłady ruchów harmonicznych. W oparciu o siłę sprężystości sprężyny może również drgać masa w kierunku poziomym. Innym przykładem ruchów harmonicznych są wszelkiego rodzaju wahadła. 15. 12. 2008 Reinhard Kulessa 2

Do postaci matematycznej równania opisującego ruch harmoniczny możemy dojść w różny sposób. Ogólnie właściwości oscylatora harmonicznego możemy scharakteryzować następująco: Jeśli układ oscyluje, to przechodzi on przez stan w którym w spoczynku jest w równowadze. 1. Częstość drgań oscylatora nie zależy od amplitudy wychyleń, 2. Jeżeli na drgający oscylator działa wiele sił, to zmiany nimi wywołane sumują się liniowo. Przypomnijmy sobie równanie oscylatora harmonicznego na przykładzie drgającej sprężyny stosując zasadę zachowania energii. . 15. 12. 2008 Reinhard Kulessa 3

Oznaczyliśmy . Różniczkując drugie równanie na poprzedniej stronie po czasie otrzymujemy; Pamiętając, że , oraz że , otrzymujemy, , skąd otrzymujemy, . 15. 12. 2008 Reinhard Kulessa (10. 1) 4

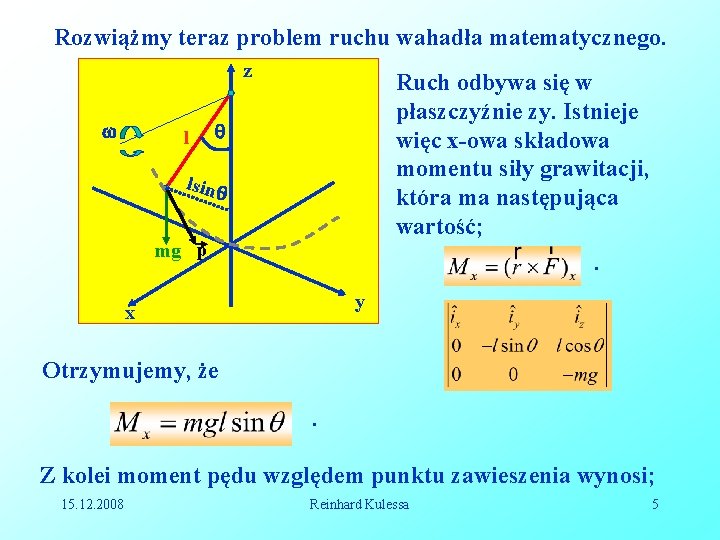
Rozwiążmy teraz problem ruchu wahadła matematycznego. z l Ruch odbywa się w płaszczyźnie zy. Istnieje więc x-owa składowa momentu siły grawitacji, która ma następująca wartość; lsin mg p . y x Otrzymujemy, że. Z kolei moment pędu względem punktu zawieszenia wynosi; 15. 12. 2008 Reinhard Kulessa 5

, gdzie wartość pędu jest równa; . Ponieważ szybkość zmian pędu jest równa momentowi siły działającej, możemy napisać; Dla bardzo małych kątów wychylenia sin . Możemy więc napisać; . (10. 2). Częstość drgań wahadła jest zgodnie z równaniem (10. 2) równa. 15. 12. 2008 Reinhard Kulessa 6

Ogólnym rozwiązaniem równania (10. 2) jest dowolna liniowa kombinacja funkcji sin 0 t, oraz cos 0 t. Możemy więc znaleźć rozwiązanie przy pomocy formuły Eulera; . Obierzmy ogólną postać rozwiązania równą; . (10. 3) Liczymy odpowiednie pochodne i wstawiamy do równania (10. 2). . 15. 12. 2008 Reinhard Kulessa 7

Ostatnie z ostatnich równań ma postać daną wzorem (10. 2), jeśli. Rozwiązanie (10. 3) jest rozwiązaniem niefizycznym. Musimy więc wziąć albo część urojoną tego równania, albo część rzeczywistą. 10. 1. 1 Człony nieliniowe w równaniu oscylatora harmonicznego W dotychczasowym rozwiązaniu równania oscylatora harmonicznego założyliśmy że wychylenia są tak małe, że możemy napisać sin . Jeśli tak nie jest , musimy uwzględnić dalsze człony w rozwinięciu funkcji sinus. . 15. 12. 2008 Reinhard Kulessa 8

Równanie (10. 2) przyjmuje wtedy postać: . (10. 4) Jest to równanie ruchu oscylatora anharmonicznego. Przewidujemy rozwiązanie postaci; . Podstawiając to wyrażenie do równania (10. 4), zaniedbując człony z 2 oraz 3, oraz korzystając z tożsamości , Stwierdzamy, że podane jest rozwiązaniem naszego równania pod warunkiem, że 15. 12. 2008 Reinhard Kulessa 9

. Ostatnie równanie można przybliżyć wyrażeniem; . (10. 5) Nie rozważając pozostałych członów, z których można wyliczyć np. , widzimy, że w 0 gdy 0 w zależy od amplitudy dla dużych amplitud. Należy również zaznaczyć, że w ruchu wahadła występują tylko nieparzyste harmoniczne. 15. 12. 2008 Reinhard Kulessa 10

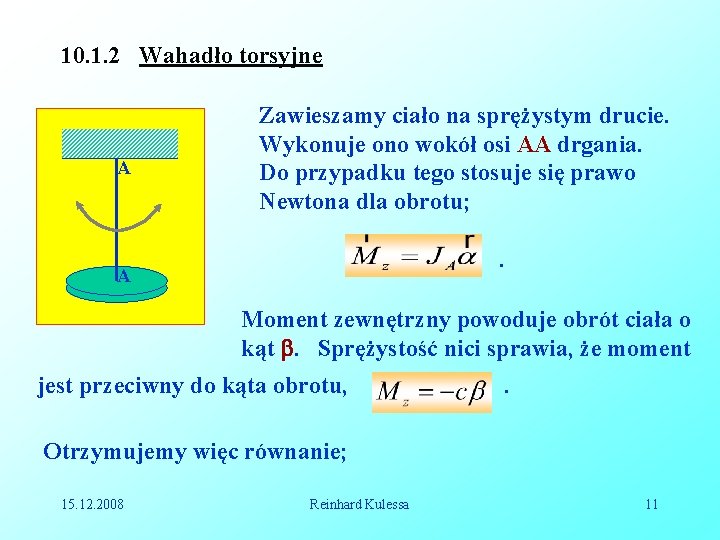
10. 1. 2 Wahadło torsyjne A Zawieszamy ciało na sprężystym drucie. Wykonuje ono wokół osi AA drgania. Do przypadku tego stosuje się prawo Newtona dla obrotu; . A Moment zewnętrzny powoduje obrót ciała o kąt . Sprężystość nici sprawia, że moment jest przeciwny do kąta obrotu, . Otrzymujemy więc równanie; 15. 12. 2008 Reinhard Kulessa 11

. Równanie to ma rozwiązanie: . Z ostatniego równania widać, że w oparciu o ostatnie równanie można wyznaczyć moment bezwładności zawieszonego ciała. 15. 12. 2008 Reinhard Kulessa 12

10. 1. 3 „Ciekłe” wahadło y y l Jeśli rurkę o kształcie U i stałym przekroju S napełnimy cieczą o gęstości , ustala się po pewnym czasie równowaga dla której poziom cieczy określa linia przerywana. Słup cieczy w kształcie litery U ma długość l. Jeśli w jednej rurce przesuniemy o y poziom cieczy, powstaje różnica poziomów 2 y między rurkami. Ciężar wystającego słupa cieczy o masie m 2 y powoduje pojawienie się siły zwrotnej. Zgodnie z prawem Newtona mamy; . 15. 12. 2008 Reinhard Kulessa 13

Nadmiarowa masa wynosi; . Równanie różniczkowe dla drgającej cieczy ma postać, . Rozwiązanie tego równania jest następujące; . 15. 12. 2008 Reinhard Kulessa 14

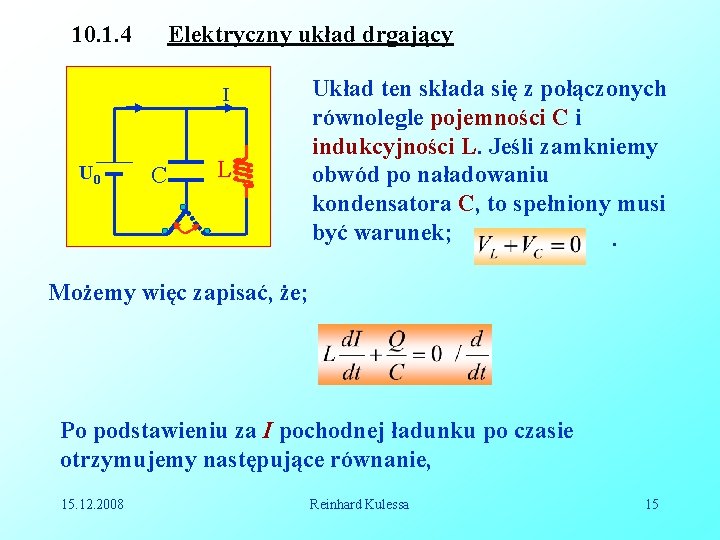
10. 1. 4 Elektryczny układ drgający I U 0 C L Układ ten składa się z połączonych równolegle pojemności C i indukcyjności L. Jeśli zamkniemy obwód po naładowaniu kondensatora C, to spełniony musi być warunek; . Możemy więc zapisać, że; Po podstawieniu za I pochodnej ładunku po czasie otrzymujemy następujące równanie, 15. 12. 2008 Reinhard Kulessa 15

. Jest to równanie oscylatora harmonicznego o częstości. 15. 12. 2008 Reinhard Kulessa 16

10. 1. 5 Średnia energia swobodnego oscylatora harmonicznego Z rozwiązania równania (10. 1) otrzymujemy; Średnia energia kinetyczna przypadająca na jeden okres wynosi; . 15. 12. 2008 Reinhard Kulessa 17

Policzmy z kolei średnią energię potencjalną; . Przy czym . Całkowita energia oscylatora harmonicznego wynosi; . 15. 12. 2008 Reinhard Kulessa (10. 6) 18

10. 1. 6 Wpływ tarcia na ruch Jeżeli tarcie jest jedyną siłą, która wpływa na ruch, to. Zwykle przyjmuje się, że siła tarcia jest proporcjonalna do prędkości ciała. . Równanie ruchu jest wtedy następujące: Wielkość m/ nazywamy stałą relaksacji . 15. 12. 2008 Reinhard Kulessa 19

Równanie ruchu możemy przekształcić do postaci; . Rozwiązaniem tego równania jest funkcja; . l jest stałą zaniku równą odwrotności czasu relaksacji. Zależność energii kinetycznej od czasu ma postać; . 15. 12. 2008 Reinhard Kulessa 20

10. 2 Oscylator harmoniczny tłumiony Jeżeli uwzględnimy oprócz siły napędzającej oscylator harmoniczny również siły oporu np. proporcjonalne do prędkości, to równanie oscylatora przyjmuje postać; . Po wprowadzeniu oznaczeń otrzymujemy równanie; . (10. 7) oznacza stałą relaksacji. 15. 12. 2008 Reinhard Kulessa 21

Rozwiązania tego równania szukamy w postaci; . Policzmy odpowiednie pochodne i znajdźmy warunki, dla których równanie to jest spełnione. . Po podstawieniu tych wartości do równania (10. 7) otrzymamy następujące równanie; . 15. 12. 2008 Reinhard Kulessa 22

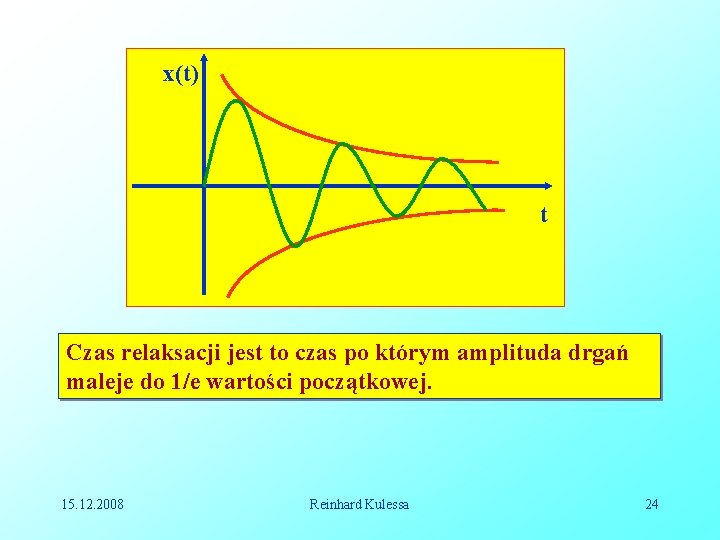
Równanie to ma rozwiązanie gdy współczynniki przy sin t i cos t się zerują, czyli dla. . Widzimy, że częstość oscylatora tłumionego zależy od parametru tłumienia. Ogólne rozwiązanie na amplitudę drgań oscylatora tłumionego ma postać; . (10. 8) Czasowy przebieg amplitudy jest następujący; 15. 12. 2008 Reinhard Kulessa 23

x(t) t Czas relaksacji jest to czas po którym amplituda drgań maleje do 1/e wartości początkowej. 15. 12. 2008 Reinhard Kulessa 24

10. 3 Współczynnik dobroci oscylatora harmonicznego Dla układów drgających, a w szczególności elektrycznych mówi się często o współczynniku dobroci Q. Współczynnik ten definiuje się jako odwrotność względnej straty energii przypadającej na jeden okres. Można pokazać, że dla oscylatora harmonicznego tłumionego drgającego zgodnie z równaniem (10. 8) jest dla przypadku gdy 0 >> 1 dane przez; . 15. 12. 2008 Reinhard Kulessa 25
 Stochastic fast
Stochastic fast Oscylator paul
Oscylator paul Różnica elektroujemności
Różnica elektroujemności Ruch krzywoliniowy
Ruch krzywoliniowy Ruch drgający harmoniczny wielkości charakteryzujące
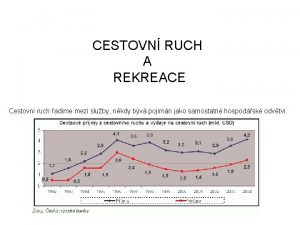
Ruch drgający harmoniczny wielkości charakteryzujące Udržitelný cestovní ruch definice
Udržitelný cestovní ruch definice Ruch harmoniczny prosty
Ruch harmoniczny prosty Oprogramowanie śledzące ruch myszką
Oprogramowanie śledzące ruch myszką Ruch harmoniczny prosty
Ruch harmoniczny prosty Výjezdový cestovní ruch
Výjezdový cestovní ruch Dział mechaniki klasycznej
Dział mechaniki klasycznej Wzory na ruch
Wzory na ruch Ruch laminarny
Ruch laminarny Ruch to zdrowie prezentacja
Ruch to zdrowie prezentacja Prędkość liniowa
Prędkość liniowa Przyczyny kontrreformacji
Przyczyny kontrreformacji Kinematyka wzory
Kinematyka wzory Model ruchu okrężnego w gospodarce otwartej
Model ruchu okrężnego w gospodarce otwartej Punkt na sferze niebieskiej
Punkt na sferze niebieskiej Cestovní ruch pracovní list
Cestovní ruch pracovní list Ruch falowy definicja
Ruch falowy definicja Vincent ruch
Vincent ruch Jak obliczyć wartość przyspieszenia
Jak obliczyć wartość przyspieszenia