Wykad IV Ruch harmoniczny Ruch harmoniczny prosty m













- Slides: 33

Wykład IV Ruch harmoniczny

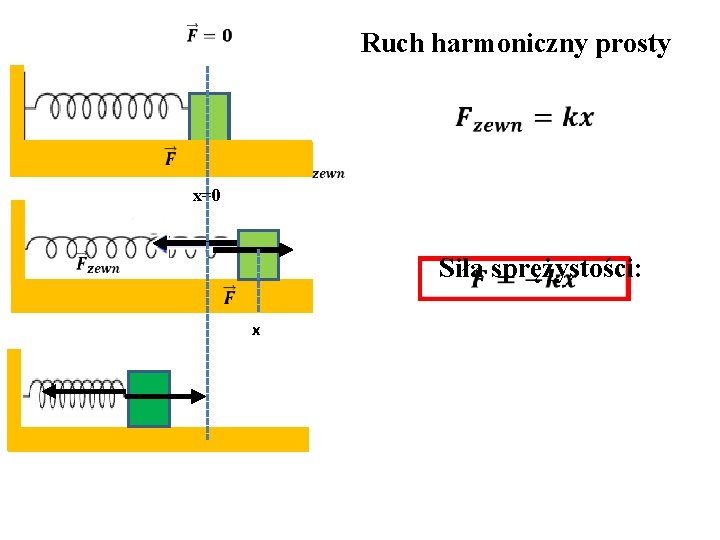
Ruch harmoniczny prosty m 0 x=0 Siła sprężystości: x

Ruch harmoniczny prosty Równanie ruchu w dowolnej chwili m x równanie różniczkowe na x(t)!

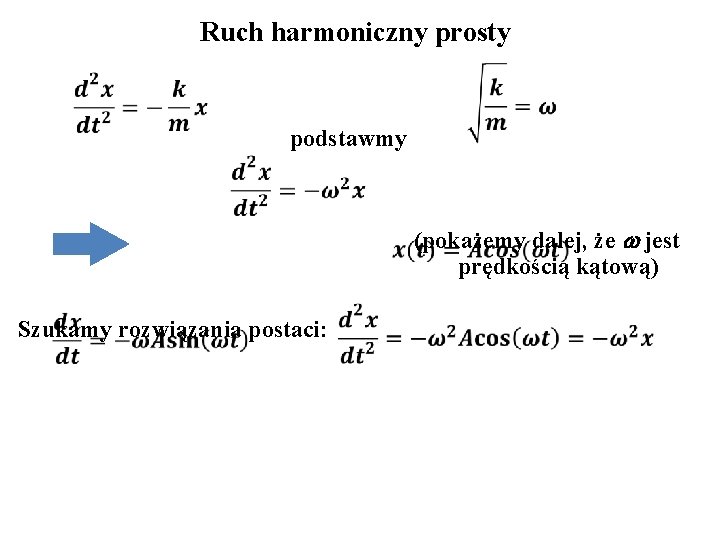
Ruch harmoniczny prosty podstawmy (pokażemy dalej, że w jest prędkością kątową) Szukamy rozwiązania postaci:

Parametry: okres drgań Definicja okresu T: czas, po którym faza drgania jest taka sama Wzór potwierdza słuszność założenia, że to prędkość kątowa. Aby to pokazać, opiszemy ruchu po okręgu.

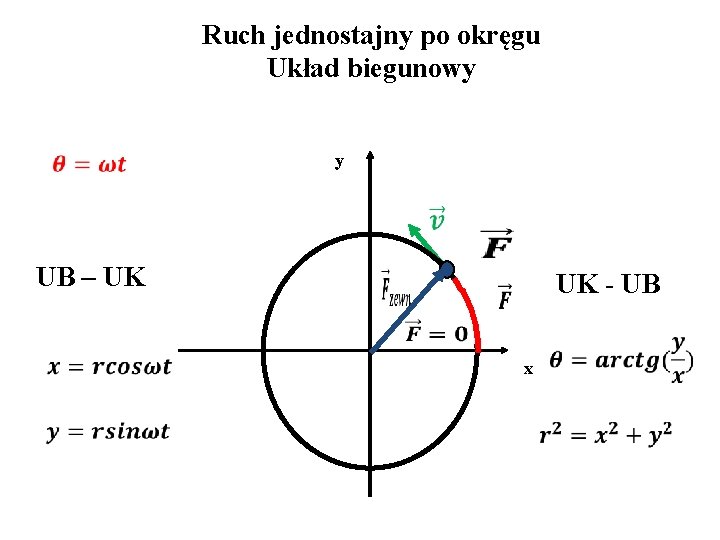
Ruch jednostajny po okręgu Układ biegunowy y UB – UK UK - UB x

Współrzędne biegunowe W układzie biegunowym prędkość kątowa y Wówczas v = r wektorowo: x

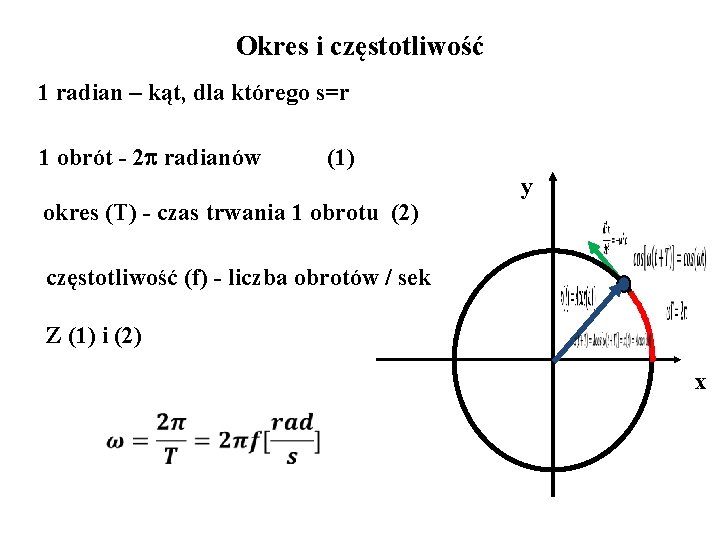
Okres i częstotliwość 1 radian – kąt, dla którego s=r 1 obrót - 2 radianów (1) okres (T) - czas trwania 1 obrotu (2) y częstotliwość (f) - liczba obrotów / sek Z (1) i (2) x

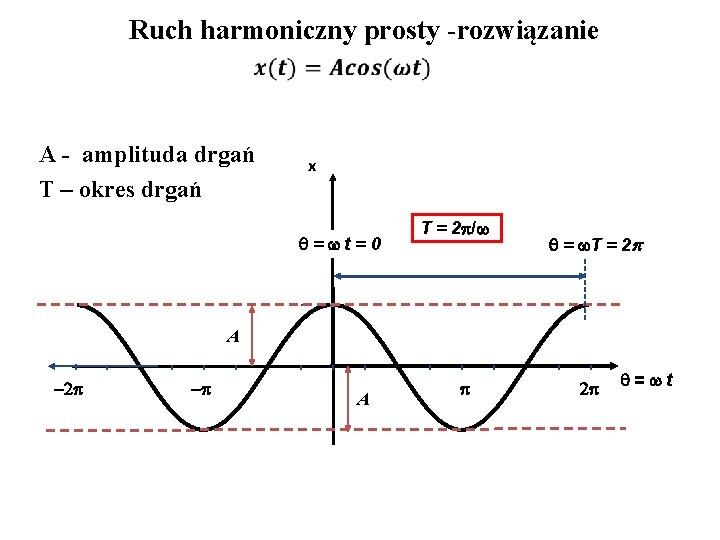
Ruch harmoniczny prosty -rozwiązanie A - amplituda drgań T – okres drgań x = t=0 T = 2 / = T = 2 p A = t

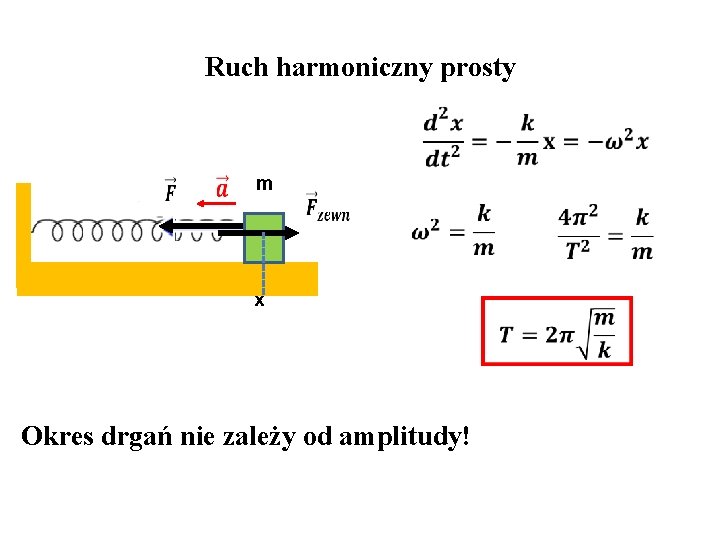
Ruch harmoniczny prosty m x Okres drgań nie zależy od amplitudy!

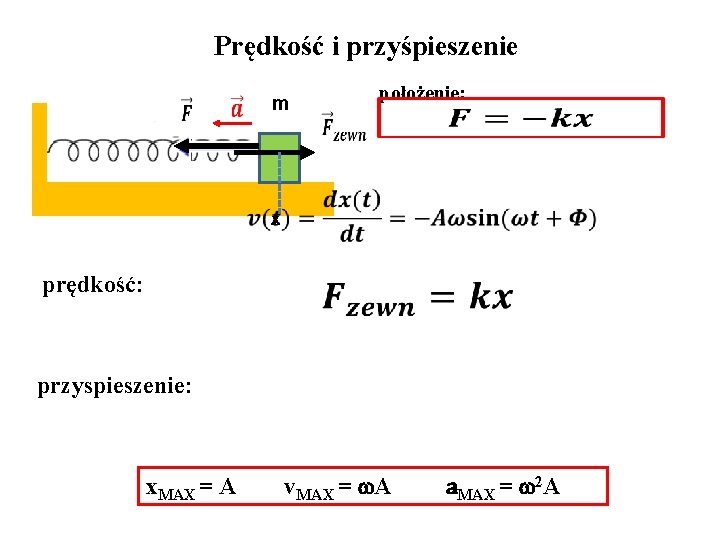
Prędkość i przyśpieszenie m położenie: x prędkość: przyspieszenie: x. MAX = A v. MAX = A a. MAX = 2 A

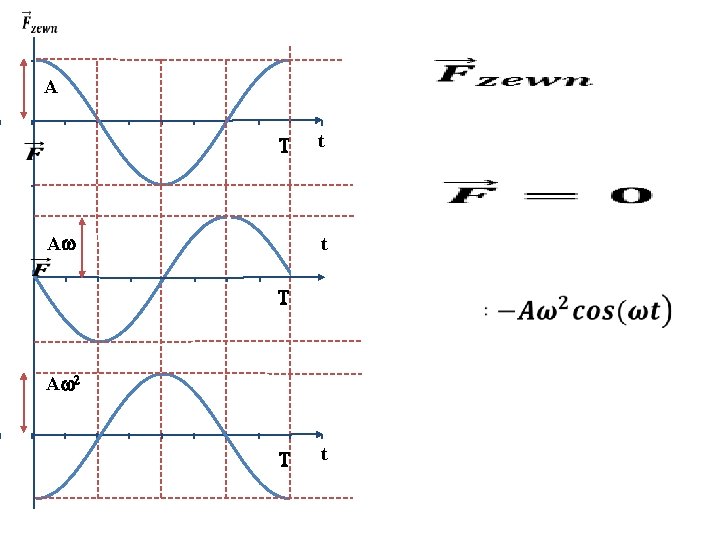
A T t t A T A T t

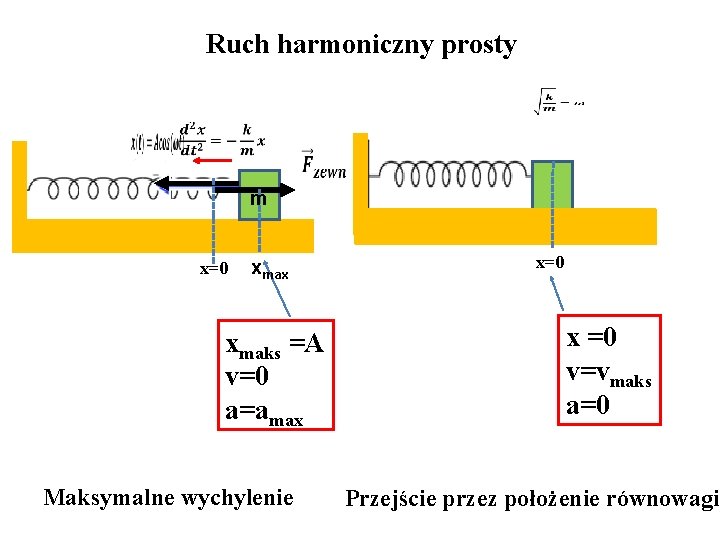
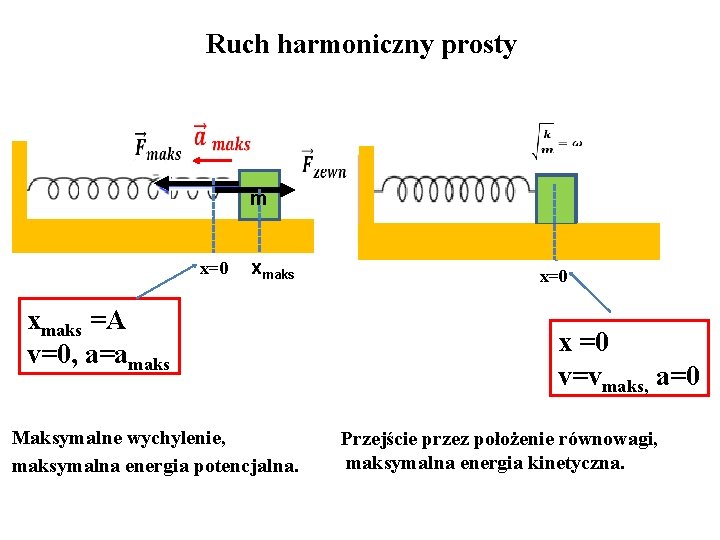
Ruch harmoniczny prosty m x=0 xmax xmaks =A v=0 a=amax Maksymalne wychylenie m x=0 x =0 v=vmaks a=0 Przejście przez położenie równowagi

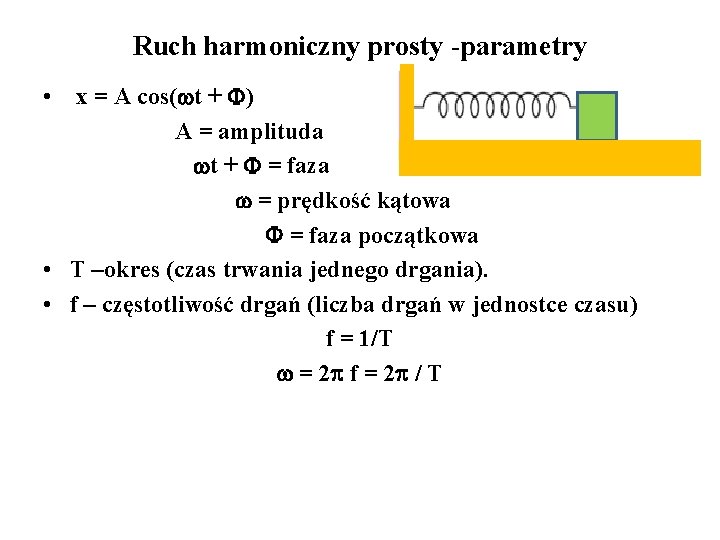
Ruch harmoniczny prosty -parametry • x = A cos( t + F) A = amplituda t + F = faza = prędkość kątowa F = faza początkowa • T –okres (czas trwania jednego drgania). • f – częstotliwość drgań (liczba drgań w jednostce czasu) f = 1/T = 2 f = 2 / T

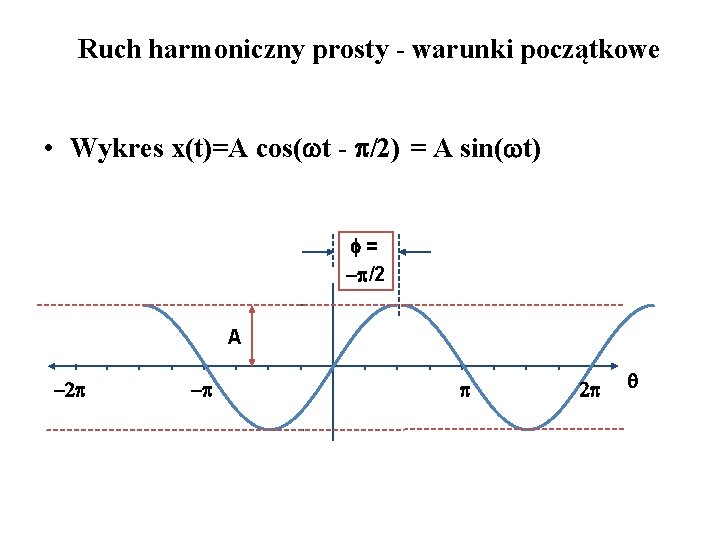
Ruch harmoniczny prosty - warunki początkowe • Wykres x(t)=A cos( t - /2) = A sin( t) = /2 A

Warunki początkowe –przykład cd. dla = - /2 x(t) = A cos( t - /2 ) v(t) = - A sin( t - /2 ) a(t) = - 2 A cos( t - /2 ) x(t) = A sin( t) v(t) = A cos( t) a(t) = - 2 A sin( t) x(t) A x(t) -A t

Ruch harmoniczny prosty - energia

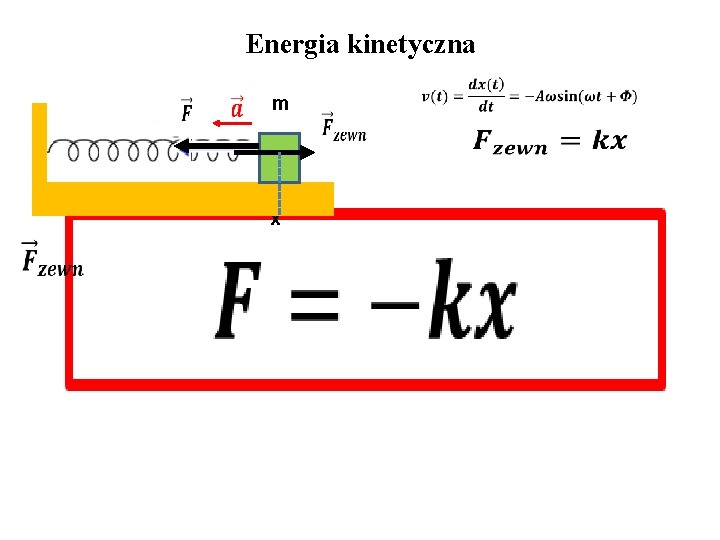
Energia kinetyczna m x

Energia potencjalna m x

E(t) E Ep(t) Ek(t) T E=Ep(t)+Ek(t) t

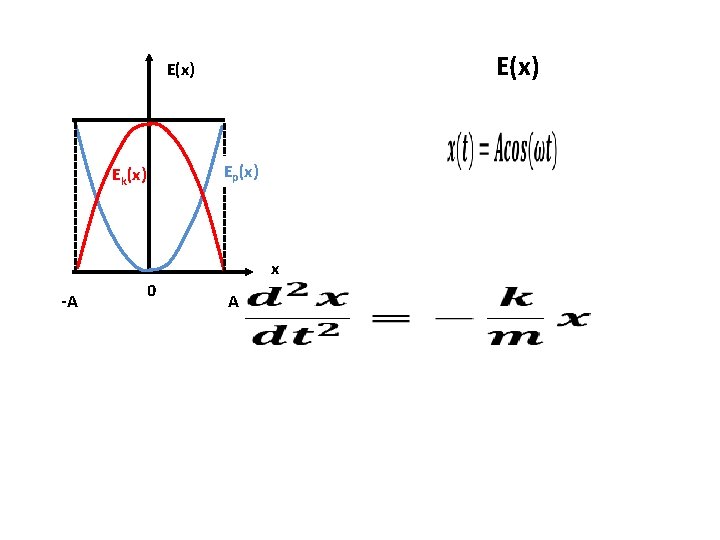
E(x) Ep(x) Ek(x) -A 0 x A

Ruch harmoniczny prosty m x=0 xmaks =A v=0, a=amaks Maksymalne wychylenie, maksymalna energia potencjalna. m x=0 x =0 v=vmaks, a=0 Przejście przez położenie równowagi, maksymalna energia kinetyczna.

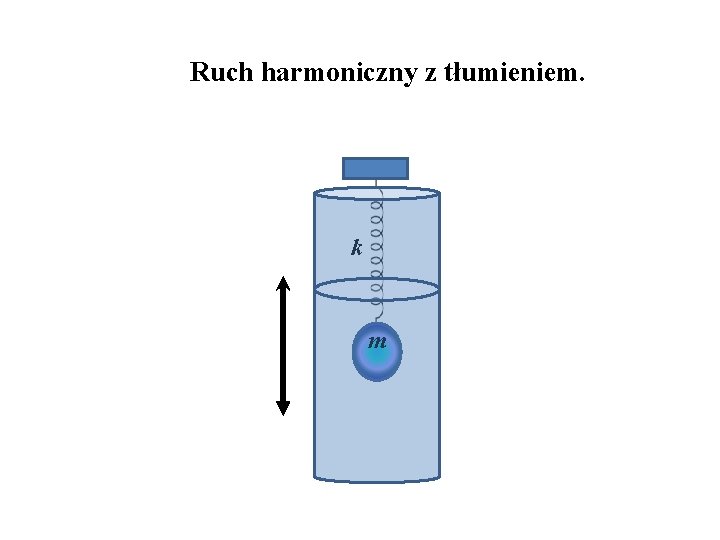
Ruch harmoniczny z tłumieniem. k m

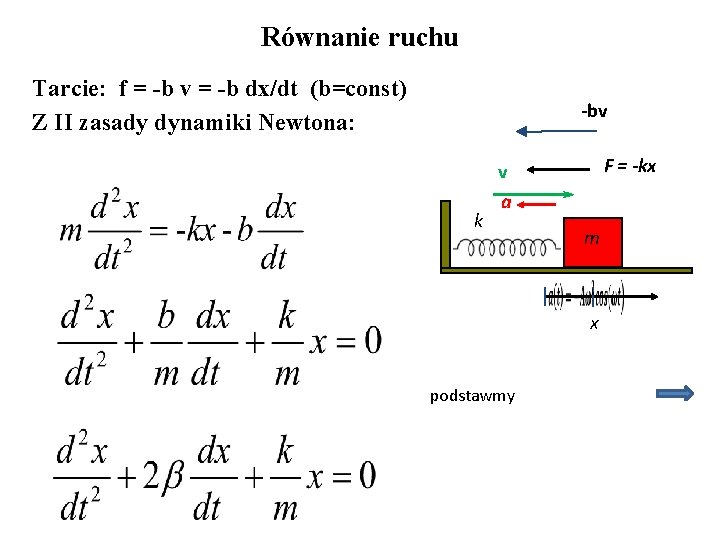
Równanie ruchu Tarcie: f = -b v = -b dx/dt (b=const) Z II zasady dynamiki Newtona: -bv k F = -kx v a m x podstawmy

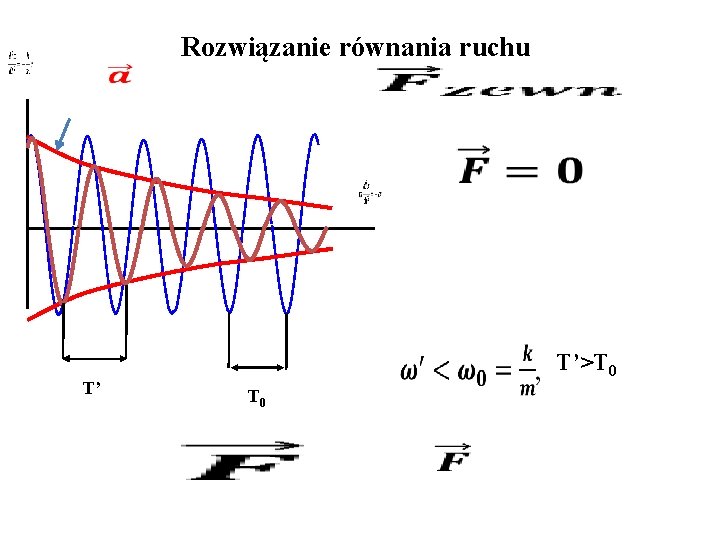
Rozwiązanie równania ruchu T’ T’>T 0

Logarytmiczny dekrement tłumienia

Ruch harmoniczny z tłumieniem – energia mechaniczna E(t) Bez tłumienia: E = 1/2 k A 2 = const Z tłumieniem: E(t) = 1/2 k. A(t)2 = 1/2 k A 2 exp(-2 bt) W ruchu harmonicznym z tłumieniem, całkowita energia mechaniczna maleje wykładniczo z czasem

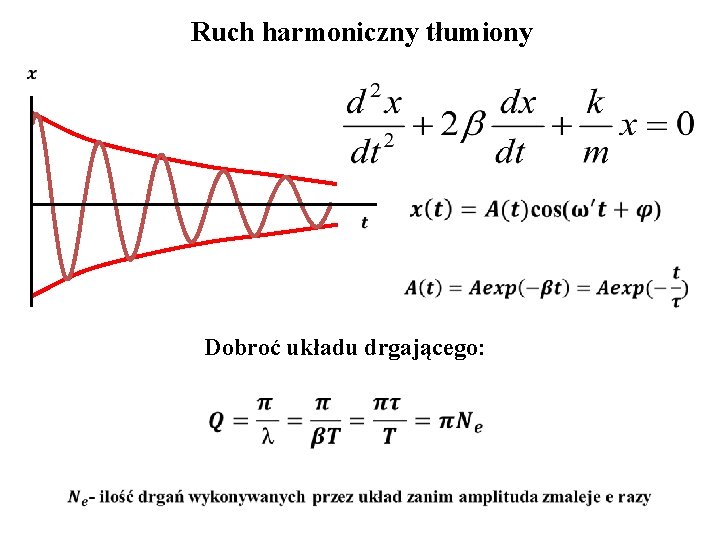
Ruch harmoniczny tłumiony Dobroć układu drgającego:

Ruch harmoniczny z tłumieniem i silą wymuszającą x(t) = A cos( wymt + )

Rezonans mechaniczny

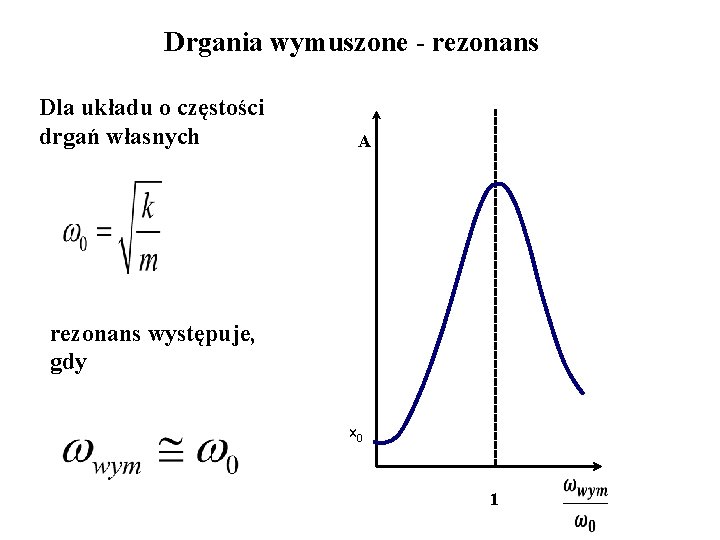
Drgania wymuszone - rezonans Dla układu o częstości drgań własnych A rezonans występuje, gdy x 0 1

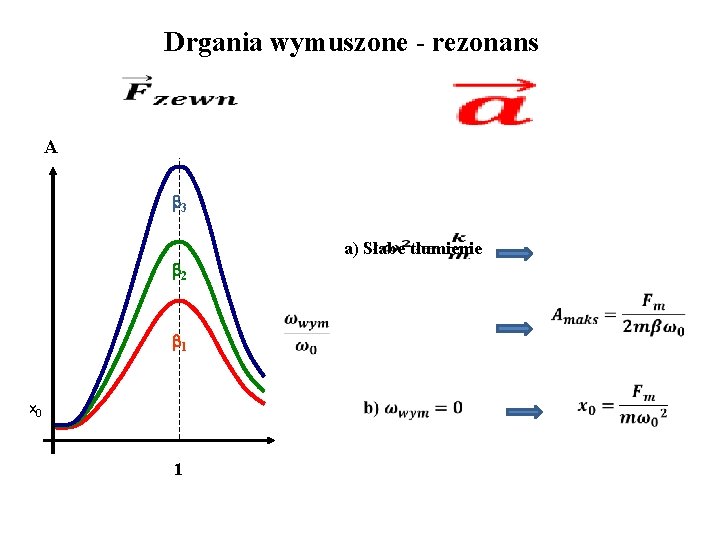
Drgania wymuszone - rezonans A b 3 b 2 b 1 x 0 1 a) Słabe tłumienie

Dobroć układu rezonansowego Dla słabego tłumienia, stosunek amplitudy, którą ma układ dla częstotliwości rezonansowej do wychylenia z położenia równowagi pod wpływem siły równej amplitudzie siły wymuszającej jest równy dobroci układu rezonansowego: Podczas rezonansu siła wymuszająca jest w fazie z prędkością, ponieważ wówczas moc tej siły osiąga największą wartość:
 Ruch harmoniczny prosty
Ruch harmoniczny prosty Ruch harmoniczny prosty
Ruch harmoniczny prosty Ruch drgający harmoniczny wielkości charakteryzujące
Ruch drgający harmoniczny wielkości charakteryzujące Oscylator harmoniczny wzory
Oscylator harmoniczny wzory Kwantowy oscylator harmoniczny
Kwantowy oscylator harmoniczny Graniastosłup którego wszystkie ściany są kwadratami to
Graniastosłup którego wszystkie ściany są kwadratami to Objętości figur
Objętości figur Graniastosłup pochyły siatka
Graniastosłup pochyły siatka Metoda nkp
Metoda nkp Front przeladunkowy
Front przeladunkowy Produkt turystyczny prosty
Produkt turystyczny prosty Ile ma wierzchołków graniastosłup pięciokątny
Ile ma wierzchołków graniastosłup pięciokątny Siatka graniastosłupa czworokątnego
Siatka graniastosłupa czworokątnego Popis prostý
Popis prostý Siad klęczny zakroczny
Siad klęczny zakroczny Ruch krzywoliniowy
Ruch krzywoliniowy Zadania na ruch jednostajnie przyspieszony
Zadania na ruch jednostajnie przyspieszony Punkt na sferze niebieskiej
Punkt na sferze niebieskiej Ruch falowy definicja
Ruch falowy definicja Ruch laminarny
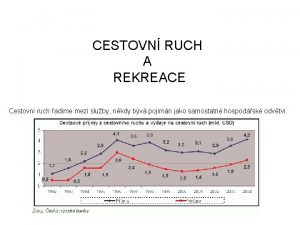
Ruch laminarny Výjezdový cestovní ruch
Výjezdový cestovní ruch Ruch jednostajnie przyspieszony
Ruch jednostajnie przyspieszony Dział mechaniki klasycznej
Dział mechaniki klasycznej Udržitelný cestovní ruch definice
Udržitelný cestovní ruch definice Model ruchu okrężnego w gospodarce otwartej
Model ruchu okrężnego w gospodarce otwartej Ruch kontrreformacyjny
Ruch kontrreformacyjny Oprogramowanie śledzące ruch myszką
Oprogramowanie śledzące ruch myszką Cestovní ruch pracovní list
Cestovní ruch pracovní list Kinematyka wzory
Kinematyka wzory Wiinom plan
Wiinom plan Ruch to zdrowie prezentacja dla dzieci
Ruch to zdrowie prezentacja dla dzieci Przyspieszenie styczne i normalne
Przyspieszenie styczne i normalne