DRGANIA Ruch harmoniczny prosty tumiony drgania wymuszone Ruch












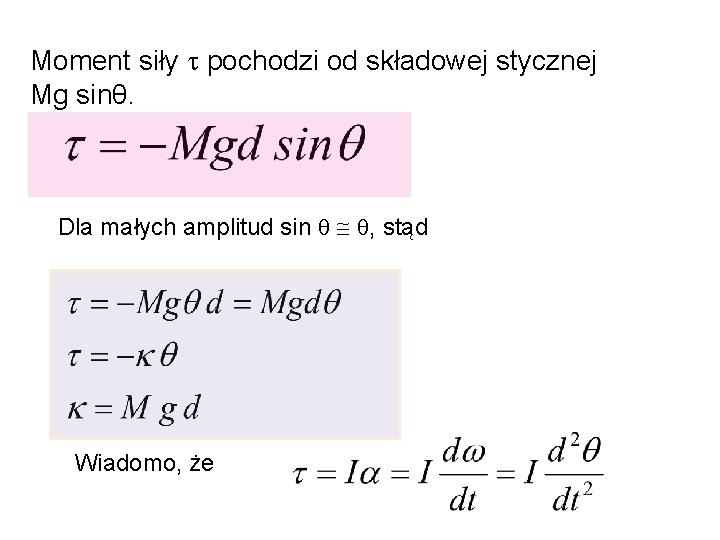











- Slides: 34

DRGANIA Ruch harmoniczny, prosty, tłumiony, drgania wymuszone

Ruch harmoniczny Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym. Przemieszczenie cząstki w ruchu okresowym można wyrazić za pomocą funkcji sinus lub cosinus. Funkcje te nazywamy funkcjami harmonicznymi, stąd ruch okresowy cząstki nazywany jest ruchem harmonicznym. Ruchem drgającym mogą poruszać się nie tylko układy mechaniczne, ale również cząsteczki obdarzone ładunkiem elektrycznym i fale elektromagnetyczne. W przypadku fal elektromagnetycznych występują drgania wektora pola magnetycznego oraz elektrycznego.

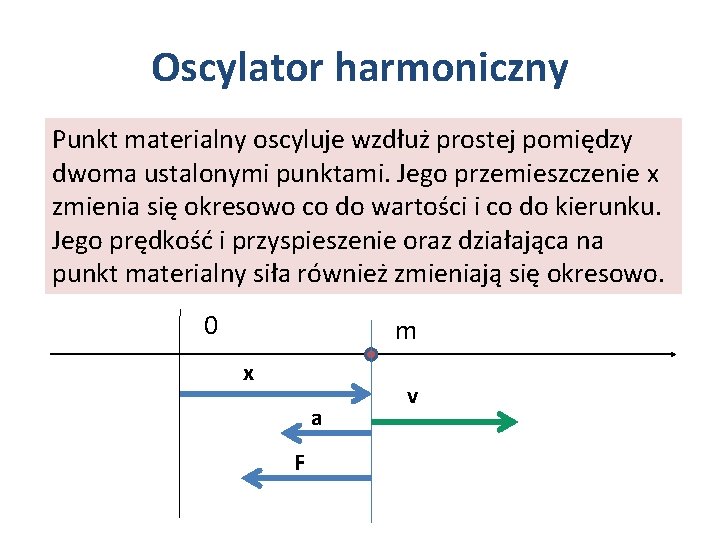
Oscylator harmoniczny Punkt materialny oscyluje wzdłuż prostej pomiędzy dwoma ustalonymi punktami. Jego przemieszczenie x zmienia się okresowo co do wartości i co do kierunku. Jego prędkość i przyspieszenie oraz działająca na punkt materialny siła również zmieniają się okresowo. 0 m x a F v

Ruch harmoniczny prosty Całkowita energia drgającego punktu jest sumą jego energii kinetycznej i potencjalnej: E=K +U Zakładamy, że ciało porusza się po płaszczyźnie poziomej bez tarcia oraz że spełnione jest prawo Hooke’a, wówczas siła i wychylenie powiązane są zależnością: F = - kx Energia potencjalna wynosi:

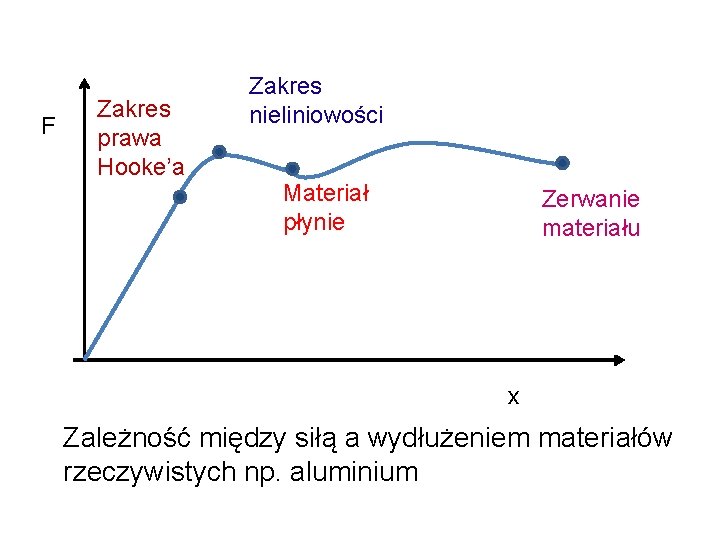
F Zakres prawa Hooke’a Zakres nieliniowości Materiał płynie Zerwanie materiału x Zależność między siłą a wydłużeniem materiałów rzeczywistych np. aluminium

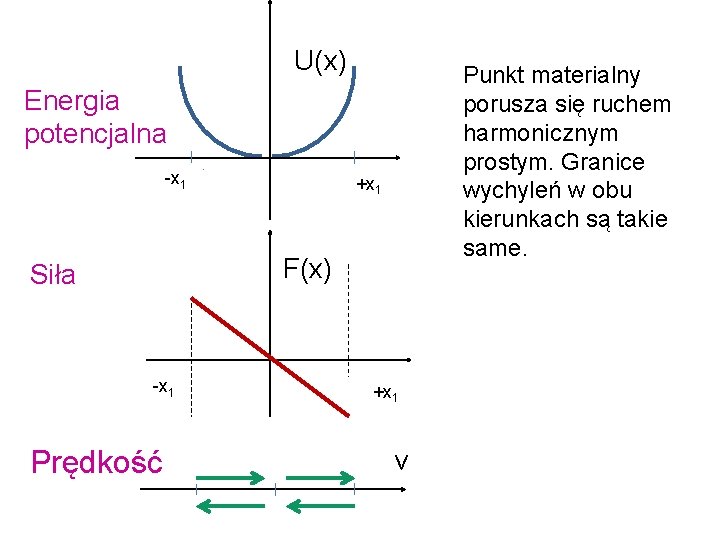
U(x) Punkt materialny porusza się ruchem harmonicznym prostym. Granice wychyleń w obu kierunkach są takie same. Energia potencjalna -x 1 +x 1 F(x) Siła -x 1 Prędkość +x 1 v

Okresem ruchu harmonicznego T jest czas jednego pełnego drgnięcia albo cyklu. Jest to najkrótszy czas po upływie którego ruch zaczyna się powtarzać. Częstością jest liczba drgań w jednostce czasu. Jednostką częstotliwości jest 1 Hz.

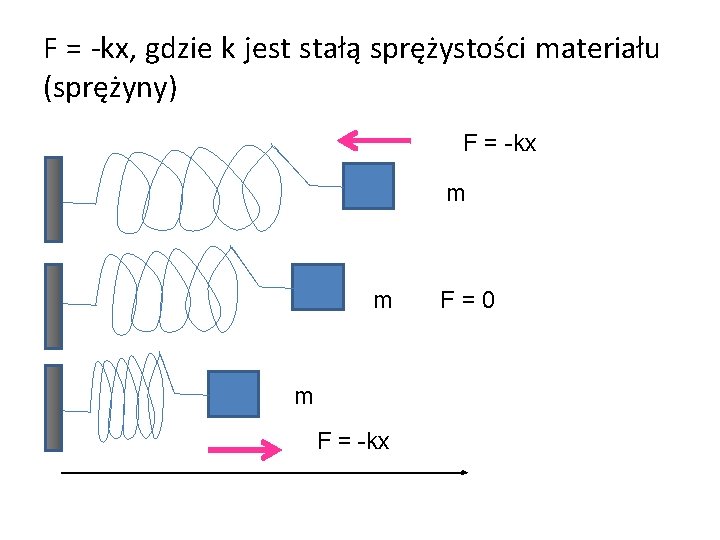
F = -kx, gdzie k jest stałą sprężystości materiału (sprężyny) F = -kx m m m F = -kx F=0

II Zasada Newtona dla ruchu sprężyny: F = ma F = - kx Otrzymaliśmy równanie różniczkowe, którego rozwiązaniem jest x(t) – funkcja czasu. Rozwiązaniem tego równania jest funkcja sinus i cosinus.

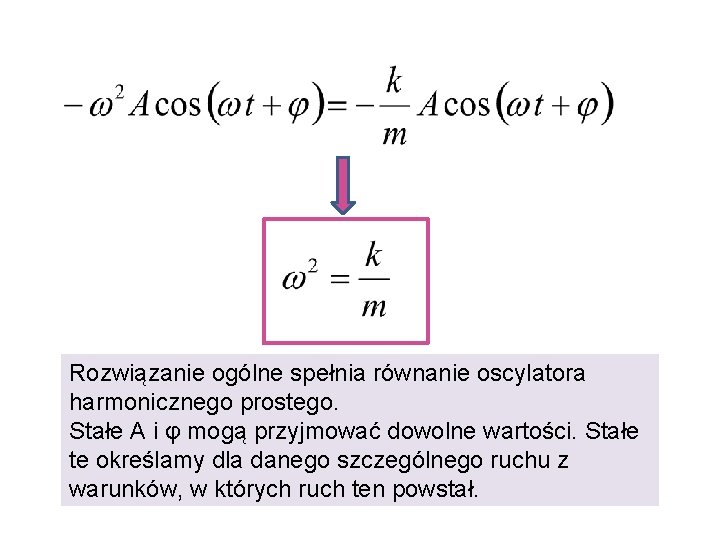
Rozwiązanie ogólne tego równania: Rozwiązanie to oraz jego drugą pochodną wstawiamy do równania. - Faza początkowa

Rozwiązanie ogólne spełnia równanie oscylatora harmonicznego prostego. Stałe A i φ mogą przyjmować dowolne wartości. Stałe te określamy dla danego szczególnego ruchu z warunków, w których ruch ten powstał.

A x t T v a t

Wahadło proste l T M Mg cos Mg sin Mg Wyidealizowane ciało o masie punktowej M, zawieszone na cienkiej, nierozciągliwej nici o długości l. Wytrącone z równowagi zaczyna się wahać w płaszczyźnie poziomej pod wpływem siły ciężkości.

Składowa styczna przywracająca równowagę: F = -Mg sin nie jest proporcjonalna do wychylenia. Przemieszczenie wzdłuż łuku: x=lθ dla małych kątów sinθ θ w mierze łukowej Dla małych przemieszczeń siła F jest proporcjonalna do wychylenia ze znakiem przeciwnym. Ruch harmoniczny prosty

określa stałą k w równaniu F = -kx Okres dla małych amplitud: Okres wahadła prostego nie zależy od masy wahadła.

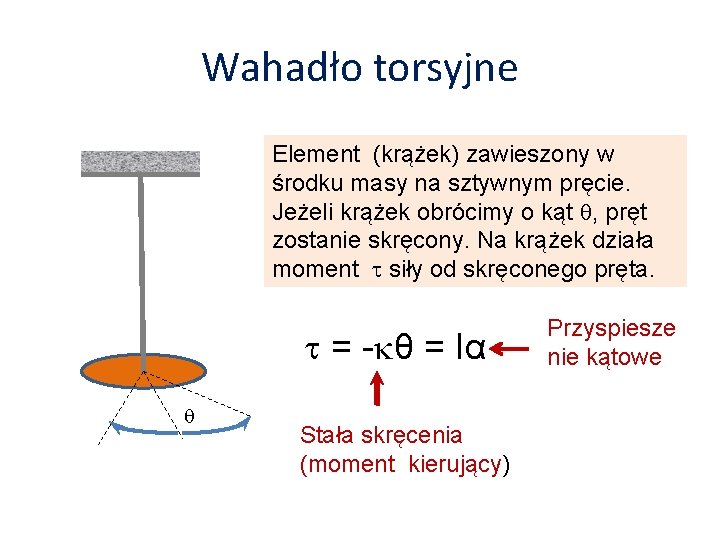
Wahadło torsyjne Element (krążek) zawieszony w środku masy na sztywnym pręcie. Jeżeli krążek obrócimy o kąt , pręt zostanie skręcony. Na krążek działa moment siły od skręconego pręta. = - θ = Iα Stała skręcenia (moment kierujący) Przyspiesze nie kątowe

W ruchu obrotowym moment siły zależy od przyspieszenia kątowego α = Iα I – moment bezwładności Równanie ruchu układu: gdzie ω – prędkość kątowa Otrzymane zostało równanie dla kątowego ruchu harmonicznego.

Otrzymane równanie jest podobne do równania liniowego ruchu harmonicznego prostego. x→θ M→I k→ Rozwiązanie tego równania ma postać: gdzie m jest amplitudą wychylenia kątowego Φ – fazą dla t = 0

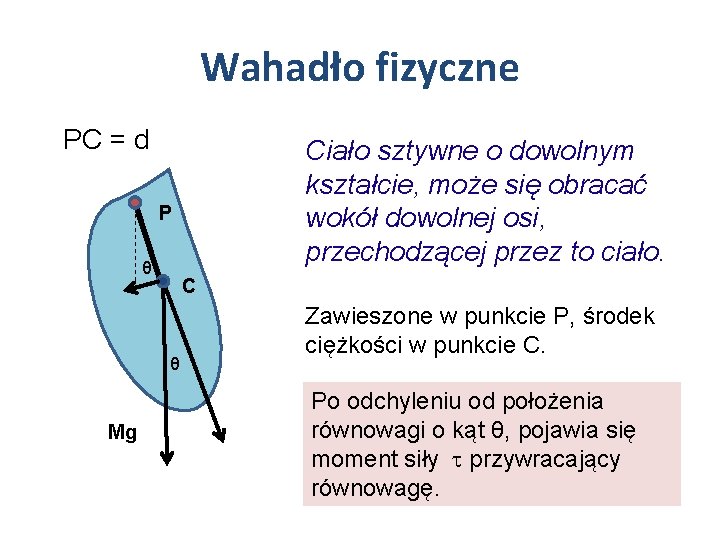
Wahadło fizyczne PC = d Ciało sztywne o dowolnym kształcie, może się obracać wokół dowolnej osi, przechodzącej przez to ciało. P θ C θ Mg Zawieszone w punkcie P, środek ciężkości w punkcie C. Po odchyleniu od położenia równowagi o kąt θ, pojawia się moment siły przywracający równowagę.
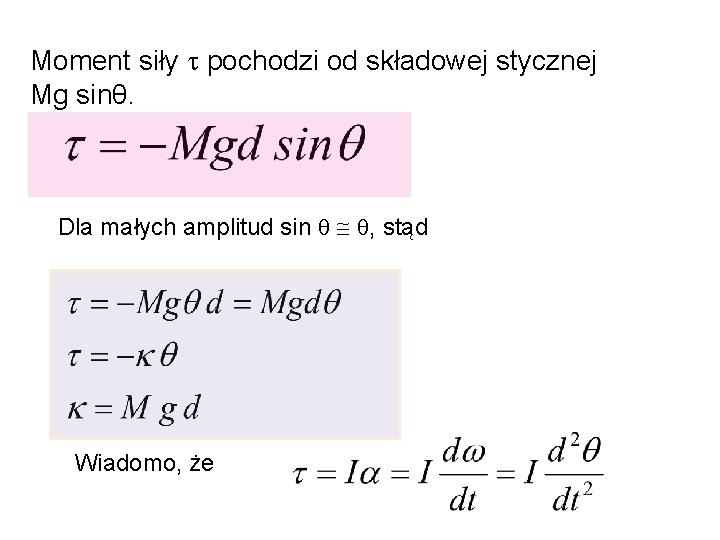
Moment siły pochodzi od składowej stycznej Mg sinθ. Dla małych amplitud sin , stąd Wiadomo, że

Z poprzednich związków wynika, że Rozwiązaniem tego równania jest funkcja czasu θ = f(t) o postaci na przykład: = sinωt, gdzie ω jest pulsacją ruchu okresowego. Rozwiązując to równanie otrzymujemy tak zwane równanie charakterystyczne o postaci:

- jest częstotliwością, T – okresem drgań Wahadło fizyczne wykonuje ruch okresowy, ale nie jest to prosty ruch harmoniczny. Okres T tego ruchu zależy od momentu bezwładności ciała, jego masy, odległości osi obrotu od środka ciężkości i przyspieszenia ziemskiego.

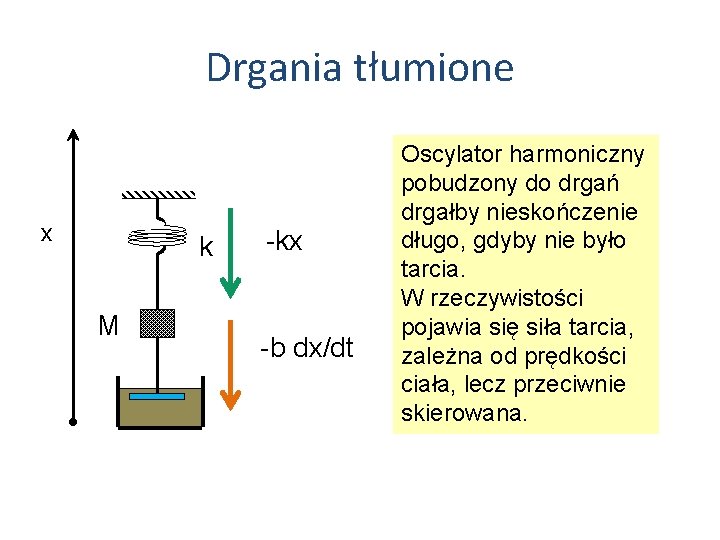
Drgania tłumione x k M m -kx -b dx/dt Oscylator harmoniczny pobudzony do drgań drgałby nieskończenie długo, gdyby nie było tarcia. W rzeczywistości pojawia się siła tarcia, zależna od prędkości ciała, lecz przeciwnie skierowana.

Równanie ruchu oscylatora harmonicznego z uwzględnieniem siły tarcia: Jest to równanie oscylatora harmonicznego tłumionego o stałej tłumienia b.

Rozwiązaniem tego równania dla przypadku małej wartości stałej b jest zależność x od czasu: A – amplituda oscylacji Tarcie powoduje spowolnienie ruchu, zmniejszenie częstotliwości i wydłużenie okresu drgań. Przy bardzo dużym tarciu następuje zanik oscylacji.

+A x T -A Wykres ruchu harmonicznego tłumionego t

Drgania wymuszone i rezonans W przypadku wszystkich omawianych dotychczas drgań, pobudzenie było jednorazowe – wychylenie ciała ze stanu równowagi i następnie puszczenie swobodne tego ciała. Ciało wykonywało drgania, bądź tylko jednorazowo się wychylało (duże tłumieni). Drgania po pewnym czasie zanikały w wyniku tarcia. Teoretyczny rezonator harmoniczny wykonuje drgania nieskończenie długo, bo pomijamy tłumienie w wyidealizowanym modelu.

Drgania mogą być podtrzymywane w wyniku dodania siły działającej okresowo. Drgania takie nazywamy wymuszonymi. Układ drga wówczas z częstotliwością siły pobudzającej F. Fm – maksymalna wartość siły ω’’ – częstość kołowa siły wymuszającej ω’’ = 2π ’’

Równanie ruchu : lub Rozwiązaniem tego równania jest funkcja czasu:

gdzie ω – jest częstością kołową drgań własnych układu Otrzymana postać rozwiązania wskazuje na to, że maksymalną amplitudę drgań otrzymamy przy częstotliwości siły pobudzającej równej częstotliwości drgań własnych.

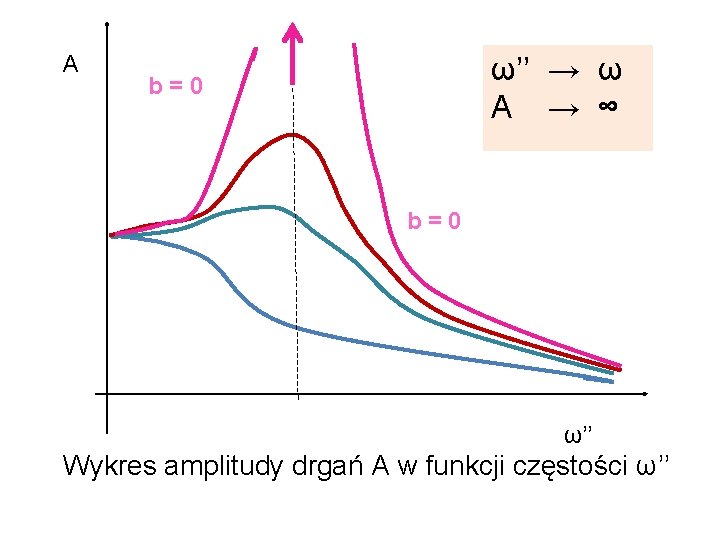
A ω’’ → ω A → ∞ b=0 ω’’ Wykres amplitudy drgań A w funkcji częstości ω’’

Dla oscylatorów tłumionych przy pewnej charakterystycznej częstotliwości wymuszającej ω’’amplituda oscylacji osiąga maksimum. Takie zjawisko nazywamy rezonansem, a częstotliwość odpowiednio – częstotliwością rezonansową. Im mniejsze tłumienie tym częstotliwość rezonansowa jest bliższa częstotliwości ω układu nietłumionego.

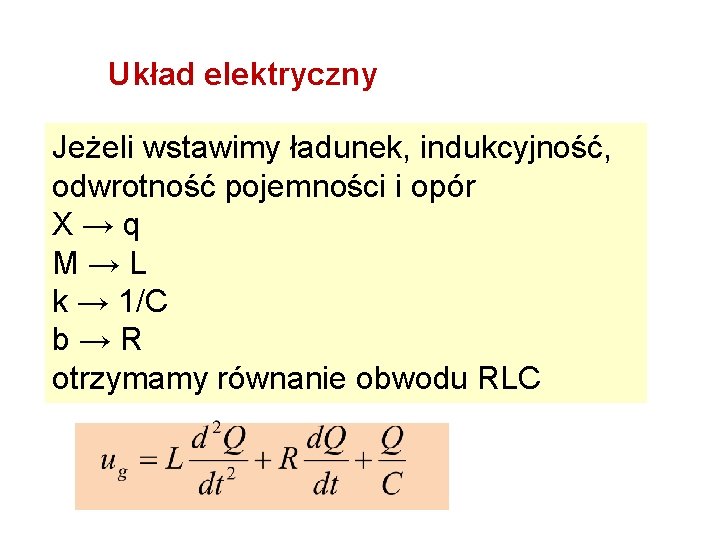
Układ elektryczny Jeżeli wstawimy ładunek, indukcyjność, odwrotność pojemności i opór X→q M→L k → 1/C b→R otrzymamy równanie obwodu RLC

L UL Uc Ug UR Ug = UL + U c + U R C R
 Drgania harmoniczne proste
Drgania harmoniczne proste Ruch harmoniczny prosty
Ruch harmoniczny prosty Ruch drgający harmoniczny wielkości charakteryzujące
Ruch drgający harmoniczny wielkości charakteryzujące Blad inklinacji
Blad inklinacji Drgania harmoniczne tłumione
Drgania harmoniczne tłumione Oscylator paul
Oscylator paul Kwantowy oscylator harmoniczny
Kwantowy oscylator harmoniczny Siatka graniastosłupa pochyłego
Siatka graniastosłupa pochyłego Ostrosłup objętość
Ostrosłup objętość Pomiary fizyczne
Pomiary fizyczne Cechy produktu turystycznego
Cechy produktu turystycznego Wyposażenie frontów przeładunkowych
Wyposażenie frontów przeładunkowych Graniastosłup pięciokątny ile ma ścian bocznych
Graniastosłup pięciokątny ile ma ścian bocznych Objętość ostrosłupa
Objętość ostrosłupa Popis prostý
Popis prostý Pozycje wyjściowe
Pozycje wyjściowe Graniastosup
Graniastosup Punkt na sferze niebieskiej
Punkt na sferze niebieskiej Ruch falowy definicja
Ruch falowy definicja Ruch laminarny
Ruch laminarny Výjezdový cestovní ruch
Výjezdový cestovní ruch Linia ktora zakresla cialo wykonujace ruch nazywamy
Linia ktora zakresla cialo wykonujace ruch nazywamy Dzial mechaniki opisujacy ruch
Dzial mechaniki opisujacy ruch Udržitelný cestovní ruch definice
Udržitelný cestovní ruch definice Model ruchu okrężnego w gospodarce otwartej
Model ruchu okrężnego w gospodarce otwartej Oprogramowanie śledzące ruch myszką
Oprogramowanie śledzące ruch myszką Przyczyny kontrreformacji
Przyczyny kontrreformacji Cestovní ruch pracovní list
Cestovní ruch pracovní list Ruch prostoliniowy wzory
Ruch prostoliniowy wzory Ruch to zdrowie prezentacja dla dzieci
Ruch to zdrowie prezentacja dla dzieci Prędkość liniowa
Prędkość liniowa Vincent ruch
Vincent ruch Ruch krzywoliniowy
Ruch krzywoliniowy Ruch jednostajnie opóźniony wzór
Ruch jednostajnie opóźniony wzór