Wykad 24 11 Ruch falowy 11 1 Fala

Wykład 24 11 Ruch falowy 11. 1 Fala jednowymiarowa 11. 2 11. 3 11. 4 11. 5 11. 6. 1 Różniczkowe równanie fali Fale harmoniczne Faza i prędkość fazowa. Zespolony zapis fali harmonicznej Rodzaje fal Fale płaskie 06 -01 -2009 Reinhard Kulessa 1

11 Ruch falowy 11. 1 Fala jednowymiarowa Pamiętamy z mechaniki, że falą nazywamy pewne zaburzenie w ośrodku sprężystym poruszające się kierunku np. x ze stałą prędkością. Zaburzenie to może zachodzić w kierunku równoległym do kierunku rozchodzenia, mamy wtedy do czynienia z falą podłużną, lub w kierunku prostopadłym do kierunku rozchodzenia, mówimy wtedy o fali poprzecznej. Prędkość rozchodzenia się fal zależy od gęstości i własności sprężystych ośrodka. Dla fali podłużnej w pręcie, E jest modułem sprężystości. 06 -01 -2009 Reinhard Kulessa 2

Dla fali poprzecznej w pręcie, jest modułem sztywności. Długość fali Najmniejszą odległość między drgającymi punktami znajdującymi się w tej samej fazie nazywamy długością fali. Miejsca geometryczne punktów do których doszło zaburzenie nazywamy czołem fali. Promień fali określa nam kierunek wzdłuż którego rozchodzi się zaburzenie. Geometryczny kształt czoła fali określa typy fal; 06 -01 -2009 Reinhard Kulessa 3

Promień fali jeśli jest to płaszczyzna, mamy falę płaską, Czoło fali jeśli jest to sfera, mamy falę kulistą Zaburzenie będzie zależało zarówno od płożenia, jak i czasu, można go zapisać jako: . 06 -01 -2009 Reinhard Kulessa 4

Dla dowolnej chwili t = const można otrzymać kształt zaburzenia. Zakładając, że mamy do czynienia z zaburzeniem nie zmieniającym kształtu wprowadzamy drugi układ współrzędnych U’ poruszający się razem z zaburzeniem z prędkością v względem układu nieruchomego U. Zobaczmy falę rozchodzącą się na linie. 06 -01 -2009 Reinhard Kulessa 5

Jaka w ogólnym przypadku będzie postać funkcji U ’ U’ vt x’=x-vt x W układzie ruchomym nie jest więcej funkcją czasu, a zależy tylko od położenia. Mamy więc: 06 -01 -2009 . Reinhard Kulessa 6

W układzie ruchomym U’ zaburzenie dla dowolnego czasu t jest takie jak w układzie nieruchomym U dla czasu t=0, w którym początki obydwu układów znajdowały się w tym samym miejscu. Współrzędne obydwu układów związane są następująco: , tak, że występujące zaburzenie można zapisać przez współrzędne układu nieruchomego U następująco: . Symbolicznie równanie fali możemy napisać następująco: . 06 -01 -2009 Reinhard Kulessa (11. 1) 7

Równaniem fali będzie również następująca funkcja. Nie przedstawia równania fali np. następujące wyrażenie: . Najbardziej znaną postacią fal są fale sinusoidalne. Równania tych fal możemy podać np. jako: . 06 -01 -2009 Reinhard Kulessa (11. 2) 8

Zależności występujące pomiędzy wielkościami charakteryzującym falę można zsumować w następującej tabelce Nazwa Długość fali Liczba falowa okres symbol k T definicja Zależności kinematyczne 2 / = k Częstość kołowa 1/T = =v. T =v prędkość v 2 = /k = v Równoważne Zapisy Równania fali 06 -01 -2009 Reinhard Kulessa 9

11. 3 Różniczkowe równanie fali wyprowadzimy w oparciu o II zasadę dynamiki Newtona zastosowaną do małego elementu drgającej struny. Poczyńmy następujące założenia: T (x, t) 1. W T x 06 -01 -2009 x+ x Napięcie T jest stałe również w czasie gdy zaburzenie przechodzi przez rozważany element strugi, 2. Zaniedbujemy ciężar W elementu struny, czyli wymagamy, że x przyczyną dynamiki jest napięcie struny, a nie grawitacja, 3. Kąt jest mały Reinhard Kulessa 10

Wielkość sił napinających jest taka sama z obu stron elementu struny, lecz przeciwnie skierowana. Tp(x+ x) T T Tp(x) x x+ x x Wypadkowa pionowa siła napinająca strunę Tp(x+ x)-Tp(x) nadaje segmentowi pionowe przyśpieszenie zgodnie z II zasada dynamiki Newtona. Jeżeli struna ma masę M i długość L, to masa struny na jednostkę długości wynosi M/L. Rozważany segment ma więc masę M/L · x. 06 -01 -2009 Reinhard Kulessa 11

Pionowe przyśpieszenie uzyskane przez strunę oznaczamy jako; . Drugie prawo Newtona zapisujemy w postaci: . Zmniejszając przedział x do zera możemy napisać; . Zakładając, że kąt jest mały możemy napisać; . 06 -01 -2009 Reinhard Kulessa 12

Doprowadzamy więc nasze równanie do następującej postaci; . Wyrażenie T L/M ma wymiar kwadratu prędkości. Na początku tego rozdziału podaliśmy wyrażenia na prędkości fal poprzecznych i podłużnych. T L/M możemy przekształcić do postaci: , gdzie jest naciągiem struny, a gęstością materiału struny. 06 -01 -2009 Reinhard Kulessa 13

Różniczkowe równanie fali ma więc postać: . (11. 3) Jako ciekawostkę omówmy dwa przypadki fal na wodzie. 1. Głębokość h << -czyli płytka woda, wtedy 2. Głębokość h >> -czyli głęboka woda, wtedy , gdzie jest napięciem powierzchniowym wody. 06 -01 -2009 Reinhard Kulessa 14

Dla prędkości fal na głębokiej wodzie istnieje minimalna prędkość. Można ją znaleźć z podanego wzoru. . Podstawiając równanie na długość fali do odpowiedniego wzoru na prędkość, otrzymujemy; . 06 -01 -2009 Reinhard Kulessa 15

11. 2 Fale harmoniczne Do tej pory nadaliśmy funkcji falowej (x; t) jedynie postać funkcji sinusoidalnych. Funkcja, która będzie rozwiązaniem różniczkowego równania fali będzie miała postać: , gdzie k jest stałą dodatnią. Ustalenie położenia lub czasu prowadzi do sinusoidalnego zaburzenia . Fala jest periodyczna zarówno w przestrzeni jak i w czasie. Odległość po której powtarza się (okres) zaburzenie przestrzenne nazywamy jak już powiedzieliśmy długością fali i oznaczamy przez . Zmiana położenia o długość fali nie zmienia zaburzenia . Mamy więc: . 06 -01 -2009 Reinhard Kulessa 16

W rozważanym przypadku oznacza to zmianę argumentu funkcji sinus o ± 2. Mamy więc: . Wynika stąd, że , oraz , gdyż zarówno k jak i są dodatnie. W sposób analogiczny możemy zbadać periodyczność funkcji ze względu na czas, czyli wyznaczyć okres fali T. Jest to czas, w którym fala o długości przebiega obok nieruchomego obserwatora. Ponieważ chodzi nam o zależność czasową, możemy napisać: 06 -01 -2009 Reinhard Kulessa 17

, czyli, Wynika stąd, że . . Wiedząc, że wszystkie powyższe wielkości są dodatnie, otrzymujemy. Odwrotnością okresu T jest jak wiadomo częstość ; Dla fali definiujemy jeszcze częstość kątową i częstość przestrzenną . Przy czym, 06 -01 -2009 Reinhard Kulessa 18

Zdefiniowane wielkości charakteryzujące fale harmoniczne dotyczą również fal nieharmonicznych, jak długo przedstawiają one pewne periodyczne zaburzenia. 11. 3 Faza i prędkość fazowa. Rozpatrzmy dowolną funkcję harmoniczną: Cały argument funkcji sinus nazywamy fazą (kątem fazowym ) , tak, że. 06 -01 -2009 Reinhard Kulessa 19

W tym zapisie dla kąta fazowego = 0 ( czyli dla t=0, x=0) wartość zaburzenia jest też równa zero. Tak nie zawsze musi być, dlatego wprowadza się fazę początkową tak, że ogólna postać równania przyjmuje postać: . Faza (kąt fazowy) powyższego zaburzenia można podać w następującej postaci: . Faza ta jest funkcją położenia i czasu. Zmianę fazy w czasie przy stałym położeniu definiuje prędkość kątową . . 06 -01 -2009 Reinhard Kulessa 20

Z kolei zmiana fazy w funkcji położenia dla ustalonego czasu prowadzi do równania; . W oparciu o własności pochodnych cząstkowych możemy napisać; Lewa strona tego równania przedstawia prędkość rozprzestrzeniania się zaburzenia dla stałej fazy. Uwzględniając poprzednie równania otrzymujemy; 06 -01 -2009 Reinhard Kulessa 21

Powyższy wzór definiuje prędkość z którą porusza się zaburzenie. Jest to tzw. prędkość fazowa. 11. 4 Zespolony zapis fali harmonicznej Falę harmoniczną możemy napisać w postaci: , czyli, 11. 5 . Rodzaje fal Zapoznajmy się z różnymi rodzajami fal z którymi możemy mieć do czynienia. Ze względu na kierunek rozchodzenia się zaburzenia w stosunku do kierunku rozchodzenia się fali możemy mieć fale poprzeczne i podłużne. 06 -01 -2009 Reinhard Kulessa 22

Ze względu na kształt czoła fali możemy mieć fale płaskie i kuliste. Ze względu na charakter zaburzenia fale mogą być skalarne (np. fala dźwiękowa w powietrzu) lub wektorowe (np. fala świetlna). Możemy mieć również fale spolaryzowane (zaburzenie zachowuje stały kierunek) Omówmy dokładniej fale płaskie i kuliste. 11. 5. 1 Fale płaskie Oczywistym jest, że fale rozchodzą się w przestrzeni we wszystkich trzech kierunkach. Fala płaska jest najprostszym przykładem fali trójwymiarowej. Miejsce geometryczne punktów o tej samej fazie tworzy płaszczyznę. Płaszczyzny 06 -01 -2009 Reinhard Kulessa 23

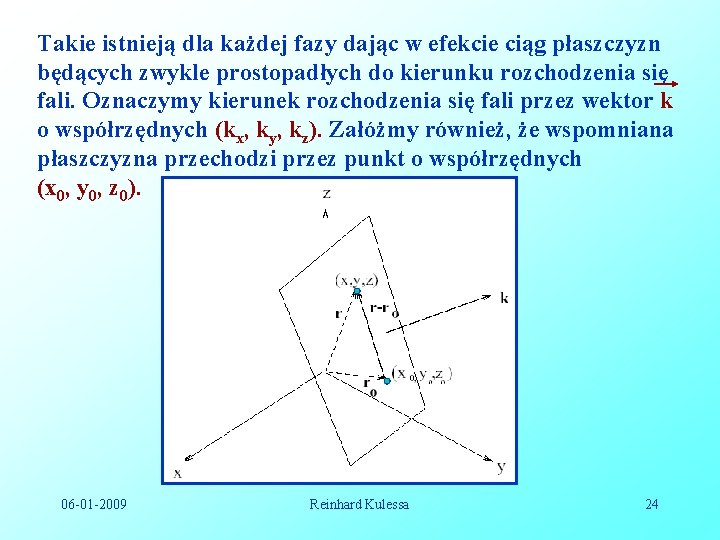
Takie istnieją dla każdej fazy dając w efekcie ciąg płaszczyzn będących zwykle prostopadłych do kierunku rozchodzenia się fali. Oznaczymy kierunek rozchodzenia się fali przez wektor k o współrzędnych (kx, ky, kz). Załóżmy również, że wspomniana płaszczyzna przechodzi przez punkt o współrzędnych (x 0, y 0, z 0). 06 -01 -2009 Reinhard Kulessa 24

Jeśli wektor wodzący r określa dowolny punkt w przestrzeni, to wyrażenie; umieszcza wektor r – r 0 na płaszczyźnie prostopadłej do wektora k, przy czym współrzędne końca wektora r – r 0 ; (x, y, z) przyjmują wszystkie dozwolone wartości. Przyjmując, że k (kx, ky, kz) otrzymujemy w oparciu o poprzednie równanie; , lub . Wyrażenie 06 -01 -2009 Reinhard Kulessa 25

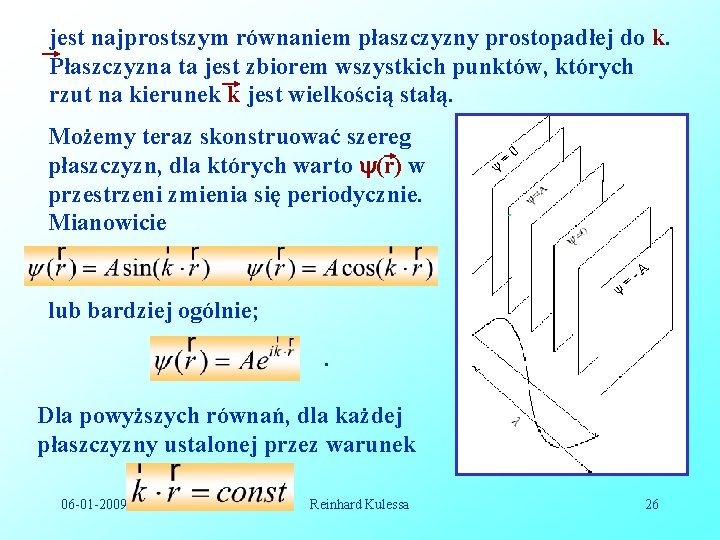
jest najprostszym równaniem płaszczyzny prostopadłej do k. Płaszczyzna ta jest zbiorem wszystkich punktów, których rzut na kierunek k jest wielkością stałą. Możemy teraz skonstruować szereg płaszczyzn, dla których warto (r) w przestrzeni zmienia się periodycznie. Mianowicie = 0 lub bardziej ogólnie; = -A . Dla powyższych równań, dla każdej płaszczyzny ustalonej przez warunek 06 -01 -2009 Reinhard Kulessa 26

(r) przyjmuje wartość stałą. Dla fal harmonicznych wartości powinny powtórzyć się w przestrzeni po przesunięciu o w kierunku k. Przedstawia to ostatni rysunek. Rysunek poprzedni przedstawia tylko niektóre z nieskończonej liczby płaszczyzn. Przestrzenną powtarzalność harmonicznego zaburzenia, możemy przedstawić następująco; , Gdzie ko jest wektorem jednostkowym w kierunku wektora falowego. W układzie kartezjańskim płaska fala harmoniczna ma następująca postać; . 06 -01 -2009 Reinhard Kulessa 27

lub. 06 -01 -2009 Reinhard Kulessa 28