Valutazione delle ipotesi Valutazione empirica delle ipotesi Dato

Valutazione delle ipotesi

Valutazione empirica delle ipotesi • Dato un valore di accuratezza di classificazione misurato su un campione, quanto questo valore è accurato nella stima di ulteriori campioni? • Se una ipotesi h risulta prevalere su un’ipotesi h’ su un campione di test, possiamo dire che h “è meglio” di h’ in generale? • Quando il campione di dati annotati (D) è limitato, quale è il metodo migliore per utilizzarlo sia in fase di apprendimento che di test?

Definizioni di errore • Sia T un insieme di tuple <x, c(x)> in generale, T D • Errore sul campione (sample error) n è il numero di tuple in T e la funzione è 1 se c(x)=h(x), 0 altrimenti • Errore reale dove D è la distribuzione di probabilità delle istanze • Quindi, e. T è una stima, e siamo interessati a scoprire quanto questa stima si discosti dalla “realtà”, rappresentata da e. D

Intervalli di confidenza • Ci interessa valutare i margini di discrepanza fra errore reale ed errore stimato. • Vogliamo stimare la probabilità che dove UB e LB sono dei valori di discrepanza massimo e minimo (upper bound e lower bound) • UB e LB definiscono un intervallo di confidenza • Def: un intervallo di confidenza del N% per un parametro p è un intervallo [LB, UB]che include p con probabilità N% (ovvero: con probabilità N% si ha che LB p UB)

Altre definizioni (reminder) • Distribuzione di probabilità per una variabile aleatoria Y specifica la probabilità Pr(Y=yi) yi • Densità di probabilità (nel continuo) • Valore atteso o media, a volte indicato anche con Y • Varianza caratterizza la dispersione della distribuzione attorno alla media • Deviazione standard

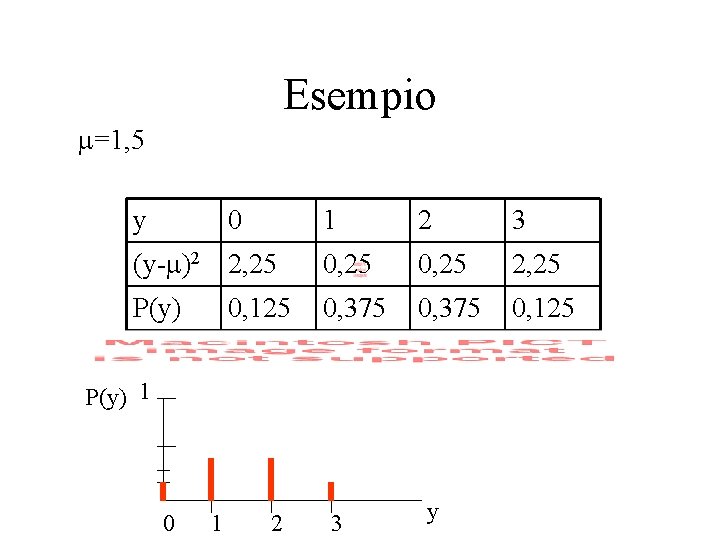
Esempio =1, 5 y 0 1 2 3 (y- )2 2, 25 0, 25 2, 25 P(y) 0, 375 0, 125 P(y) 1 0 1 2 3 y

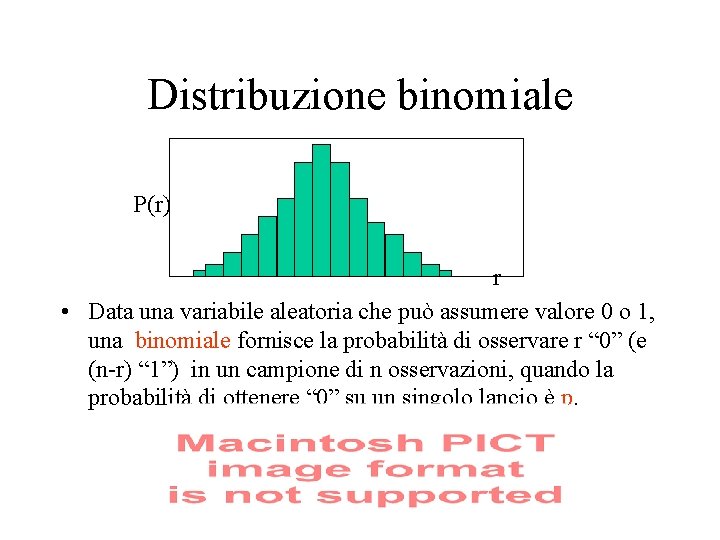
Distribuzione binomiale P(r) r • Data una variabile aleatoria che può assumere valore 0 o 1, una binomiale fornisce la probabilità di osservare r “ 0” (e (n-r) “ 1”) in un campione di n osservazioni, quando la probabilità di ottenere “ 0” su un singolo lancio è p.

Stima dell’errore • La stima dell’errore e. D(h) sulla base di un insieme casuale di osservazioni indipendenti equivale alla stima del parametro p della binomiale. Il numero r rappresenta il numero di errori osservabili in n classificazioni di istanze x nel test set T. • e. D(h) =p • e. T(h) è detto uno stimatore di p • Il pregiudizio, o bias, della stima è definito dalla E[e. T(h)]-p • Una stima si dirà unbiased se il valore medio di molte stime di e. T(h) (la variabile aleatoria) converge verso p r segue una binomiale

Torniamo al problema degli intervalli di confidenza • un intervallo di confidenza del N% per un parametro p è un intervallo [LB, UB]che include p con probabilità N% • È complicato stimare questi intervalli per una distribuzione binomiale • Viceversa, e molto più facile farlo per una distribuzione Normale o Gaussiana

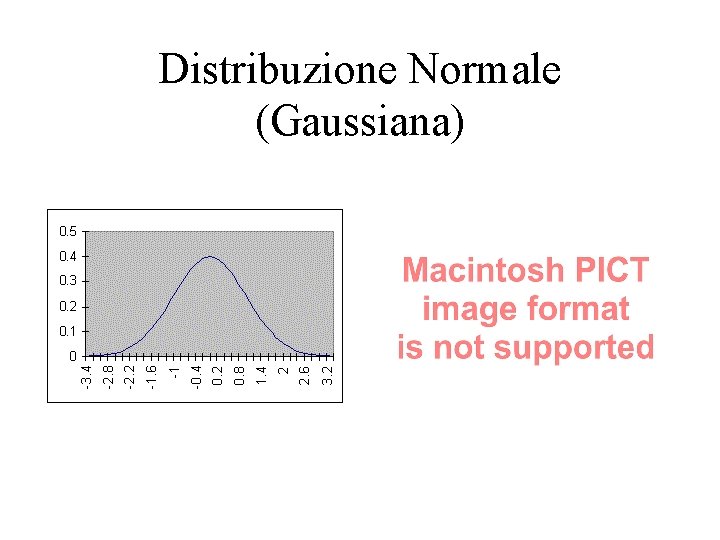
Distribuzione Normale (Gaussiana)

Intervalli di confidenza in una distribuzione normale o Gaussiana • Se una variabile aleatoria X obbedisce ad una distribuzione Normale con media e deviazione standard , allora una misura x della variabile X cadrà nell’intervallo N% delle volte • Equivalentemente, avrò per la stima di il seguente intervallo:

Teorema del Limite Centrale • La distribuzione Normale o Gaussiana è interessante perché consente di calcolare in modo semplice degli intervalli di confidenza (integrale) • Il Teorema del Limite Centrale stabilisce che la somma di un numero sufficientemente grande di variabili aleatorie indipendentemente distribuite segue una distribuzione che è approssimativamente normale • La distribuzione che governa tende alla distribuzione Normale per n • In pratica, questo è approssimativamente vero per n>30

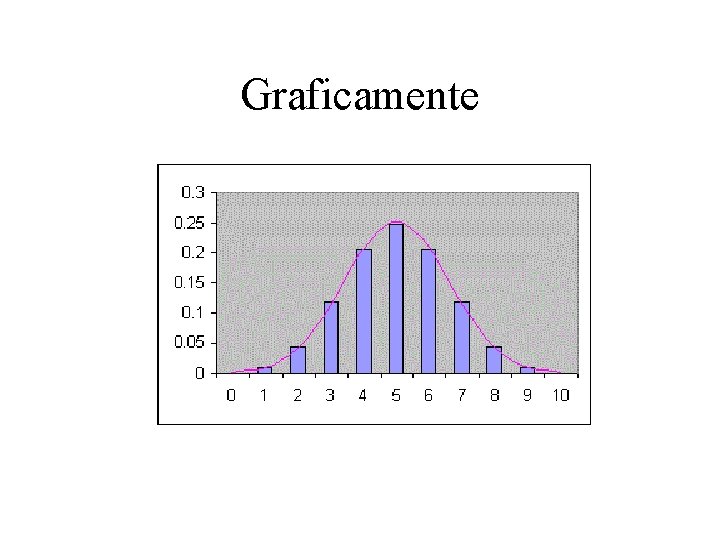
Graficamente

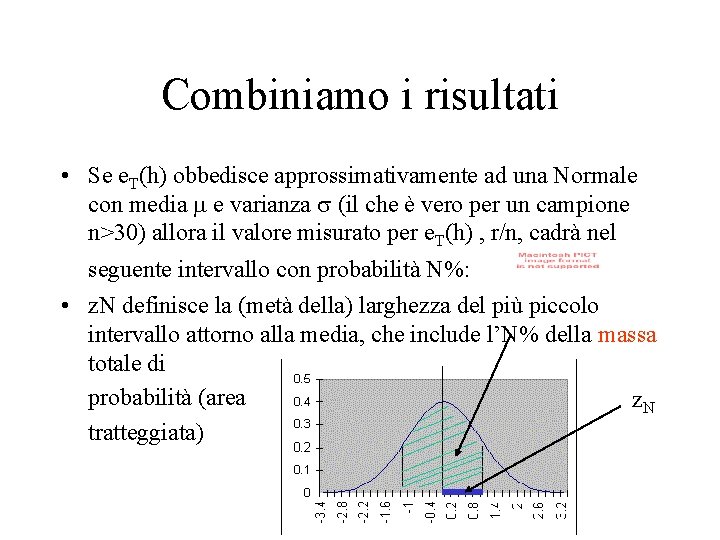
Combiniamo i risultati • Se e. T(h) obbedisce approssimativamente ad una Normale con media e varianza (il che è vero per un campione n>30) allora il valore misurato per e. T(h) , r/n, cadrà nel seguente intervallo con probabilità N%: • z. N definisce la (metà della) larghezza del più piccolo intervallo attorno alla media, che include l’N% della massa totale di probabilità (area z. N tratteggiata)

Determiniamo l’intervallo • N% dell’area giace in z. N • 80% dell’area giace in 1, 28 • Per una Normale con media 0 e deviazione standard 1: • Ricordando che: • Otteniamo:

Migliorare la stima dell’errore mediante stime multiple

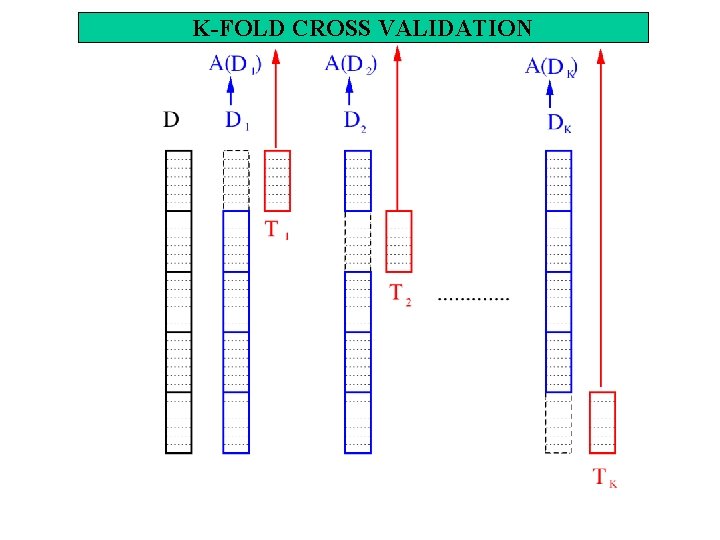
K-fold cross validation • Suddividere i dati di apprendimento D in k sotto-insiemi di uguale taglia D 1, D 2, . . Dk • Per i=1. . K do: – Li (D-Di), Ti Di (usa Di come test set e tutto il resto come learning set) – Calcola l’errore medio: – Intervallo di confidenza N%: – k-1 (indicato spesso con n) indica il numero di gradi di libertà (numero degli eventi indipendenti che concorrono nella produzione del valore della variabile aleatoria ).

K-FOLD CROSS VALIDATION

Verificare ipotesi alternative • Date due ipotesi h 1 e h 2, la differenza è: perché la varianza di questa distribuzione è pari alla somma delle varianze delle due distribuzioni • L’intervallo di confidenza all’N% sarà:

Verificare algoritmi alternativi • Ad esempio, due architetture G e G’ di rete neurale, o due algoritmi di alberi di decisione, basati su diverse politiche • Siano LA e LB due apprendisti: – Suddividere i dati di apprendimento D in k sotto-insiemi di uguale taglia D 1, D 2, . . Dk – Per i=1. . K do: – Li (D-Di), Ti Di (usa Di come test set e tutto il resto come learning set) – h. A=LA(Li), h. B=LB(Li) – i=e. Ti(h. A)- e. Ti(h. B) • Intervallo di confidenza N%: