Understanding Parallel Repetition Requires Understanding Foams Uri Feige

Understanding Parallel Repetition Requires Understanding Foams Uri Feige Guy Kindler Ryan O’Donnell Microsoft Weizmann CMU

What we wanted to solve Strong Parallel Repetition Problem: Let G be a 2 -prover 1 -round game with answer sets A, B. val( G ) · 1 − Is it true that ) val( G d ) · (1 − ( ))d/log(|A||B|) ?

A special case Strong Unique-Games Parallel Repetition Problem: Let G be a 2 P 1 R game with answer sets A, B and unique constraints. val( G ) · 1 − Is it true that ) val( G d ) · (1 − ( ))d/log(|A||B|) ?

A further special case Strong 2 -Lin Parallel Repetition Problem: Let G be a 2 P 1 R game with 2 -Lin constraints. val( G ) · 1 − Is it true that ) val( G d ) · (1 − ( ))d ?

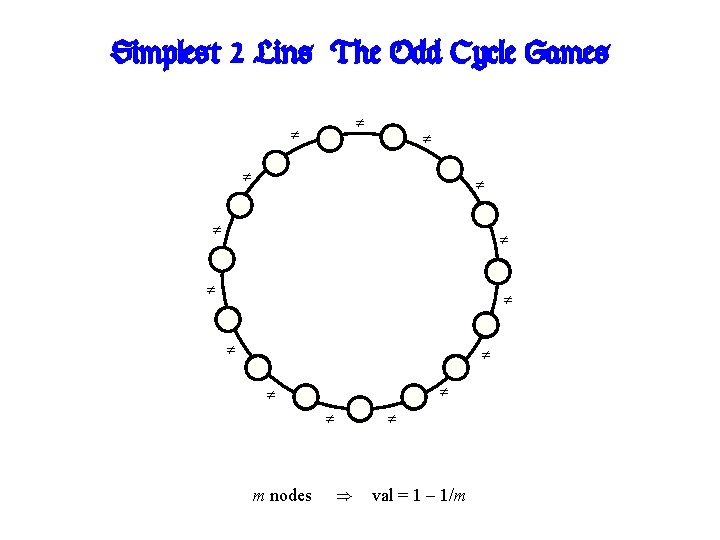
A further special case Odd-Cycle Parallel Repetition Problem: Let GCm be the Odd-Cycle game of length m, which satisfies Is it true that val(GCm ) = 1 − (1/m). val(GCm d ) · (1 − (1/m))d ?

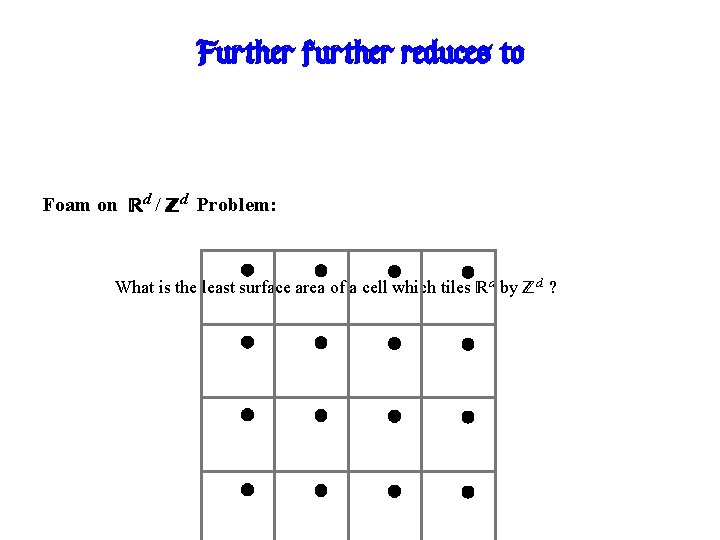
Further reduces to Torus Blocking Problem on (Zmd)1: Let (Zmd)1 be the “discrete torus graph”: vertex set = Zmd, edge set = {(x, y) : ||x − y||1 · 1}. To block all cycles that “wrap around”, what’s the least fraction of edges you can delete?

Our results • Improved lower bound for Torus Blocking Problem, which implies • Improved upper bounds for Odd Cycle Parallel Repetition problem. • At least, if you look at the parameters in the right way.

This looks kind of pathetic

But it’s not our fault

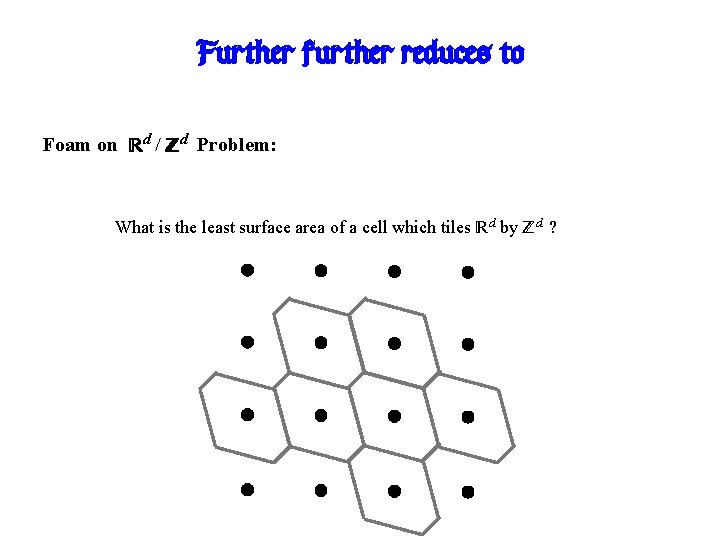
Further further reduces to Foam on Rd / Zd Problem: What is the least surface area of a cell which tiles Rd by Zd ?

Further further reduces to Foam on Rd / Zd Problem: What is the least surface area of a cell which tiles Rd by Zd ?

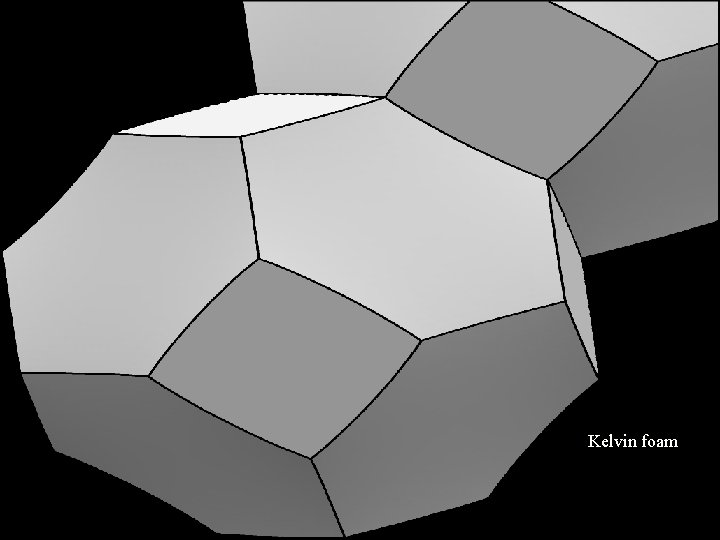
Kelvin foam

Similar questions are hard open problems in geometry

Foam on Rd / Zd Let A(d) denote the least possible surface area… ÷ 2. Upper bound? A(d ) · d. the unit cube Lower bound? the volume-1 ball

Other bounds • • • A(d) · d − 2−O(d log d) (put a radius-½ sphere at cube’s corner) (the hexagon was optimal [Choe’ 89]) For d = 3, nothing known except sphere vs. cube: 2. 42 ¼ (9 /2)1/3 · A(3) < 3. Experts’ d = 3 conjecture: same combinatorial structure as “Kelvin Foam”

A prize For £ 100: Prove or disprove: For £ 25: Prove A(d) ¸ d 1−o(1).

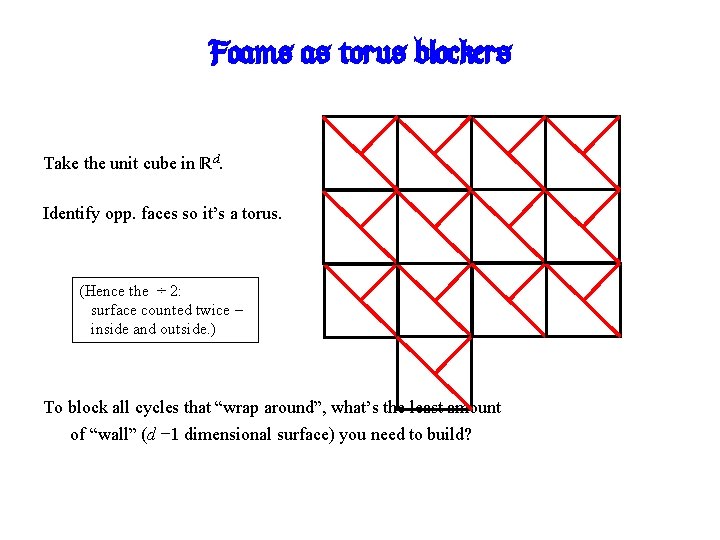
Foams as torus blockers Take the unit cube in Rd. Identify opp. faces so it’s a torus.

Foams as torus blockers Take the unit cube in Rd. Identify opp. faces so it’s a torus.

Foams as torus blockers Take the unit cube in Rd. Identify opp. faces so it’s a torus.

Foams as torus blockers Take the unit cube in Rd. Identify opp. faces so it’s a torus. To block all cycles that “wrap around”, what’s the least amount of “wall” (d − 1 dimensional surface) you need to build?

Foams as torus blockers Take the unit cube in Rd. Identify opp. faces so it’s a torus. (Hence the ÷ 2: surface counted twice – inside and outside. ) To block all cycles that “wrap around”, what’s the least amount of “wall” (d − 1 dimensional surface) you need to build?

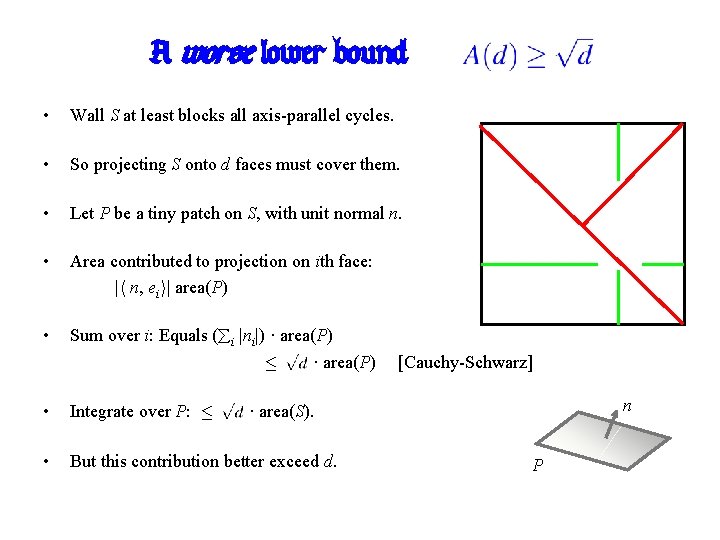
A worse lower bound: • Wall S at least blocks all axis-parallel cycles. • So projecting S onto d faces must cover them. • Let P be a tiny patch on S, with unit normal n. • Area contributed to projection on ith face: |h n, eii| area(P) • Sum over i: Equals ( i |ni|) · area(P) · · area(P) • Integrate over P: · • But this contribution better exceed d. ssss [Cauchy-Schwarz] n · area(S). P

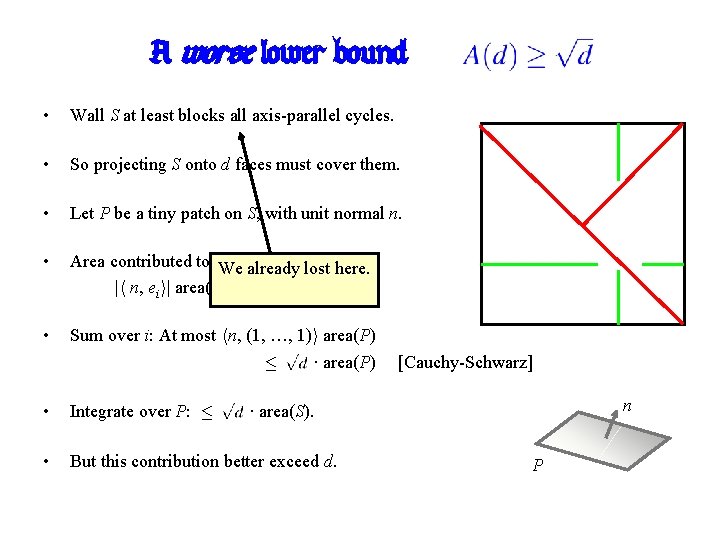
A worse lower bound: • Wall S at least blocks all axis-parallel cycles. • So projecting S onto d faces must cover them. • Let P be a tiny patch on S, with unit normal n. • Area contributed to projection ith here. face: We alreadyonlost |h n, eii| area(P) • Sum over i: At most hn, (1, …, 1)i area(P) · · area(P) • Integrate over P: · • But this contribution better exceed d. ssss [Cauchy-Schwarz] n · area(S). P

What’s this got to do with Parallel Repetitio What is Parallel Repetition?

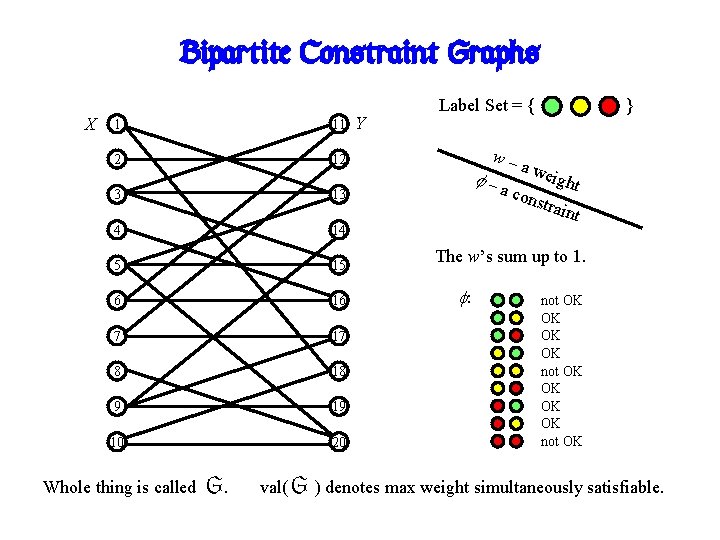
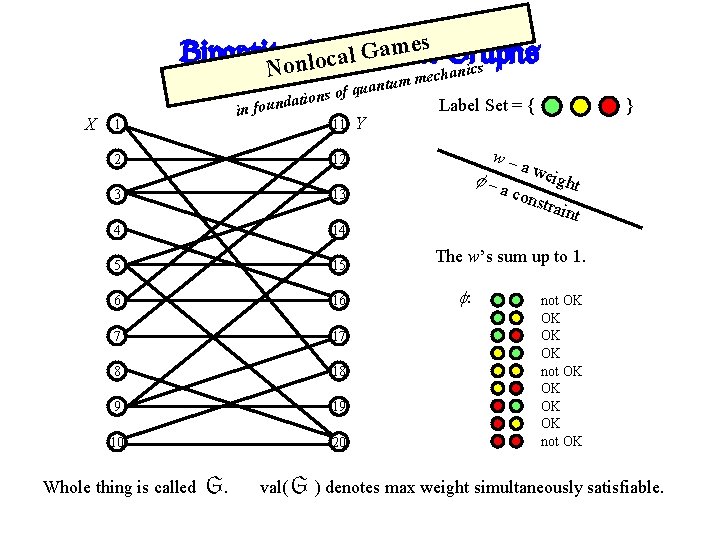
Bipartite Constraint Graphs X 1 11 2 12 3 13 4 14 5 15 6 16 7 17 8 18 9 19 10 20 Whole thing is called G. Y Label Set = { w– –a } a we ight cons train t The w’s sum up to 1. : not OK OK not OK val( G ) denotes max weight simultaneously satisfiable.

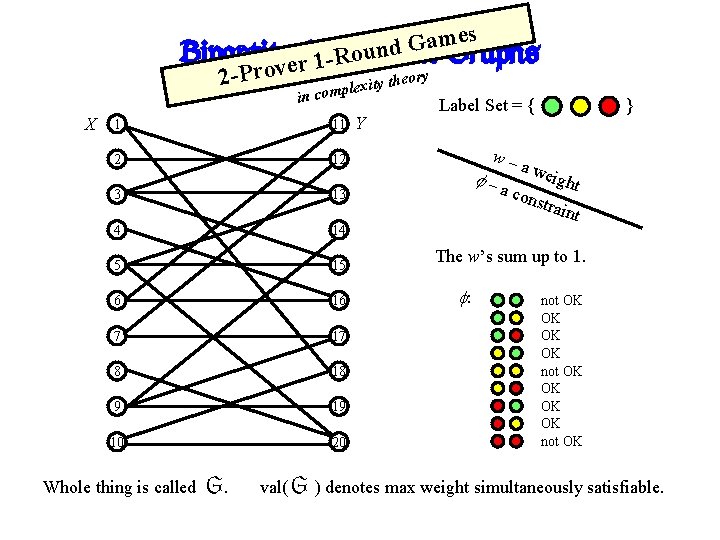
es m a G d un o Bipartite Constraint Graphs R 1 r e v 2 -Pro y theory t i x e l p m in co X 1 11 2 12 3 13 4 14 5 15 6 16 7 17 8 18 9 19 10 20 Whole thing is called G. Y Label Set = { w– –a } a we ight cons train t The w’s sum up to 1. : not OK OK not OK val( G ) denotes max weight simultaneously satisfiable.

es Graphs m a G Bipartite Constraint l a Nonloc anics mech m u t n s of qua n o i t a d un X in fo 1 11 2 12 3 13 4 14 5 15 6 16 7 17 8 18 9 19 10 20 Whole thing is called G. Y Label Set = { w– –a } a we ight cons train t The w’s sum up to 1. : not OK OK not OK val( G ) denotes max weight simultaneously satisfiable.

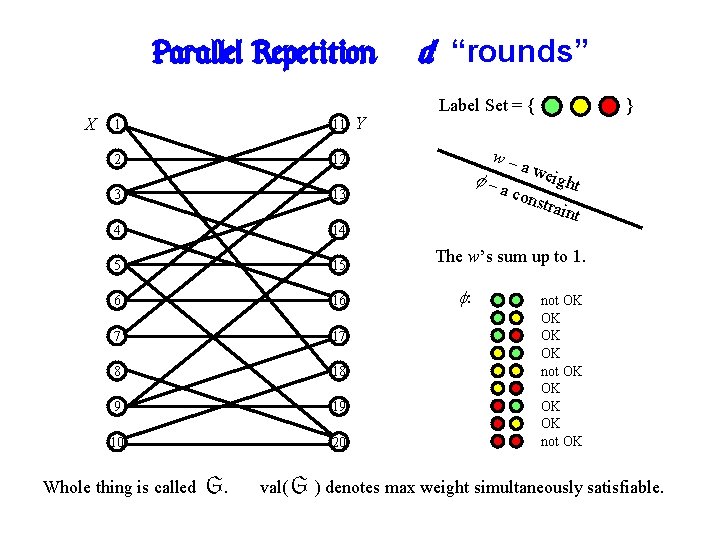
Parallel Repetition: X 1 11 2 12 3 13 4 14 5 15 6 16 7 17 8 18 9 19 10 20 Whole thing is called G. Y d “rounds” Label Set = { w– –a } a we ight cons train t The w’s sum up to 1. : not OK OK not OK val( G ) denotes max weight simultaneously satisfiable.

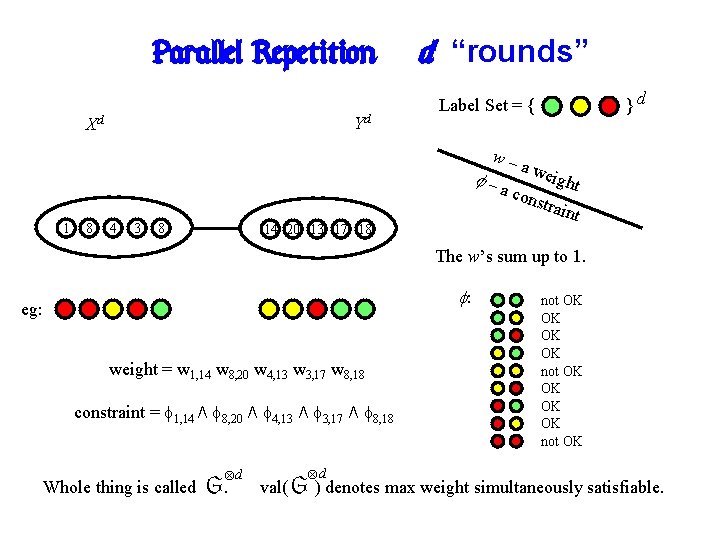
Parallel Repetition: Yd Xd d “rounds” w– –a 1 8 4 3 8 }d Label Set = { 14 20 13 17 18 a we ight cons train t The w’s sum up to 1. : eg: weight = w 1, 14 w 8, 20 w 4, 13 w 3, 17 w 8, 18 constraint = 1, 14 8, 20 4, 13 3, 17 8, 18 Whole thing is called d G. d not OK OK not OK val( G ) denotes max weight simultaneously satisfiable.

Value under Parallel Repetition True or False? val(G d) = val(G)d ? false val(G d) · val(G) ? true val(G 2) < val(G) ? false val(G d) ! 0 as d ! 1 ? true (took 6 years to prove)

Raz’s Parallel Repetition Theorem Raz ’ 95: val( G ) · 1 − ) val( G d ) · (1 − poly( )) d/log(# labels) Tremendously important theorem for proving hardness of approximation results. Holenstein ’ 07: poly( ) can be 3 / 4000. Strong Parallel Repetition Problem: can this be improved to ( )?

The “ 2 -Lin” special case # labels = 2, each constraint is either “=” or “ ” Feige-Lovász ’ 91 + Goemans-Williamson ’ 95: val( G ) · 1 − ) val( G d ) · (1 − c 2)) d, 2 where c = /4. Strong 2 -Lin Parallel Repetition Problem: Can this be improved to ( )? My conjecture: Yes. My motivation: Would show that sharp hardness-of-approx for Max-Cut is “Unique Games Conjecture”-complete, not just “Unique Games Conjecture”-hard.

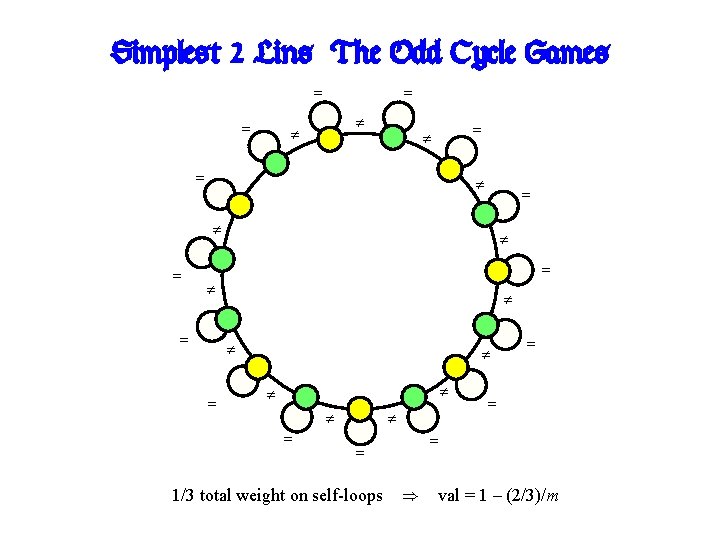
Simplest 2 -Lins: The Odd Cycle Games m nodes ) val = 1 – 1/m

Simplest 2 -Lins: The Odd Cycle Games = = = = = = = 1/3 total weight on self-loops = ) val = 1 – (2/3)/m

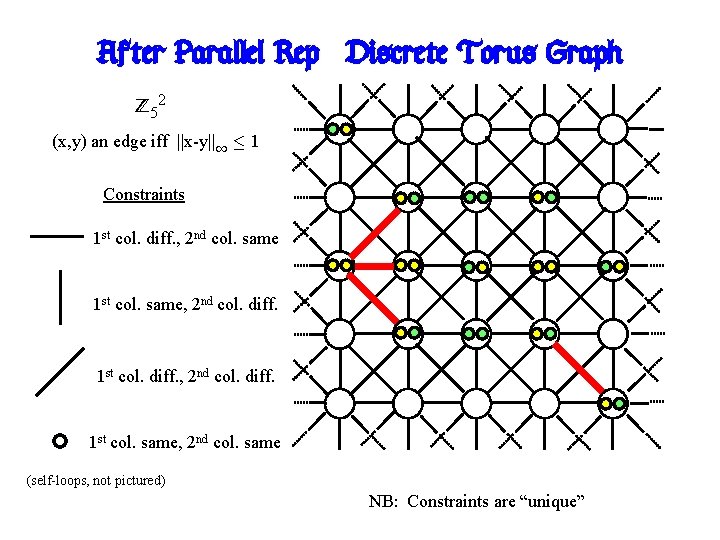
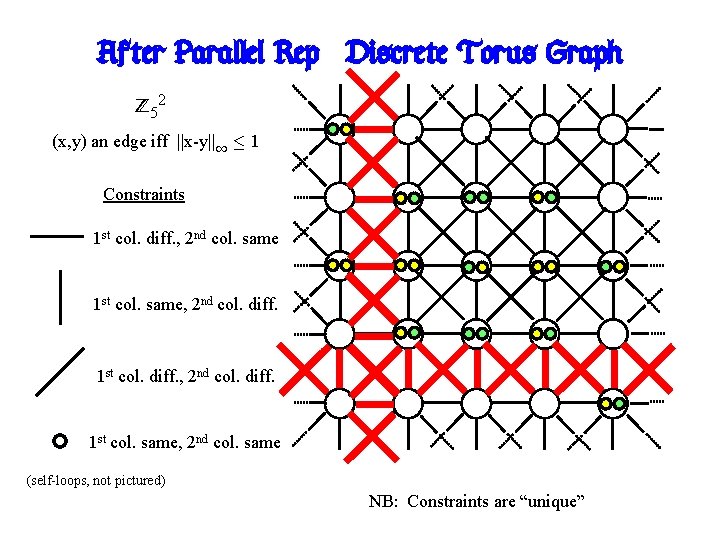
After Parallel Rep: Discrete Torus Graph Z 52 (x, y) an edge iff ||x-y||1 · 1 Constraints 1 st col. diff. , 2 nd col. same 1 st col. same, 2 nd col. diff. 1 st col. diff. , 2 nd col. diff. 1 st col. same, 2 nd col. same (self-loops, not pictured) NB: Constraints are “unique”

After Parallel Rep: Discrete Torus Graph Z 52 (x, y) an edge iff ||x-y||1 · 1 Constraints 1 st col. diff. , 2 nd col. same 1 st col. same, 2 nd col. diff. 1 st col. diff. , 2 nd col. diff. 1 st col. same, 2 nd col. same (self-loops, not pictured) NB: Constraints are “unique”

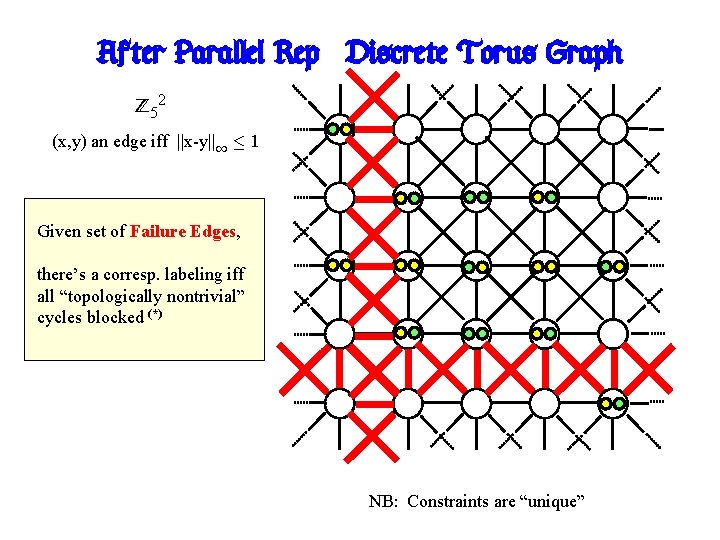
After Parallel Rep: Discrete Torus Graph Z 52 (x, y) an edge iff ||x-y||1 · 1 Given set of Failure Edges, there’s a corresp. labeling iff all “topologically nontrivial” cycles blocked (*) NB: Constraints are “unique”

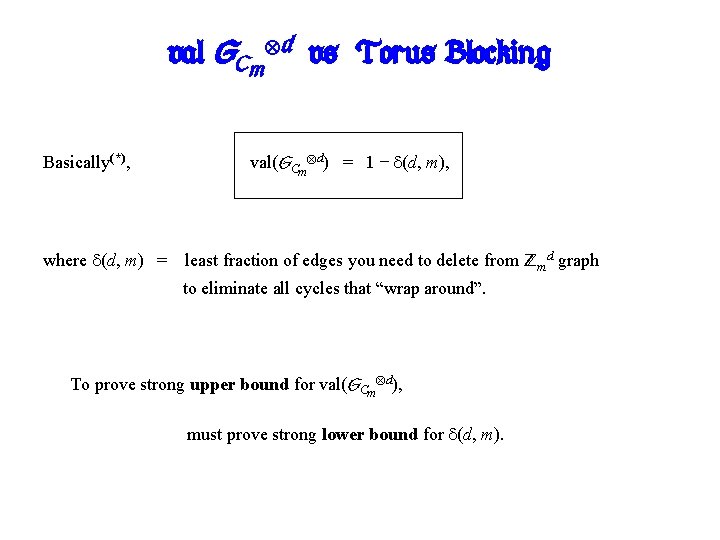
val(GCm d) vs. Torus Blocking Basically(*), val(GCm d) = 1 − (d, m), where (d, m) = least fraction of edges you need to delete from Zmd graph to eliminate all cycles that “wrap around”. To prove strong upper bound for val(GCm d), must prove strong lower bound for (d, m).

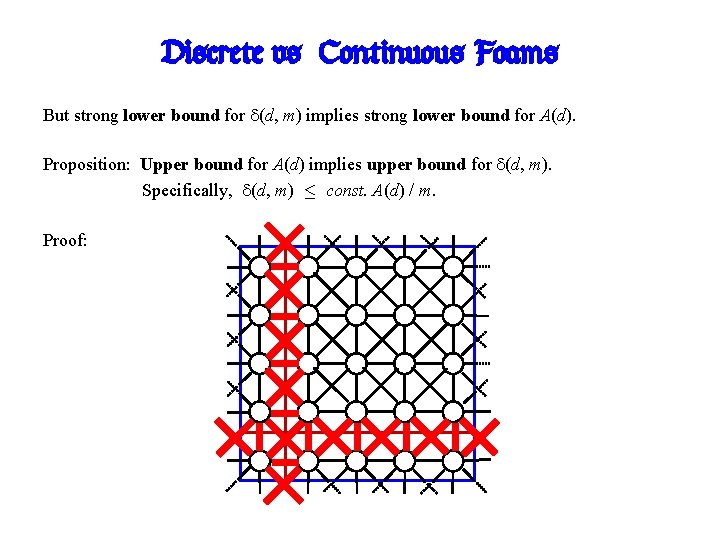
Discrete vs. Continuous Foams But strong lower bound for (d, m) implies strong lower bound for A(d). Proposition: Upper bound for A(d) implies upper bound for (d, m). Specifically, (d, m) · const. A(d) / m. Proof:

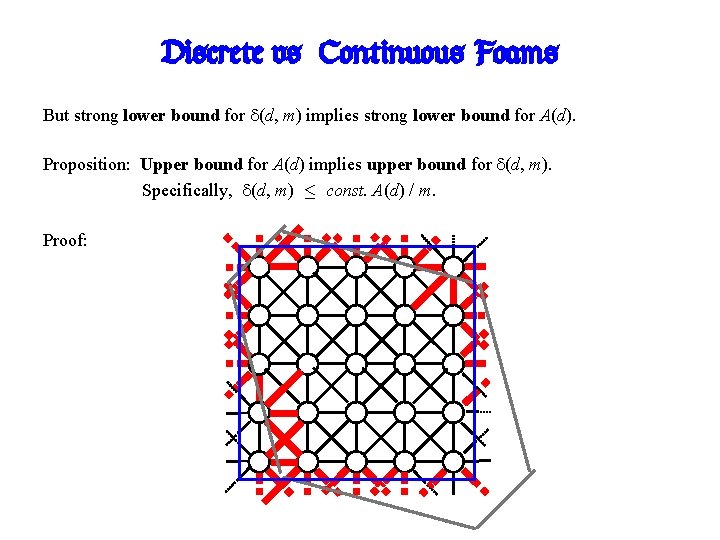
Discrete vs. Continuous Foams But strong lower bound for (d, m) implies strong lower bound for A(d). Proposition: Upper bound for A(d) implies upper bound for (d, m). Specifically, (d, m) · const. A(d) / m. Proof:

Hence the paper’s title To understand the truth about parallel repetition, you must get good upper bounds for val(GCm d) (a special case of the general case). But this requires good lower bounds for the continuous Rd / Zd Foam Problem.

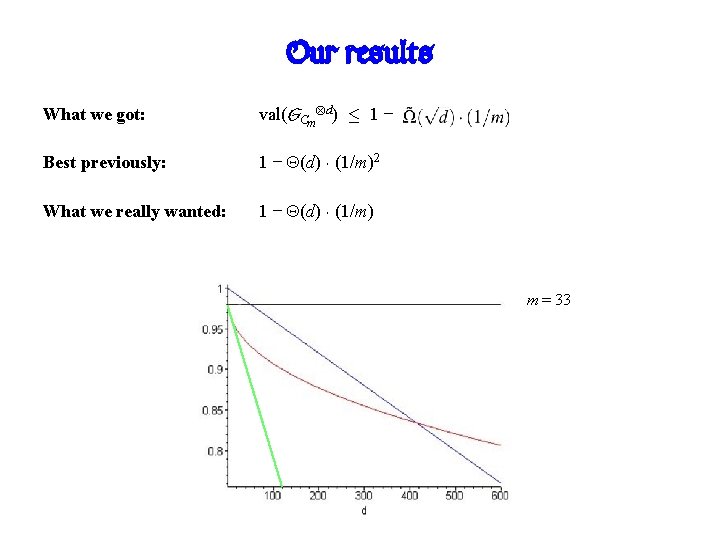
Our results What do we actually prove in the paper? ! Main Theorem: The continuous foam lower bound can be discretified into a lower bound for (d, m): (d, m) ¸ Hence val(GCm d) · 1 − Proof: A lot of Fourier analysis. (if d · m 2 log m, say).

Our results What we got: val(GCm d) · 1 − Best previously: 1 − (d) ¢ (1/m)2 What we really wanted: 1 − (d) ¢ (1/m) m = 33