Una proposicin es un enunciado u oracin declarativa



































- Slides: 55

Una proposición es un enunciado u oración declarativa de la cual se puede afirmar que es falsa o verdadera pero no ambas cosas a la vez Ejemplos: ¿ Son los siguientes enunciados proposiciones? . 1. 2. 3. 4. 5. 6. 7. 8. La tierra es cuadrada. ¿Habla usted francés? . ¿Qué hora es? . Buenas tardes 1+1=3. !Ayúdeme por favor!. 7 es mayor que 9. Luisa estudia medicina.

Los conectivos lógicos son las palabras como y, o, no, si…entonces, que permiten combinar proposiciones simples para producir otras, llamadas proposiciones compuestas. Sus símbolos son: ~ negación conjunción disyunción exclusiva condicional bicondicional

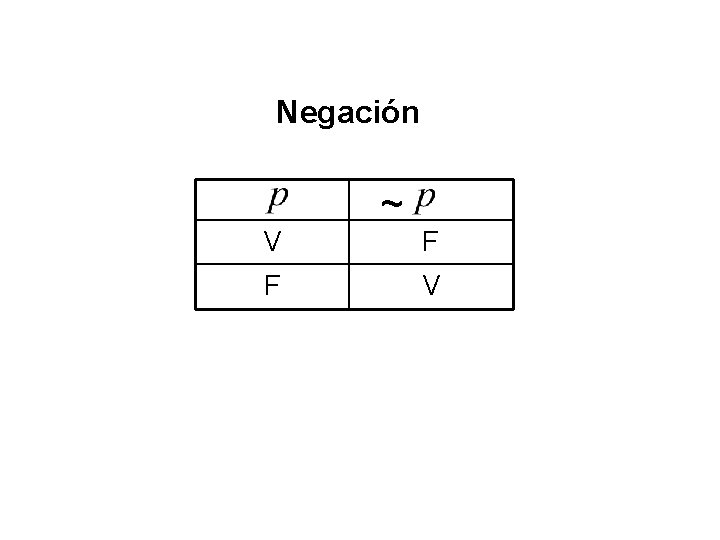
Negación ~ V F F V

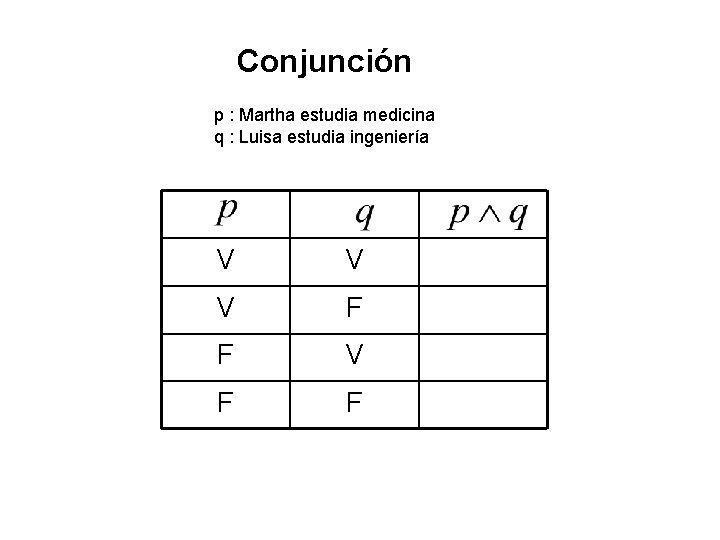
Conjunción p : Martha estudia medicina q : Luisa estudia ingeniería V V V F F

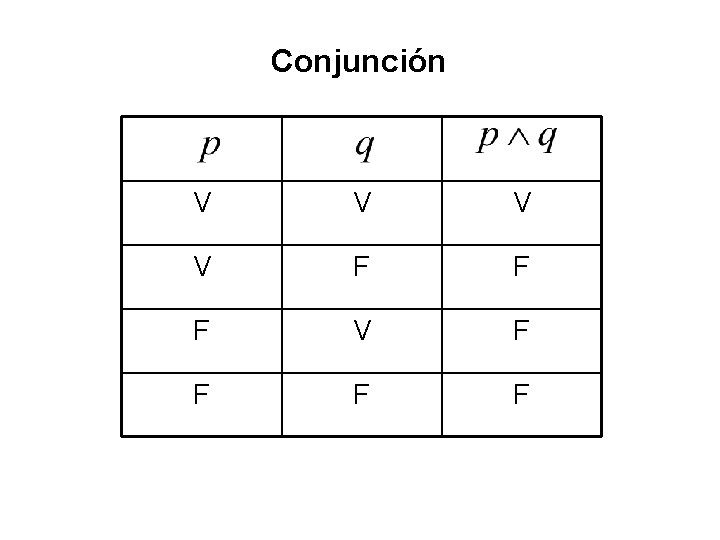
Conjunción V V F F F V F F

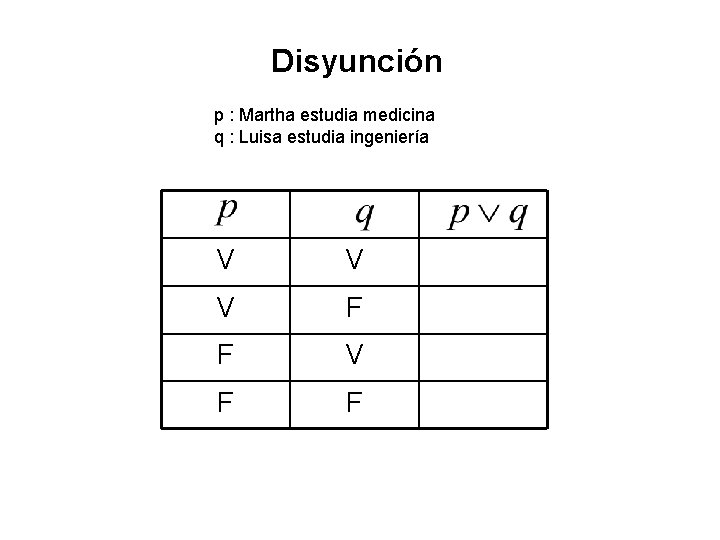
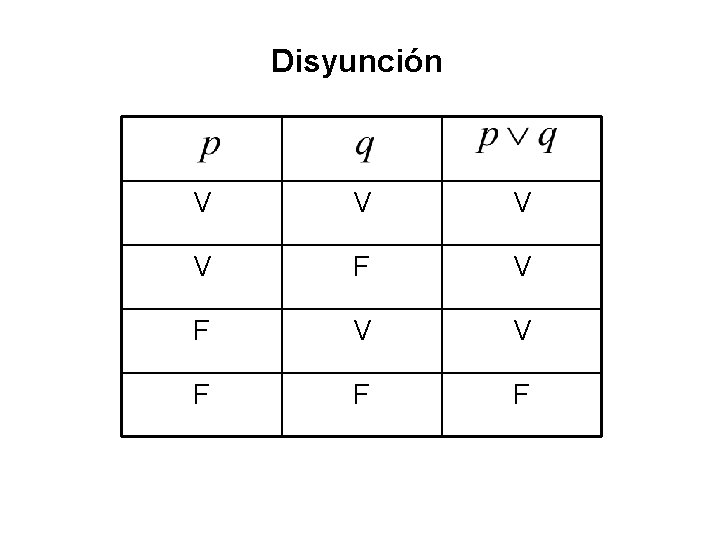
Disyunción p : Martha estudia medicina q : Luisa estudia ingeniería V V V F F

Disyunción V V F F F

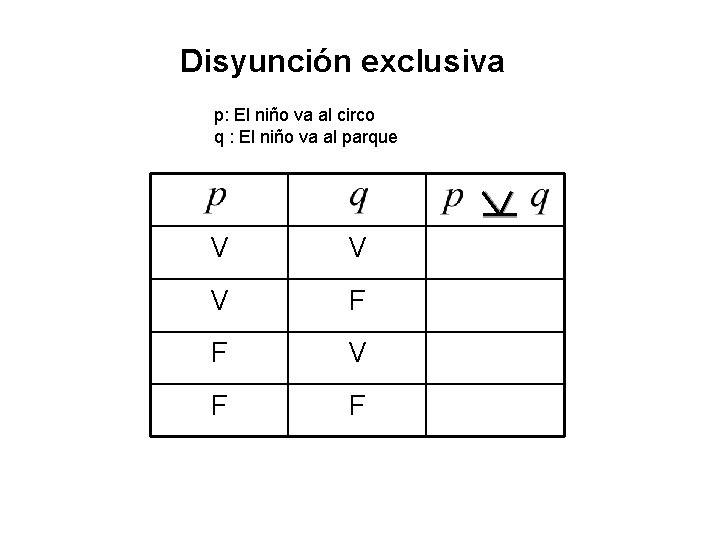
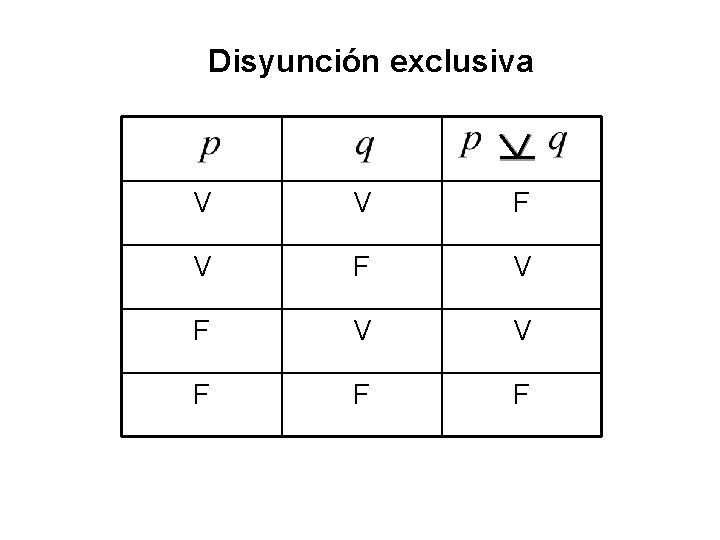
Disyunción exclusiva p: El niño va al circo q : El niño va al parque V V V F F

Disyunción exclusiva V V F V F V V F F F

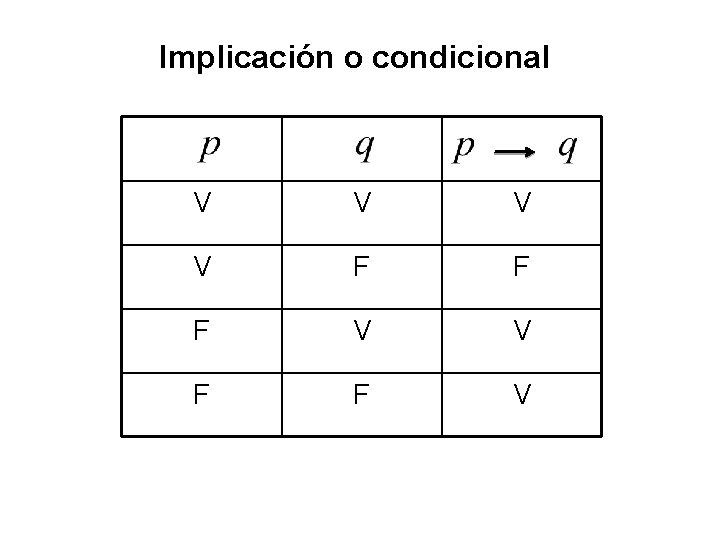
Cuál será el valor de verdad de: • Si 4<6 entonces 16<36 V • Si 4<6 entonces 16>36 F • Si 4>6 entonces 16<36 V • Si 4>6 entonces 16>36 V

Implicación o condicional V V F F F V V F F V

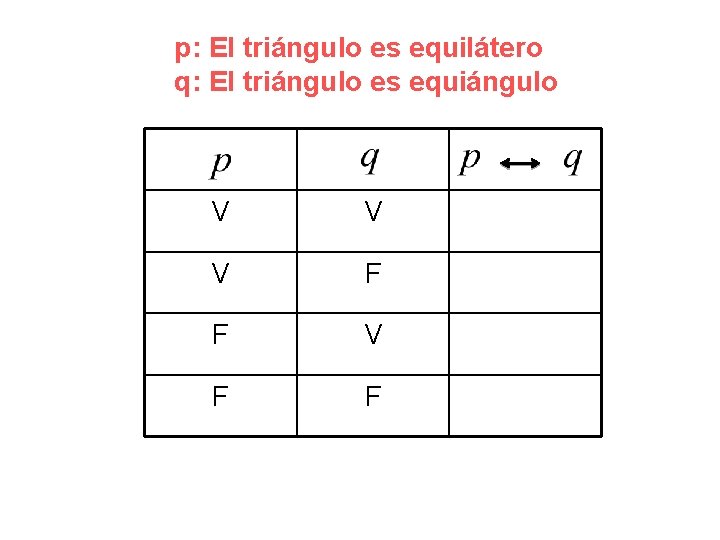
p: El triángulo es equilátero q: El triángulo es equiángulo V V V F F

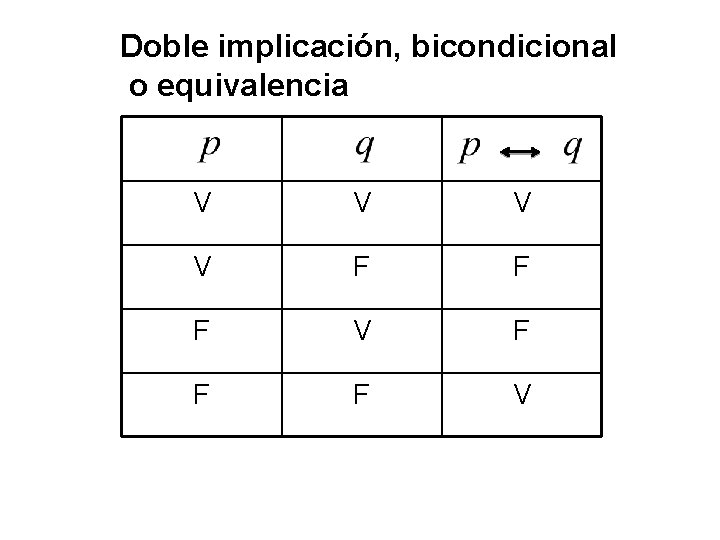
Doble implicación, bicondicional o equivalencia V V F F F V

Una tautología es una proposición cuyo valor de verdad es verdadero independientemente de los valores de verdad de las proposiciones que la componen. Si la proposición es una equivalencia, se dice que las dos proposiciones que ella conecta son lógicamente equivalentes. Si es una implicación, la primera proposición implica lógicamente a la segunda. Ejemplo: V F F V V

Ejemplos de tautologías:

Un predicado es una frase en la cual intervienen variables, se transforma en proposición al ser reemplazadas las variables por constantes. Ejemplos: tiene las orejas largas persigue a los conejos tiene la corta le da rabia

La muerte de Tarzán Nos dan las siguientes proposiciones: a) Los perros que tienen las orejas largas, tienen la corta. b) A los perros que persiguen a los conejos, nunca les da rabia. c) Los perros que no persiguen a los conejos, tienen la cola larga. Hipótesis: Tarzán murió de rabia. Pregunta: ¿Cómo tenía las orejas Tarzán? .

Desarrollo: Como entonces a), b), y c) se pueden escribir en la forma Por lo tanto: Para x= Tarzán es verdadera, de donde se desprende que es verdadera. Por lo tanto Tarzán tenía las orejas cortas

El dilema de la música Si voy a cine o trasnocho, entonces, me enfermo. Si voy a cine o me enfermo, entonces, sufro mucho. Si escucho música en la noche, entonces, trasnocho. Hipótesis: !Yo no sufro!. Pregunta: ¿Escuché música en la noche? .

Desarrollo: Sean: voy a cine trasnocho me enfermo sufro Escucho música Las hipótesis nos conducen a las siguientes proposiciones. Como s es falso, luego es falso. Por lo tanto es falso, y por lo tanto es falso y es falso, de donde es falso, luego: |No escucho música!

El estado de ánimo Si no tomo leche y fumo, entonces, no crezco. Si tomo leche o no crezco, entonces, me pongo triste. Si estoy melancólico, entonces, fumo. Hipótesis: !Estoy contento!. Pregunta: ¿Estaré melancólico? .

Desarrollo: Sean: Tomo leche Fumo Crezco Estoy triste Estoy melancólico Las hipótesis nos conducen a las siguientes proposiciones. Como s es falso, luego es verdadera. Por lo tanto es falso, y por lo tanto es falso y es falso, de donde es falso, luego: |No estoy melancólico|

LA SELECCION IDEAL El entrenador de la Selección Colombia de fútbol ha llamado a los siguientes cuatro jugadores: Adolfo, Bernardo, Carlos y Diego para que jueguen en los puestos de Portero, Defensa Central, Medio Campo y Puntero Derecho aunque no necesariamente en correspondencia con el orden enunciado. Después de observarlos en varios entrenamientos ha llegado a las siguientes conclusiones:

Si Adolfo no es defensa central, Carlos no juega en el medio campo. Si Bernardo juega en el Medio Campo o en la punta derecha, Adolfo es defensa central. Si Carlos no es Portero, Bernardo es puntero derecho. Si Diego juega en el medio campo, Bernardo no es defensa central. Si Diego no es defensa central, Bernardo es defensa central. ¿En que puesto debe jugar cada uno? .

Solución : Sean: A=Adolfo, B=Bernardo, C=Carlos y D=Diego p(x)= x es portero dc(x)= x es defensa central mc(x)= x juega en el medio campo pd(x)= x es puntero derecho. Así el problema escrito en forma simbólica se transforma en:

• dc(A) mc(C) (2) (mc(B) pd(B)) dc(A) (3) p(C) pd(B) (4) mc(D) dc(B) (5) dc(D) dc(B) Si mc(D) es V entonces dc(B) es V, luego dc(B) es F y en (5) tenemos que dc(D) es F, luego dc(D) es V lo cual es imposible ya que mc(D) es V, por lo tanto mc(D) es F.

Supongamos que mc(C) es V, entonces mc(C) es F por (1), luego dc(A) es F y por lo tanto dc(A) es V, de donde dc(B) es F y dc(D) es F, pero esto implica que (4) es F, lo cual es una contradicción. De donde mc(C) es F. Supongamos que mc(B) es V, entonces dc(A) es V por (2), Luego dc(D) es F y dc(B) es F, lo cual nos conduce a una contradicción por (4), por lo tanto mc(B) es F. De lo anterior se deduce que mc(A) es V.

Por otra parte, como mc(B) y dc(A) son F, entonces por (2) se tiene que pd(B) es F. Luego de (3) podemos concluir que p(C) es F, de donde p(C) es V. Como pd(B) es F, pd(A) es F y pd(C) es F entonces pd(D) es V y por exclusión tenemos que dc(B) es V. De lo anterior se concluye que: Adolfo debe jugar en el medio campo Bernardo debe jugar de defensa central Carlos debe jugar de portero Diego debe jugar de puntero derecho.

Dado el predicado p(x) el enunciado Se lee “para todo x p(x)”, y es verdadero si el conjunto de verdad de p(x) es el universo completo. El símbolo se denomina el cuantificador universal Ejemplos:

Dado el predicado p(x) el enunciado Se lee “existe x tal que p(x)”, y es verdadero si el conjunto de verdad de p(x) no es vacío. El símbolo se denomina el cuantificador existencial Ejemplos:

EJERCICIO: Escribir las siguientes proposiciones en forma simbólica: 1. 2. 3. 4. 5. 6. Existe un número primo que no es impar. Existe en Colombia una inteligencia superior. Todos los que no están de acuerdo conmigo son terroristas. Existe un número natural que es el menor de todos Todo número real positivo es un cuadrado. Todos los perros ladran. Dada la proposición condicional p(x) el enunciado Se lee “existe un único x tal que p(x)”, y es verdadero si el conjunto de verdad de p(x) consta exactamente de un solo elemento.

La negación de la proposición es: EJERCICIO: Escribir la negación de las proposiciones dadas en el ejercicio anterior EJERCICIO: Escribir la negación de las siguientes proposiciones:

Definición Un conjunto es una colección de objetos. Ejemplos A = {a, e, i, o, u} B = {blanco, gris, negro} C = {2, 4, 6, 8, 9} D = {x|x es un país de América Latina Extensión y Comprensión Cuando un conjunto es descrito por un propiedad que comparten sus elementos se dice que está determinado por comprensión. Cuando damos una lista explícita de los elementos del conjunto, decimos que está determinado por extensión.

Conjuntos determinados por extensión y por Comprensión A = {x|x es un número primo menor que 50} A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47} B = {x|x es un entero mayor que -3} B = {− 2, − 1, 0, 1, 2, 3, . . . } C = {x|x es un número par y primo} C = {2}

Consideremos el conjunto D = {x | x es par, primo y mayor que 5} El conjunto que no tiene elementos se conoce como el conjunto vacío y se acostumbra a notar por ∅ o { }. OJO {∅} NO es el conjunto vacío, es un conjunto con un elemento.

U

Conjunto Potencia o conjunto de Partes Sea A un conjunto. Definimos la colección P(A) : = {X | X ⊆ A}. Se conoce como el conjunto de Partes de A, o el conjunto Potencia de A. Ejemplos: Sea A = {a, b}. P(A) = {∅, {a}, {b}, {a, b}}. Sea A = {a, b, c}. P(A) = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

Si A ⊆ B entonces P(A) ⊆ P(B). Si A es un conjunto finito con n elementos, entonces P(A) tiene elementos.

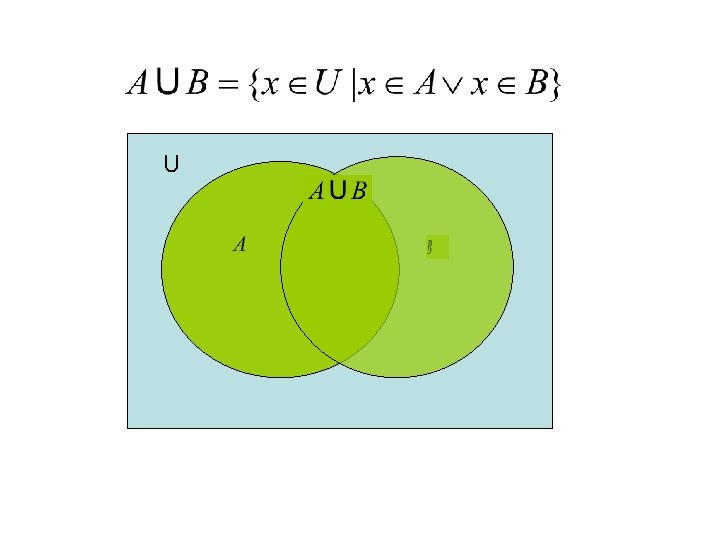
U

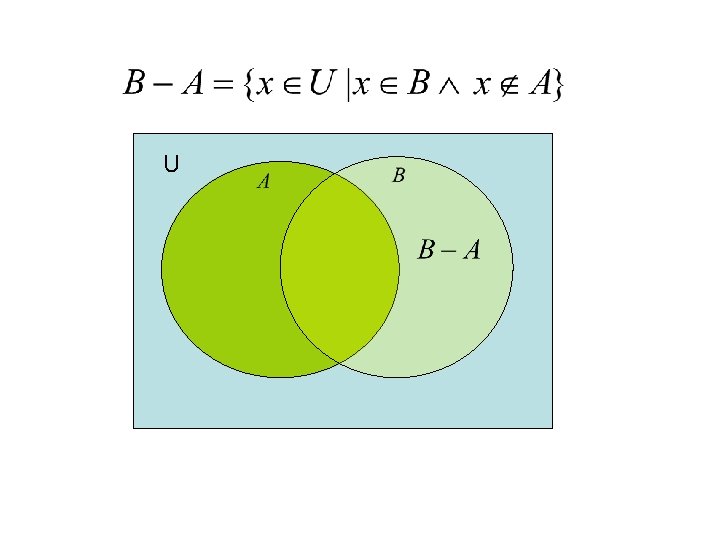
U

U


Algunas propiedades de las operaciones entre conjuntos

Algunas propiedades de las operaciones entre conjuntos

DIAGRAMAS DE VENN Construimos un Diagrama de Venn, tratando en lo posible que exista la mayor cantidad de intersecciones entre los diferentes conjuntos. Ejemplo: Sean los siguientes cuatro conjuntos: A = {1, 3, 5, 7, 9}, B ={1, 2}, C={2, 4, 6, 9} y D={ 5, 6}

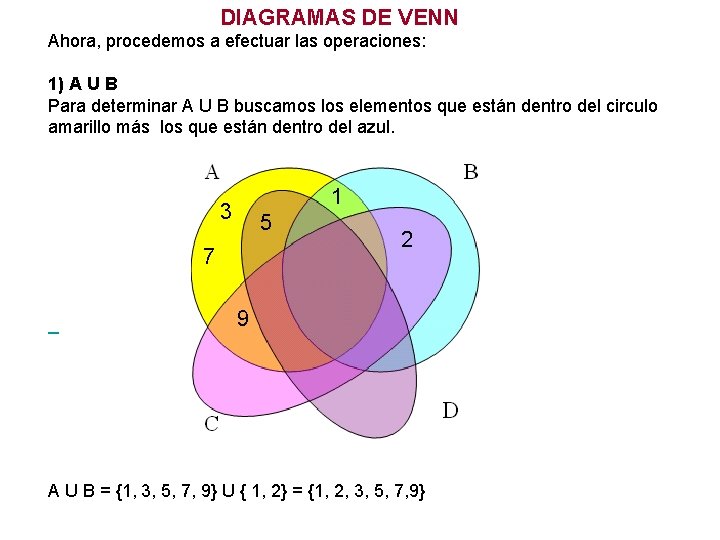
DIAGRAMAS DE VENN Ahora, procedemos a efectuar las operaciones: 1) A U B Para determinar A U B buscamos los elementos que están dentro del circulo amarillo más los que están dentro del azul. 3 1 5 7 2 9 A U B = {1, 3, 5, 7, 9} U { 1, 2} = {1, 2, 3, 5, 7, 9}

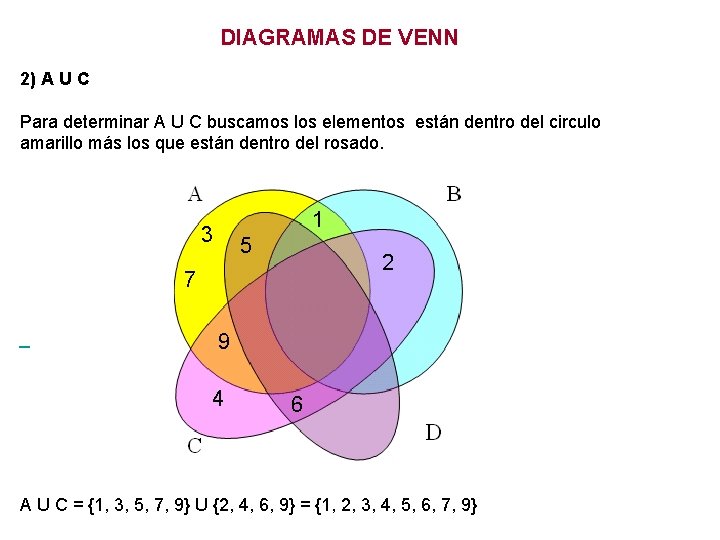
DIAGRAMAS DE VENN 2) A U C Para determinar A U C buscamos los elementos están dentro del circulo amarillo más los que están dentro del rosado. 3 1 5 2 7 9 4 6 A U C = {1, 3, 5, 7, 9} U {2, 4, 6, 9} = {1, 2, 3, 4, 5, 6, 7, 9}

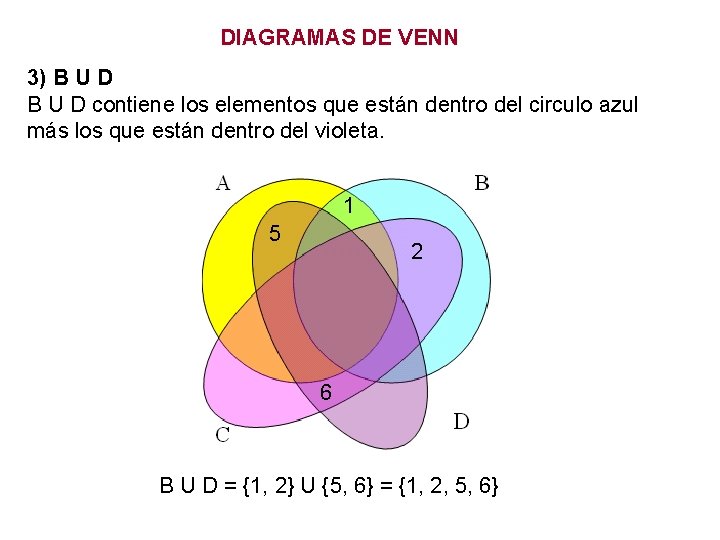
DIAGRAMAS DE VENN 3) B U D contiene los elementos que están dentro del circulo azul más los que están dentro del violeta. 1 5 2 6 B U D = {1, 2} U {5, 6} = {1, 2, 5, 6}

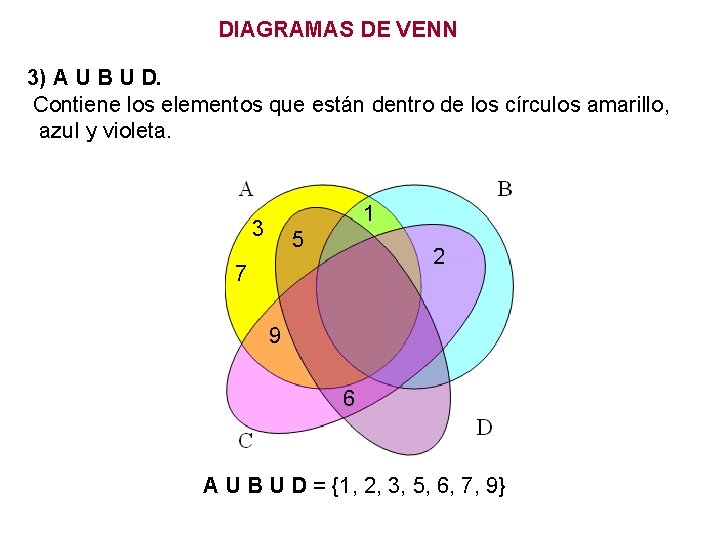
DIAGRAMAS DE VENN 3) A U B U D. Contiene los elementos que están dentro de los círculos amarillo, azul y violeta. 1 3 5 2 7 9 6 A U B U D = {1, 2, 3, 5, 6, 7, 9}

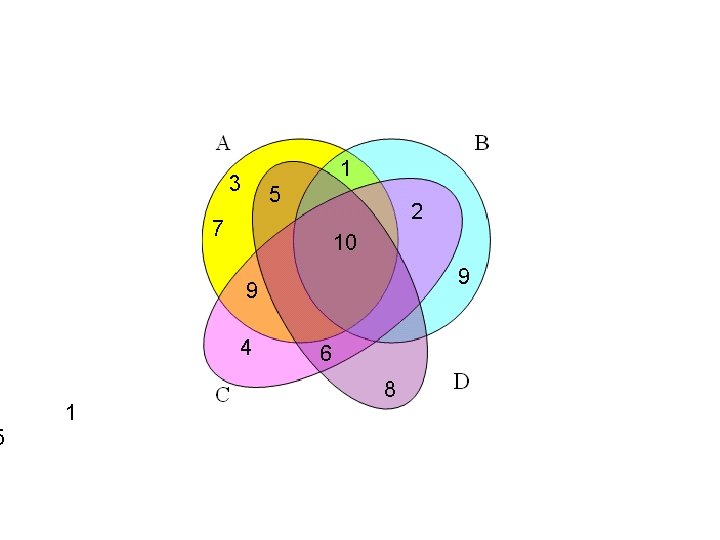
5 1 3 5 2 7 10 9 9 4 1 6 8

A U B C




 Que es una pseudoproposicion
Que es una pseudoproposicion Que es una proposicion
Que es una proposicion Proposición simple.
Proposición simple. Tautología
Tautología Todos os tipos de frases
Todos os tipos de frases Oraciones subordinadas sustantivas declarativas
Oraciones subordinadas sustantivas declarativas Uma frase interrogativa
Uma frase interrogativa Oraciones con la palabra bailarina
Oraciones con la palabra bailarina Frases de ponto de interrogação
Frases de ponto de interrogação Oracion ultima cena
Oracion ultima cena Oración conjunta
Oración conjunta Oracin
Oracin Oracin
Oracin Oracin
Oracin Docibilidad
Docibilidad Oracin
Oracin Ejemplos de conduplicacion
Ejemplos de conduplicacion Oracin
Oracin Oracin
Oracin Oraciones simples y sus clases
Oraciones simples y sus clases Oracion de pensar
Oracion de pensar Oracin
Oracin Oracin
Oracin Una gimnasta agita una cinta con una frecuencia constante
Una gimnasta agita una cinta con una frecuencia constante Frases é todo enunciado de sentido completo
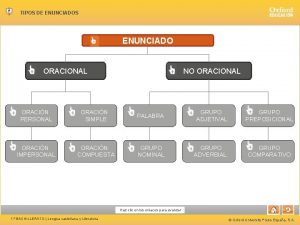
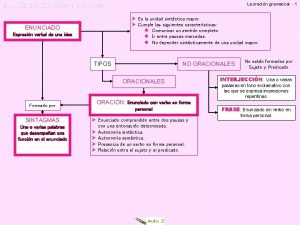
Frases é todo enunciado de sentido completo Enunciado oracional simple
Enunciado oracional simple El texto es un conjunto
El texto es un conjunto Enunciado 93 cnj
Enunciado 93 cnj Del enunciado pero ante todo tienes que cumplir otro viaje
Del enunciado pero ante todo tienes que cumplir otro viaje Ejemplos de enunciado del problema
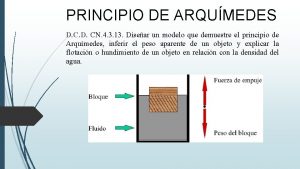
Ejemplos de enunciado del problema Arqumedes
Arqumedes Qué son oraciones unimembres
Qué son oraciones unimembres Conectivos textuais
Conectivos textuais Enunciado cerrado
Enunciado cerrado Ifla
Ifla Enunciado abierto
Enunciado abierto Cuales son los enunciados oracionales
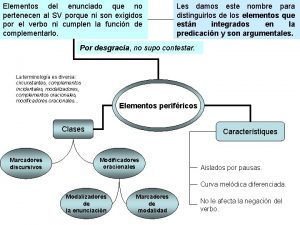
Cuales son los enunciados oracionales Elementos del enunciado
Elementos del enunciado Electromagnetismo
Electromagnetismo Ejemplos de enunciado del problema
Ejemplos de enunciado del problema Enunciado de aa
Enunciado de aa Enunciados teoricos puros y mixtos ejemplos
Enunciados teoricos puros y mixtos ejemplos El enunciado se divide en
El enunciado se divide en Ejemplos de segmentacion geografica
Ejemplos de segmentacion geografica Longitud media del enunciado
Longitud media del enunciado Enunciado proposicional ejemplos
Enunciado proposicional ejemplos Enunciado de nernst-simon
Enunciado de nernst-simon Lenguaje verbal y algebraico
Lenguaje verbal y algebraico Enunciado positivo
Enunciado positivo Infortunios desaciertos y abusos ejemplos
Infortunios desaciertos y abusos ejemplos Base empírica y zona teórica ejemplos
Base empírica y zona teórica ejemplos Enunciado correcto
Enunciado correcto Enunciado gsa
Enunciado gsa Enunciado normativo
Enunciado normativo Selecciona el enunciado que podría corresponder al sistema
Selecciona el enunciado que podría corresponder al sistema Segunda lei da termodinamica enunciado
Segunda lei da termodinamica enunciado