Transformations of Functions and their Graphs Joseph Perone























- Slides: 79

Transformations of Functions and their Graphs Joseph Perone Precalculus, 2013 Adapted from Mary Dwyer Wolfe, Ph. D. , Macon State College

Linear Transformations These are the common linear transformations used in high school algebra courses. Translations (shifts) Reflections Dilations (stretches or shrinks) We examine the mathematics: § Graphically § Numerically § Symbolically § Verbally

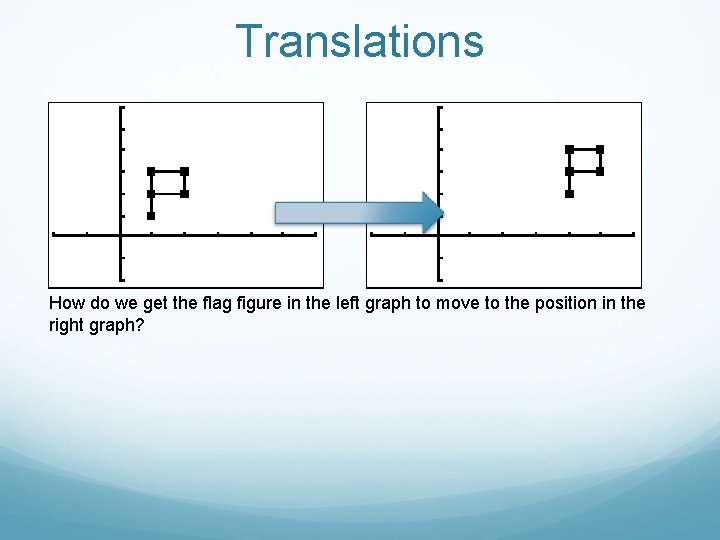
Translations

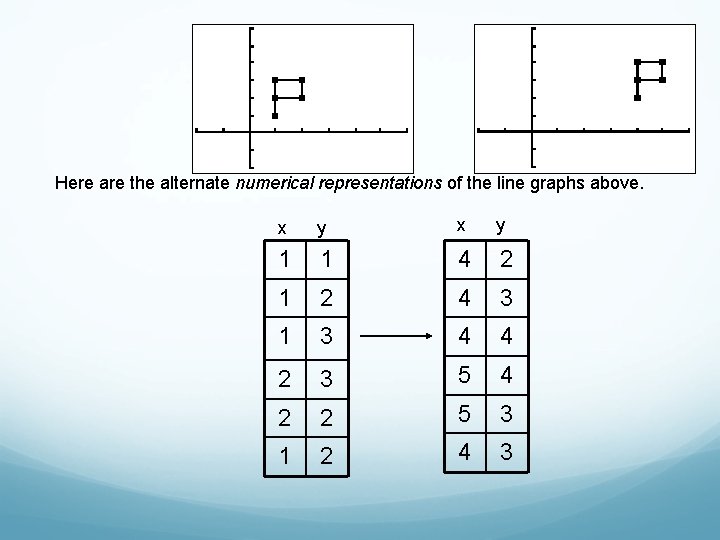
Translations How do we get the flag figure in the left graph to move to the position in the right graph?

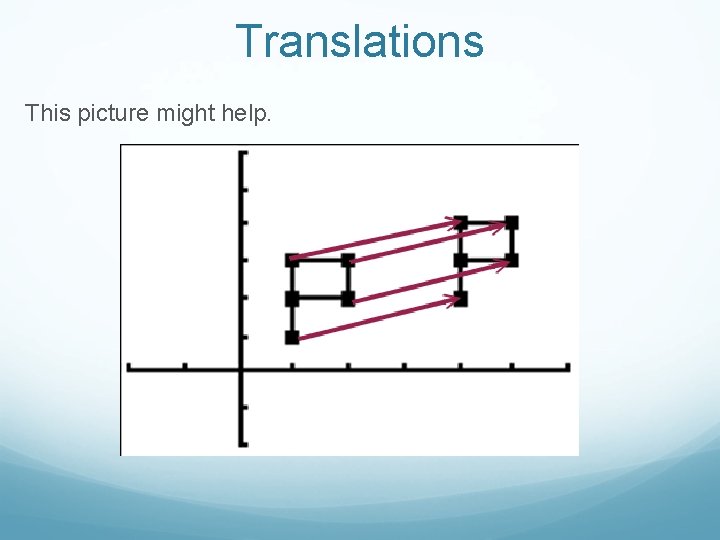
Translations This picture might help.

Here are the alternate numerical representations of the line graphs above. x y 1 1 4 2 1 2 4 3 1 3 4 4 2 3 5 4 2 2 5 3 1 2 4 3

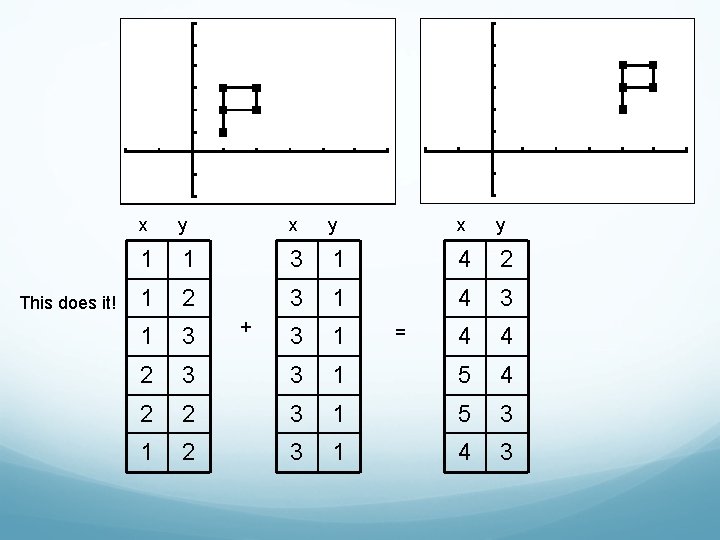
This does it! x y x y 1 1 3 1 4 2 1 2 3 1 4 3 1 3 3 1 4 4 2 3 3 1 5 4 2 2 3 1 5 3 1 2 3 1 4 3 + =

Translations Alternately, we could first add 1 to the y-coordinates and then 3 to the x-coordinates to arrive at the final image.

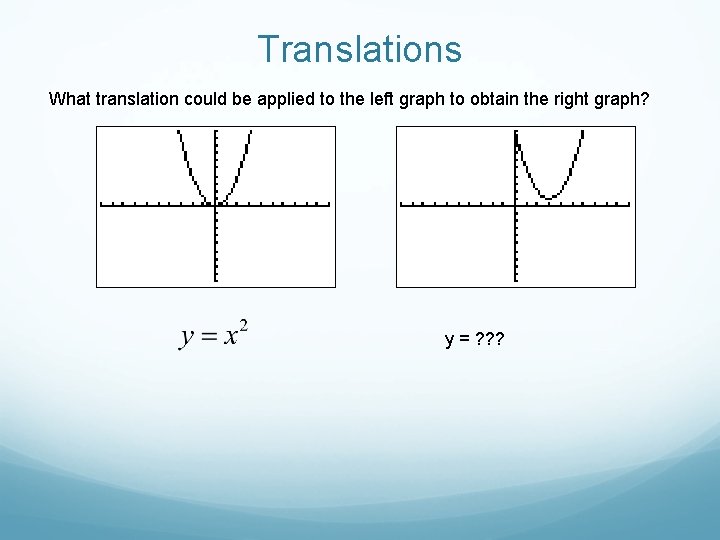
Translations What translation could be applied to the left graph to obtain the right graph? y = ? ? ?

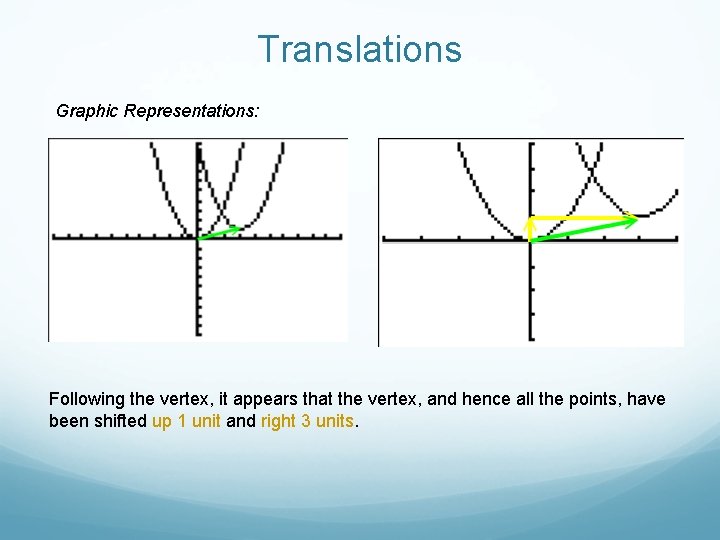
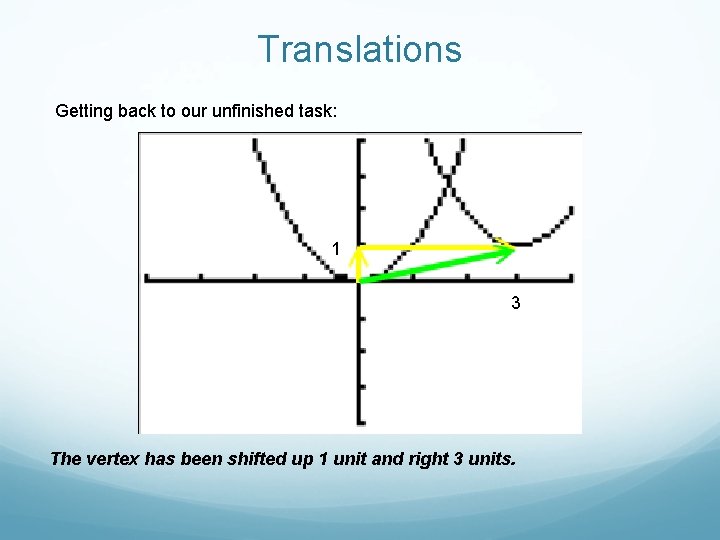
Translations Graphic Representations: Following the vertex, it appears that the vertex, and hence all the points, have been shifted up 1 unit and right 3 units.

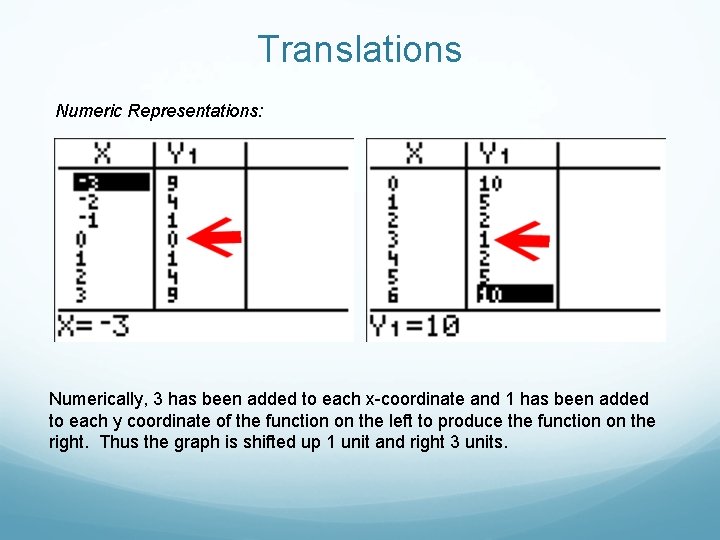
Translations Numeric Representations: Numerically, 3 has been added to each x-coordinate and 1 has been added to each y coordinate of the function on the left to produce the function on the right. Thus the graph is shifted up 1 unit and right 3 units.

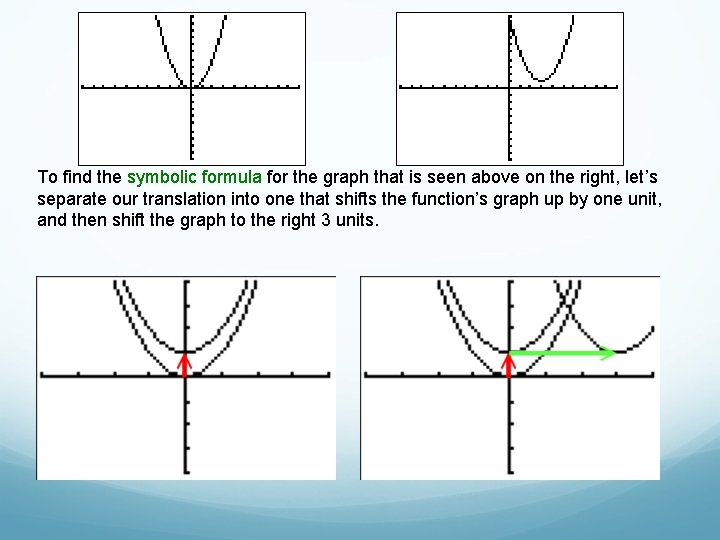
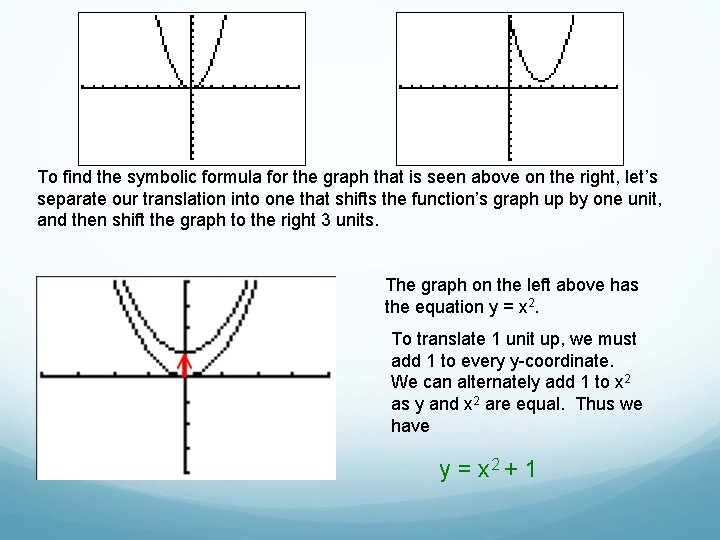
To find the symbolic formula for the graph that is seen above on the right, let’s separate our translation into one that shifts the function’s graph up by one unit, and then shift the graph to the right 3 units.

To find the symbolic formula for the graph that is seen above on the right, let’s separate our translation into one that shifts the function’s graph up by one unit, and then shift the graph to the right 3 units. The graph on the left above has the equation y = x 2. To translate 1 unit up, we must add 1 to every y-coordinate. We can alternately add 1 to x 2 as y and x 2 are equal. Thus we have y = x 2 + 1

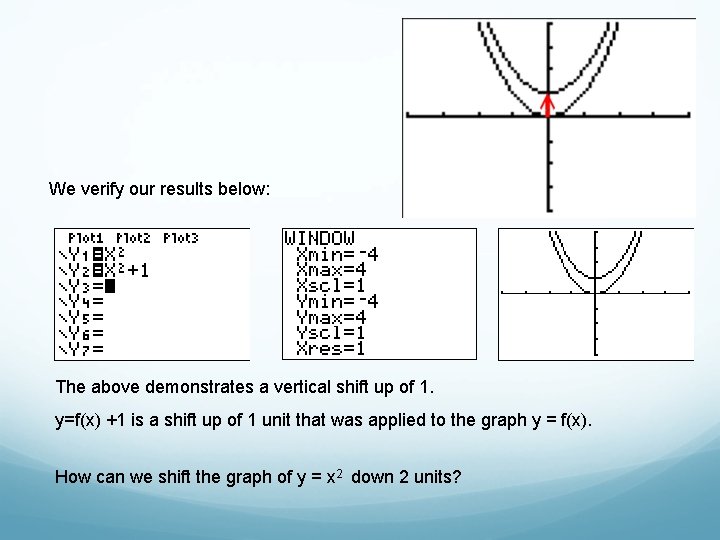
We verify our results below: The above demonstrates a vertical shift up of 1. y=f(x) +1 is a shift up of 1 unit that was applied to the graph y = f(x). How can we shift the graph of y = x 2 down 2 units?

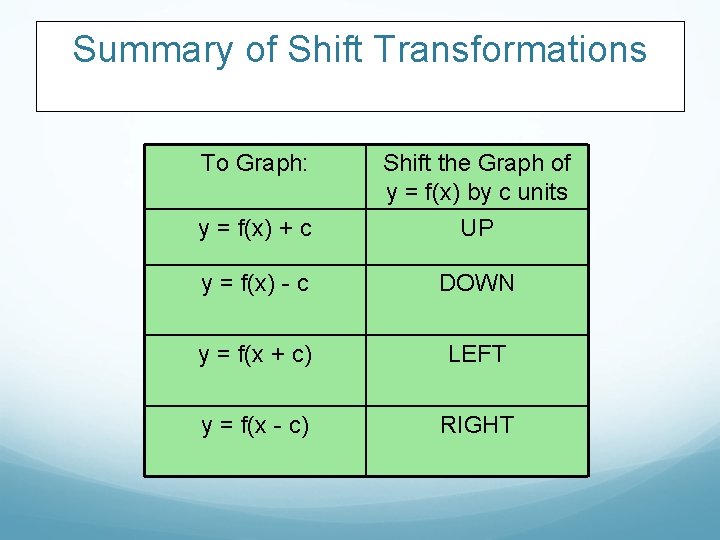
Translations Did you guess to subtract 2 units? We verify our results below: The above demonstrates a vertical shift down of 2. y = f(x) - 2 is a shift down 2 unit to the graph y = f(x) Vertical Shifts If k is a real number and y = f(x) is a function, we say that the graph of y = f(x) + k is the graph of f(x) shifted vertically by k units. If k > 0 then the shift is upward and if k < 0, the shift is downward.

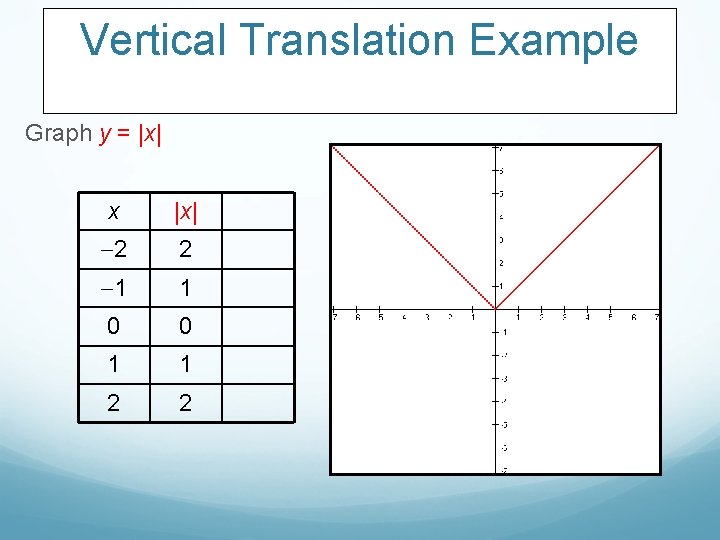
Vertical Translation Example Graph y = |x| x |x| 2 2 1 1 0 0 1 1 2 2

Aside: y = |x| on the TI 83/84

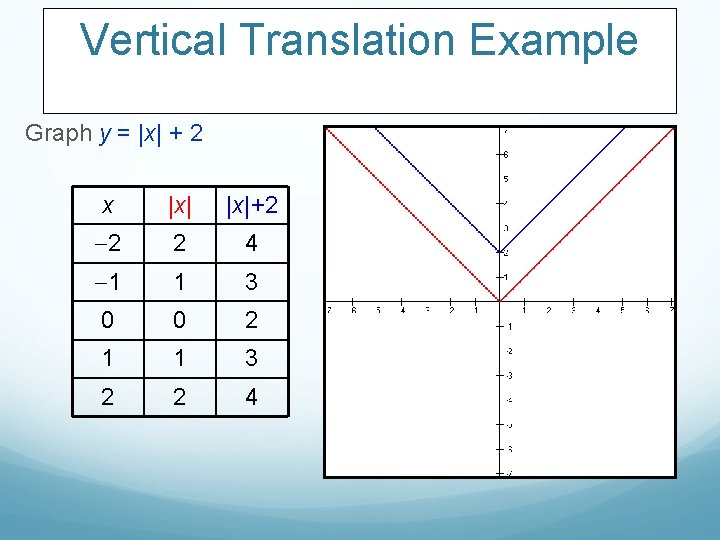
Vertical Translation Example Graph y = |x| + 2 x |x|+2 2 2 4 1 1 3 0 0 2 1 1 3 2 2 4

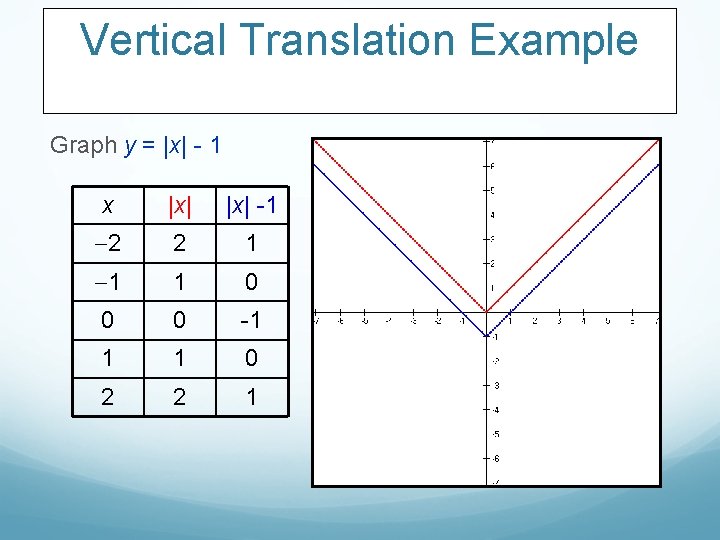
Vertical Translation Example Graph y = |x| - 1 x |x| -1 2 2 1 1 1 0 0 0 -1 1 1 0 2 2 1

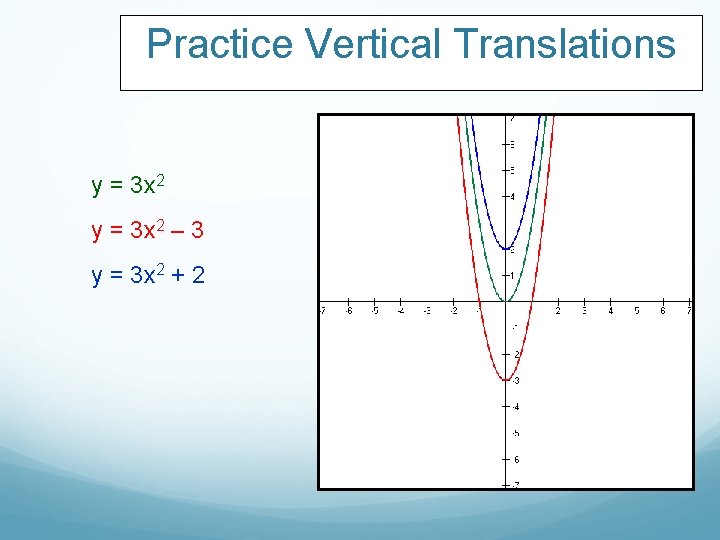
Practice Vertical Translations y = 3 x 2 Now shift the formula vertically up and down. Sketch the graph. Let’s say you chose: 3 down 2 up.

Practice Vertical Translations y = 3 x 2 – 3 y = 3 x 2 + 2

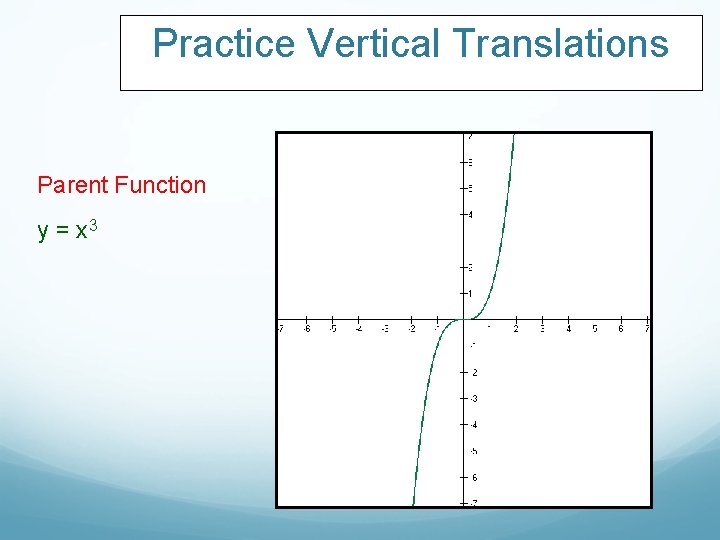
Practice Vertical Translations Parent Function y = x 3

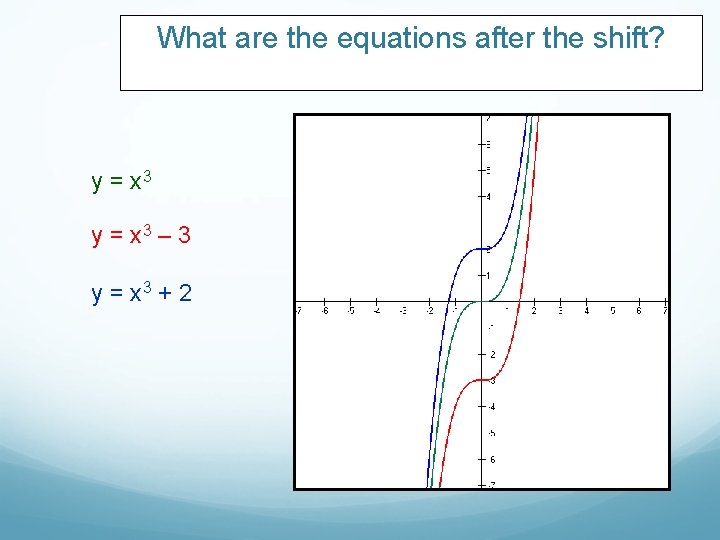
What are the equations after the shift? y = x 3 – 3 y = x 3 + 2

Translations Getting back to our unfinished task: 1 3 The vertex has been shifted up 1 unit and right 3 units.

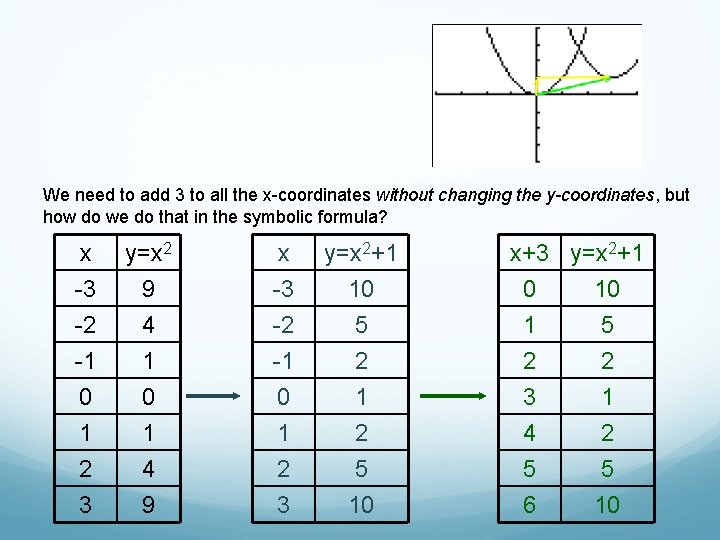
Starting with y = x 2 we know that adding 1 to x 2, that is y = x 2 +1 shifts the graph up 1 unit. Now, how do we also shift the graph 3 units to the right (horizontal shift)? We need to add 3 to all the x-coordinates without changing the y-coordinates, but how do we do that in the symbolic formula?

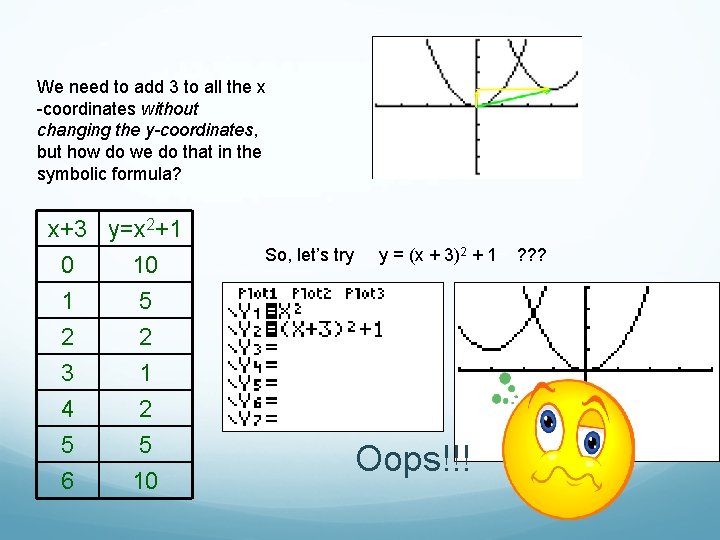
We need to add 3 to all the x-coordinates without changing the y-coordinates, but how do we do that in the symbolic formula? x -3 -2 -1 y=x 2 9 4 1 x -3 -2 -1 y=x 2+1 10 5 2 0 1 2 3 0 1 4 9 0 1 2 3 1 2 5 10 x+3 y=x 2+1 0 10 1 5 2 2 3 4 5 6 1 2 5 10

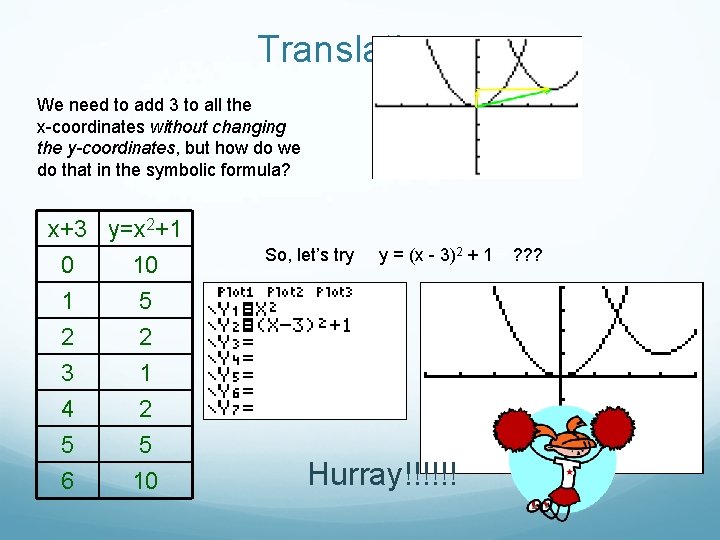
We need to add 3 to all the x -coordinates without changing the y-coordinates, but how do we do that in the symbolic formula? x+3 y=x 2+1 0 10 1 5 2 2 3 4 5 6 1 2 5 10 So, let’s try y = (x + 3)2 + 1 Oops!!! ? ? ?

Translations We need to add 3 to all the x-coordinates without changing the y-coordinates, but how do we do that in the symbolic formula? x+3 y=x 2+1 0 10 1 5 2 2 3 4 5 6 1 2 5 10 So, let’s try y = (x - 3)2 + 1 Hurray!!!!!! ? ? ?

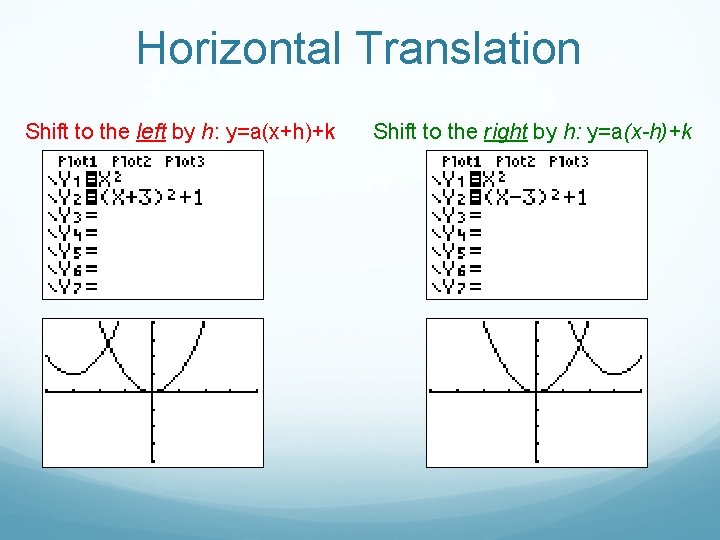
Horizontal Translation Shift to the left by h: y=a(x+h)+k Shift to the right by h: y=a(x-h)+k

Translations Horizontal Shifts If h is a real number and y = f(x) is a function, we say that the graph of y = f(x - h) is the graph of f(x) shifted horizontally by h units. If h follows a minus sign, then the shift is right and if h follows a + sign, then the shift is left. Vertical Shifts If k is a real number and y = f(x) is a function, we say that the graph of y = f(x) + k is the graph of f(x) shifted vertically by k units. If k > 0 then the shift is upward and if k < 0, the shift is downward.

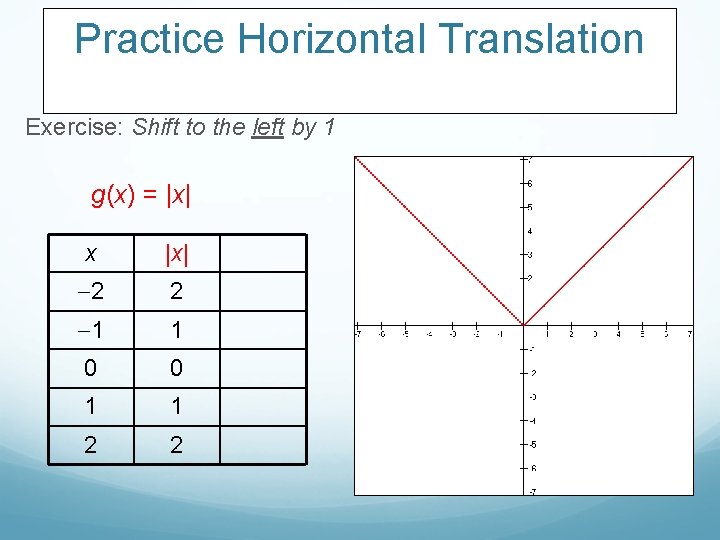
Practice Horizontal Translation Exercise: Shift to the left by 1 g(x) = |x| x |x| 2 2 1 1 0 0 1 1 2 2

Practice Horizontal Translation Graph g(x) = |x + 1| x |x| |x + 1| 2 2 1 1 1 0 0 0 1 1 1 2 2 2 3 What if we shifted g(x)=|x| by 2 to the right?

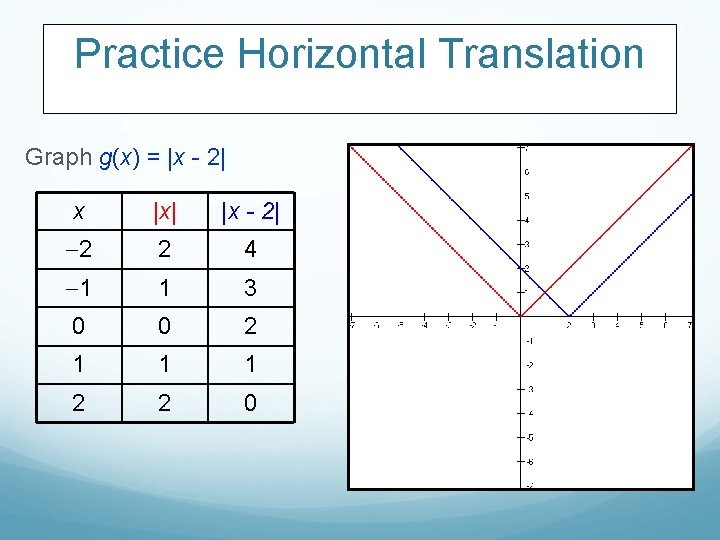
Practice Horizontal Translation Graph g(x) = |x - 2| x |x| |x - 2| 2 2 4 1 1 3 0 0 2 1 1 1 2 2 0

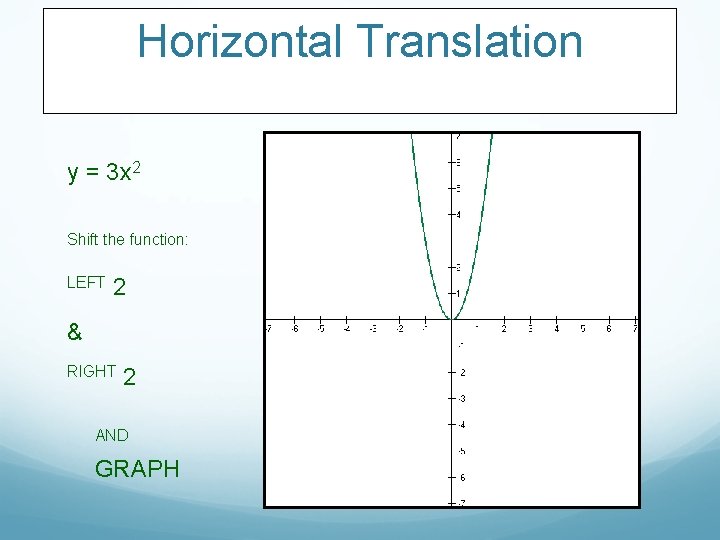
Horizontal Translation y = 3 x 2 Shift the function: LEFT 2 & RIGHT 2 AND GRAPH

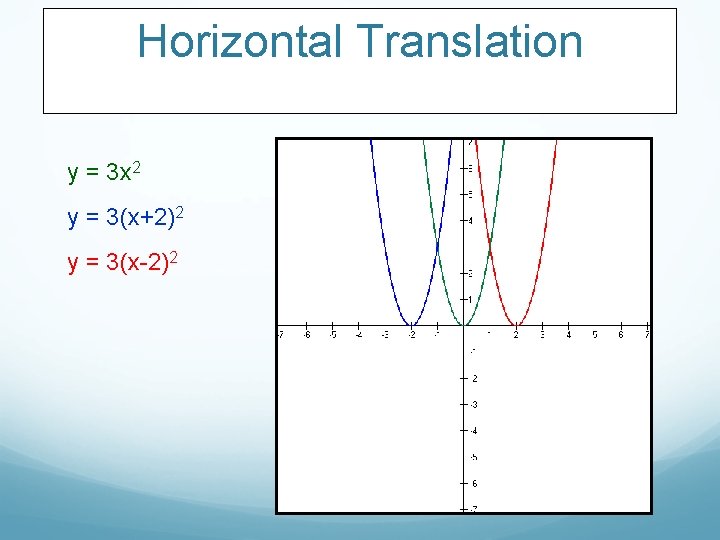
Horizontal Translation y = 3 x 2 y = 3(x+2)2 y = 3(x-2)2

Summary of Shift Transformations To Graph: Shift the Graph of y = f(x) by c units y = f(x) + c UP y = f(x) - c DOWN y = f(x + c) LEFT y = f(x - c) RIGHT

Translations – Combining Shifts Investigate Vertex form of a Quadratic Function: y = x 2 + bx + c y = x 2 y = (x – 3)2 + 1 vertex: (0, 0) vertex: (3, 1) Vertex Form of a Quadratic Function (when a = 1): The quadratic function: has vertex (h, k). y = a(x – h)2 + k

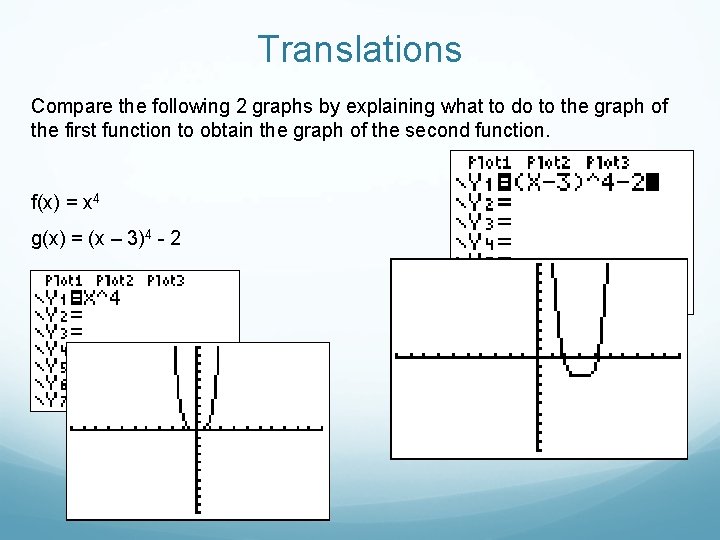
Translations Compare the following 2 graphs by explaining what to do to the graph of the first function to obtain the graph of the second function. f(x) = x 4 g(x) = (x – 3)4 - 2

Reflections

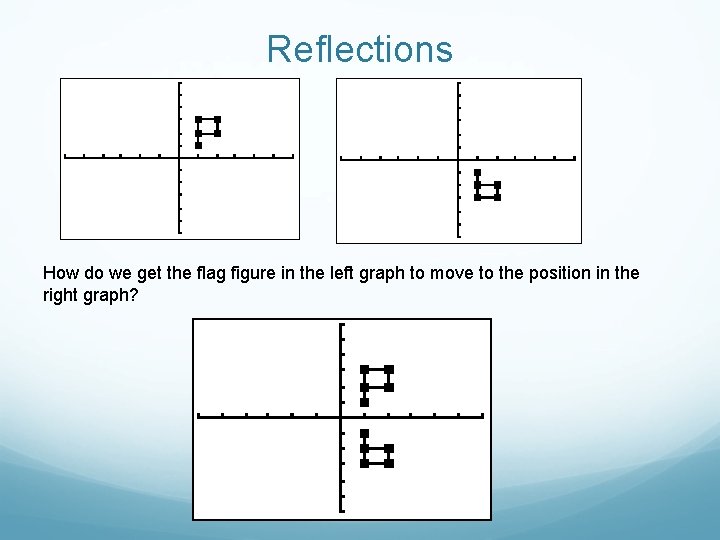
Reflections How do we get the flag figure in the left graph to move to the position in the right graph?

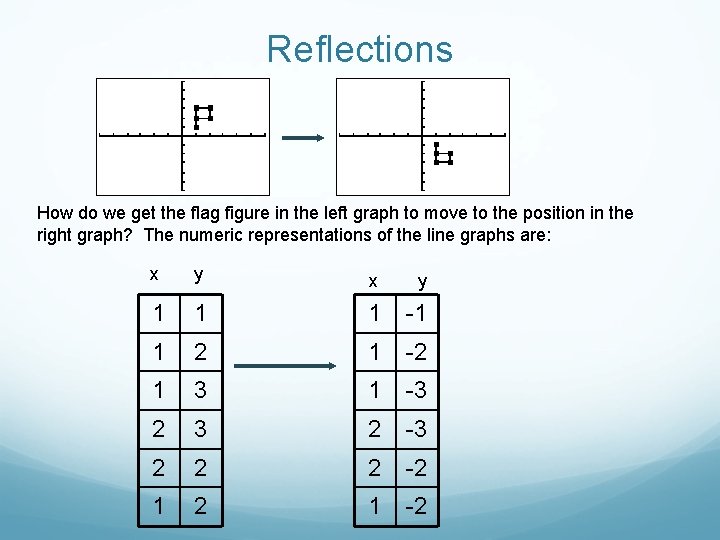
Reflections How do we get the flag figure in the left graph to move to the position in the right graph? The numeric representations of the line graphs are: x y 1 1 1 -1 1 2 1 -2 1 3 1 -3 2 2 2 -2 1 -2

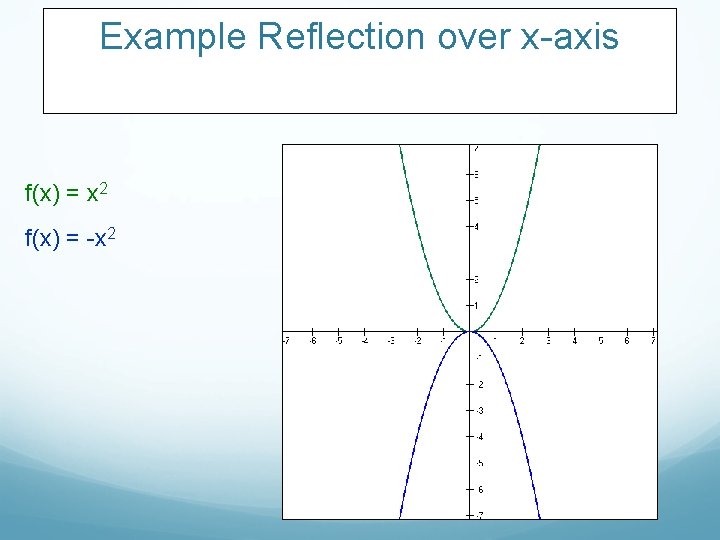
Reflections So how should we change the equation of the function, y = x 2 so that the result will be its reflection (across the x-axis)? Try y = - (x 2) or simply y = - x 2 (Note: - 22 = - 4 while (-2)2 = 4)

Reflection: (across the x-axis) The graph of the function, y = - f(x) is the reflection of the graph of the function y = f(x).

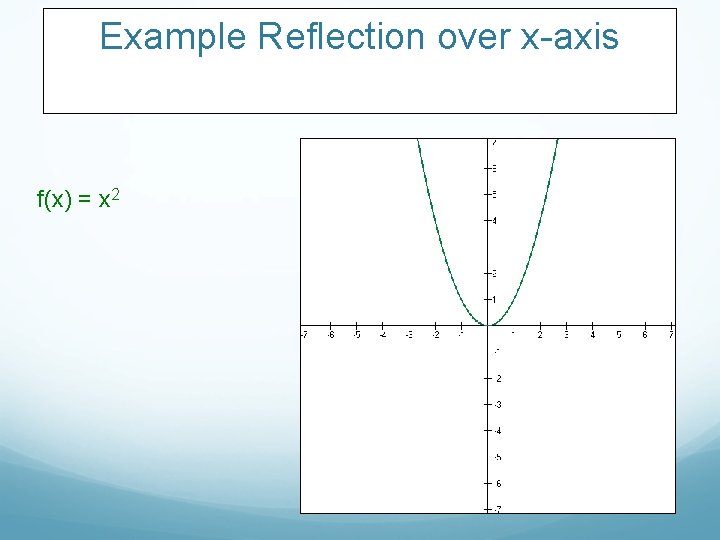
Example Reflection over x-axis f(x) = x 2

Example Reflection over x-axis f(x) = x 2 f(x) = -x 2

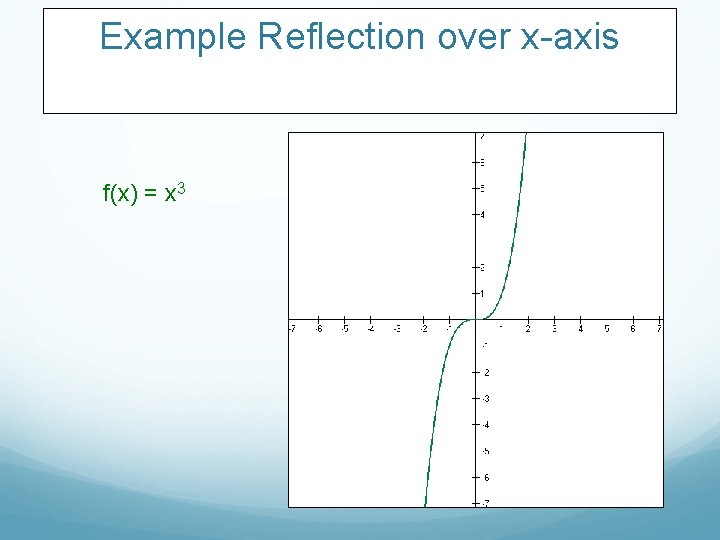
Example Reflection over x-axis f(x) = x 3

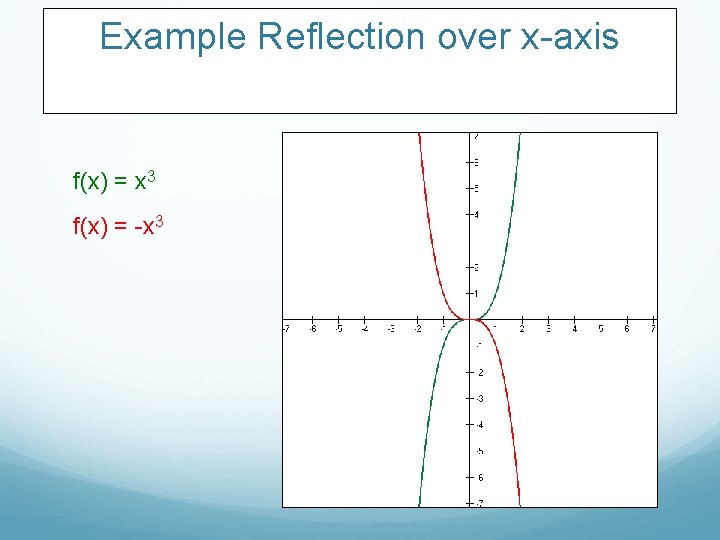
Example Reflection over x-axis f(x) = x 3 f(x) = -x 3

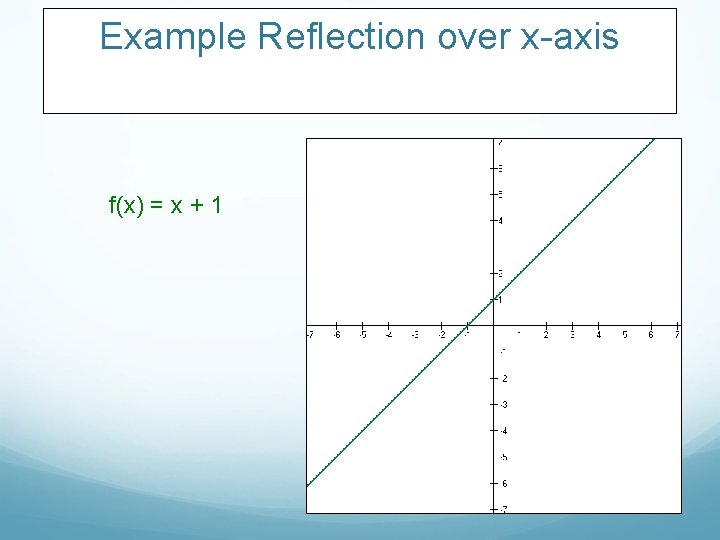
Example Reflection over x-axis f(x) = x + 1

Example Reflection over x-axis f(x) = x + 1 f(x) = -(x + 1) = -x - 1

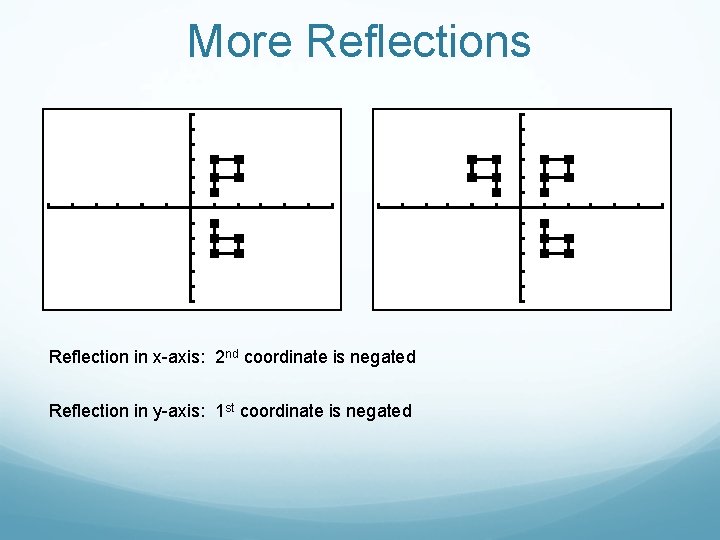
More Reflections Reflection in x-axis: 2 nd coordinate is negated Reflection in y-axis: 1 st coordinate is negated

Reflection: (across the x-axis) The graph of the function, y = - f(x) is the reflection of the graph of the function y = f(x). Reflection: (across the y-axis) The graph of the function, y = f(-x) is the reflection of the graph of the function y = f(x).

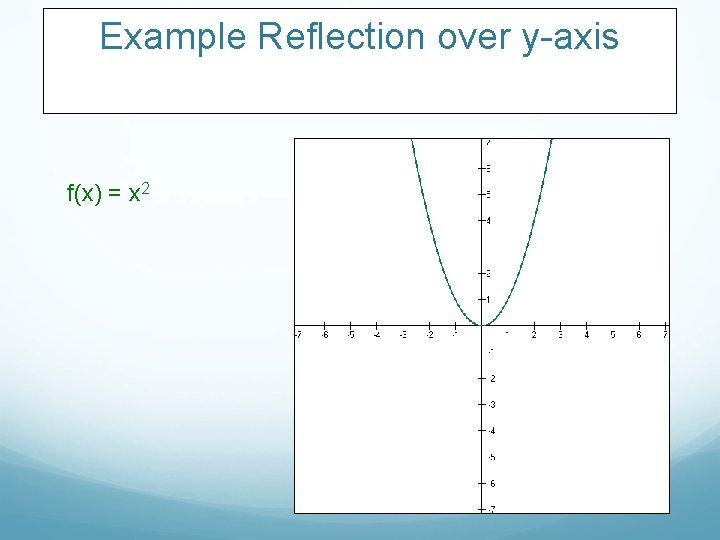
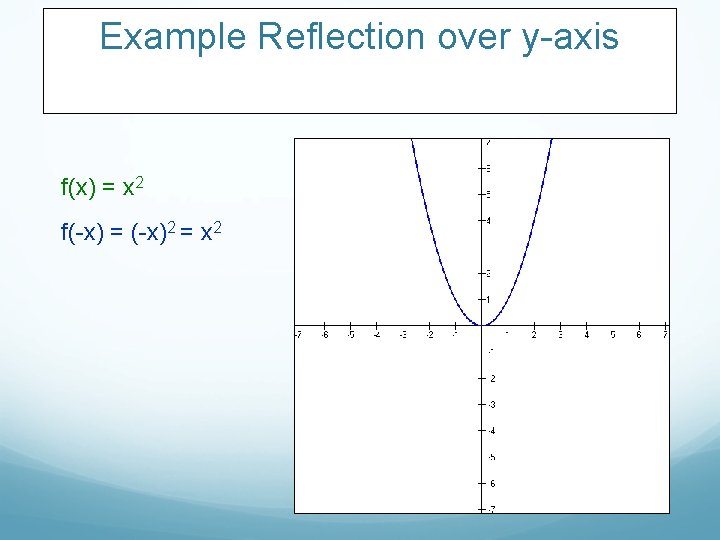
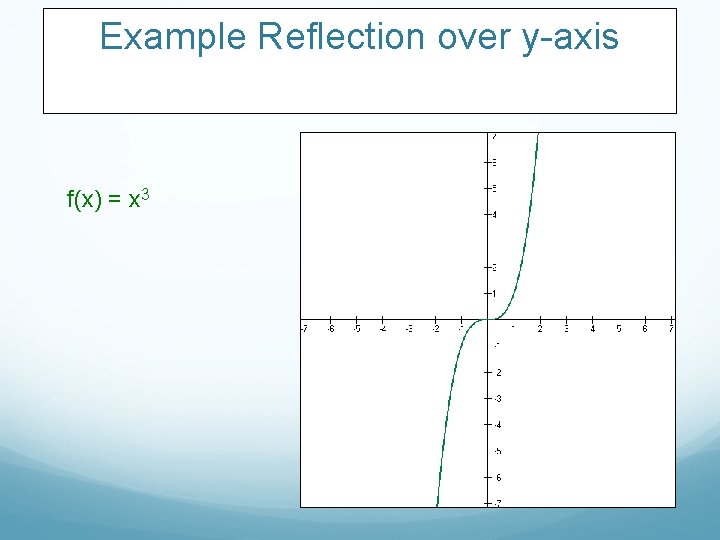
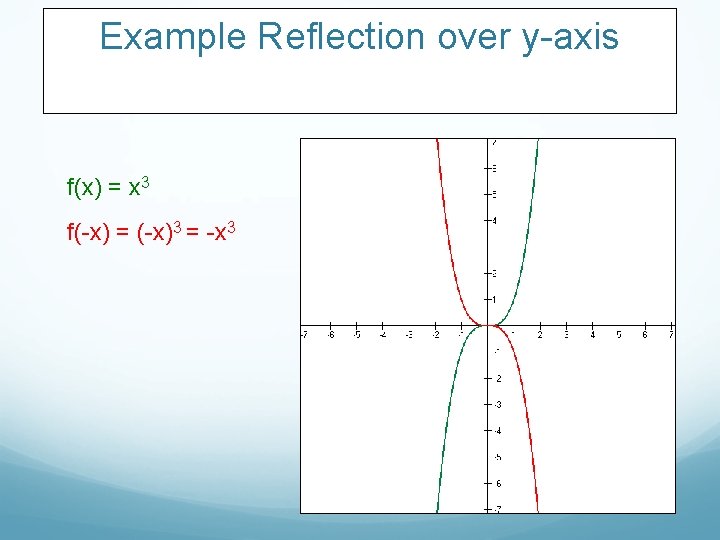
Example Reflection over y-axis f(x) = x 2

Example Reflection over y-axis f(x) = x 2 f(-x) = (-x)2 = x 2

Example Reflection over y-axis f(x) = x 3

Example Reflection over y-axis f(x) = x 3 f(-x) = (-x)3 = -x 3

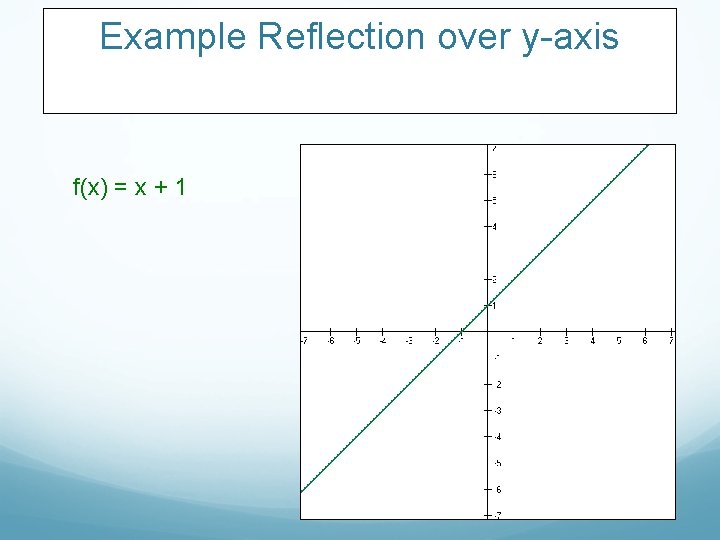
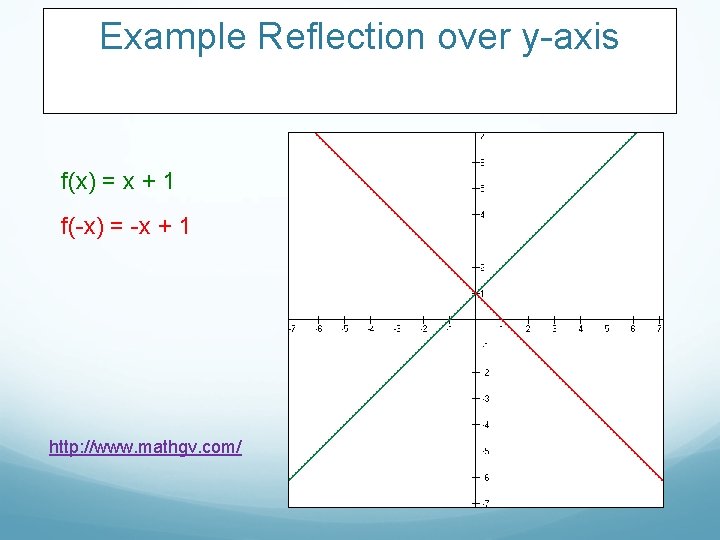
Example Reflection over y-axis f(x) = x + 1

Example Reflection over y-axis f(x) = x + 1 f(-x) = -x + 1 http: //www. mathgv. com/

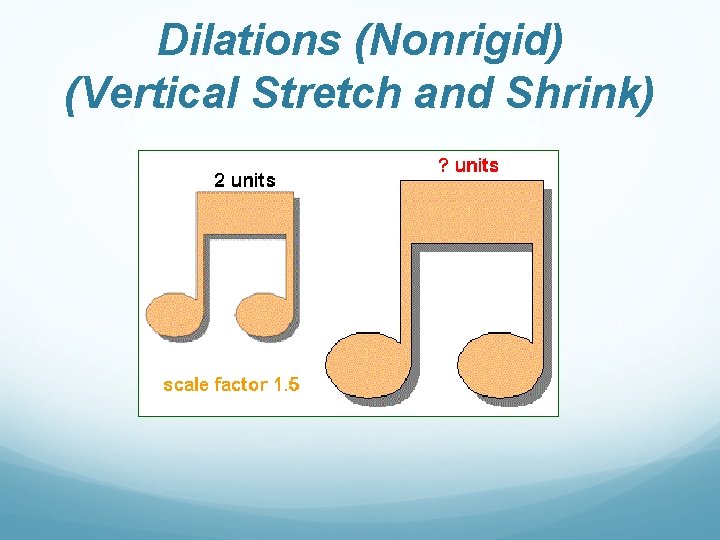
Dilations (Nonrigid) (Vertical Stretch and Shrink)

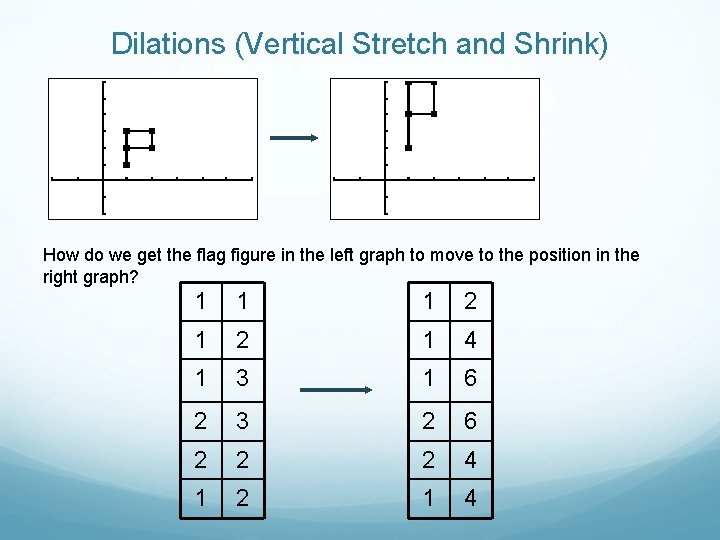
Dilations (Vertical Stretch and Shrink) How do we get the flag figure in the left graph to move to the position in the right graph? 1 1 1 2 1 4 1 3 1 6 2 3 2 6 2 2 2 4 1 2 1 4

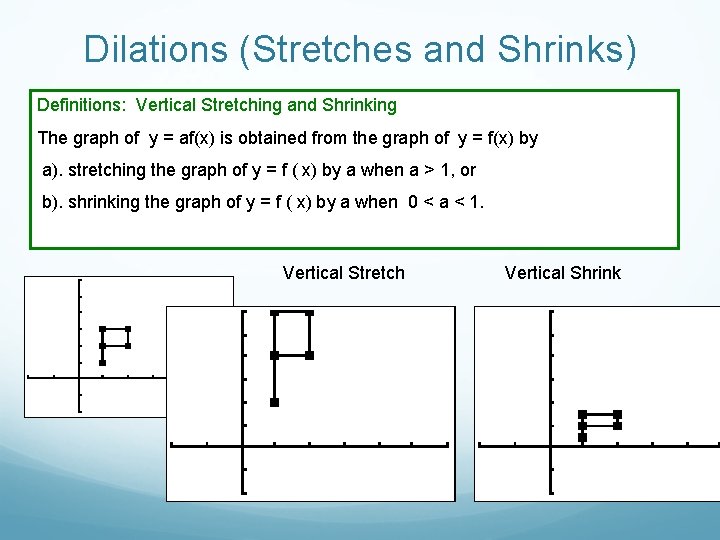
Dilations (Stretches and Shrinks) Definitions: Vertical Stretching and Shrinking The graph of y = af(x) is obtained from the graph of y = f(x) by a). stretching the graph of y = f ( x) by a when a > 1, or b). shrinking the graph of y = f ( x) by a when 0 < a < 1. Vertical Stretch Vertical Shrink

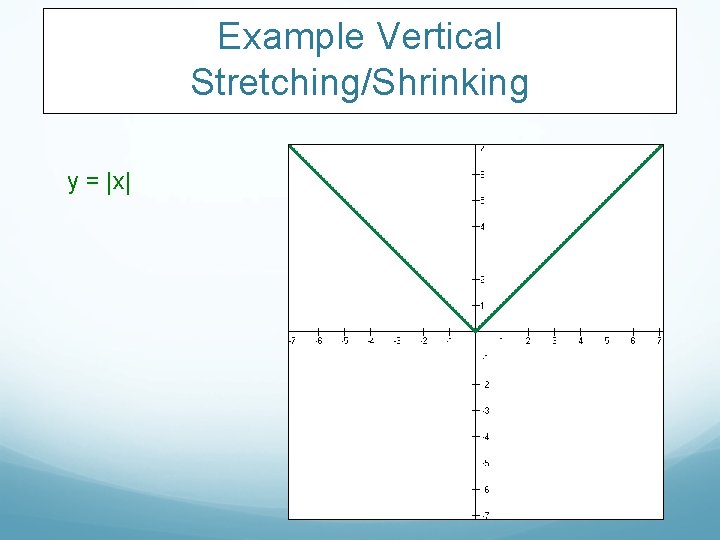
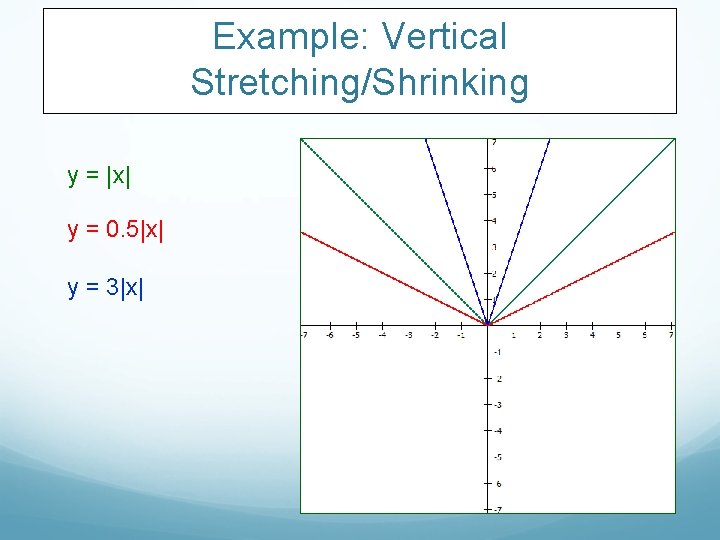
Example Vertical Stretching/Shrinking y = |x|

Example: Vertical Stretching/Shrinking y = |x| y = 0. 5|x| y = 3|x|

What is this? Base Function y = |x| y = ? ? y = -2|x -1| + 4

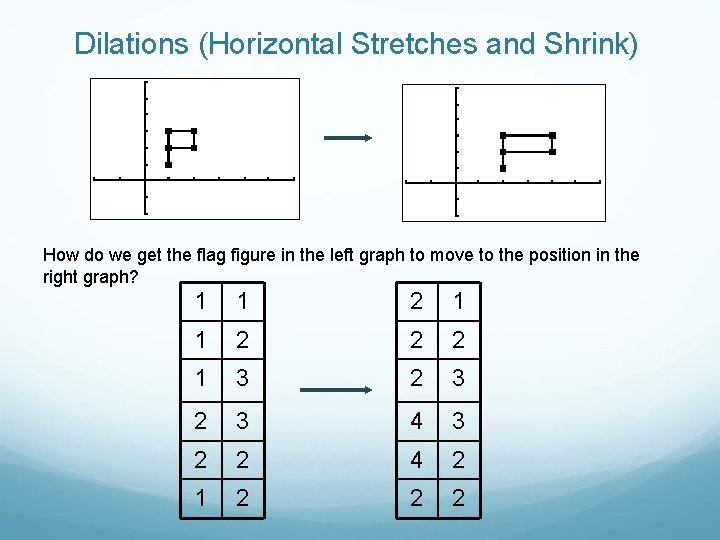
Dilations (Horizontal Stretches and Shrink) How do we get the flag figure in the left graph to move to the position in the right graph? 1 1 2 2 2 1 3 2 3 4 3 2 2 4 2 1 2 2 2

Multiple Transformations Procedure: Multiple Transformations Graph a function involving more than one transformation in the following order: 1. Horizontal translation 2. Stretching or shrinking 3. Reflecting 4. Vertical translation

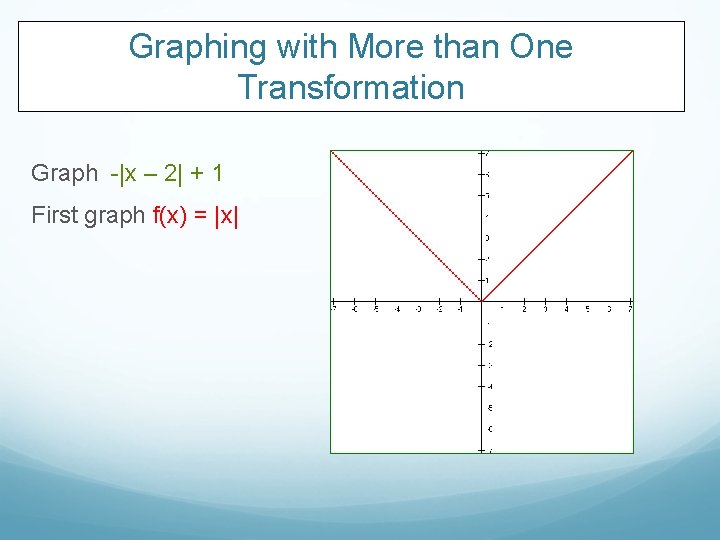
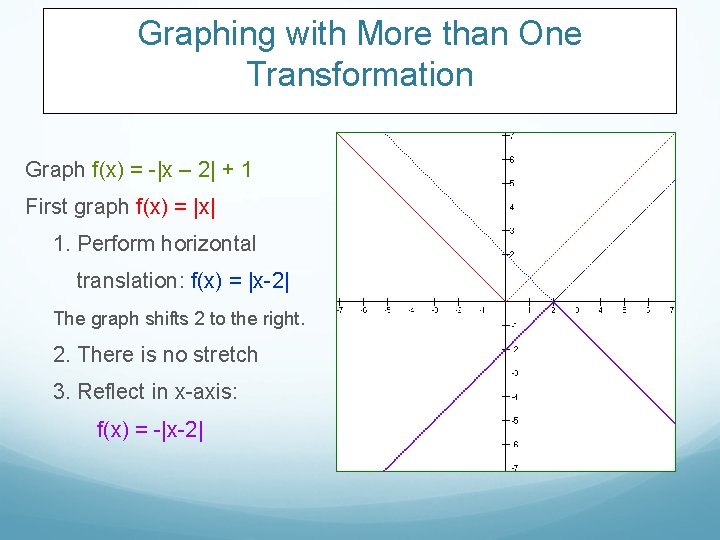
Graphing with More than One Transformation Graph -|x – 2| + 1 First graph f(x) = |x|

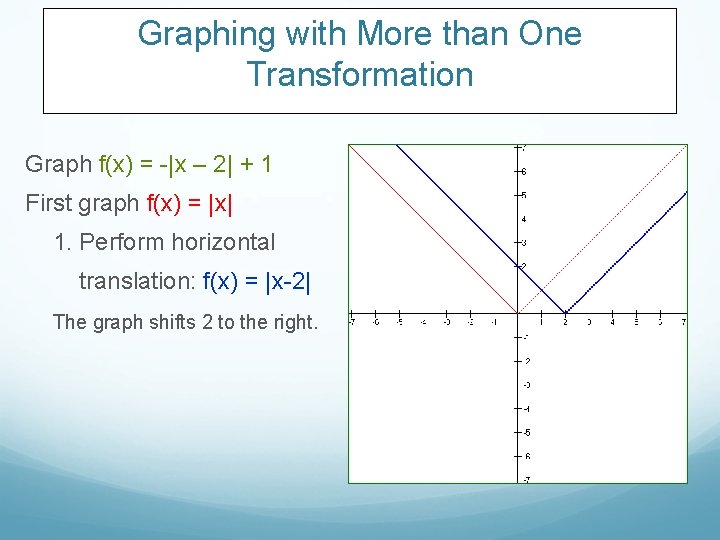
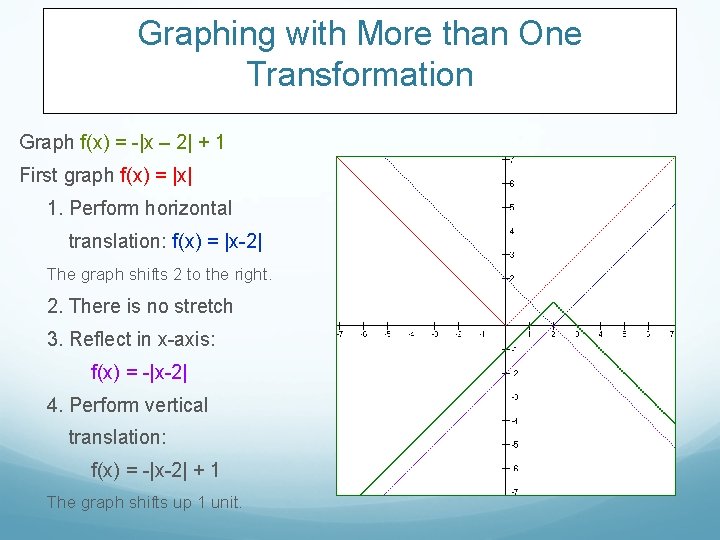
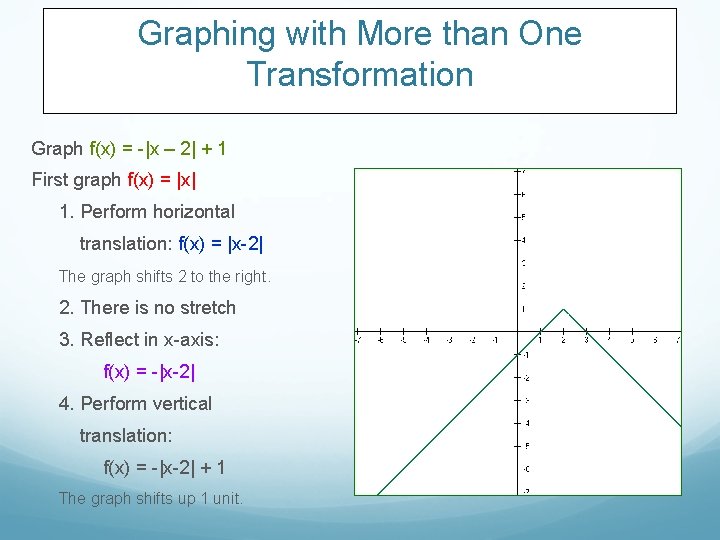
Graphing with More than One Transformation Graph f(x) = -|x – 2| + 1 First graph f(x) = |x| 1. Perform horizontal translation: f(x) = |x-2| The graph shifts 2 to the right.

Graphing with More than One Transformation Graph f(x) = -|x – 2| + 1 First graph f(x) = |x| 1. Perform horizontal translation: f(x) = |x-2| The graph shifts 2 to the right. 2. There is no stretch 3. Reflect in x-axis: f(x) = -|x-2|

Graphing with More than One Transformation Graph f(x) = -|x – 2| + 1 First graph f(x) = |x| 1. Perform horizontal translation: f(x) = |x-2| The graph shifts 2 to the right. 2. There is no stretch 3. Reflect in x-axis: f(x) = -|x-2| 4. Perform vertical translation: f(x) = -|x-2| + 1 The graph shifts up 1 unit.

Graphing with More than One Transformation Graph f(x) = -|x – 2| + 1 First graph f(x) = |x| 1. Perform horizontal translation: f(x) = |x-2| The graph shifts 2 to the right. 2. There is no stretch 3. Reflect in x-axis: f(x) = -|x-2| 4. Perform vertical translation: f(x) = -|x-2| + 1 The graph shifts up 1 unit.

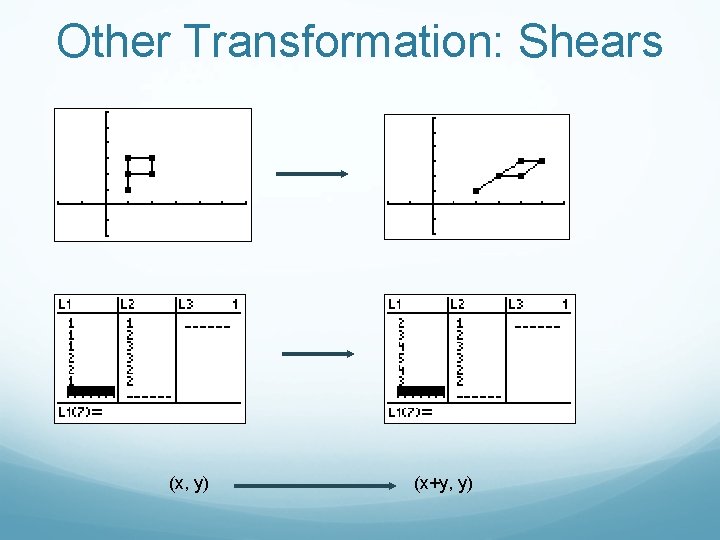
Other Transformation: Shears (x, y) (x+y, y)

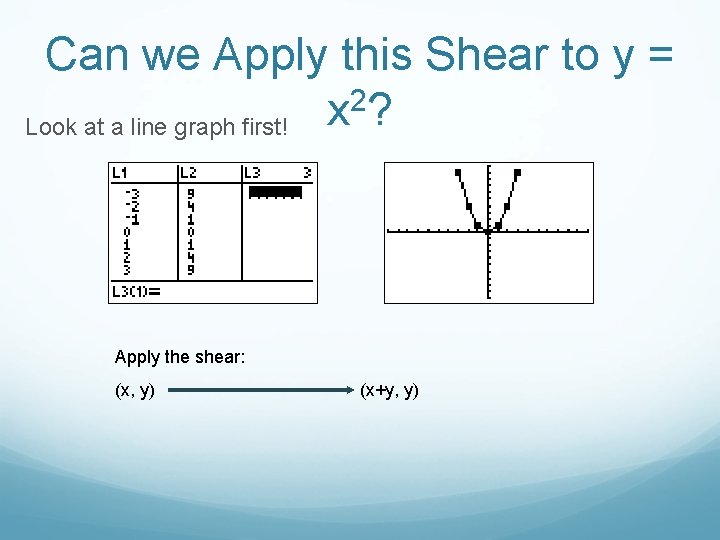
Can we Apply this Shear to y = 2 x? Look at a line graph first! Apply the shear: (x, y) (x+y, y)

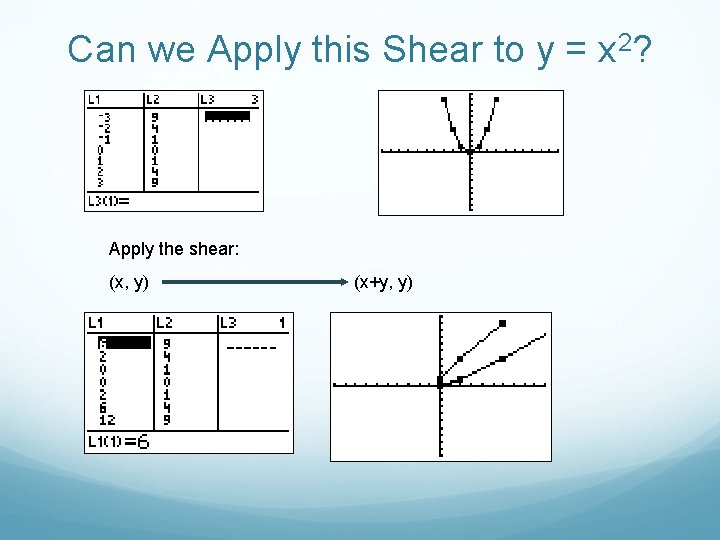
Can we Apply this Shear to y = x 2? Apply the shear: (x, y) (x+y, y)

Can we Apply this Shear to y = x 2? Apply the shear: (x, y) (x+y, y)

Yes we CAN Apply this Shear to y = Apply the shear: x 2. (x, y) (x+y, y) BUT…Can we write the symbolic equation in terms of x and y?

Shear. Apply Example the shear: (x, y) (x+y, y) Parametrically we have: x = t + t 2 Our job is to eliminate t. y = t 2 We will use the substitution method. Now substitute t back into the x equation and we have. to y = x 2

Shears Horizontal Shear for k a constant (x, y ) (x+ky, y) Vertical Shear for k a constant (x, y ) (x, kx+y)

Other Linear Transformations? Rotations

Questions?
 Which two graphs are graphs of polynomial functions?
Which two graphs are graphs of polynomial functions? Hueso esponjoso
Hueso esponjoso Pubis hueso
Pubis hueso Fractura de maisonneuve mecanismo
Fractura de maisonneuve mecanismo Triangulo de scarpa
Triangulo de scarpa Anatomie pied droit
Anatomie pied droit Squelette de la jambe
Squelette de la jambe Horizontal asymptote
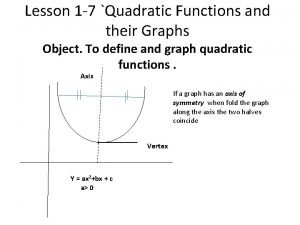
Horizontal asymptote Quadratic functions and their graphs
Quadratic functions and their graphs Vertical answer
Vertical answer Chapter 1 functions and their graphs
Chapter 1 functions and their graphs Sketch the graph of the following rational function
Sketch the graph of the following rational function Common functions and their graphs
Common functions and their graphs Types of polynomials
Types of polynomials Polynomial functions and their graphs
Polynomial functions and their graphs Analyzing graphs of polynomial functions calculator
Analyzing graphs of polynomial functions calculator Exponential functions and their graphs
Exponential functions and their graphs Chapter 2 functions and their graphs answers
Chapter 2 functions and their graphs answers Irrational parent function
Irrational parent function Lesson 3 rational functions and their graphs
Lesson 3 rational functions and their graphs Practice a investigating graphs of polynomial functions
Practice a investigating graphs of polynomial functions Investigating graphs of polynomial functions
Investigating graphs of polynomial functions Personality and its transformations
Personality and its transformations Good and bad state graphs
Good and bad state graphs Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive Translating quadratic functions
Translating quadratic functions Gcse transformations of graphs
Gcse transformations of graphs Transformations of graphs gcse
Transformations of graphs gcse Exponential graphs transformations
Exponential graphs transformations Lesson 2 session 3
Lesson 2 session 3 Comparing distance/time graphs to speed/time graphs
Comparing distance/time graphs to speed/time graphs 7 parent functions
7 parent functions 2-7 parent functions and transformations answer key
2-7 parent functions and transformations answer key Transformations of absolute value functions
Transformations of absolute value functions Sine cosine partner
Sine cosine partner 2-7 parent functions and transformations
2-7 parent functions and transformations 4-1 quadratic functions and transformations
4-1 quadratic functions and transformations Transformations of sine and cosine functions
Transformations of sine and cosine functions Parent functions and transformations
Parent functions and transformations 9-1 quadratic graphs and their properties
9-1 quadratic graphs and their properties Expander graphs and their applications
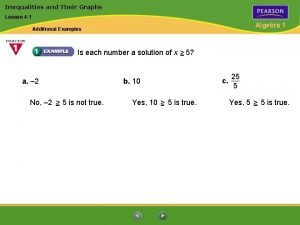
Expander graphs and their applications Lesson 3-1 inequalities and their solutions
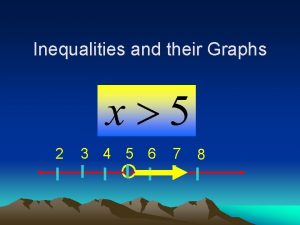
Lesson 3-1 inequalities and their solutions Inequalities and their graphs 3-1
Inequalities and their graphs 3-1 3-1 inequalities and their graphs answer key
3-1 inequalities and their graphs answer key Inequalities and their graphs
Inequalities and their graphs 1-2 analyzing graphs of functions and relations
1-2 analyzing graphs of functions and relations Algebra graphs and functions
Algebra graphs and functions Revenue function graph
Revenue function graph Analyzing graphs of functions
Analyzing graphs of functions Analyzing functions and graphs
Analyzing functions and graphs 2-7 absolute value functions and graphs
2-7 absolute value functions and graphs Rational function properties
Rational function properties Chapter 2 functions and graphs
Chapter 2 functions and graphs Chapter 1 graphs functions and models answers
Chapter 1 graphs functions and models answers Chapter 2 functions and graphs
Chapter 2 functions and graphs Intercept form
Intercept form Parent rational function
Parent rational function Exponential equations examples
Exponential equations examples Lesson 6-4 transforming linear functions answer key
Lesson 6-4 transforming linear functions answer key Transformation of functions
Transformation of functions Dilation of quadratic function
Dilation of quadratic function Transformations of functions
Transformations of functions Transformation of quadratic functions calculator
Transformation of quadratic functions calculator Exponential graph transformations
Exponential graph transformations Transformations polynomial functions
Transformations polynomial functions Using transformations to graph quadratic functions
Using transformations to graph quadratic functions Transformations of periodic functions
Transformations of periodic functions Transformations of linear functions
Transformations of linear functions Transformations of tangent functions
Transformations of tangent functions Vertical answer
Vertical answer 8-3 graphing quadratic functions
8-3 graphing quadratic functions 1-2 lesson quiz transformations of functions
1-2 lesson quiz transformations of functions Using transformations to graph quadratic functions
Using transformations to graph quadratic functions Using transformations to graph quadratic functions
Using transformations to graph quadratic functions Transforming polynomial functions
Transforming polynomial functions Using transformations to graph quadratic functions
Using transformations to graph quadratic functions Bb.4 transformations of quadratic functions
Bb.4 transformations of quadratic functions Function of minerals
Function of minerals Vitamins functions
Vitamins functions Sohcahtoa choshacao
Sohcahtoa choshacao