Exponential Functions Definition of the Exponential Function The










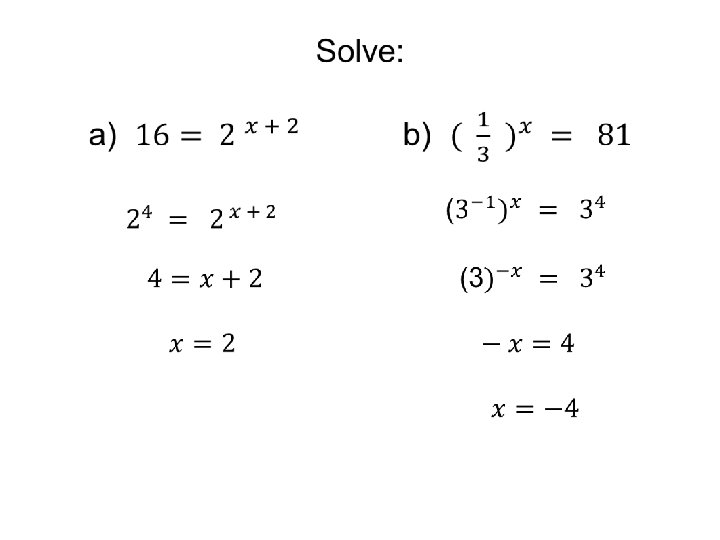


- Slides: 16

Exponential Functions

Definition of the Exponential Function The exponential function f with base b is defined by f (x) = bx or y = bx Where b is a positive constant other than 1 and x is any real number. Here are some examples of exponential functions. f (x) = 2 x Base is 2. g(x) = 10 x Base is 10. h(x) = 3 x+1 Base is 3.

Example The exponential function f (x) = 13. 49(0. 967)x – 1 describes the number of O-rings expected to fail, when the temperature is x°F. On the morning the Challenger was launched, the temperature was 31°F, colder than any previous experience. Find the number of Orings expected to fail at this temperature. Solution. Because the temperature was 31°F, substitute 31 for x and evaluate the function at 31. f (x) = 13. 49(0. 967)x – 1 f (31) = 13. 49(0. 967)31 – 1=3. 77 This is the given function. Substitute 31 for x.

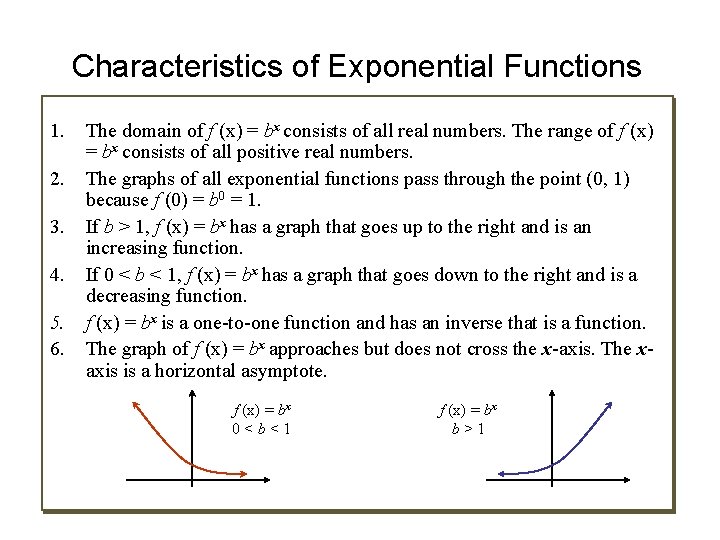
Characteristics of Exponential Functions 1. 2. 3. 4. 5. 6. The domain of f (x) = bx consists of all real numbers. The range of f (x) = bx consists of all positive real numbers. The graphs of all exponential functions pass through the point (0, 1) because f (0) = b 0 = 1. If b > 1, f (x) = bx has a graph that goes up to the right and is an increasing function. If 0 < b < 1, f (x) = bx has a graph that goes down to the right and is a decreasing function. f (x) = bx is a one-to-one function and has an inverse that is a function. The graph of f (x) = bx approaches but does not cross the x-axis. The xaxis is a horizontal asymptote. f (x) = bx 0<b<1 f (x) = bx b>1

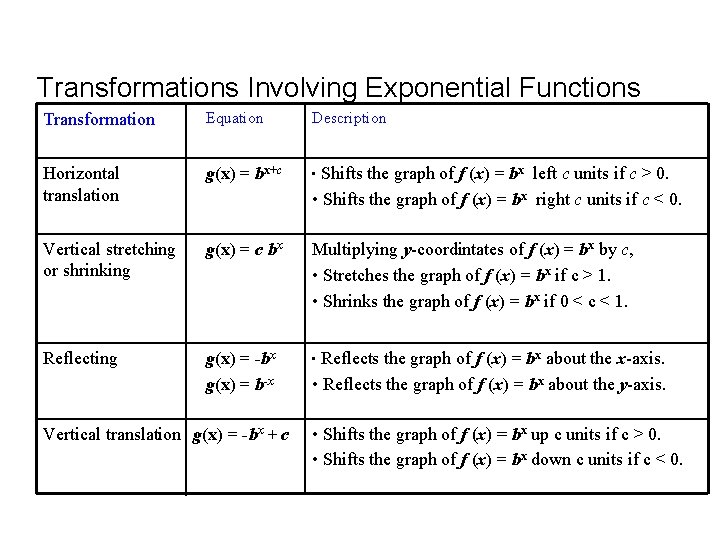
Transformations Involving Exponential Functions Transformation Equation Description Horizontal translation g(x) = bx+c • Shifts Vertical stretching or shrinking g(x) = c bx Multiplying y-coordintates of f (x) = bx by c, • Stretches the graph of f (x) = bx if c > 1. • Shrinks the graph of f (x) = bx if 0 < c < 1. Reflecting g(x) = -bx g(x) = b-x • Reflects Vertical translation g(x) = -bx + c the graph of f (x) = bx left c units if c > 0. • Shifts the graph of f (x) = bx right c units if c < 0. the graph of f (x) = bx about the x-axis. • Reflects the graph of f (x) = bx about the y-axis. • Shifts the graph of f (x) = bx up c units if c > 0. • Shifts the graph of f (x) = bx down c units if c < 0.

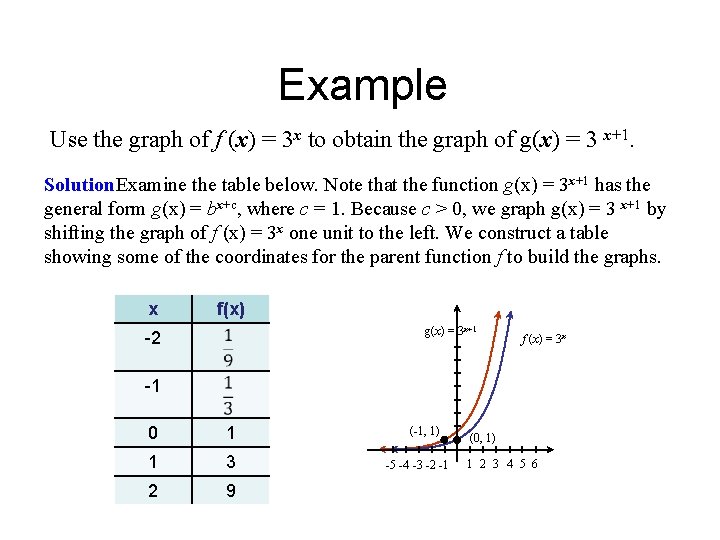
Example Use the graph of f (x) = 3 x to obtain the graph of g(x) = 3 x+1. Solution. Examine the table below. Note that the function g(x) = 3 x+1 has the general form g(x) = bx+c, where c = 1. Because c > 0, we graph g(x) = 3 x+1 by shifting the graph of f (x) = 3 x one unit to the left. We construct a table showing some of the coordinates for the parent function f to build the graphs. x f(x) g(x) = 3 x+1 -2 f (x) = 3 x -1 0 1 1 3 2 9 (-1, 1) -5 -4 -3 -2 -1 (0, 1) 1 2 3 4 5 6

Problems Sketch a graph using transformation of the following: 1. 2. 3. Recall the order of shifting: horizontal, reflection (horz. , vert. ), vertical.

The Natural Base e f (x) = 3 x f (x) = ex 4 (1, 3) f (x) = 2 x 3 (1, e) 2 (1, 2) (0, 1) -1 1

Formulas for Compound Interest •

Example: Choosing Between Investments You want to invest $8000 for 6 years, and you have a choice between two accounts. The first pays 7% per year, compounded monthly. The second pays 6. 85% per year, compounded continuously. Which is the better investment? Solution. The better investment is the one with the greater balance in the account after 6 years. Let’s begin with the account with monthly compounding. We use the compound interest model with P = 8000, r = 7% = 0. 07, n = 12 (monthly compounding, means 12 compoundings per year), and t = 6. The balance in this account after 6 years is $12, 160. 84. more

Example: Choosing Between Investments You want to invest $8000 for 6 years, and you have a choice between two accounts. The first pays 7% per year, compounded monthly. The second pays 6. 85% per year, compounded continuously. Which is the better investment? Solution. For the second investment option, we use the model for continuous compounding with P = 8000, r = 6. 85% = 0. 0685, and t = 6. The balance in this account after 6 years is $12, 066. 60, slightly less than the previous amount. Thus, the better investment is the 7% monthly compounding option.

Example Use A= Pert to solve the following problem: Find the accumulated value of an investment of $2000 for 8 years at an interest rate of 7% if the money is compounded continuously Solution: A= Pert A = 2000 e(. 07)(8) A = 2000 e(. 56) A = $3501. 35

One-to-One Property of Exponential Functions To solve these equations, 1 st Rewrite each side with the same base 2 nd Set the exponents equal to each other 3 rd Solve the equation for the variable
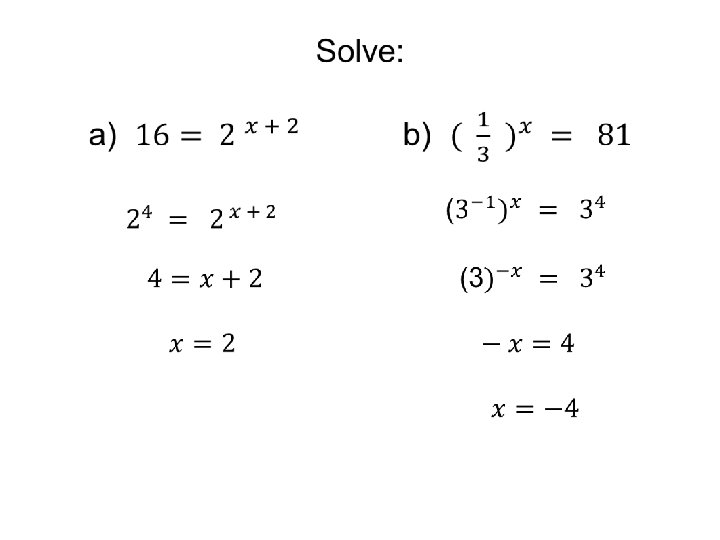

Half-Life b) Determine the quantity present after 1000 years.

 Exponential parent function
Exponential parent function Reverse exponential graph
Reverse exponential graph Composite fx
Composite fx Concepts of exponential functions
Concepts of exponential functions Description of exponential function
Description of exponential function Example of constant ratio
Example of constant ratio Unit 8 review logarithms
Unit 8 review logarithms All real numbers graph
All real numbers graph Exponential and logarithmic functions unit test
Exponential and logarithmic functions unit test Exponential equations examples
Exponential equations examples Is quadratic exponential
Is quadratic exponential Recursive vs explicit rule
Recursive vs explicit rule Practice 8-8 exponential growth and decay
Practice 8-8 exponential growth and decay Domain exponential function
Domain exponential function 6-2 lesson quiz exponential functions
6-2 lesson quiz exponential functions B1oooo
B1oooo Exponential function transformations calculator
Exponential function transformations calculator