Chapter 6 TRANSFORMATIONS OF FUNCTIONS AND THEIR GRAPHS

Chapter 6 TRANSFORMATIONS OF FUNCTIONS AND THEIR GRAPHS Section 6. 1 Shifts, Reflections, and Symmetry Section 6. 2 Vertical Stretches and Compressions Section 6. 3 Horizontal Stretches and Combinations of Transformations Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 1

6. 1 SHIFTS, REFLECTIONS, AND SYMMETRY Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 2

Vertical Shift If g(x) is a function and k is a positive constant, then the graph of • y = g(x) + k is the graph of y = g(x) shifted vertically upward by k units. • y = g(x) − k is the graph of y = g(x) shifted vertically downward by k units. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 3

Horizontal Shift If g(x) is a function and k is a positive constant, then the graph of • y = g(x + k) is the graph of y = g(x) shifted horizontally to the left by k units. • y = g(x − k) is the graph of y = g(x) shifted horizontally to the right by k units. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 4

Inside Versus Outside Changes Translations of a function f(x) can be expressed in the form y = f(x − h) + k. • Outside change by a constant k shifts the graph up by k units if k > 0 (down if k < 0) • Inside change by a constant h shifts the graph right by h units if h > 0 (left if h < 0) Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 5

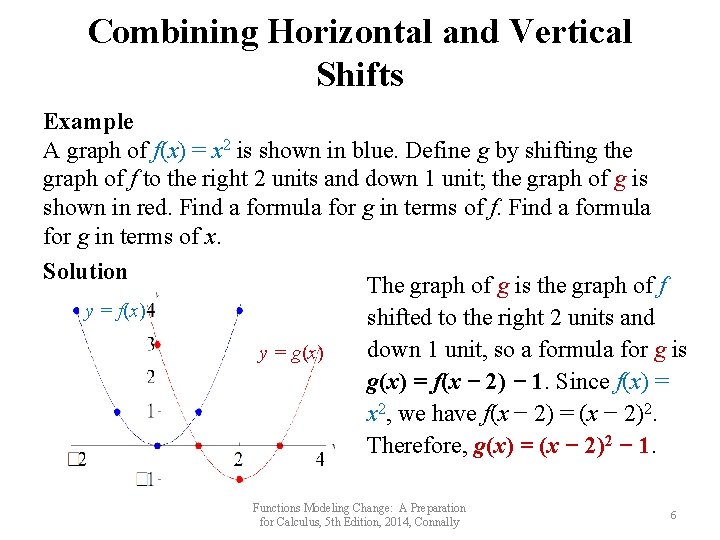
Combining Horizontal and Vertical Shifts Example A graph of f(x) = x 2 is shown in blue. Define g by shifting the graph of f to the right 2 units and down 1 unit; the graph of g is shown in red. Find a formula for g in terms of f. Find a formula for g in terms of x. Solution The graph of g is the graph of f y = f(x) shifted to the right 2 units and down 1 unit, so a formula for g is y = g(x) = f(x − 2) − 1. Since f(x) = x 2, we have f(x − 2) = (x − 2)2. Therefore, g(x) = (x − 2)2 − 1. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 6

A Formula for a Reflection For a function f: • The graph of y = −f(x) is a reflection of the graph of y = f(x) about the x-axis. • The graph of y = f(−x) is a reflection of the graph of y = f(x) about the y-axis. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 7

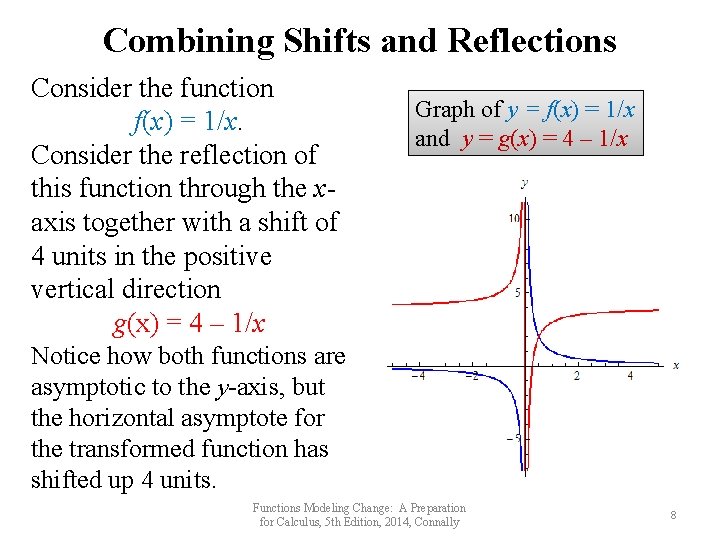
Combining Shifts and Reflections Consider the function f(x) = 1/x. Consider the reflection of this function through the xaxis together with a shift of 4 units in the positive vertical direction g(x) = 4 – 1/x Graph of y = f(x) = 1/x and y = g(x) = 4 – 1/x Notice how both functions are asymptotic to the y-axis, but the horizontal asymptote for the transformed function has shifted up 4 units. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 8

Even Functions Are Symmetric About the y-Axis If f is a function, then f is called an even function if, for all values of x in the domain of f, f(−x) = f(x). The graph of f is symmetric about the y-axis. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 9

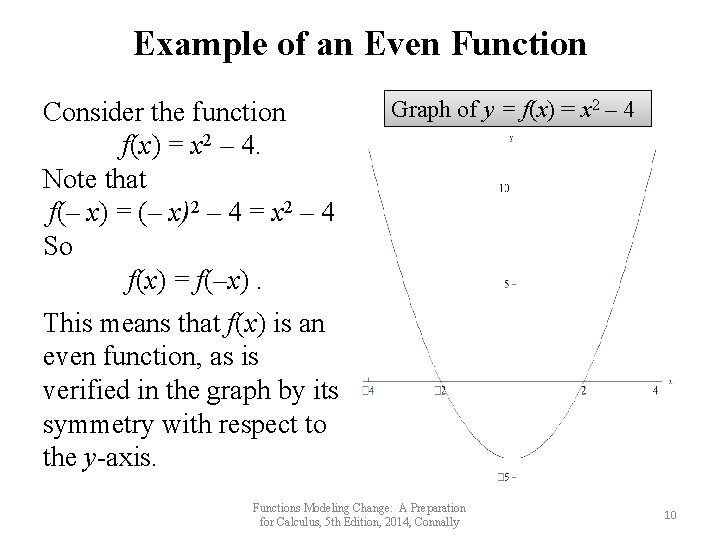
Example of an Even Function Consider the function f(x) = x 2 – 4. Note that f(– x) = (– x)2 – 4 = x 2 – 4 So f(x) = f(–x). Graph of y = f(x) = x 2 – 4 This means that f(x) is an even function, as is verified in the graph by its symmetry with respect to the y-axis. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 10

Odd Functions Are Symmetric About the Origin If f is a function, then f is called an odd function if, for all values of x in the domain of f, f(−x) = − f(x). The graph of f is symmetric about the origin. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 11

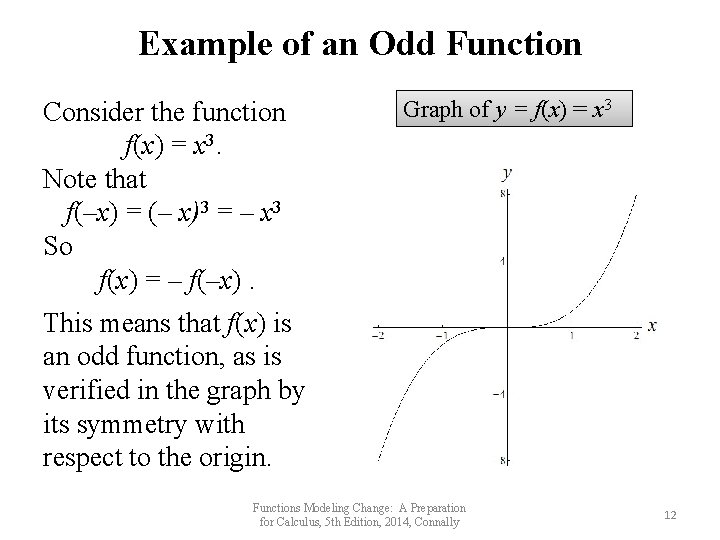
Example of an Odd Function Consider the function f(x) = x 3. Note that f(–x) = (– x)3 = – x 3 So f(x) = – f(–x). Graph of y = f(x) = x 3 This means that f(x) is an odd function, as is verified in the graph by its symmetry with respect to the origin. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 12

6. 2 VERTICAL STRETCHES AND COMPRESSIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 13

Formula for Vertical Stretch or Compression If f is a function and k is a constant, then the graph of y = k ∙ f(x) is the graph of y = f(x) • Vertically stretched by a factor of k, if k > 1. • Vertically compressed by a factor of k, if 0 < k < 1. • Vertically stretched or compressed by a factor |k| and reflected across x-axis, if k < 0. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 14

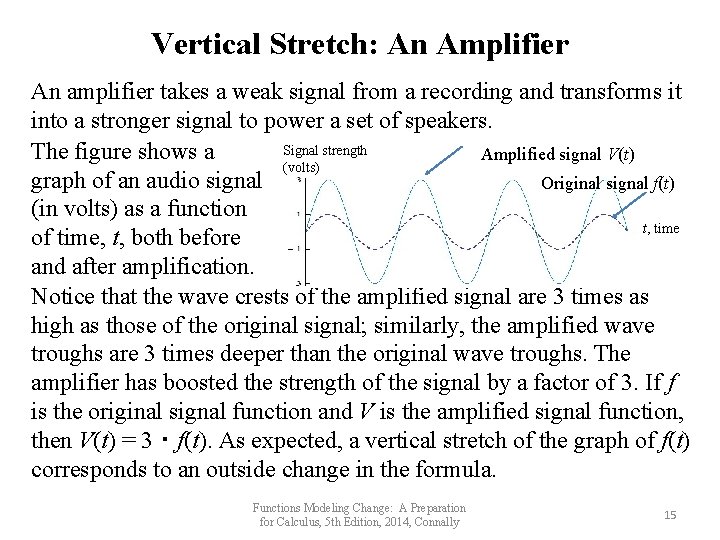
Vertical Stretch: An Amplifier An amplifier takes a weak signal from a recording and transforms it into a stronger signal to power a set of speakers. Signal strength The figure shows a Amplified signal V(t) (volts) graph of an audio signal Original signal f(t) (in volts) as a function t, time of time, t, both before and after amplification. Notice that the wave crests of the amplified signal are 3 times as high as those of the original signal; similarly, the amplified wave troughs are 3 times deeper than the original wave troughs. The amplifier has boosted the strength of the signal by a factor of 3. If f is the original signal function and V is the amplified signal function, then V(t) = 3・f(t). As expected, a vertical stretch of the graph of f(t) corresponds to an outside change in the formula. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 15

Negative Stretch Factor The Figure gives a graph of a function y = f(x), together with a graph of y =− 2 · f(x) and the intermediate transformation y =2 · f(x). The stretch factor is k = − 2. We think of y = − 2 f(x) as a combination of two separate transformations of y = f(x). First, the graph is stretched by a factor of 2, then it is reflected across the x-axis. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 16

Stretch Factors and Average Rates of Change If g(x) = k · f(x), then on any interval, the average rate of change of g equals k · (Average rate of change of f). Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 17

Stretch Factors and Average Rates of Change Example The function s(t) gives the distance (miles) in terms of time (hours). If the average rate of change of s(t) on 0 ≤ t ≤ 4 is 70 mph, what is the average rate of change of ½ s(t) on this interval? Solution The average rate of change of ½ s(t) on the interval 0 ≤ t ≤ 4 is ½ the average rate of change of s(t) on that interval, so it is ½ of 70 or 35 mph. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 18

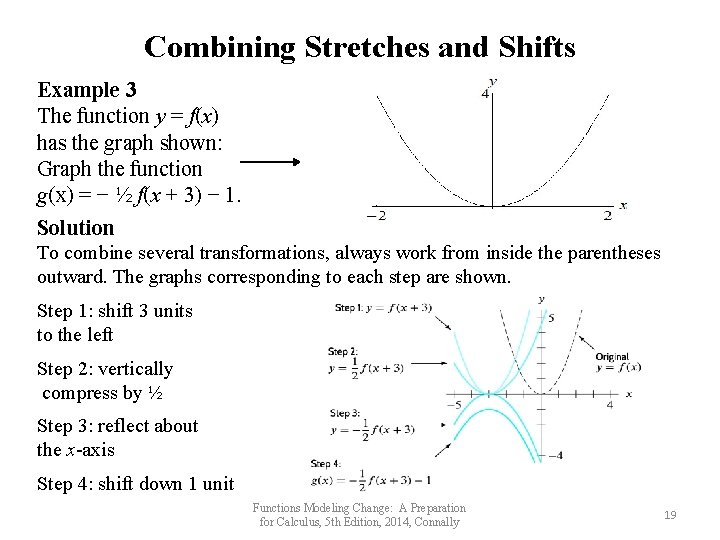
Combining Stretches and Shifts Example 3 The function y = f(x) has the graph shown: Graph the function g(x) = − ½ f(x + 3) − 1. Solution To combine several transformations, always work from inside the parentheses outward. The graphs corresponding to each step are shown. Step 1: shift 3 units to the left Step 2: vertically compress by ½ Step 3: reflect about the x-axis Step 4: shift down 1 unit Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 19

6. 3 HORIZONTAL STRETCHES AND COMBINATIONS OF TRANSFORMATIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 20

Formula for Horizontal Stretch or Compression If f is a function and k a positive constant, then the graph of y = f(k∙x) is the graph of y = f(x) • Horizontally compressed by a factor of 1/k if k > 1, • Horizontally stretched by a factor of 1/k if k < 1. • Horizontally stretched or compressed by a factor 1/|k| and reflected across y-axis, if k < 0. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 21

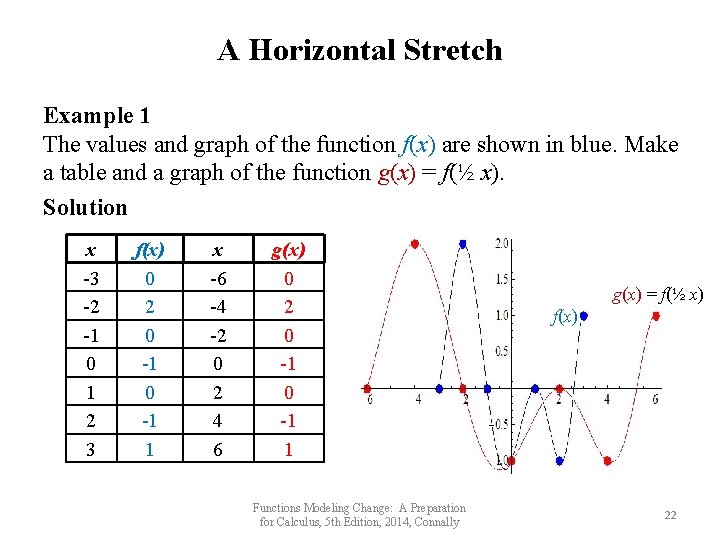
A Horizontal Stretch Example 1 The values and graph of the function f(x) are shown in blue. Make a table and a graph of the function g(x) = f(½ x). Solution x -3 -2 -1 0 1 2 3 f(x) 0 2 0 -1 1 x -6 -4 -2 0 2 4 6 g(x) 0 2 0 -1 1 Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally g(x) = f(½ x) f(x) 22

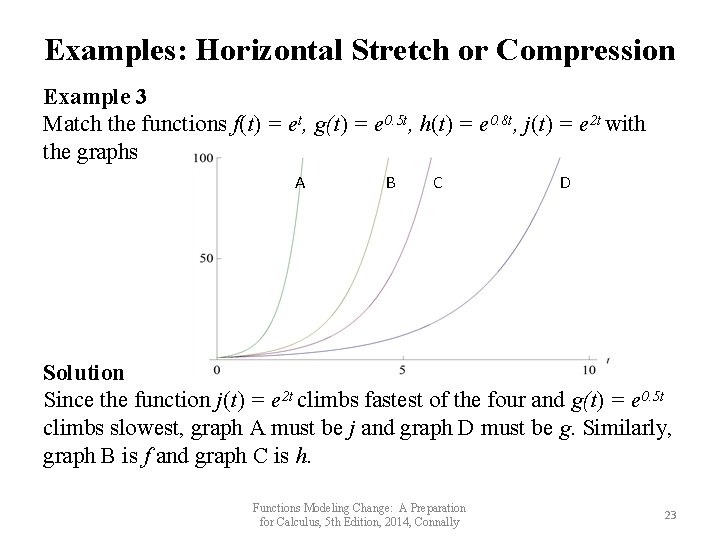
Examples: Horizontal Stretch or Compression Example 3 Match the functions f(t) = et, g(t) = e 0. 5 t, h(t) = e 0. 8 t, j(t) = e 2 t with the graphs A B C D Solution Since the function j(t) = e 2 t climbs fastest of the four and g(t) = e 0. 5 t climbs slowest, graph A must be j and graph D must be g. Similarly, graph B is f and graph C is h. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 23

Multiple Inside Changes Example (a) Rewrite the function y = f (2 x − 6) in the form y = f (B(x − h)). (b) Use the result to describe the graph of y = f (2 x − 6) as the result of first applying a horizontal stretch or compression to the graph of f and then applying a horizontal shift. What is the stretch/compression factor? What is the shift? Solution (a) We have f (2 x − 6) = f (2(x − 3)). (b) Thus, the graph of y = f (2 x − 6) can be obtained from the graph of y = f (x) by first horizontally compressing it by a factor of ½ and then shifting horizontally right by h = 3 units. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 24

Ordering Horizontal and Vertical Transformations For nonzero constants A, B, h and k, the graph of the function y = A f (B (x − h)) + k is obtained by applying the transformations to the graph of f(x) in the following order: • Horizontal stretch/compression by a factor of 1/|B| • Horizontal shift by h units • Vertical stretch/compression by a factor of |A| • Vertical shift by k units If A < 0, follow the vertical stretch/compression by a reflection about the x-axis. If B < 0, follow the horizontal stretch/compression by a reflection about the y-axis. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 25

Multiple Transformations Example 4 (a) Let y = 5(x + 2)2 + 7. Determine the values of A, B, h, and k when y is put in the form y = A f (B(x − h)) + k with f(x) = x 2. List the transformations applied to f(x) = x 2 to give y = 5(x + 2)2 + 7. (b) Sketch a graph of y = 5(x + 2)2 + 7, labeling the vertex. Solution (b) (a) If f(x) = x 2, we see y = 5(x + 2)2 + 7 = 5 f(x + 2) + 7, so A = 5, B = 1, h = − 2, and k = 7. Based on the values of these constants, we carry out these steps: • Horizontal shift 2 to the left of the graph of f(x) = x 2. • Vertical stretch of the resulting graph by a factor of 5. • Vertical shift of the resulting graph up by 7. Since B = 1, there is no horizontal compression, stretch, or reflection. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 26