THE DEFINITE INTEGRAL RECTANGULAR APPROXIMATION RIEMANN SUM AND














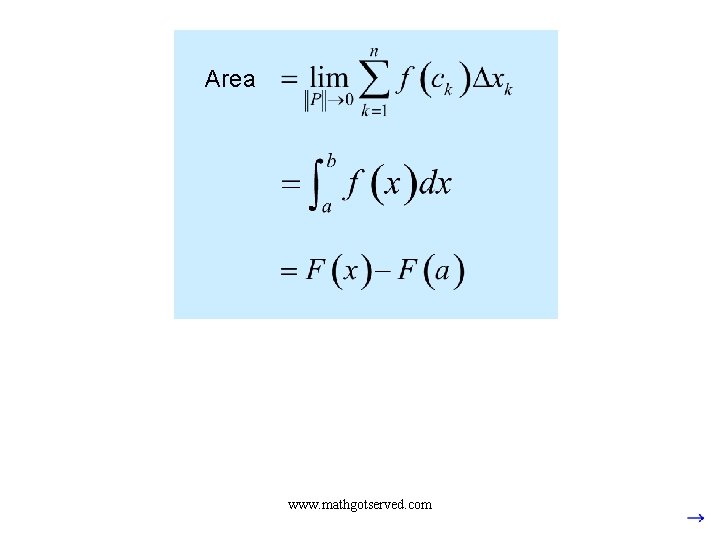

- Slides: 28

THE DEFINITE INTEGRAL RECTANGULAR APPROXIMATION, RIEMANN SUM, AND INTEGRTION RULES

Consider an object moving at a constant rate of 3 ft/sec. Since rate. time = distance: If we draw a graph of the velocity, the distance that the object travels is equal to the area under the line. After 4 seconds, the object has gone 12 feet. velocity time

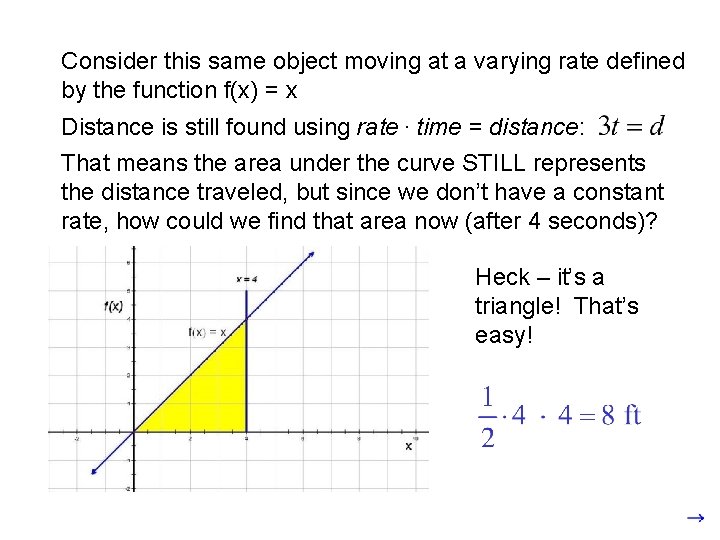
Consider this same object moving at a varying rate defined by the function f(x) = x Distance is still found using rate. time = distance: That means the area under the curve STILL represents the distance traveled, but since we don’t have a constant rate, how could we find that area now (after 4 seconds)? Heck – it’s a triangle! That’s easy!

What happens, though, if the velocity function is not constant, nor does it form a regular geometric shape (with an easy area formula) when we shade the area underneath it? What’s a student to do? ? How can we find the area under that kind of curve? ? Example:

VIDEO TUTORIAL INITIATE SLIDE TO VIEW Links to videos--> Definite Integral Limit of Riemann Sum Geometry I CU 5 L 1 a LRAM MRAM Rectangular Approximations left hand riemann calculus right CU 5 L 1 b pt II LRAM MRAM Rectangular Approximations Left right hand riemann calculus CU 5 L 1 c pt III LRAM MRAM Rectangular Approximations hand Riemann left right calculus CU 5 L 3 Rules for Definite Integrals CU 5 l 4 Using Antiderivatives to Find Definite Integrals CU 5 l 5 fundamental theorem of calculus I and II Cu 5 l 6 trapezoidal rule approximation calculus I and II www. mathgotserved. com

When we find the area under a curve by adding rectangles, the answer is called a Rieman sum. The width of a rectangle is called a subinterval The entire interval is called the partition Subintervals do not all have to be the same size. www. mathgotserved. com

If the partition is denoted by P, then the length of the longest subinterval is called the norm of P and is denoted by . subinterval partition As gets smaller, the approximation for the area gets better. if P is a partition of the interval www. mathgotserved. com

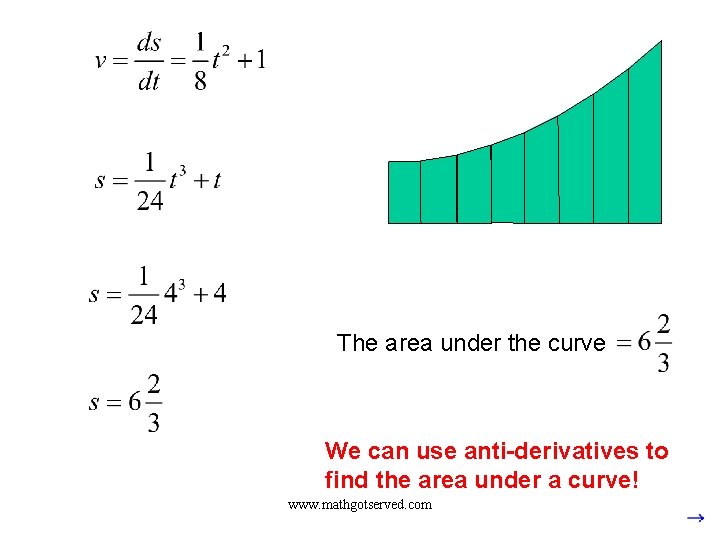
What if: We could split the area under the curve into a lot of thin trapezoids, and each trapezoid would behave like the large one in the previous example. It seems reasonable that the distance will equal the area under the curve. www. mathgotserved. com

The area under the curve We can use anti-derivatives to find the area under a curve! www. mathgotserved. com

is called the definite integral of over . If we use subintervals of equal length, then the length of a subinterval is: The definite integral is then given by: www. mathgotserved. com

Leibnitz introduced a simpler notation for the definite integral: Note that the very small change in x becomes dx. www. mathgotserved. com

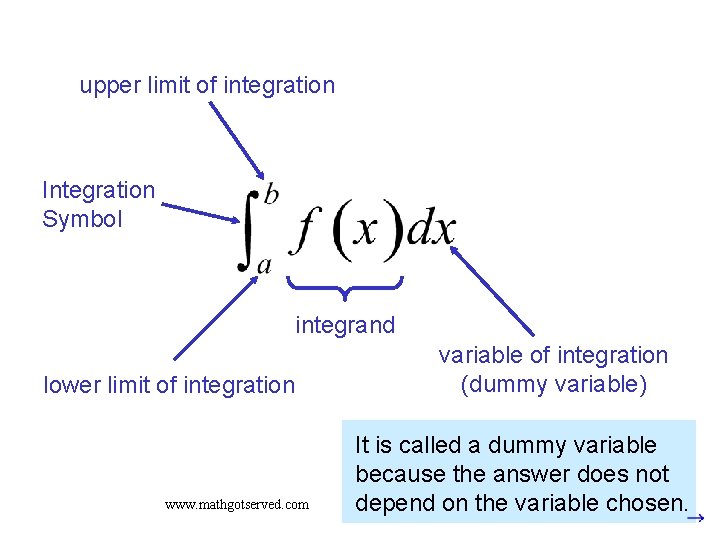
upper limit of integration Integration Symbol integrand lower limit of integration www. mathgotserved. com variable of integration (dummy variable) It is called a dummy variable because the answer does not depend on the variable chosen.

We have the notation for integration, but we still need to learn how to evaluate the integral. www. mathgotserved. com

Rules for definite integrals www. mathgotserved. com

Using the Properties of the Definite Integral Given: www. mathgotserved. com

Riemann Sums There are three types of Riemann Sums Right Riemann: Left Riemann: Midpoint Riemann: www. mathgotserved. com

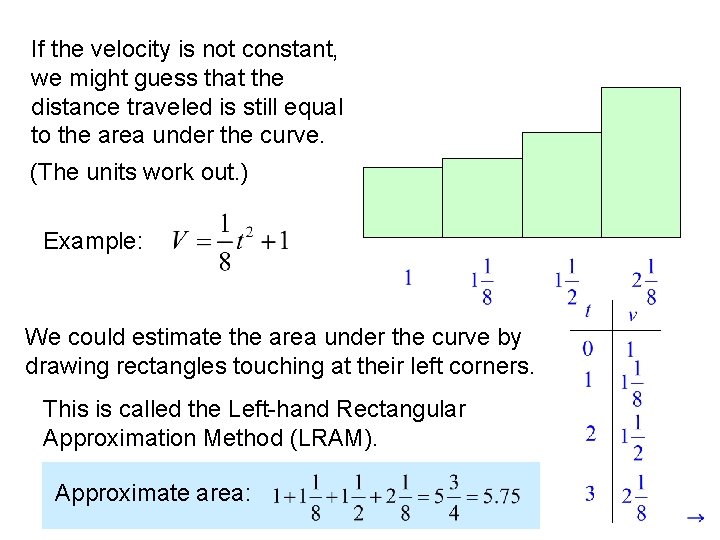
If the velocity is not constant, we might guess that the distance traveled is still equal to the area under the curve. (The units work out. ) Example: We could estimate the area under the curve by drawing rectangles touching at their left corners. This is called the Left-hand Rectangular Approximation Method (LRAM). Approximate area:

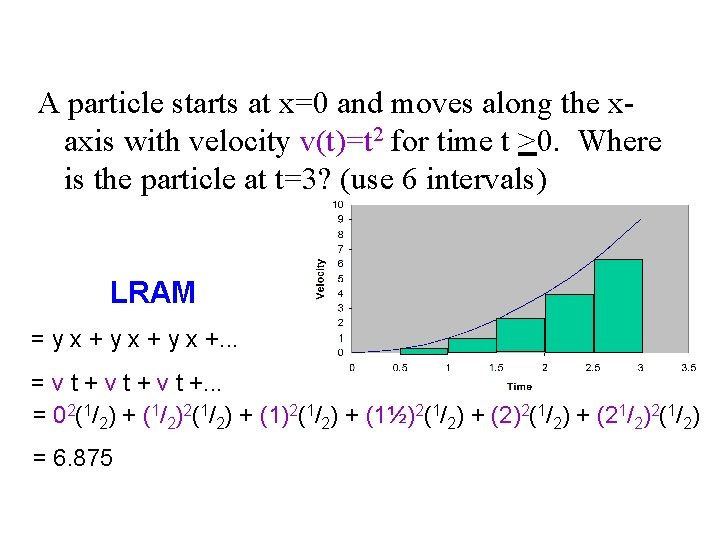
A particle starts at x=0 and moves along the xaxis with velocity v(t)=t 2 for time t >0. Where is the particle at t=3? (use 6 intervals) LRAM = y x +. . . = v t +. . . = 02(1/2) + (1/2)2(1/2) + (1½)2(1/2) + (21/2)2(1/2) = 6. 875

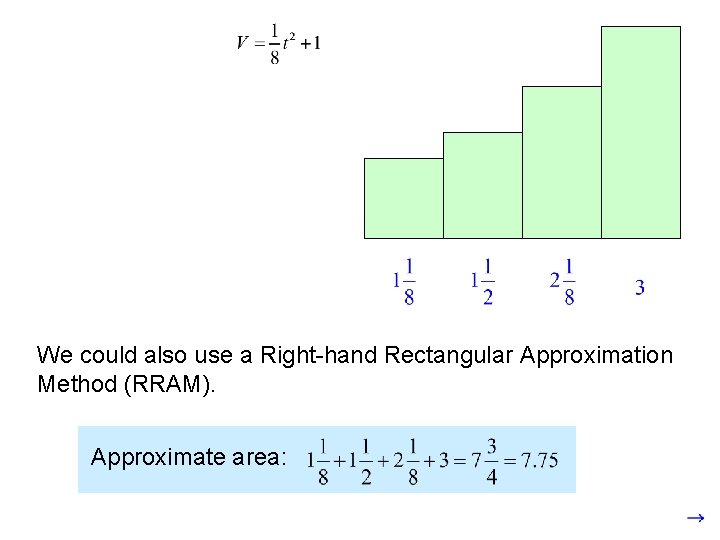
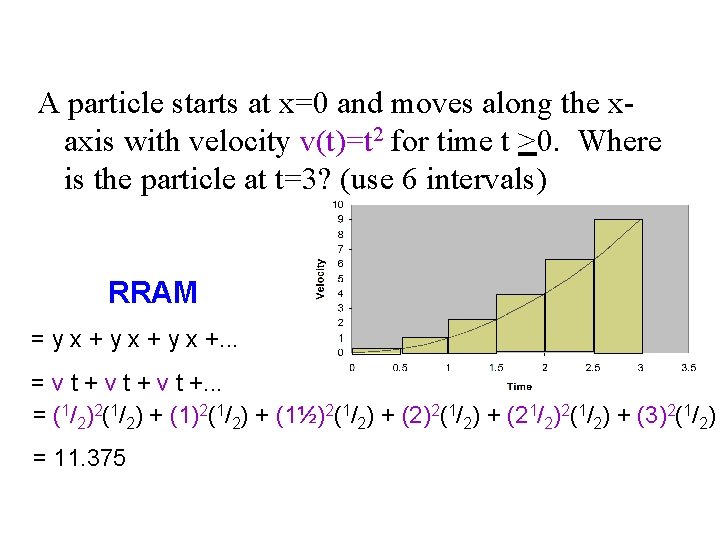
We could also use a Right-hand Rectangular Approximation Method (RRAM). Approximate area:

A particle starts at x=0 and moves along the xaxis with velocity v(t)=t 2 for time t >0. Where is the particle at t=3? (use 6 intervals) RRAM = y x +. . . = v t +. . . = (1/2)2(1/2) + (1½)2(1/2) + (21/2)2(1/2) + (3)2(1/2) = 11. 375

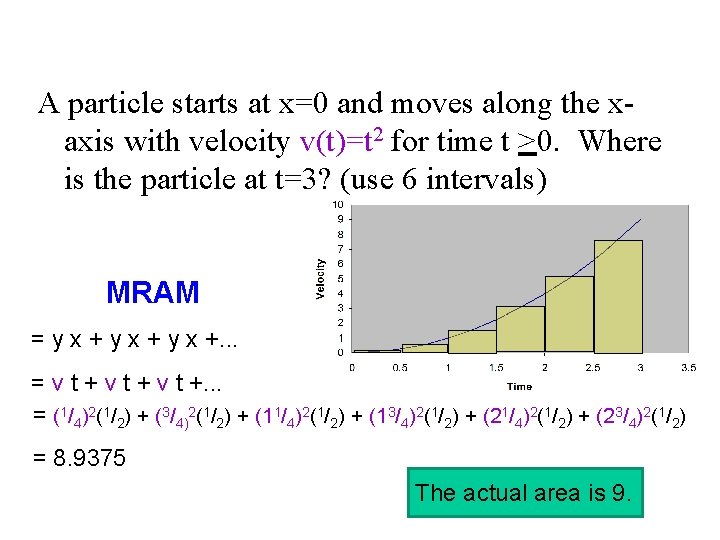
A particle starts at x=0 and moves along the xaxis with velocity v(t)=t 2 for time t >0. Where is the particle at t=3? (use 6 intervals) MRAM = y x +. . . = v t +. . . = (1/4)2(1/2) + (3/4)2(1/2) + (11/4)2(1/2) + (13/4)2(1/2) + (21/4)2(1/2) + (23/4)2(1/2) = 8. 9375 The actual area is 9.

Another approach would be to use rectangles that touch at the midpoint. This is the Midpoint Rectangular Approximation Method (MRAM). In this example there are four subintervals. Approximate area: As the number of subintervals increases, so does the accuracy.

With 8 subintervals: Approximate area: The exact answer for this problem is . width of subinterval

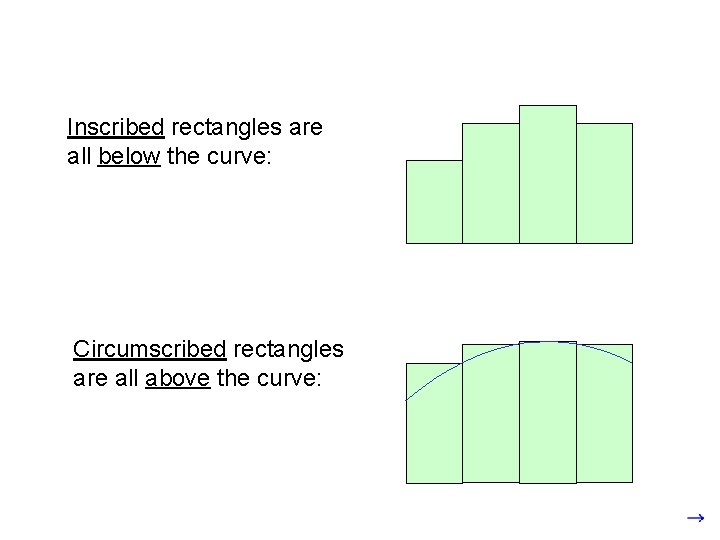
Inscribed rectangles are all below the curve: Circumscribed rectangles are all above the curve:
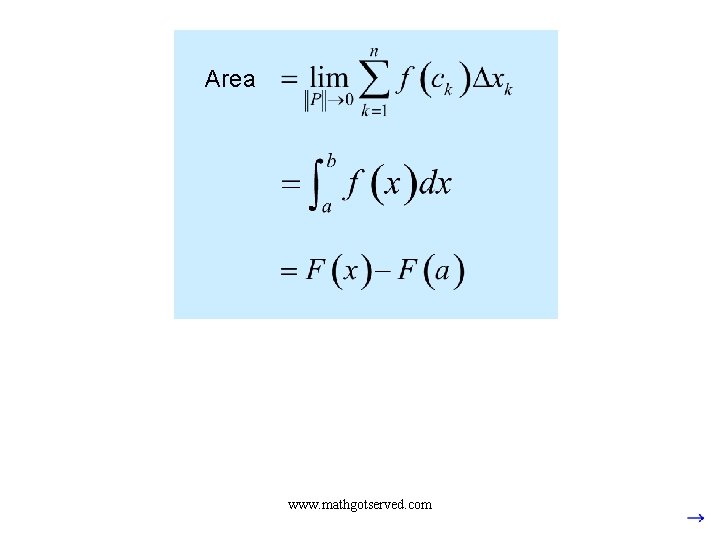
Area www. mathgotserved. com

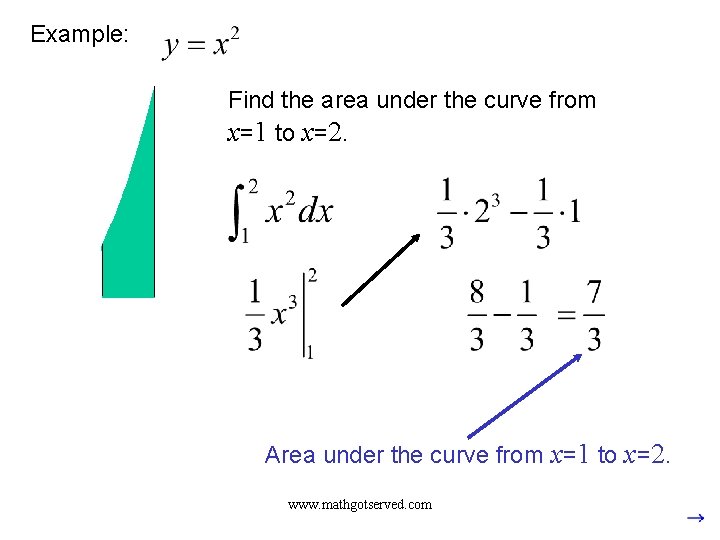
Example: Find the area under the curve from x=1 to x=2. Area from x=0 Area under the curve from x=1 to x=2 to x=1 www. mathgotserved. com

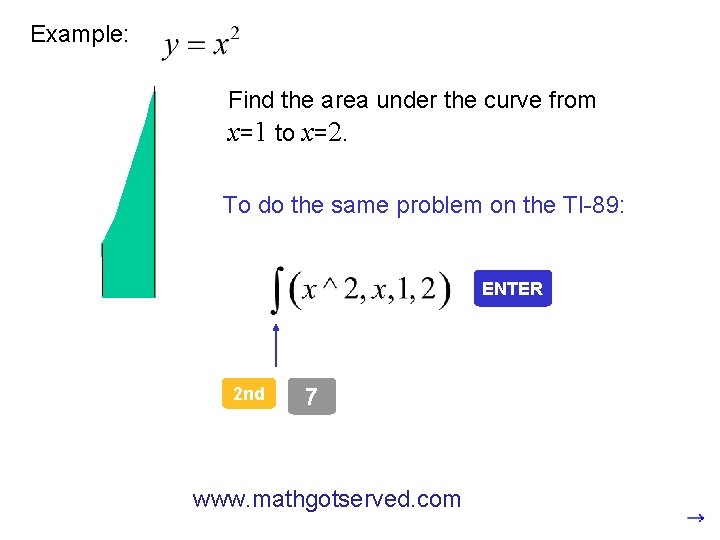
Example: Find the area under the curve from x=1 to x=2. To do the same problem on the TI-89: ENTER 2 nd 7 www. mathgotserved. com

Example: Find the area between the x-axis and the curve from to . pos. neg. On the TI-89: If you use the absolute value function, you don’t need to find the roots. www. mathgotserved. com p
 Riemann sum sigma notation calculator
Riemann sum sigma notation calculator Riemann sum integral
Riemann sum integral Riemann sum to integral
Riemann sum to integral Definite integral vs indefinite integral
Definite integral vs indefinite integral Reimann sum formula
Reimann sum formula Riemann sum symbol
Riemann sum symbol Riemann sum formula
Riemann sum formula Midpoint riemann sum
Midpoint riemann sum Trapazoidal sum
Trapazoidal sum Midpoint riemann formula
Midpoint riemann formula Riemann sum formula
Riemann sum formula Trapezoidal approximation
Trapezoidal approximation Example of definite integral
Example of definite integral Rram formula
Rram formula Definite integral denotes
Definite integral denotes Definite integral integration by parts
Definite integral integration by parts Site:slidetodoc.com
Site:slidetodoc.com Norm of partition
Norm of partition Integral and non integral citation
Integral and non integral citation Integral citation
Integral citation Examples of non integral foreign operations
Examples of non integral foreign operations Integral
Integral S
S Integral lanjutan
Integral lanjutan Int sum(int a int n) int sum=0 i
Int sum(int a int n) int sum=0 i Interpolation vs approximation
Interpolation vs approximation Riemann hypothesis graph
Riemann hypothesis graph Cr equations
Cr equations Georg cantor biografía
Georg cantor biografía