Riemann Sums and the Definite Integral Why Why

Riemann Sums and the Definite Integral

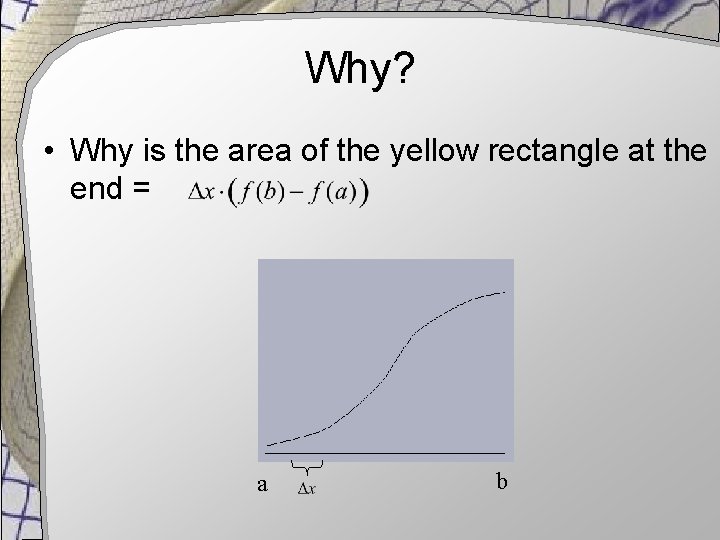
Why? • Why is the area of the yellow rectangle at the end = a b

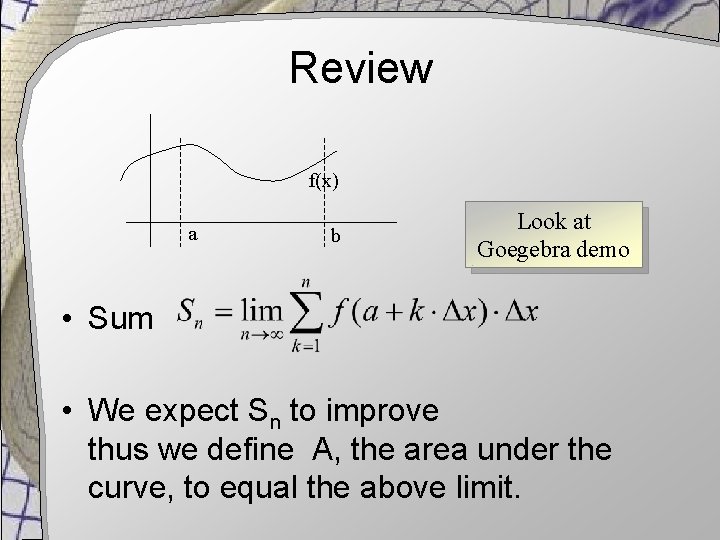
Review f(x) a b • We partition the interval into n sub-intervals • Evaluate f(x) at right endpoints of kth sub-interval for k = 1, 2, 3, … n

Review f(x) a b Look at Goegebra demo • Sum • We expect Sn to improve thus we define A, the area under the curve, to equal the above limit.

Riemann Sum 1. Partition the interval [a, b] into n subintervals a = x 0 < x 1 … < xn-1< xn = b • • • Call this partition P The kth subinterval is xk = xk-1 – xk Largest xk is called the norm, called ||P|| 2. Choose an arbitrary value from each subinterval, call it

Riemann Sum 3. Form the sum This is the Riemann sum associated with • • the function f the given partition P the chosen subinterval representatives We will express a variety of quantities in terms of the Riemann sum

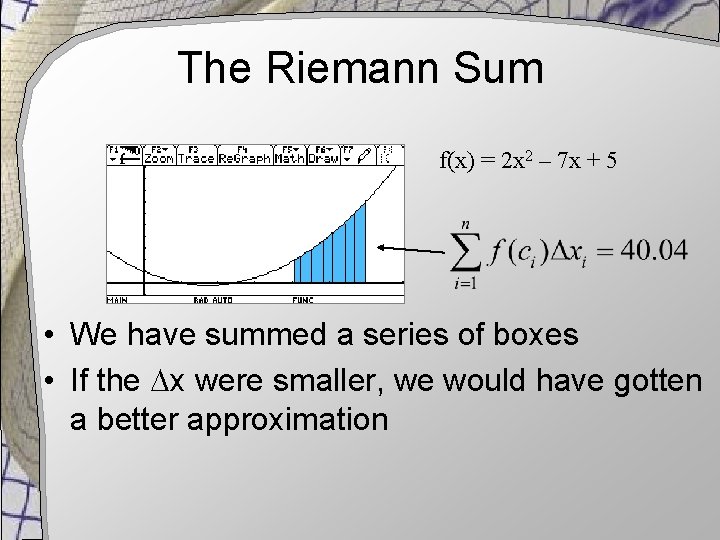
The Riemann Sum Calculated • Consider the function 2 x 2 – 7 x + 5 • Use x = 0. 1 • Let the = left edge of each subinterval • Note the sum

The Riemann Sum f(x) = 2 x 2 – 7 x + 5 • We have summed a series of boxes • If the x were smaller, we would have gotten a better approximation

The Definite Integral • The definite integral is the limit of the Riemann sum • We say that f is integrable when § the number I can be approximated as accurate as needed by making ||P|| sufficiently small § f must exist on [a, b] and the Riemann sum must exist

Example • Try • Use summation on calculator.

Example • Note increased accuracy with smaller x

Limit of the Riemann Sum • The definite integral limit of the Riemann sum. is the

Properties of Definite Integral • Integral of a sum = sum of integrals • Factor out a constant • Dominance

Properties of Definite Integral f(x) • Subdivision rule a b c

Area As An Integral • The area under the curve on the interval [a, b] f(x) A a c

Distance As An Integral • Given that v(t) = the velocity function with respect to time: • Then Distance traveled can be determined by a definite integral • Think of a summation for many small time slices of distance

Assignment • Section 5. 3 • Page 314 • Problems: 3 – 47 odd