5 2 Riemann Sums and Area I Riemann

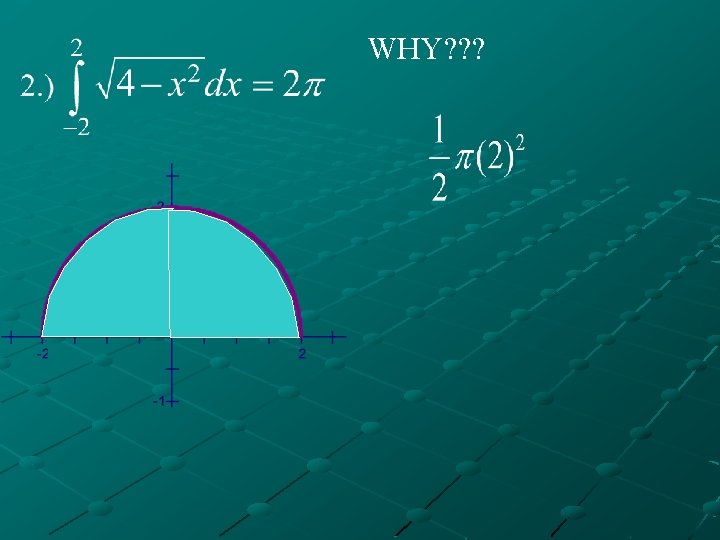
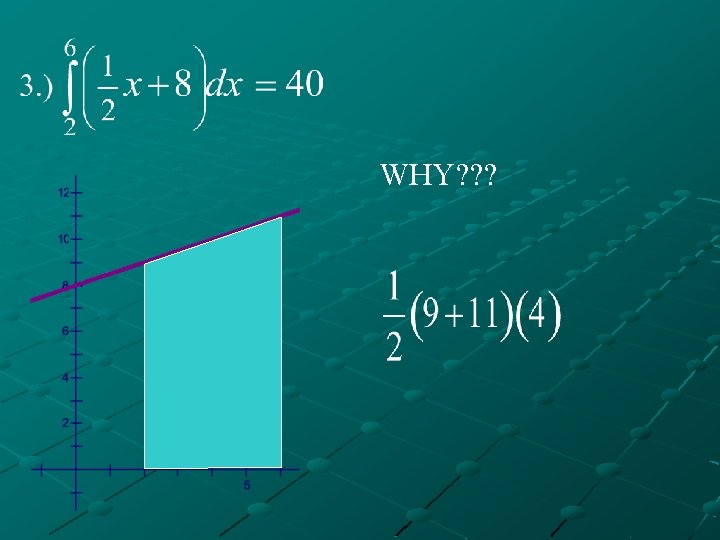
  • Slides: 20
Download presentation
5. 2 Riemann Sums and Area

5. 2 Riemann Sums and Area

I. Riemann Sums A. ) Let f (x) be defined on [a, b]. Partition

I. Riemann Sums A. ) Let f (x) be defined on [a, b]. Partition [a, b] by choosing These partition [a, b] into n parts of length Δx 1, Δx 2, … Δxn. In each subinterval, choose a point c 1, c 2, …cn and form the sum This is called a Riemann Sum *NOTE: LRAM, MRAM, and RRAM are all Riemann sums.

B. ) Def. - The NORM of P, denoted ||P||, is the length of

B. ) Def. - The NORM of P, denoted ||P||, is the length of the largest subinterval. C. ) Def. – If is defined on [a, b], then the DEFINITE INTEGRAL of f (x) over [a, b] is provided the limit exists. This is denoted *NOTE: If the limit exists, then f (x) is said to be integrable on [a, b].

II. EXISTENCE A. ) Thm: (Existence of the limit of a Riemann Sum) 1.

II. EXISTENCE A. ) Thm: (Existence of the limit of a Riemann Sum) 1. ) If f (x) is continuous on [a, b], then f (x) is integrable on [a, b]. 2. ) If f (x) is bounded and has a finite number of discontinuities on [a, b], then f (x) is integrable on [a, b].

III. Examples A. ) Express the limit as a definite integral: , where P

III. Examples A. ) Express the limit as a definite integral: , where P is a partition of [1, 4].

B. ) Express as a limit. where P is a partition of .

B. ) Express as a limit. where P is a partition of .

III. Definite Integrals and Technology A. ) fn. Int – Under MATH – 9

III. Definite Integrals and Technology A. ) fn. Int – Under MATH – 9 where f (x) is the function, x is the variable of integration, and a and b are the bounds of the integration.

B. ) Use your calculator to evaluate the following definite integrals:

B. ) Use your calculator to evaluate the following definite integrals:

V. Area Under a Curve A. ) Def. - If f (x) ≥ 0

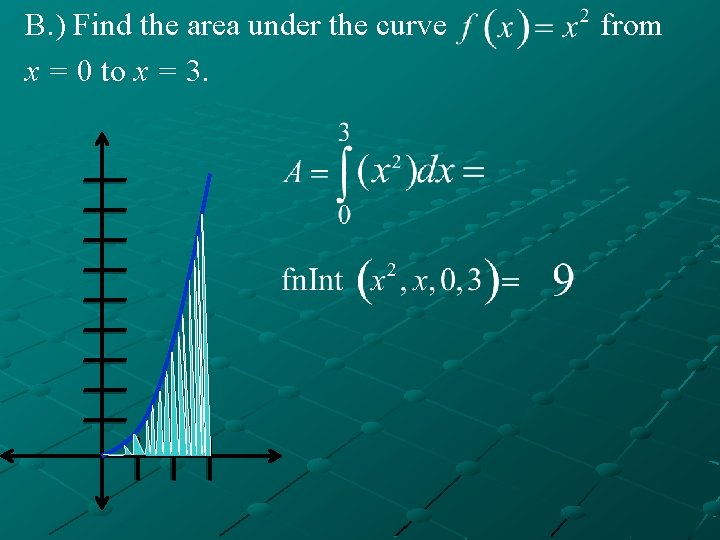
V. Area Under a Curve A. ) Def. - If f (x) ≥ 0 and integrable on [a, b], then the area bounded by the curve, the x-axis, and the vertical lines x = a and x = b is

B. ) Find the area under the curve x = 0 to x =

B. ) Find the area under the curve x = 0 to x = 3. from

C. ) Find the area bounded by the curve the x-axis, and the vertical

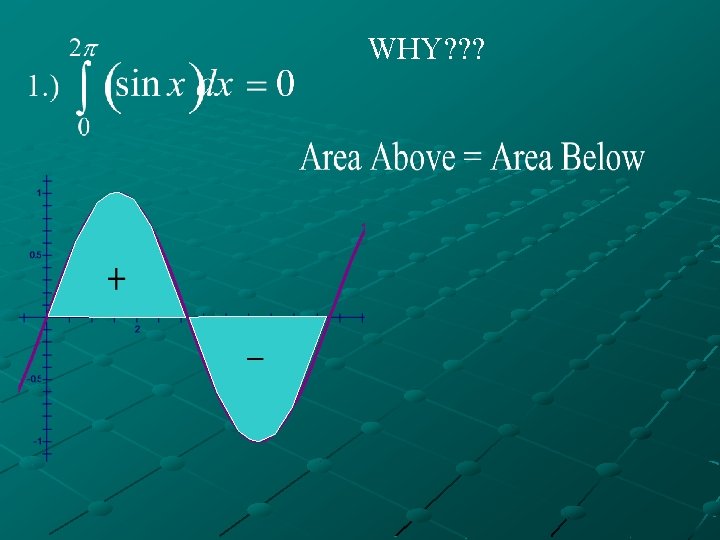
C. ) Find the area bounded by the curve the x-axis, and the vertical lines x = -1 to x = 3. By Geometry By Definite Integral - WHY? ? -

D. ) FACT – For any integrable function: **Note – AREA is ALWAYS POSITIVE,

D. ) FACT – For any integrable function: **Note – AREA is ALWAYS POSITIVE, the definite integral MAY be NEGATIVE.

VI. Examples A. ) Determine the value of the following definite integrals by using

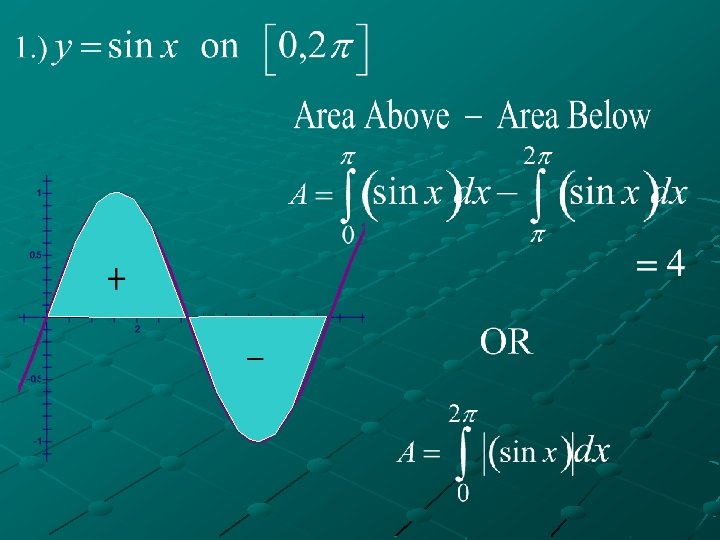
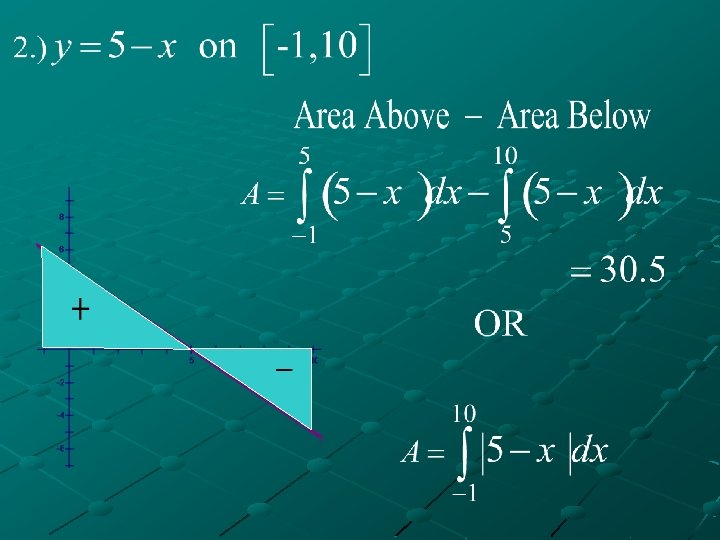
VI. Examples A. ) Determine the value of the following definite integrals by using the areas bounded by the graph of the function, the x-axis, and the bounds given.

WHY? ? ?

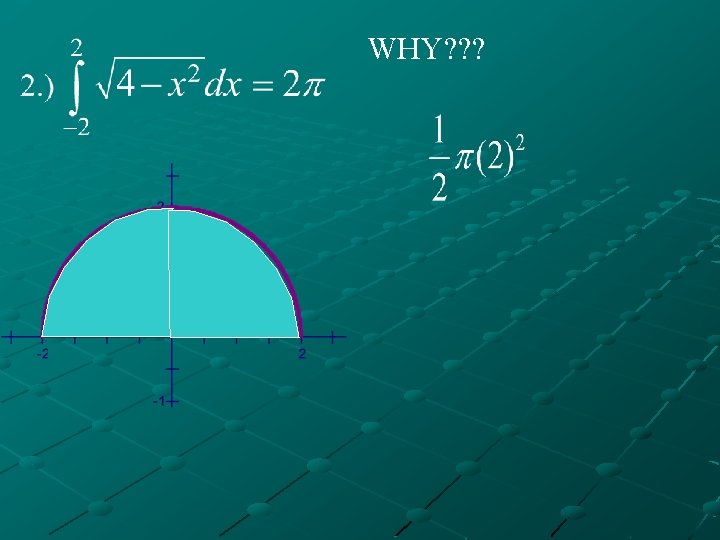
WHY? ? ?

WHY? ? ?

WHY? ? ?

WHY? ? ?

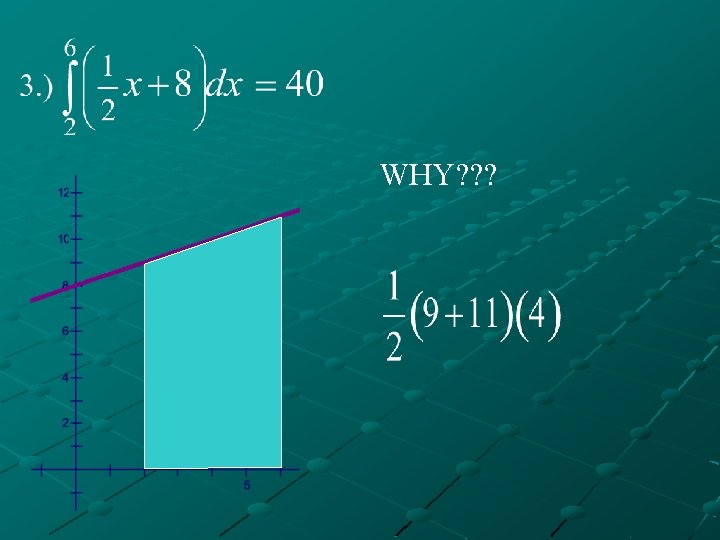
WHY? ? ?

B. ) Express the area bounded by f (x) and the xaxis in terms

B. ) Express the area bounded by f (x) and the xaxis in terms of an integrable expression and then find it.

Riemann Sum Riemann Sum Formula Riemann Sum StepRiemann Sum Riemann Sum Formula Riemann Sum Step
Riemann Sums What is a Riemann Sum TakesRiemann Sums What is a Riemann Sum Takes
4 2 Area 4 3 Riemann Sums and4 2 Area 4 3 Riemann Sums and
Riemann Sums Approximating Area One of the classicalRiemann Sums Approximating Area One of the classical
RIEMANN SUMS THE DEFINITE INTEGRAL INTEGRAL AS AREARIEMANN SUMS THE DEFINITE INTEGRAL INTEGRAL AS AREA
Riemann Sums Approximating Area One of the classicalRiemann Sums Approximating Area One of the classical
Area Riemann Sums Chapter 5 1 Distance TraveledArea Riemann Sums Chapter 5 1 Distance Traveled
Riemann Sums and the Definite Integral Prepared ByRiemann Sums and the Definite Integral Prepared By
4 3 Riemann Sums and Definite Integrals Objectives4 3 Riemann Sums and Definite Integrals Objectives
4 3 Riemann Sums and Definite Integrals 14 3 Riemann Sums and Definite Integrals 1
CHAPTER 4 SECTION 4 3 RIEMANN SUMS ANDCHAPTER 4 SECTION 4 3 RIEMANN SUMS AND
4 3 Riemann Sums and Definite Integrals Objectives4 3 Riemann Sums and Definite Integrals Objectives
Left and RightHand Riemann Sums Rizzi Calc BCLeft and RightHand Riemann Sums Rizzi Calc BC
Definite Integrals Riemann Sums and Trapezoidal Rule WhyDefinite Integrals Riemann Sums and Trapezoidal Rule Why
Riemann Sums and the Definite Integral Lesson 5Riemann Sums and the Definite Integral Lesson 5
Cameron Clary Riemann Sums the Trapezoidal Rule andCameron Clary Riemann Sums the Trapezoidal Rule and
Riemann Sums and the Definite Integral Why WhyRiemann Sums and the Definite Integral Why Why
Section 4 3 Riemann Sums and Definite IntegralsSection 4 3 Riemann Sums and Definite Integrals
RIEMANN SUMS AND DEFINITE INTEGRALS Section 4 3RIEMANN SUMS AND DEFINITE INTEGRALS Section 4 3