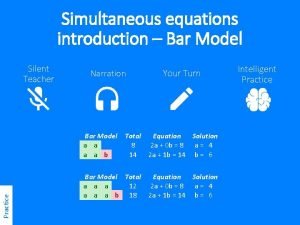
The CauchyRiemann CR Equations Introduction The CauchyRiemann CR

The Cauchy–Riemann (CR) Equations

Introduction • The Cauchy–Riemann (CR) equations is one of the most fundamental in complex function analysis. • This provides analyticity of a complex function. • In real function analysis, analyticity of a function depends on the smoothness of the function on • But for a complex function, this is no longer the case as the limit can be defined many direction

The Cauchy–Riemann (CR) Equations • A complex function can be written as • It is analytic iff the first derivatives and satisfy two CR equations • D

The Cauchy–Riemann (CR) Equations (2)

The Cauchy–Riemann (CR) Equations (3) • Theorem 1 says that If is continuous, then obey CR equations • While theorem 2 states the converse i. e. if are continuous (obey CR equation) then is analytic

Proof of Theorem 1 • D • The may approach the z from all direction • We may choose path I and II, and equate them •

Proof of Theorem 1 (2) • g • ff

Proof of Theorem 1 (3) • F • h

Example

Example (2)

Exponential Function • It is denoted as or exp • It may also be expressed as • The derivatives is

Properties • D • F • G • • D H F d

Example

Trigonometric Function • Using Euler formula Then we obtain trigonometry identity in complex • Furthermore • The derivatives • Euler formula for complex

Trigonometric Function (2) • F • f

Hyperbolic Function • F • Derivatives • Furthermore • Complex trigonometric and hyperbolic function is related by

Logarithm • It is expressed as • The principal argument • Since the argument of • And is multiplication of

Examples

General power • G • f

Examples

Homework • • Problem set 13. 4 1, 2, 4, 10. Problem set 13. 5 no 2, 9, 15. Problem set 13. 6 no 7 & 11. Problem set 13. 7 no 5, 10, 22.