T Madas T Madas A cylinder is shown

A cylinder is shown below. The radius of its base is 6 cm and

A tank without a lid is in the shape of a cylinder. The radius

A can without a lid is in the shape of a cylinder. The radius

Find the volume of this compound shape in terms of π Using Pythagoras Theorem:

Find the volume of this compound shape in terms of π The volume of

Find the volume of this compound shape in terms of π Total volume of

A water can is in the shape of a cuboid with the measurements given

From a cone of height 24 cm and base radius 9 cm, the upper

A conical frustum has a height of 10 cm, base radius 10 cm and

A conical frustum has a height of 15 cm, base radius 12 cm and

A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness

An ice hockey puck can be modelled as a cylinder of radius 4. 2

A tin has a radius of 3. 8 cm and a height of 9.

A cylindrical piece of wood is sawn along its length so that the resulting

A metal ball bearing can be modelled as a sphere of radius 2. 5

One of the two sections of a sand timer can be modelled as a

A sphere with a radius of α cm has the same volume as a

A cylindrical bucket of radius 9 cm contains some water. A metal sphere is

x + 7. 5 A cylinder’s height is 7. 5 cm greater than its

The nut shown below can be modelled as a hexagonal prism with a cylindrical

A cylinder has a height of 12 cm and the radius of its base

Slides: 69

Download presentation

A cylinder is shown below. The radius of its base is 6 cm and has a volume of 1000 cm 3. Calculate its surface area to 3 significant figures. Volume = base area x height 8. 84 cm 6 cm h 1000 = 6 x π x h 1000 ≈ 113. 1 x h h ≈ 1000 ÷ 113. 1 h ≈ 8. 84 cm © T Madas

A cylinder is shown below. The radius of its base is 6 cm and has a volume of 1000 cm 3. Calculate its surface area to 3 significant figures. Surface Area: 6 x π x 2 ≈ 226. 2 cm 2 8. 84 cm 6 cm 2 x 6 x π x 8. 84 ≈ 333. 3 cm 2 559. 5 cm 2 8. 84 cm Circumference of circle 560 cm 2 [ 3 s. f. ] © T Madas

A tank without a lid is in the shape of a cylinder. The radius of its base is 30 cm and has a capacity of 225 litres. Calculate its surface area, to 2 significant figures. 30 cm 79. 6 cm 1 litre = 1000 cm 3 h 225 litres = 225000 cm 3 Volume = base area x height 225000 = 30 x π x h 225000 ≈ 2827 x h h ≈ 225000 ÷ 2827 h ≈ 79. 6 cm © T Madas

A tank without a lid is in the shape of a cylinder. The radius of its base is 30 cm and has a capacity of 225 litres. Calculate its surface area, to 2 significant figures. 30 x π ≈ 2827 cm 2 79. 6 cm 30 cm Surface Area: h 2 x 30 x π x 79. 6 ≈ 15004 cm 2 17831 cm 2 79. 6 cm Circumference of circle 18000 cm 2 [ 2 s. f. ] © T Madas

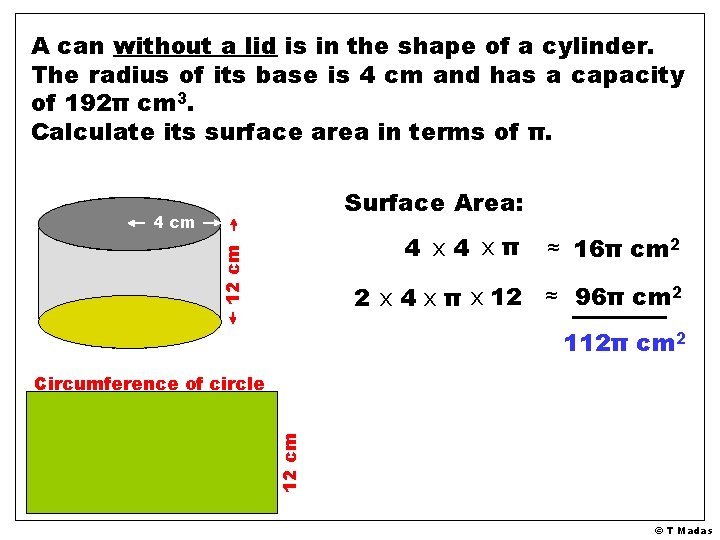
A can without a lid is in the shape of a cylinder. The radius of its base is 4 cm and has a capacity of 192π cm 3. Calculate its surface area in terms of π. Volume = base area x height 12 cm 4 cm h 192π = 4 x π x h 192π = 16π h = 12 cm © T Madas

A can without a lid is in the shape of a cylinder. The radius of its base is 4 cm and has a capacity of 192π cm 3. Calculate its surface area in terms of π. Surface Area: 4 cm 12 cm 4 xπ ≈ 16π cm 2 2 x 4 x π x 12 ≈ 96π cm 2 112π cm 2 12 cm Circumference of circle © T Madas

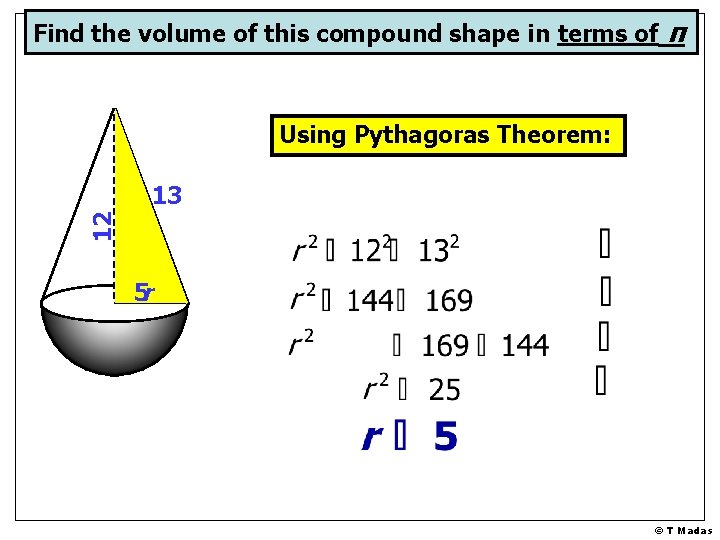
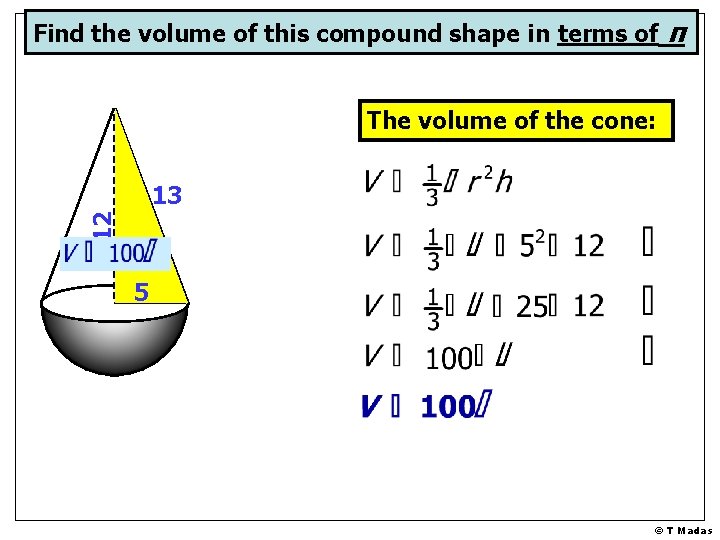
Find the volume of this compound shape in terms of π Using Pythagoras Theorem: 12 13 5 r © T Madas

Find the volume of this compound shape in terms of π The volume of the cone: 12 13 5 © T Madas

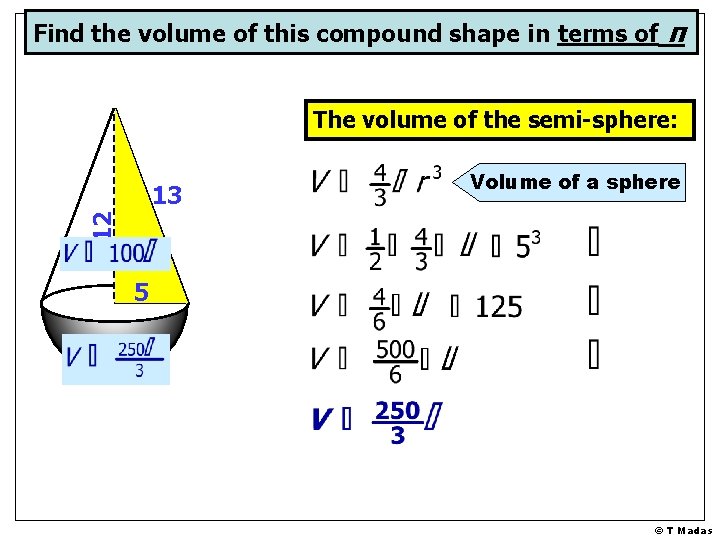
Find the volume of this compound shape in terms of π The volume of the semi-sphere: Volume of a sphere 12 13 5 © T Madas

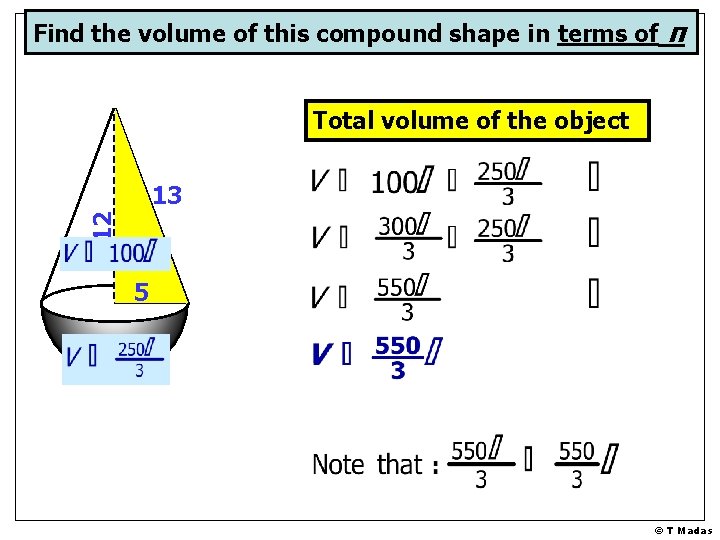
Find the volume of this compound shape in terms of π Total volume of the object 12 13 5 © T Madas

A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? Volume of a cuboid 20 cm length x width x height V = lwh V = 15 x 10 x 20 15 cm 10 cm V = 3000 cm 3 © T Madas

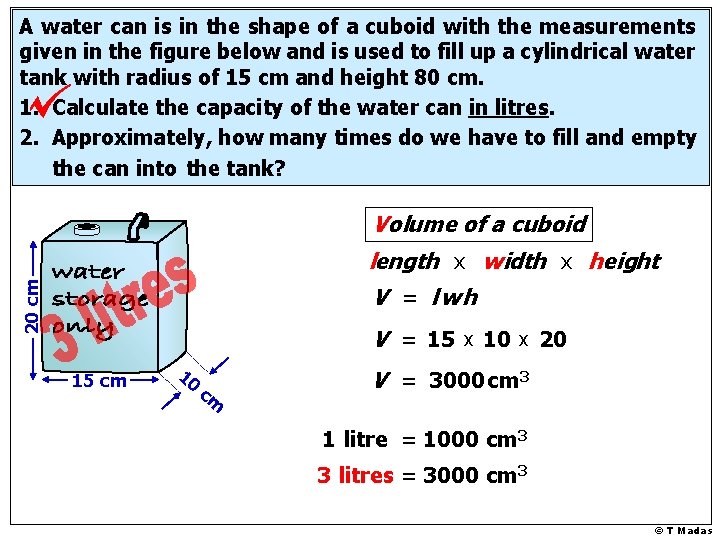
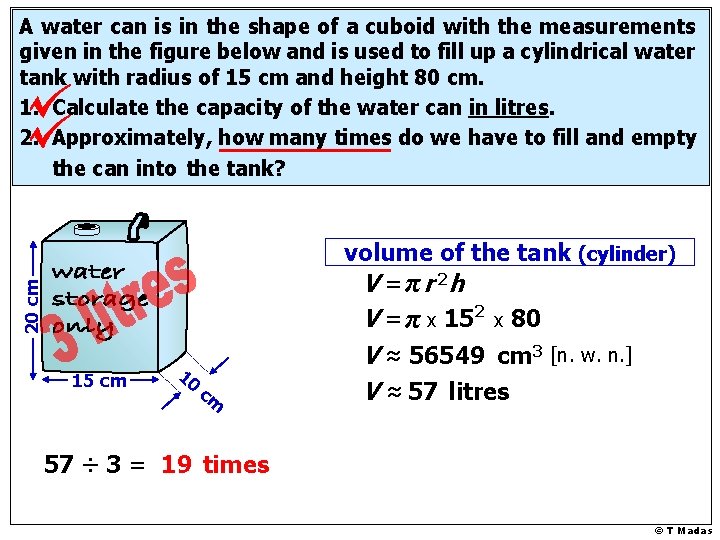
A water can is in the shape of a cuboid with the measurements given in the figure below and is used to fill up a cylindrical water tank with radius of 15 cm and height 80 cm. 1. Calculate the capacity of the water can in litres. 2. Approximately, how many times do we have to fill and empty the can into the tank? 20 cm volume of the tank (cylinder) V = π r 2 h V = π x 152 x 80 15 cm 10 cm V ≈ 56549 cm 3 [n. w. n. ] V ≈ 57 litres 57 ÷ 3 = 19 times © T Madas

From a cone of height 24 cm and base radius 9 cm, the upper part is removed leaving a frustum of height 8 cm and upper base radius 6 cm. Calculate the volume of this frustum correct to 3 s. f. 24 cm Volume of Original Cone Volume of upper Cone (removed part) 8 cm 6 cm Volume of the frustum 9 cm © T Madas

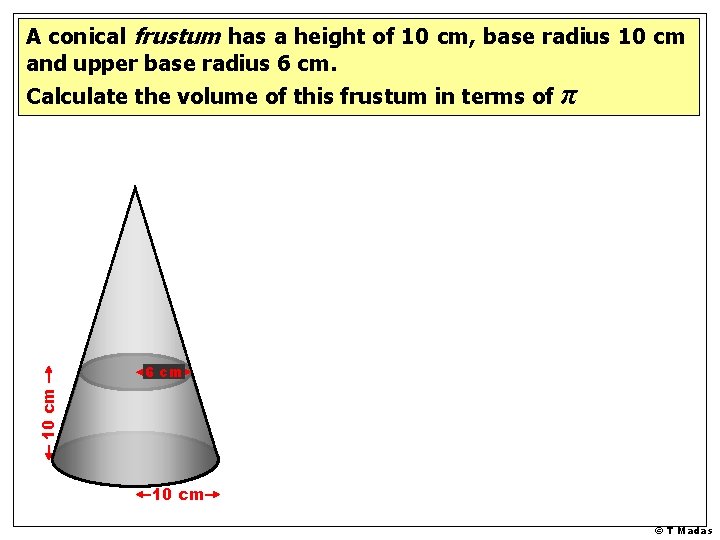
A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 10 cm 6 cm 10 cm © T Madas

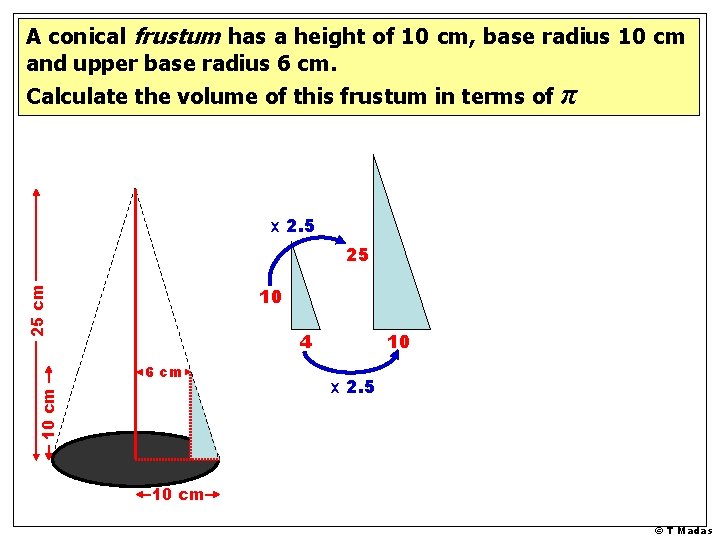
A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π x 2. 5 25 25 cm 10 4 10 cm 6 cm 10 x 2. 5 10 cm © T Madas

A conical frustum has a height of 10 cm, base radius 10 cm and upper base radius 6 cm. Calculate the volume of this frustum in terms of π 25 cm Volume of “Original” Cone Volume of upper Cone (removed part) 10 cm 6 cm Volume of the frustum 10 cm © T Madas

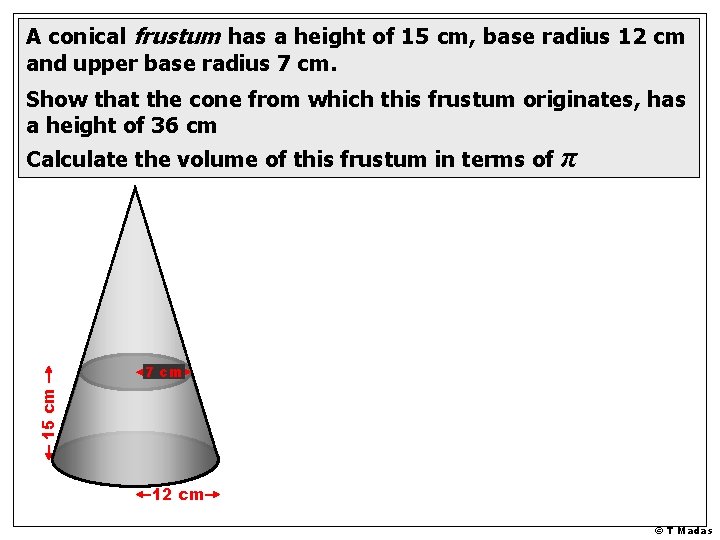
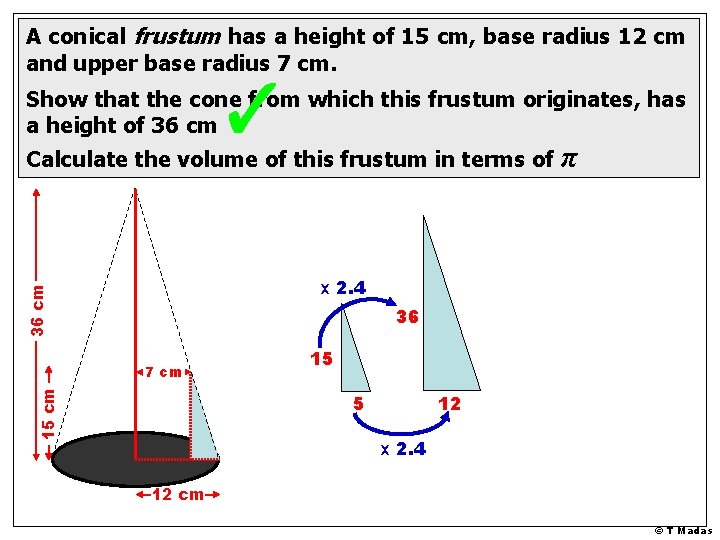
A conical frustum has a height of 15 cm, base radius 12 cm and upper base radius 7 cm. Show that the cone from which this frustum originates, has a height of 36 cm Calculate the volume of this frustum in terms of π 15 cm 7 cm 12 cm © T Madas

A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm V = π r 2 h V = π x 35. 52 x 7. 5 V ≈ 29694 mm 3 V ≈ 29. 7 cm 3 [3 s. f. ] 7 ± 0. 5 mm 1 cm 3 = 1000 mm 3 © T Madas

A digestive biscuit has its diameter measured as 70 ± 1 mm. Its thickness is measured as 7 ± 0. 5 mm. Calculate to 3 significant figures: 1. the maximum possible volume of the biscuit in cm 3. 2. the minimum possible surface area of this biscuit in cm 2. 70 ± 1 mm 7 ± 0. 5 mm A = π r 2 + 2π r h A=π x 34. 52 + 2 x π x 34. 5 x 6. 5 A ≈ 8888 mm 2 V ≈ 88. 9 cm 2 [3 s. f. ] 1 cm 2 = 100 mm 2 © T Madas

Exam Question © T Madas

An ice hockey puck can be modelled as a cylinder of radius 4. 2 cm and a thickness of 3. 2 cm. The puck is made out of rubber material with a density of 1. 35 grams per cm 3. Calculate to 3 significant figures: (a) The volume of the puck in cm 3 (b) The mass of the puck in grams 4. 2 cm 3. 2 cm V = π r 2 h V = π x 4. 22 x 3. 2 V ≈ 177. 337 cm 3 V ≈ 177 cm 3 [3 s. f. ] Density of 1. 35 grams per cm 3 means that there is a mass of 1. 35 grams for every cm 3 of volume: Mass = 177. 337 x 1. 35 ≈ 239. 404 = 239 grams (3 s. f. ) © T Madas

A tin has a radius of 3. 8 cm and a height of 9. 2 cm. A label is stuck all the way round the side of the tin. Calculate the area of the label, giving your answer in cm 2 correct to 3 significant figures. 23. 88 9. 2 3. 8 lengths in cm c c C=2 x πx r C = 2 x π x 3. 8 C ≈ 23. 88 cm The required area is: 23. 88 x 9. 2 = 220 cm 2 [3 s. f. ] © T Madas

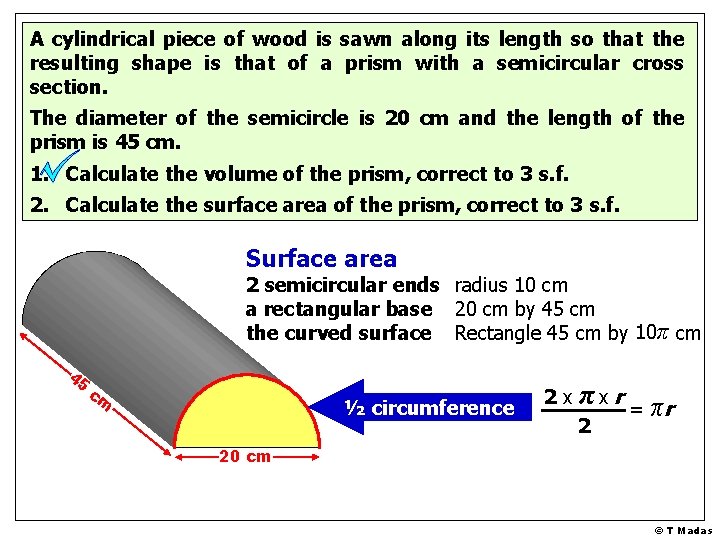
A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. 20 cm V = 50π x 45 c cm V = 2250 π c 45 2 2 π x 10 V= x 45 2 c V= πx r 2 x h c Volume = x - sectional area x length (height) V = 7070 cm 3 [3 s. f. ] © T Madas

A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm the curved surface Rectangle 45 cm by 10? π cm 45 cm ½ circumference 2 x πx r = πr 2 20 cm © T Madas

A cylindrical piece of wood is sawn along its length so that the resulting shape is that of a prism with a semicircular cross section. The diameter of the semicircle is 20 cm and the length of the prism is 45 cm. 1. Calculate the volume of the prism, correct to 3 s. f. 2. Calculate the surface area of the prism, correct to 3 s. f. Surface area 2 semicircular ends radius 10 cm a rectangular base 20 cm by 45 cm the curved surface Rectangle 45 cm by 10? π cm 45 π cm 20 cm x 102 = 100π 20 x 45 = 900 45 x 10π = 450π 900 + 550π 2630 cm 2 [3 s. f. ] © T Madas

A metal ball bearing can be modelled as a sphere of radius 2. 5 cm. The ball bearing is to be melted and remoulded into the shape of a cone with a height of 4. 8 cm. Calculate the radius of the base of the cone, in cm correct to 2 significant figures. volume of the sphere V= 4 3 πr 3 = 4 x 3 π x 2. 53 ≈ 65. 4498 cm 3 volume of the cone 1 3 πr 2 h = 1 x 3 π x r 2 x 4. 8 ≈ 5. 0265 r 2 cm 3 c c 5. 0265 r 2 = 65. 4498 r 2 = 13. 0209 r = 3. 6 cm c V= [2 s. f. ] © T Madas

One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 3 9 4 x 3 3 π x 33 x 18π π x 32 x 9 3 81π 3 Measurements in cm 1 x 3 π x 33 x 3 27π 1 2 volume of a sphere V= 4 3 πr 3 volume of a cylinder V = π r 2 h volume of a cone V= 1 3 πr 2 h © T Madas

One of the two sections of a sand timer can be modelled as a semi sphere connected to a cylinder which is in turn connected to a cone. All three solids share the same axis of symmetry. The radius of these solids is 3 cm and the heights of the cylinder and the cone are 9 cm and 3 cm respectively. Calculate the volume of the sand timer in terms of π. 252π 3 126π 9 4 x 3 3 π x 33 x ≈ 792 cm 3 1 2 18π π x 32 x 9 3 81π 126π Measurements in cm 3 1 x 3 π x 33 x 3 27π © T Madas

A sphere with a radius of α cm has the same volume as a cone with a base radius of α cm. Find the height of the cone, in terms of α. volume of the sphere πα 3 V= πα 3 = 4 3 3 x α 3= 4 3 α= π α 2 h 1 3 h x 3 π α 2 h c 4 3 1 3 c 4 3 c V= volume of the cone 4α = h h = 4α , i. e. the height of the cone is 4 times the base radius © T Madas

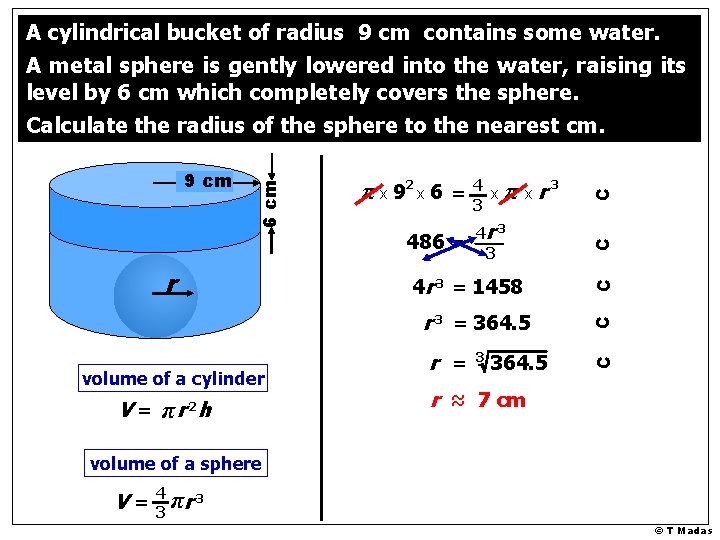
A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. © T Madas

486 = V = π r 2 h 4 r 3 3 4 r 3 = 1458 r 3 = 364. 5 c c volume of a cylinder π x r 3 3 c r 4 x 3 c π x 92 x 6 = c 9 cm 6 cm A cylindrical bucket of radius 9 cm contains some water. A metal sphere is gently lowered into the water, raising its level by 6 cm which completely covers the sphere. Calculate the radius of the sphere to the nearest cm. r = 364. 5 r ≈ 7 cm volume of a sphere V= 4 3 πr 3 © T Madas

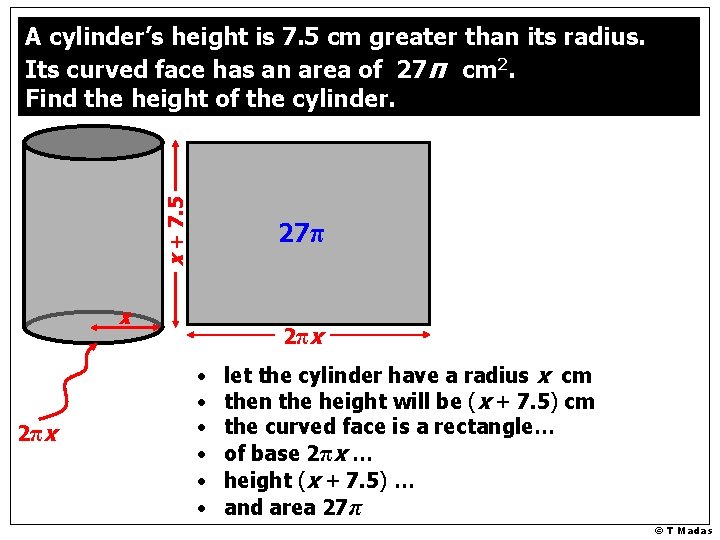
x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 27π x 2π x • • • let the cylinder have a radius x cm then the height will be (x + 7. 5) cm the curved face is a rectangle… of base 2πx … height (x + 7. 5) … and area 27π © T Madas

2πx (x + 7. 5) = 27π c 2 x (x + 7. 5) = 27 c 2π x 2 x 2 + 15 x = 27 c x 27π 2 x 2 + 15 x – 27 = 0 c x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. © T Madas

2πx (x + 7. 5) = 27π c 2 x (x + 7. 5) = 27 c 2 x 2 + 15 x – 27 = 0 c x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. c 2 x (x + 7. 5) = 27 c 2 x 2 + 15 x = 27 c 2π x 2πx (x + 7. 5) = 27π 2 x 2 + 15 x – 27 = 0 c x © T Madas

c 2 x (x + 7. 5) = 27 c 2 x 2 + 15 x – 27 = 0 c x 2πx (x + 7. 5) = 27π 2 x – 3 x + 9 = 0 c x + 7. 5 A cylinder’s height is 7. 5 cm greater than its radius. Its curved face has an area of 27π cm 2. Find the height of the cylinder. 1. 5 cm x= 2π x -9 Therefore the height of the cylinder is 9 cm © T Madas

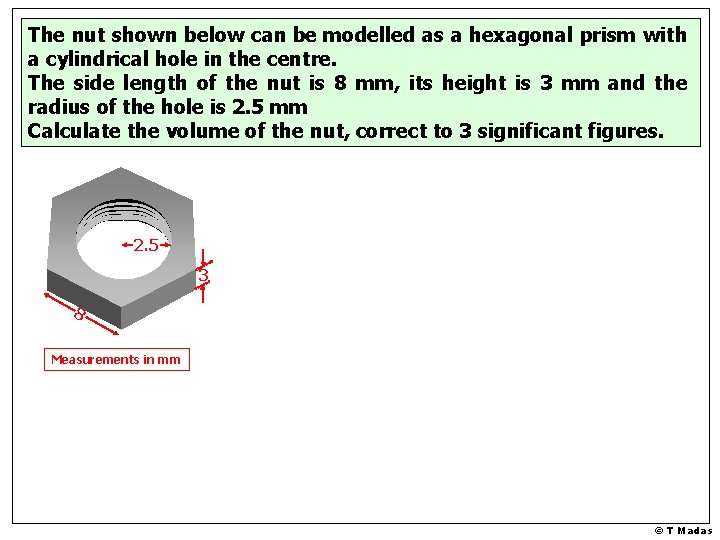
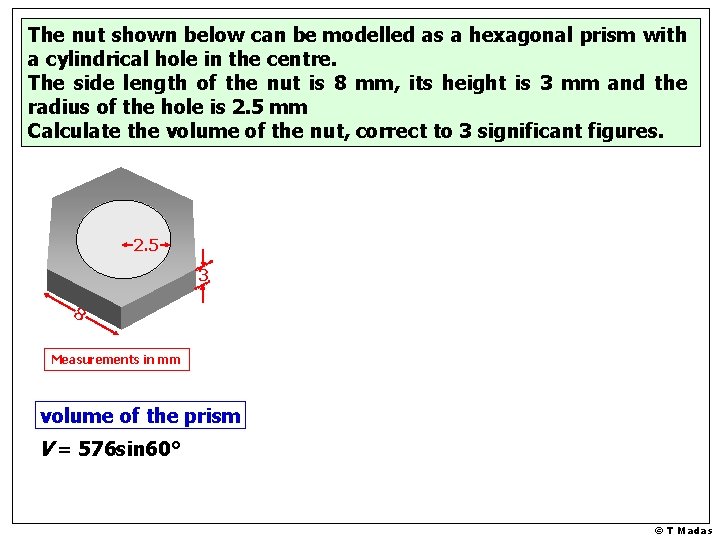
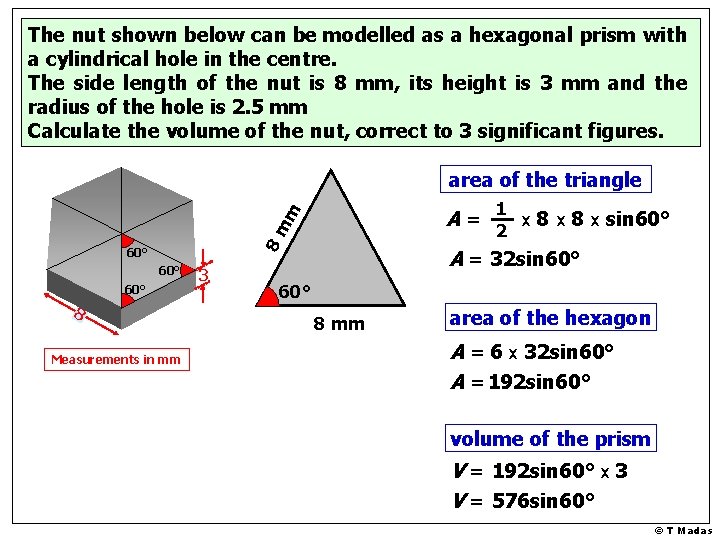
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. area of the triangle m A = 1 x 8 x sin 60° 8 m 2 60° 60° 8 Measurements in mm 3 A = 32 sin 60° 8 mm area of the hexagon A = 6 x 32 sin 60° A = 192 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas

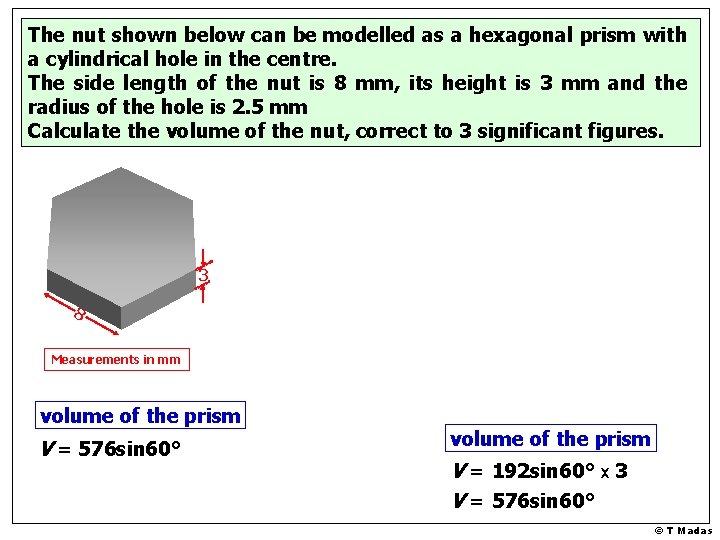
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. 3 8 Measurements in mm volume of the prism V = 576 sin 60° volume of the prism V = 192 sin 60° x 3 V = 576 sin 60° © T Madas

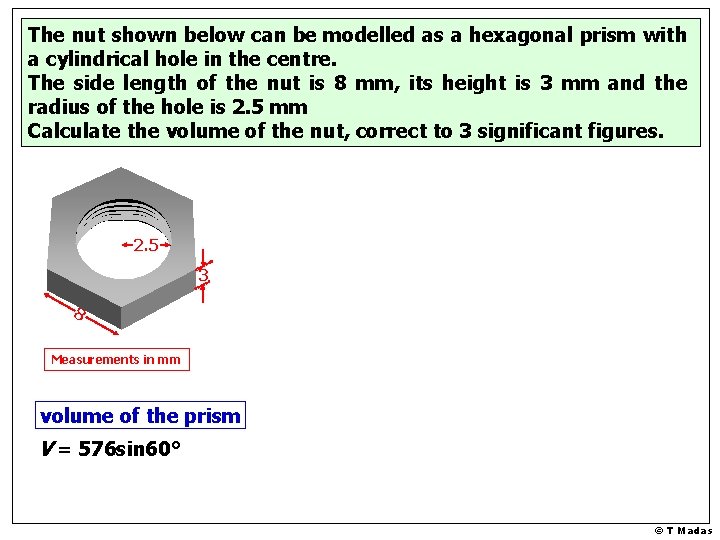
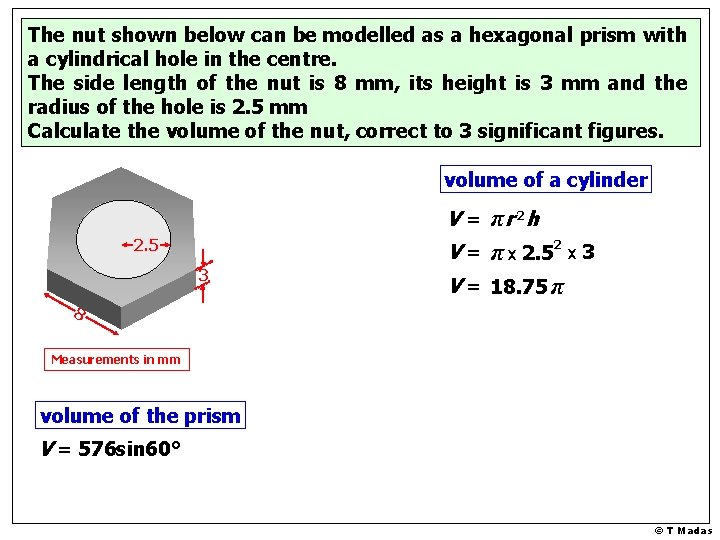
The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 3 2 V = π x 2. 5 x 3 V = 18. 75 π Measurements in mm volume of the prism V = 576 sin 60° © T Madas

The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the prism V = 576 sin 60° © T Madas

The nut shown below can be modelled as a hexagonal prism with a cylindrical hole in the centre. The side length of the nut is 8 mm, its height is 3 mm and the radius of the hole is 2. 5 mm Calculate the volume of the nut, correct to 3 significant figures. volume of a cylinder V = π r 2 h 2. 5 2 V = π x 2. 5 x 3 3 V = 18. 75 π 8 Measurements in mm volume of the nut volume of the prism 576 sin 60° – 18. 75 π V = 576 sin 60° 440 mm 3 [ 3 s. f. ] © T Madas

A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π x 4. 4 x 12 V ≈ 730 cm 3 If the measurements are to the nearest mm, then: 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 V = π r 2 h V = π x 4. 352 x 11. 95 c c 2 lower bound of the volume V ≈ 710 cm 3 upper bound of the volume V = π r 2 h V = π x 4. 452 x 12. 05 c c V = πr h 2 c c volume of the cylinder V ≈ 750 cm 3 © T Madas

A cylinder has a height of 12 cm and the radius of its base is 4. 4 cm. These measurements are correct to the nearest mm. Calculate: 1. the volume of the cone to the nearest cm 3. 2. the upper and lower bound for this volume to the nearest cm 3. 3. the percentage error if the actual volume is 715 cm 3 and we use the figure we found in part (1) instead. V = π r 2 h V = π x 4. 42 x 12 c c volume of the cylinder V ≈ 730 cm 3 If the measurements are to the nearest mm, then: If we use the figure of 730 cm 3 instead of 715 cm 3 … … we have an error of 15 cm 3 … … calculated over the actual volume of 715 cm 3 … 15 x 100 ≈ 2. 1% 715 4. 35 ≤ r < 4. 45 11. 95 ≤ h < 12. 05 © T Madas