VOLUME OF SOLIDS VOLUME OF SOLIDS DEFINITION is

VOLUME OF SOLIDS

VOLUME OF SOLIDS DEFINITION: -is the amount of space enclosed in a solid figure. The volume of a solid is the number of cubic units contained in the solid.

VOLUME OF SOLIDS In finding volume of solids, you have to consider the area of a base and height of the solid. If the base is triangular, you have to make use of the area of a triangle, if rectangular, make use of the area of a rectangle and so on.

CYLINDERS COMMON SOLIDS

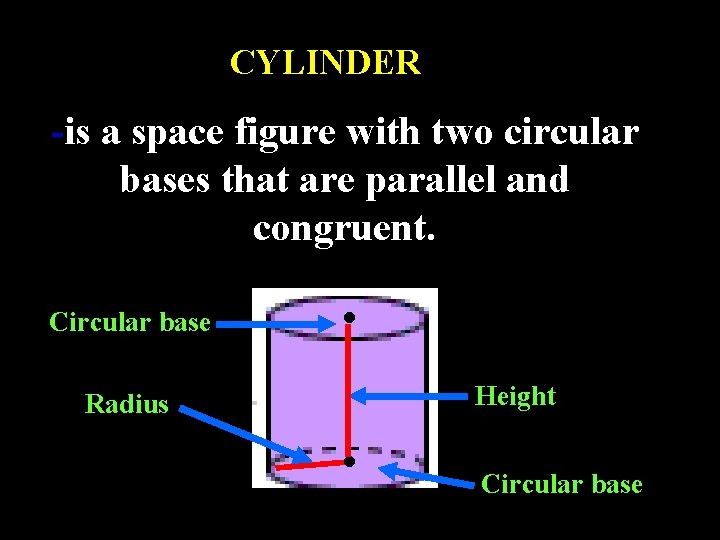
CYLINDER -is a space figure with two circular bases that are parallel and congruent. Circular base Radius . . Height Circular base

Volume of a cylinder n How can the volume of a cylinder be computed? n V = Bh, where B is the area of the base and h is the height of the cylinder. n by substitution, n V= πr²h

EXAMPLE 8: Find the volume of a cylinder. Use π = 3. 14 Solution: n. V = πr²h n =(3. 14)(5 cm)² 10 cm = 3. 14( 25 cm²) (10 cm) n = 3. 14( 250 cm³) n n. V = 785 cm³ 10 cm 5 cm

VOLUME OF A CONE REFLECTIVE TRAFFIC CONE

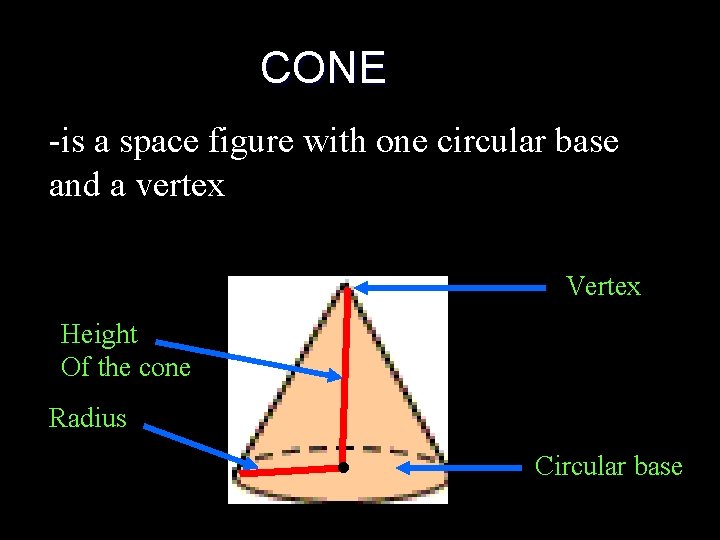
CONE -is a space figure with one circular base and a vertex Vertex Height Of the cone Radius . Circular base

VOLUME of a CONE • Consider a CONE and a CYLINDER having equal heights and bases with equal areas. • https: //www. youtube. com/watc h? v=0 ZACAU 4 SGy. M try using this link to watch a demonstration of a 3 cones filling up a cylinder. TURN YOUR VOLUME OFF!!! • If it doesn’t work, just skip this slide, it is just neat(: h r

Volume of a cone n How can the volume of a cone be computed? n V = ⅓Bh, where B is the area of the base and h is the height of the cone. n by substitution, n V= ⅓ πr²h

Find the volume of a cone. Use π = 3. 14 Solution: n. V n n n = ⅓ πr²h = ⅓(3. 14)(5 cm) ²(10 cm) = ⅓ (3. 14)(25 cm²) (10 cm) = ⅓ (785 cm³) n V= 261. 67 cm³ 10 cm 5 cm

VOLUME OF A SPHERE THE EARTH BALLS

SPHERE A sphere is a solid where every point is equally distant from its center. This distance is the length of the radius of a sphere. radius

VOLUME OF A SPHERE BALL The formula to find the VOLUMEof a sphere is V = πr³, where r is the length of its radius.

Archimedes of Syracuse (287 -212 BC) is regarded as the greatest of Greek mathematicians, and was also an inventor of many mechanical devices (including the screw, the pulley, and the lever). He perfected integration using Eudoxus' method of exhaustion, and found the areas and volumes of many objects.

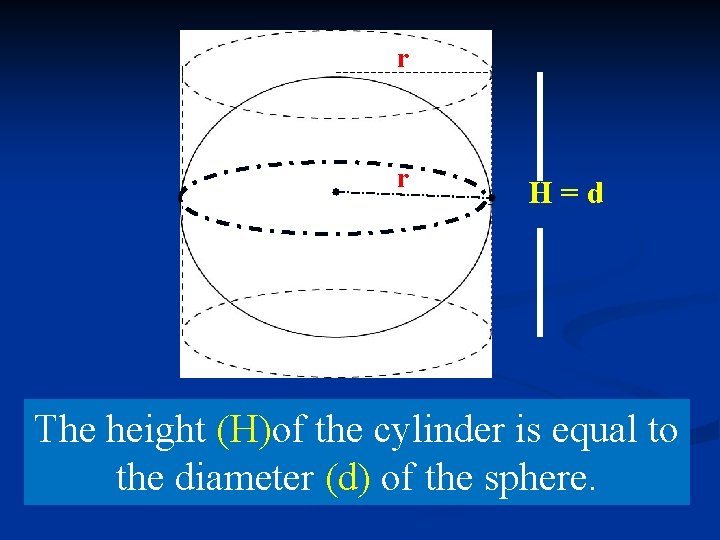
Archimedes of Syracuse (287 -212 BC) A famous result of his is that the volume of a sphere is two- thirds the volume of its circumscribed cylinder, a picture of which was inscribed on his tomb.

radius r r radius H=d The height (H)of the cylinder is equal to the diameter (d) of the sphere.

1. Find the volume of a sphere. Use π = 3. 14 Solution: n n V = 4/3 πr³ =4/3(3. 14)(10 cm)³ = 12. 56 (1000 cm³) 3 n = 12, 560 cm³) 3 n n V= 4, 186. 67 cm³ 10 cm

2. Find the volume of a sphere. Use π = 3. 14 Solution: n n V = 4/3 πr³ =4/3(3. 14)(7. 8 cm)³ = 12. 56 (474. 552 cm³) 3 n = 5960. 37312 cm³ 3 n n V= 1, 986. 79 cm³ 7. 8 cm