SVD Singular Value Decomposition Motivation Assume A full

SVD: Singular Value Decomposition

Motivation Assume A full rank Clearly the winner 2

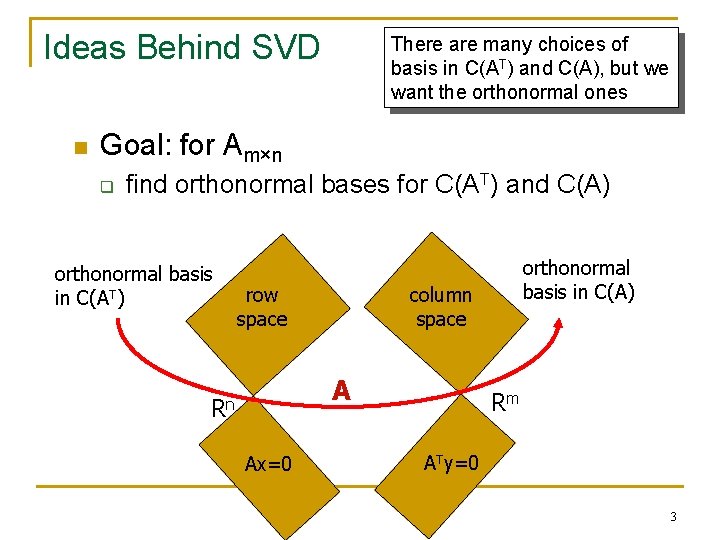
Ideas Behind SVD n There are many choices of basis in C(AT) and C(A), but we want the orthonormal ones Goal: for Am×n q find orthonormal bases for C(AT) and C(A) orthonormal basis in C(AT) row space column space A Rn Ax=0 orthonormal basis in C(A) Rm ATy=0 3

SVD (2 X 2) I haven’t told you how to find vi’s (p. 9) s: represent the length of images; hence nonnegative 4

SVD 2 x 2 (cont) Another diagonalization using 2 sets of orthogonal bases Compare When A has complete set of e-vectors, we have AS=SL , A=SLS-1 but S in general is not orthogonal When A is symmetric, we have A=QLQT 5

Why are orthonormal bases good? n n ( )-1=( )T Implication: q Matrix inversion q Ax=b 6

More on U and V V: eigenvectors of ATA U: eigenvectors of AAT [Find vi first, then use Avi to find ui This is the key to solve SVD 7

SVD: A=USVT n n n The singular values are the diagonal entries of the S matrix and are arranged in descending order The singular values are always real (nonnegative) numbers If A is real matrix, U and V are also real 8

Example (2 x 2, full rank) STEPS: 1. Find e-vectors of ATA; normalize the basis 2. Compute Avi, get si If si 0, get ui Else find ui from N(AT) 9

SVD Theory n If sj=0, Avj=0 vj is in N(A) q The corresponding uj in N(AT) n n Else, vj in C(AT) q n [UTA=SVT=0] The corresponding uj in C(A) #of nonzero sj = rank 10

Example (2 x 2, rank deficient) Can also be obtained from e -vectors of ATA 11

Example (cont) Bases of N(A) and N(AT) (u 2 and v 2 here) do not contribute the final result. The are computed to make U and V orthogonal. 12

Extend to Amxn Basis of N(A) Basis of N(AT) Dimension Check 13

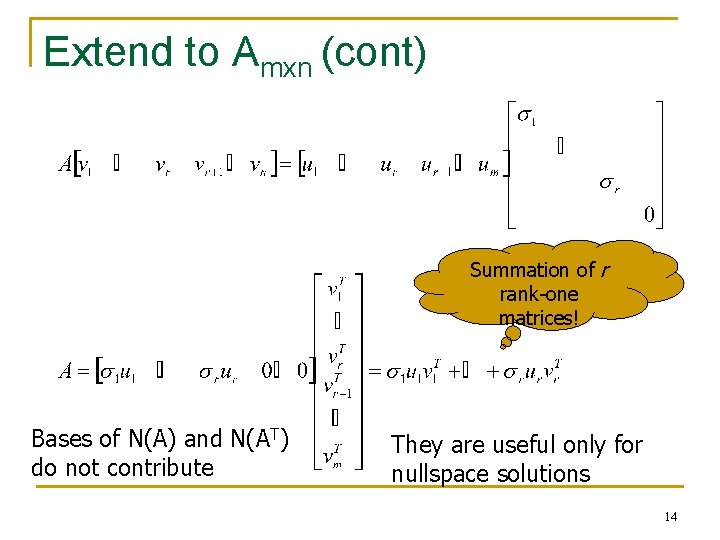
Extend to Amxn (cont) Summation of r rank-one matrices! Bases of N(A) and N(AT) do not contribute They are useful only for nullspace solutions 14

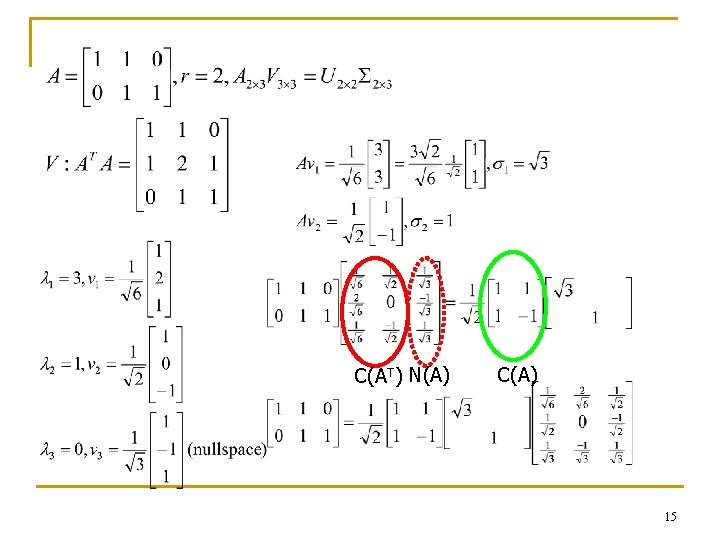
C(AT) N(A) C(A) 15

16

Summary n n SVD chooses the right basis for the 4 subspaces AV=US q q n n v 1…vr: orthonormal basis in Rn for C(AT) vr+1…vn: N(A) u 1…ur: in Rm C(A) ur+1…um: N(A T) These bases are not only , but also Avi=siui High points of Linear Algebra q Dimension, rank, orthogonality, basis, diagonalization, … 17

SVD Applications n n Using SVD in computation, rather than A, has the advantage of being more robust to numerical error Many applications: q q q n Inverse of matrix A Conditions of matrix Image compression Solve Ax=b for all cases (unique, many, no solutions; least square solutions) rank determination, matrix approximation, … SVD usually found by iterative methods (see Numerical Recipe, Chap. 2) 18

19

SVD and Ax=b (m n) n Check for existence of solution 20

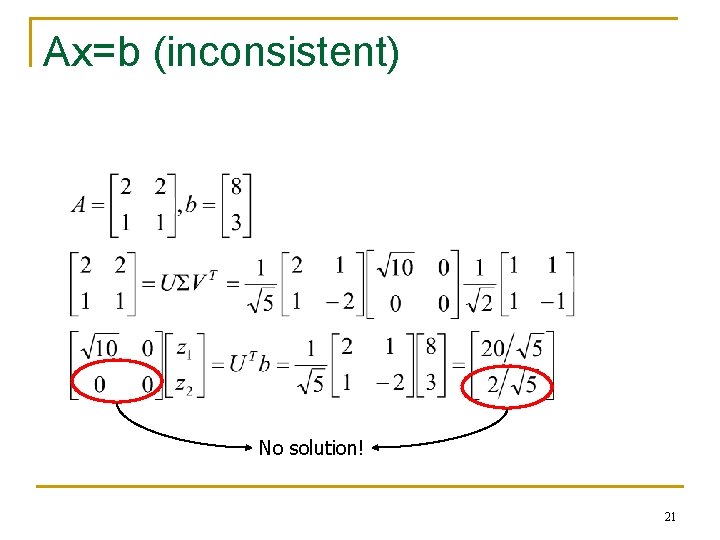
Ax=b (inconsistent) No solution! 21

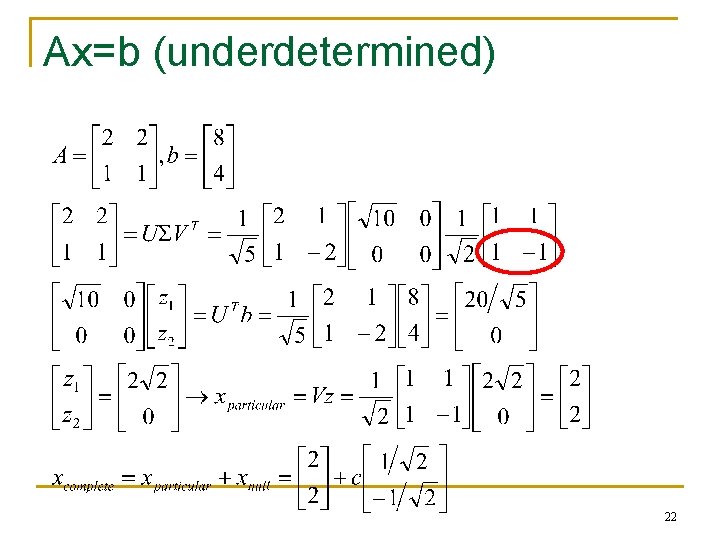
Ax=b (underdetermined) 22

Pseudo Inverse (Sec 7. 4, p. 395) n The role of A: q n Takes a vector vi from row space to siui in the column space The role of A-1 (if it exists): q Does the opposite: takes a vector ui from column space to row space vi 23

Pseudo Inverse (cont) n n While A-1 may not exist, a matrix that takes ui back to vi/si does exist. It is denoted as A+, the pseudo inverse A+: dimension n by m 24

Pseudo Inverse and Ax=b A panacea for Ax=b n Overdetermined case: find the solution that minimize the error r=|Ax–b|, the least square solution 25

Ex: full rank 26

Ex: over-determined Will show this need not be computed… 27

Over-determined (cont) Same result!! 28

Ex: general case, no solution 29

Matrix Approximation making small s’s to zero and back substitute (see next page for application in image compression) 30

Image Compression n As described in text p. 352 For grey scale images: m n bytes n Only need to store r (m+n+1) n Original 64 64 r = 1, 3, 5, 10, 16 (no perceivable difference afterwards) 31

32

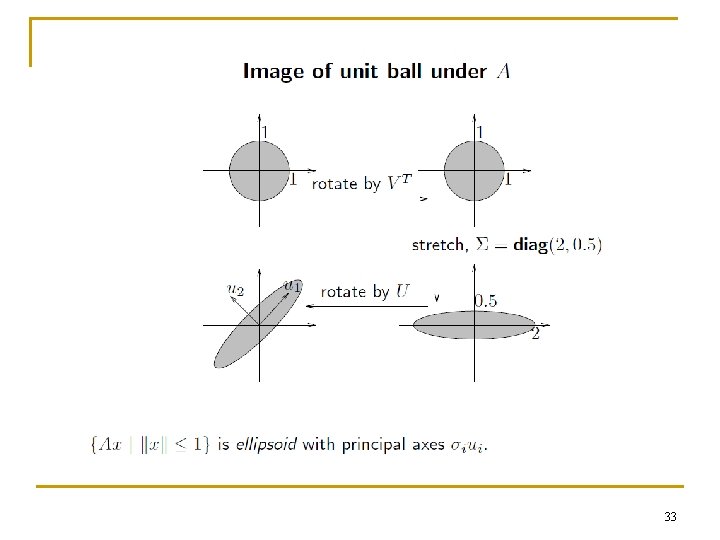
33