Functional Integration Dynamic Causal Modelling DCM Klaas Enno



























- Slides: 62

Functional Integration & Dynamic Causal Modelling (DCM) Klaas Enno Stephan & Lee Harrison Functional Imaging Lab Wellcome Dept. of Imaging Neuroscience University College London ICN SPM Course May 6 th, 2005

Overview • Classical approaches to functional & effective connectivity • Generic concepts of system analysis • DCM for f. MRI: – Neural dynamics and hemodynamics – Bayesian parameter estimation – – Interpretation of parameters Statistical inference Bayesian model selection Practical issues and a simple example • DCM for ERPs

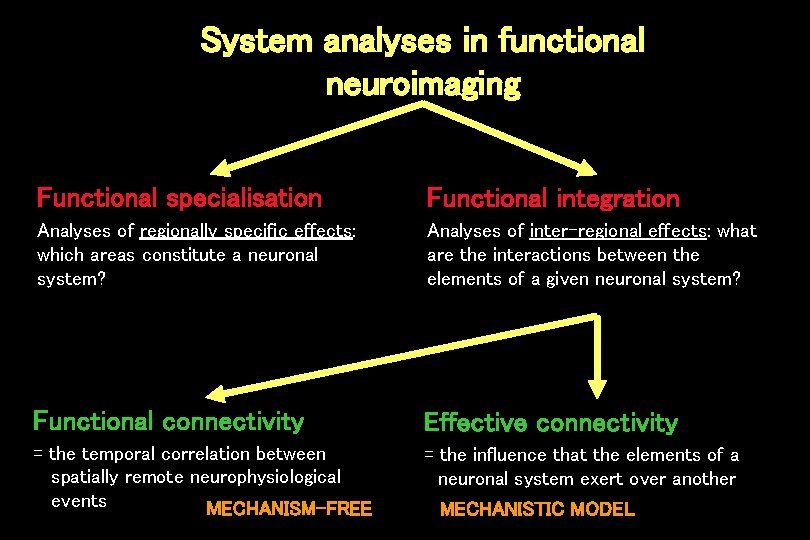
System analyses in functional neuroimaging Functional specialisation Functional integration Analyses of regionally specific effects: which areas constitute a neuronal system? Analyses of inter-regional effects: what are the interactions between the elements of a given neuronal system? Functional connectivity Effective connectivity = the temporal correlation between spatially remote neurophysiological events MECHANISM-FREE = the influence that the elements of a neuronal system exert over another MECHANISTIC MODEL

Functional connectivity: methods • Seed-voxel correlation analyses • Eigenimage analysis – Principal Components Analysis (PCA) – Singular Value Decomposition (SVD) – Partial Least Squares (PLS) • Independent Component Analysis (ICA)

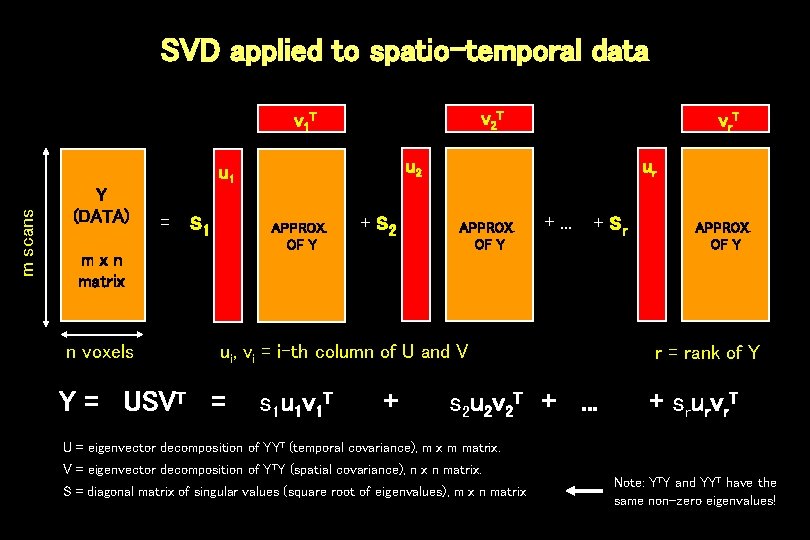
Eigen-decomposition: some general maths Definition of eigenvector e and eigenvalue : Ae = e e e Geometric meaning: Eigenvectors are only scaled by Y; their direction is unchanged principal axes of the matrix operation PCA: Y* = EY Re-expresses Y in terms of a new orthonormal basis E, the eigenvectors of the covariance matrix YYT. The new axes account for extreme and orthogonal components of the covariance structure. SVD: Y = USVT A general method for eigen-decomposition of matrices. If dealing with spatio-temporal data, SVD re-expresses Y in terms of the eigenvectors of the spatial and temporal covariance matrices.

SVD applied to spatio-temporal data v 2 T v 1 T u 2 m scans u 1 Y (DATA) = s 1 APPROX. OF Y mxn matrix n voxels v r. T + s 2 ur APPROX. OF Y +. . . + ui, vi = i-th column of U and V Y = USVT = s 1 u 1 v 1 T + s 2 u 2 v 2 T +. . . sr APPROX. OF Y r = rank of Y + srurvr. T U = eigenvector decomposition of YYT (temporal covariance), m x m matrix. V = eigenvector decomposition of YTY (spatial covariance), n x n matrix. S = diagonal matrix of singular values (square root of eigenvalues), m x n matrix Note: YTY and YYT have the same non-zero eigenvalues!

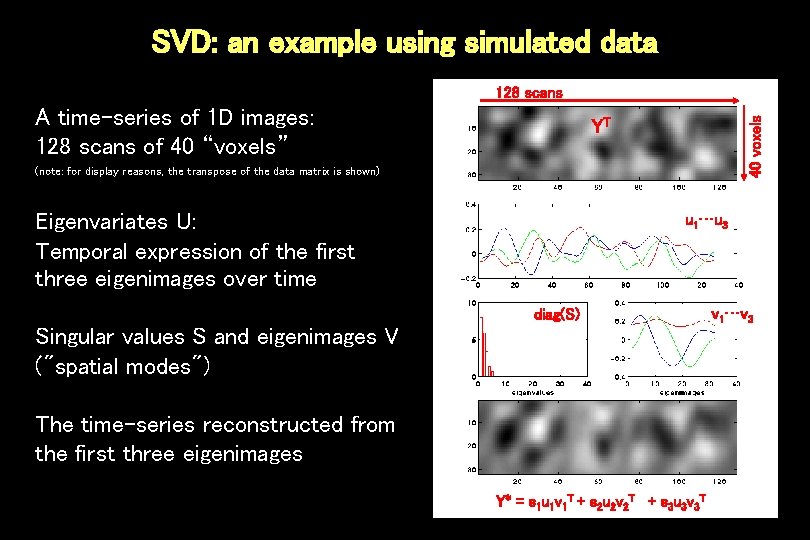
SVD: an example using simulated data A time-series of 1 D images: 128 scans of 40 “voxels” 40 voxels 128 scans YT (note: for display reasons, the transpose of the data matrix is shown) Eigenvariates U: Temporal expression of the first three eigenimages over time u 1…u 3 diag(S) Singular values S and eigenimages V ("spatial modes") The time-series reconstructed from the first three eigenimages Y* = s 1 u 1 v 1 T + s 2 u 2 v 2 T + s 3 u 3 v 3 T v 1…v 3

Pros & Cons of functional connectivity • Pros: – useful when we have no model of what caused the data (e. g. sleep, hallucinatons, etc. ) • Cons: – no mechanistic insight into the neural system of interest – inappropriate for situations where we have a priori knowledge and experimental control about the system of interest models of effective connectivity necessary

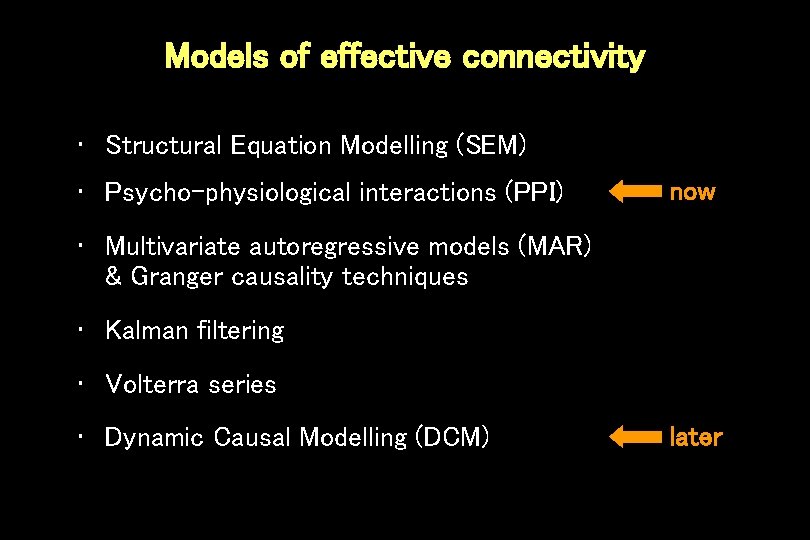
Models of effective connectivity • Structural Equation Modelling (SEM) • Psycho-physiological interactions (PPI) now • Multivariate autoregressive models (MAR) & Granger causality techniques • Kalman filtering • Volterra series • Dynamic Causal Modelling (DCM) later

Psycho-physiological interaction (PPI) Task factor GLM of a 2 x 2 factorial design: interaction We can replace one main effect in the GLM by the time series of an area that shows this main effect. E. g. let's replace the main effect of stimulus type by the time series of V 1: Stim 1 main effect of stim. type Task B TA/S 1 TB/S 1 Stim 2 main effect of task Stimulus factor Task A TA/S 2 TB/S 2 main effect of task V 1 time series main effect of stim. type psychophysiological interaction

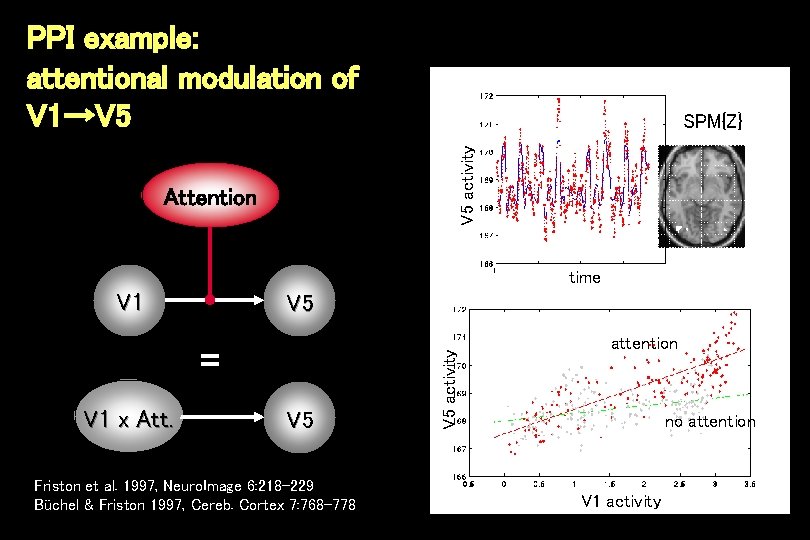
PPI example: attentional modulation of V 1→V 5 activity SPM{Z} Attention time V 1 = V 1 x Att. V 5 Friston et al. 1997, Neuro. Image 6: 218 -229 Büchel & Friston 1997, Cereb. Cortex 7: 768 -778 V 5 activity V 5 attention no attention V 1 activity

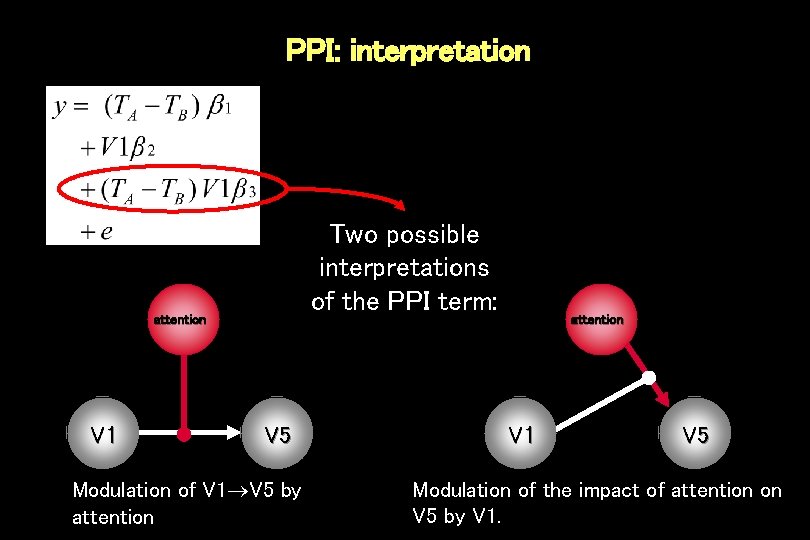
PPI: interpretation Two possible interpretations of the PPI term: attention V 1 V 5 Modulation of V 1 V 5 by attention V 1 V 5 Modulation of the impact of attention on V 5 by V 1.

Pros & Cons of PPIs • Pros: – given a single source region, we can test for its context-dependent connectivity across the entire brain • Cons: – very simplistic model: only allows to model contributions from a single area – ignores time-series properties of data – not easily used with event-related data – operates at the level of BOLD time series limited causal interpretability in neural terms, more powerful models needed DCM!

Overview • Classical approaches to functional & effective connectivity • Generic concepts of system analysis • DCM for f. MRI: – Neural dynamics and hemodynamics – Bayesian parameter estimation – – Interpretation of parameters Statistical inference Bayesian model selection Practical issues and a simple example • DCM for ERPs

Models of effective connectivity = system models. But what precisely is a system? • System = set of elements which interact in a spatially and temporally specific fashion. • System dynamics = change of state vector in time overall system state represented by state variables • Causal effects in the system: – interactions between elements – external inputs u • System parameters : specify the nature of the interactions • general state equation for nonautonomous systems change of state vector in time

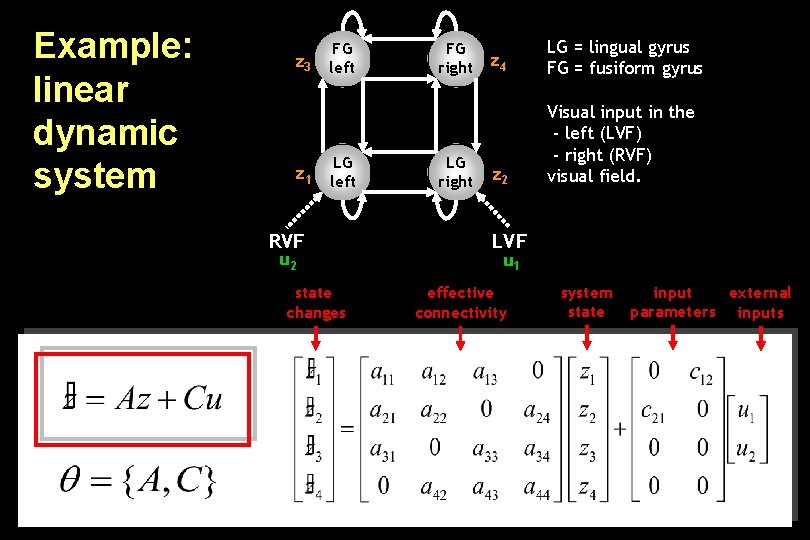
Example: linear dynamic system FG z 3 left z 1 LG left RVF u 2 state changes FG right LG right z 4 LG = lingual gyrus FG = fusiform gyrus z 2 Visual input in the - left (LVF) - right (RVF) visual field. LVF u 1 effective connectivity system state input external parameters inputs

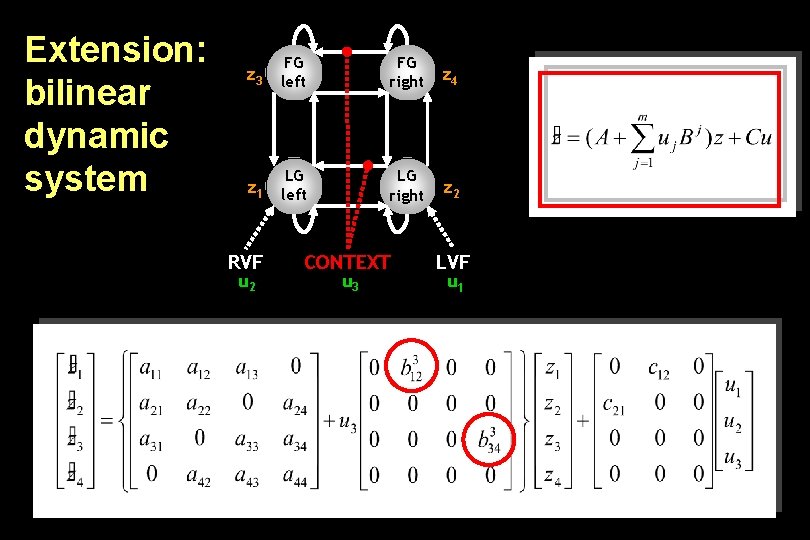
Extension: bilinear dynamic system z 3 FG left FG right z 4 z 1 LG left LG right z 2 RVF u 2 CONTEXT u 3 LVF u 1

Bilinear state equation in DCM state changes intrinsic connectivity modulation of system connectivity state direct inputs m external inputs

DCM for f. MRI: the basic idea • Using a bilinear state equation, a cognitive system is modelled at its underlying neuronal level (which is not directly accessible for f. MRI). • The modelled neuronal dynamics (z) is transformed into area-specific BOLD signals (y) by a hemodynamic forward model (λ). The aim of DCM is to estimate parameters at the neuronal level such that the modelled BOLD signals are maximally similar to the experimentally measured BOLD signals. z λ y

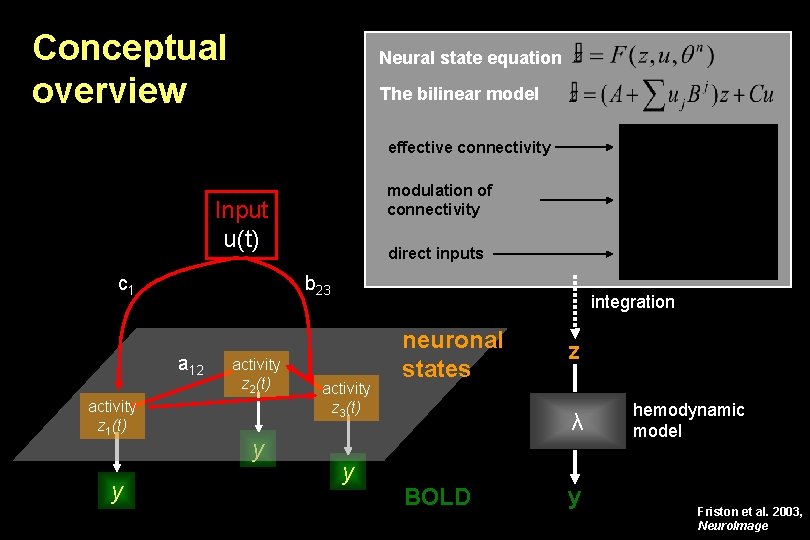
Conceptual overview Neural state equation The bilinear model effective connectivity modulation of connectivity Input u(t) c 1 b 23 a 12 activity z 1(t) y direct inputs activity z 2(t) y integration activity z 3(t) y neuronal states z λ BOLD y hemodynamic model Friston et al. 2003, Neuro. Image

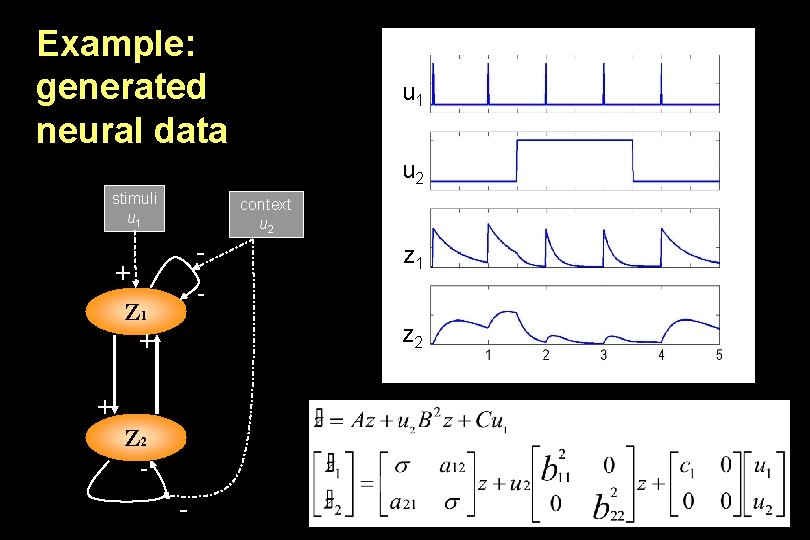
Example: generated neural data stimuli u 1 u 1 u 2 context u 2 - + - Z 1 + u 2 Z 1 z Z 2 1 z 2 + Z 2 -

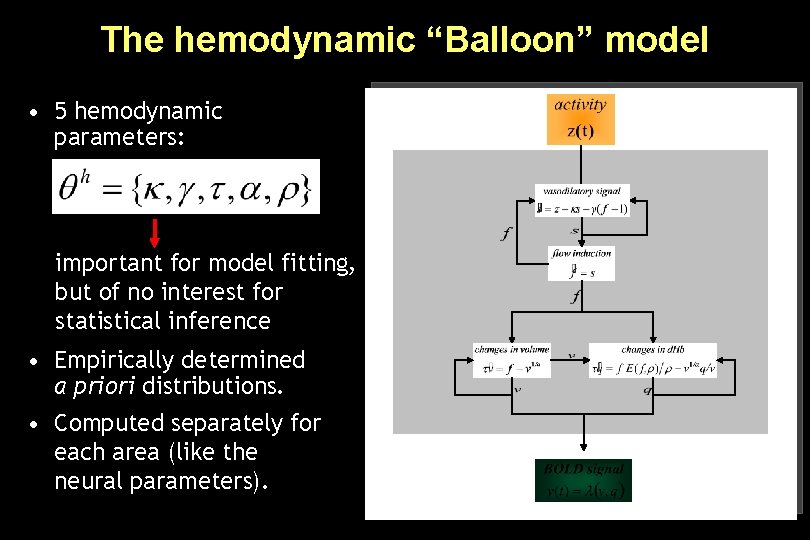
The hemodynamic “Balloon” model • 5 hemodynamic parameters: important for model fitting, but of no interest for statistical inference • Empirically determined a priori distributions. • Computed separately for each area (like the neural parameters).

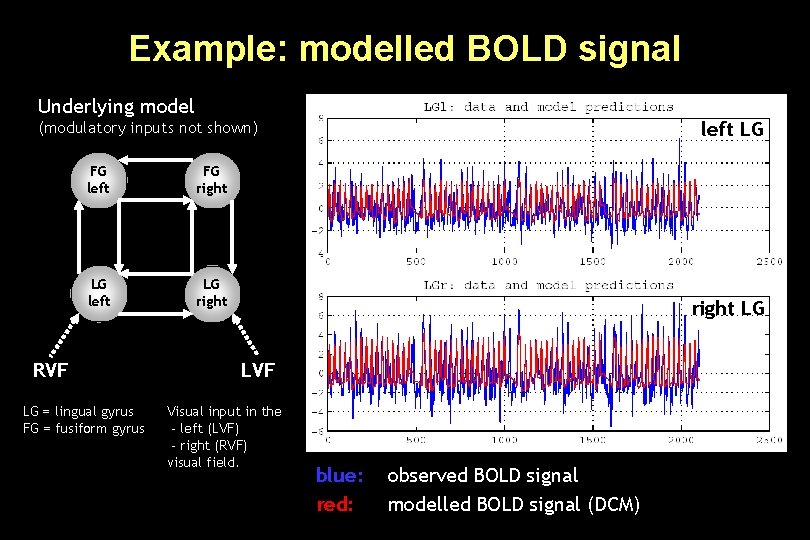
Example: modelled BOLD signal Underlying model left LG (modulatory inputs not shown) FG left FG right LG left LG right RVF LG = lingual gyrus FG = fusiform gyrus right LG LVF Visual input in the - left (LVF) - right (RVF) visual field. blue: red: observed BOLD signal modelled BOLD signal (DCM)

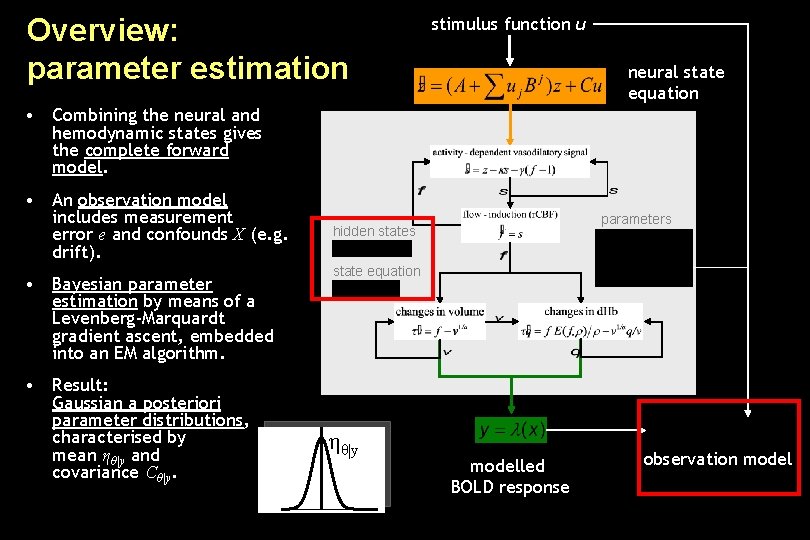
Overview: parameter estimation stimulus function u neural state equation • Combining the neural and hemodynamic states gives the complete forward model. • An observation model includes measurement error e and confounds X (e. g. drift). • Bayesian parameter estimation by means of a Levenberg-Marquardt gradient ascent, embedded into an EM algorithm. • Result: Gaussian a posteriori parameter distributions, characterised by mean ηθ|y and covariance Cθ|y. parameters hidden states state equation ηθ|y modelled BOLD response observation model

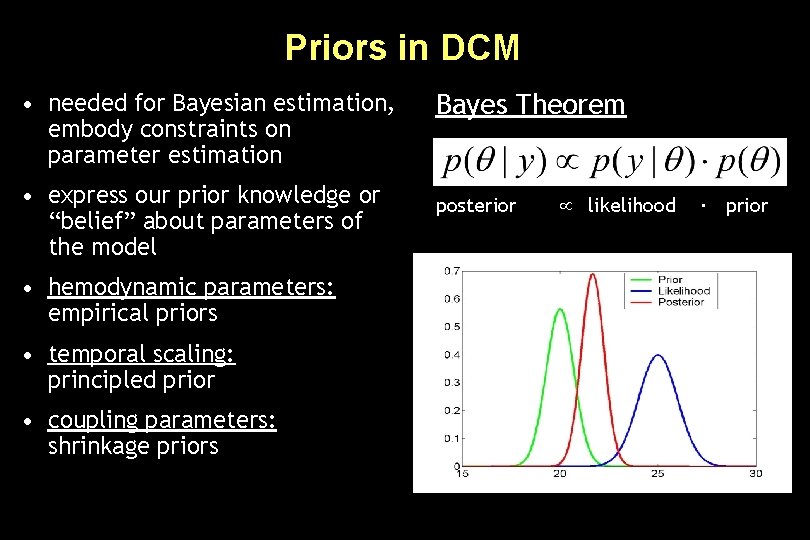
Priors in DCM • needed for Bayesian estimation, embody constraints on parameter estimation • express our prior knowledge or “belief” about parameters of the model • hemodynamic parameters: empirical priors • temporal scaling: principled prior • coupling parameters: shrinkage priors Bayes Theorem posterior likelihood ∙ prior

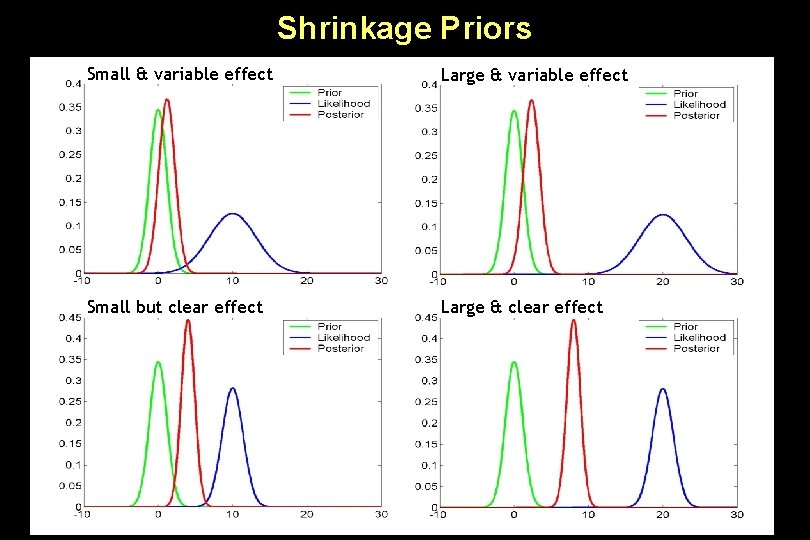
Priors in DCM • system stability: in the absence of input, the neuronal states must return to a stable mode → constraints on prior variance of intrinsic connections (A) → probability <0. 001 of obtaining a non-negative Lyapunov exponent (largest real eigenvalue of the intrinsic coupling matrix) • shrinkage priors for coupling parameters (η=0) → conservative estimates! • self-inhibition: ensured by priors on the decay rate constant σ (ησ=1, Cσ=0. 105) → these allow for neural transients with a half life in the range of 300 ms to 2 seconds NB: a single rate constant for all regions! • Identical temporal scaling in all areas by factorising A and B with σ: all connection strengths are relative to the self-connections.

Shrinkage Priors Small & variable effect Large & variable effect Small but clear effect Large & clear effect

Parameter estimation in DCM • Combining the neural and hemodynamic states gives the complete forward model: • Bayesian parameter estimation under Gaussian assumptions by means of EM and gradient ascent. • Result: Gaussian a posteriori parameter distributions, characterised by mean ηθ|y and covariance Cθ|y. • The observation model includes measurement error and confounds X (e. g. drift): ηθ|y

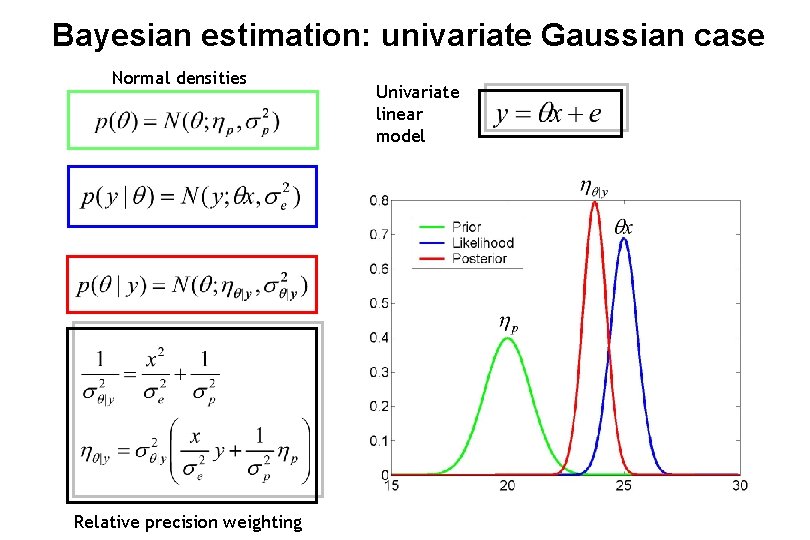
Bayesian estimation: univariate Gaussian case Normal densities Relative precision weighting Univariate linear model

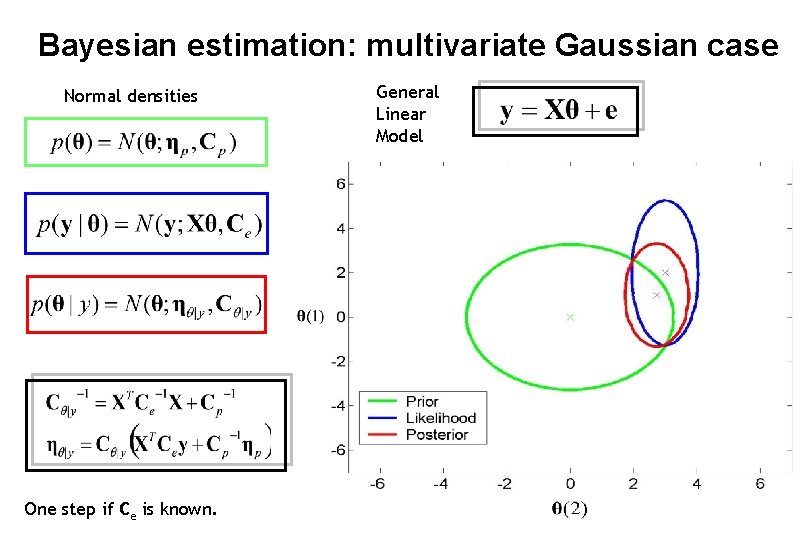
Bayesian estimation: multivariate Gaussian case Normal densities One step if Ce is known. General Linear Model

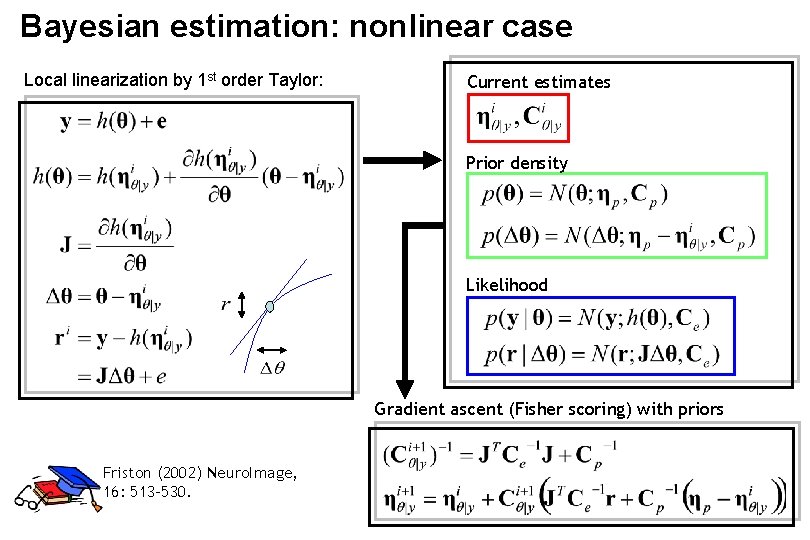
Bayesian estimation: nonlinear case Local linearization by 1 st order Taylor: Current estimates Prior density Likelihood Gradient ascent (Fisher scoring) with priors Friston (2002) Neuro. Image, 16: 513 -530.

EM and gradient ascent • Bayesian parameter estimation by means of expectation maximisation (EM) – E-step: gradient ascent (Fisher scoring & Levenberg-Marquardt regularisation) on the log posterior to compute • (i) the conditional mean ηθ|y (= expansion point of gradient ascent), • (ii) the conditional covariance Cθ|y – M-step: Re. ML estimates of hyperparameters i for error covariance components Qi: • Note: Gaussian assumptions about the posterior (Laplace approximation)

E-step: Fisher scoring Generally, Fisher scoring is identical to the Gauss-Newton algorithm (except that the expectation of the Hessian is taken): For DCM, the Fisher scoring scheme can be derived by taking partial derivatives of the log posterior wrt. to the parameters: This results in equations equivalent to those derived for posterior mode estimation in non-linear cases, using local linearisation (see previous slides) :

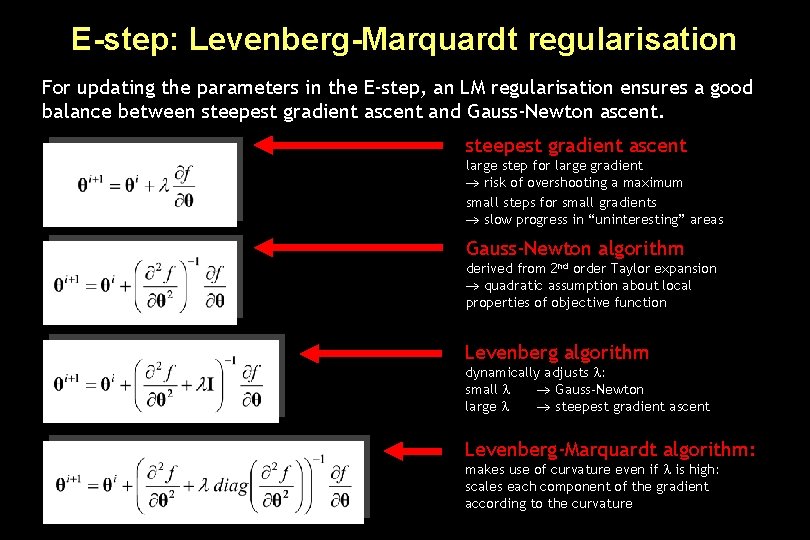
E-step: Levenberg-Marquardt regularisation For updating the parameters in the E-step, an LM regularisation ensures a good balance between steepest gradient ascent and Gauss-Newton ascent. steepest gradient ascent large step for large gradient risk of overshooting a maximum small steps for small gradients slow progress in “uninteresting” areas Gauss-Newton algorithm derived from 2 nd order Taylor expansion quadratic assumption about local properties of objective function Levenberg algorithm dynamically adjusts : small Gauss-Newton large steepest gradient ascent Levenberg-Marquardt algorithm: makes use of curvature even if is high: scales each component of the gradient according to the curvature

Parameter estimation (new): output in command window E-Step: 1 F: -1. 514001 e+003 dp: 8. 299907 e-002 E-Step: 2 F: -1. 200724 e+003 dp: 9. 638851 e-001 E-Step: 3 F: -1. 115951 e+003 dp: 2. 703493 e-001 E-Step: 4 F: -1. 077757 e+003 dp: 2. 002973 e-002 E-Step: 5 F: -1. 075699 e+003 dp: 4. 219233 e-003 E-Step: 6 F: -1. 075663 e+003 dp: 1. 030322 e-003 E-Step: 7 F: -1. 075661 e+003 dp: 3. 595806 e-004 E-Step: 8 F: -1. 075661 e+003 dp: 2. 273264 e-006 Change of the norm of the parameter vector (= magnitude of update) objective function

Overview • Classical approaches to functional & effective connectivity • Generic concepts of system analysis • DCM for f. MRI: – Neural dynamics and hemodynamics – Bayesian parameter estimation – – Interpretation of parameters Statistical inference Bayesian model selection Practical issues and a simple example • DCM for ERPs

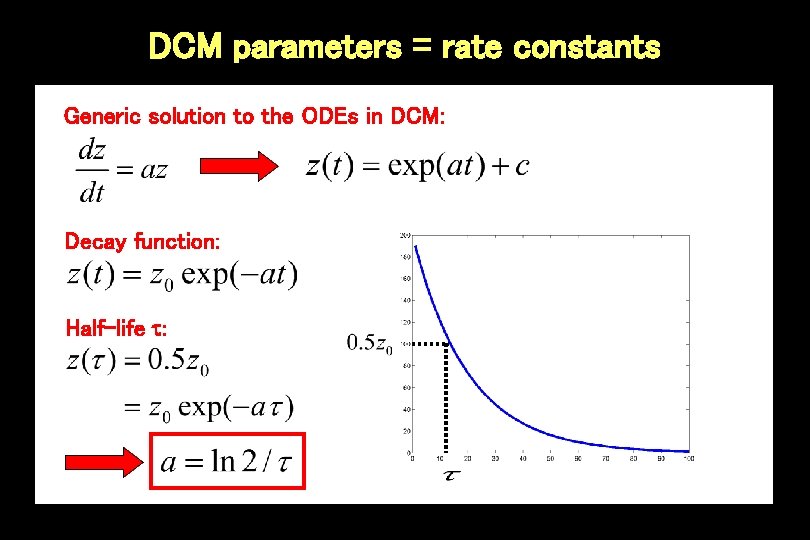
DCM parameters = rate constants Generic solution to the ODEs in DCM: Decay function: Half-life :

Inference about DCM parameters: Bayesian single-subject analysis • Bayesian parameter estimation in DCM: Gaussian assumptions about the posterior distributions of the parameters • Use of the cumulative normal distribution to test the probability by which a certain parameter (or contrast of parameters c. T ηθ|y) is above a chosen threshold γ: ηθ |y • γ can be chosen as zero ("does the effect exist? ") or as a function of the expected half life τ of the neural process: γ = ln 2 / τ

Inference about DCM parameters: Bayesian fixed-effects group analysis Because the likelihood distributions from different subjects are independent, one can combine their posterior densities by using the posterior of one subject as the prior for the next: See: spm_dcm_average. m Neumann & Lohmann, Neuro. Image 2003 Under Gaussian assumptions this is easy to compute: group posterior covariance group posterior mean individual posterior covariances and means

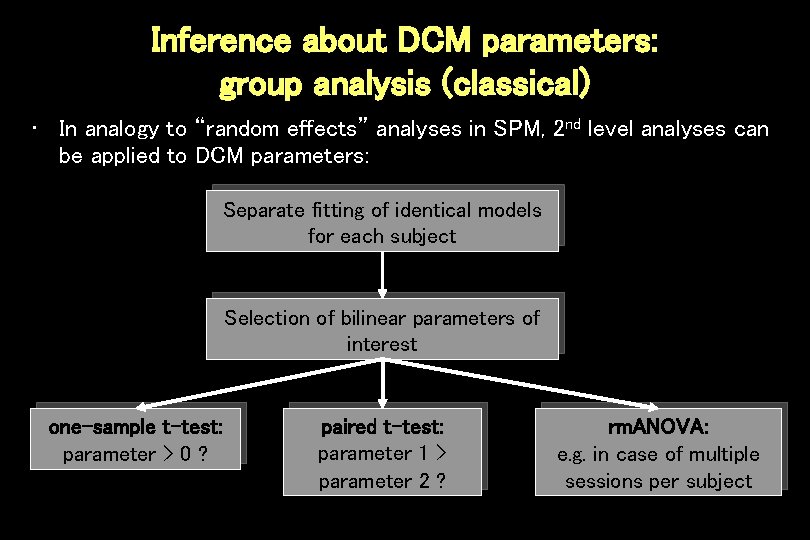
Inference about DCM parameters: group analysis (classical) • In analogy to “random effects” analyses in SPM, 2 nd level analyses can be applied to DCM parameters: Separate fitting of identical models for each subject Selection of bilinear parameters of interest one-sample t-test: parameter > 0 ? paired t-test: parameter 1 > parameter 2 ? rm. ANOVA: e. g. in case of multiple sessions per subject

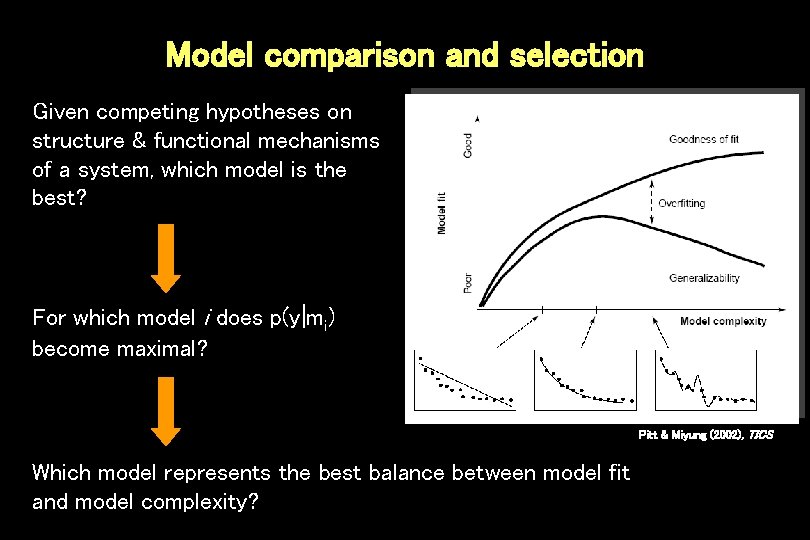
Model comparison and selection Given competing hypotheses on structure & functional mechanisms of a system, which model is the best? For which model i does p(y|mi) become maximal? Pitt & Miyung (2002), TICS Which model represents the best balance between model fit and model complexity?

Bayesian Model Selection Bayes theorem: Model evidence: The log model evidence can be represented as: Bayes factor: Penny et al. 2004, Neuro. Image

Approximations to model evidence Laplace approximation: Unfortunately, the complexity term depends on the prior density, which is determined individually for each model to ensure stability. Therefore, we need other approximations to the model evidence. Akaike information criterion (AIC): Bayesian information criterion (BIC): Penny et al. 2004, Neuro. Image

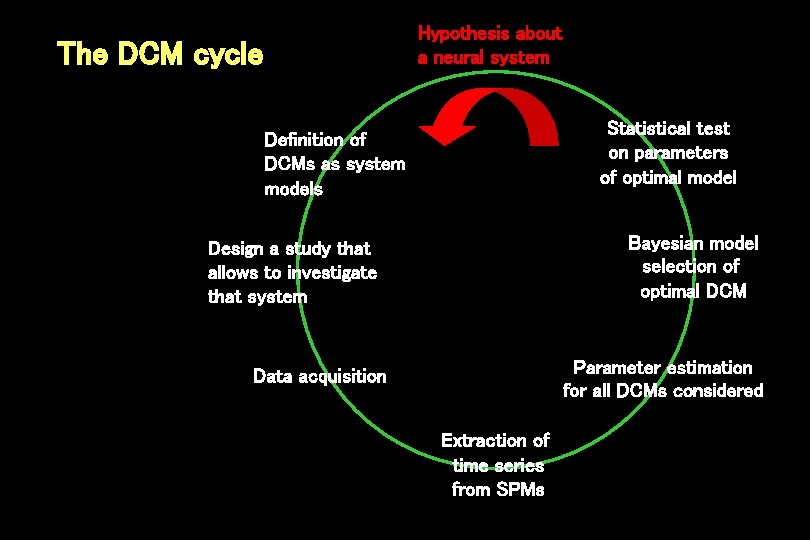
Hypothesis about a neural system The DCM cycle Statistical test on parameters of optimal model Definition of DCMs as system models Bayesian model selection of optimal DCM Design a study that allows to investigate that system Parameter estimation for all DCMs considered Data acquisition Extraction of time series from SPMs

Planning a DCM-compatible study • Suitable experimental design: – preferably multi-factorial (e. g. 2 x 2) – e. g. one factor that varies the driving (sensory) input – and one factor that varies the contextual input • TR: – as short as possible (optimal: < 2 s) • Hypothesis and model: – define specific a priori hypothesis – which parameters are relevant to test this hypothesis? – ensure that intended model is suitable to test this hypothesis → simulations before experiment – define criteria for inference

• • • Two potential timing problems in DCM: 1. wrong timing of inputs 2. temporal shift between regional time series because of multi-slice acquisition Timing problems at long TRs DCM is robust against timing errors up to approx. ± 1 s – compensatory changes of σ and θh Possible corrections: – slice-timing (not for long TRs) – restriction of the model to neighbouring regions – in both cases: adjust temporal reference bin in SPM defaults (defaults. stats. fmri. t 0) 2 1 visual input

Practical steps of a DCM study - I 1. Conventional SPM analysis (subject-specific) • DCMs are fitted separately for each session → consider concatenation of sessions or adequate 2 nd level analysis 2. Definition of the model (on paper!) • • Structure: which areas, connections and inputs? Which parameters represent my hypothesis? How can I demonstrate the specificity of my results? What are the alternative models to test? 3. Defining criteria for inference: • • single-subject analysis: group analysis: stat. threshold? contrast? which 2 nd-level model?

Practical steps of a DCM study - II 4. Extraction of time series, e. g. via VOI tool in SPM • cave: anatomical & functional standardisation important for group analyses! 5. Possibly definition of a new design matrix, if the “normal” design matrix does not represent the inputs appropriately. • NB: DCM only reads timing information of each input from the design matrix, no parameter estimation necessary. 6. Definition of model • via DCM-GUI or directly in MATLAB

Practical steps of a DCM study - III 7. DCM parameter estimation • cave: models with many regions & scans can crash MATLAB! 8. Model comparison and selection: • Which of all models considered is the optimal one? Bayesian model selection tool 9. Testing the hypothesis Statistical test on the relevant parameters of the optimal model

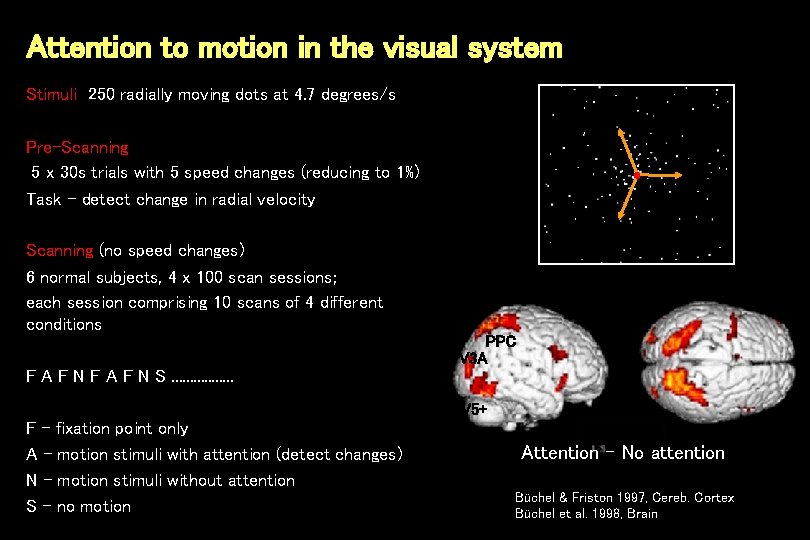
Attention to motion in the visual system Stimuli 250 radially moving dots at 4. 7 degrees/s Pre-Scanning 5 x 30 s trials with 5 speed changes (reducing to 1%) Task - detect change in radial velocity Scanning (no speed changes) 6 normal subjects, 4 x 100 scan sessions; each session comprising 10 scans of 4 different conditions PPC V 3 A F N F A F N S. . . . V 5+ F - fixation point only A - motion stimuli with attention (detect changes) N - motion stimuli without attention S - no motion Attention – No attention Büchel & Friston 1997, Cereb. Cortex Büchel et al. 1998, Brain

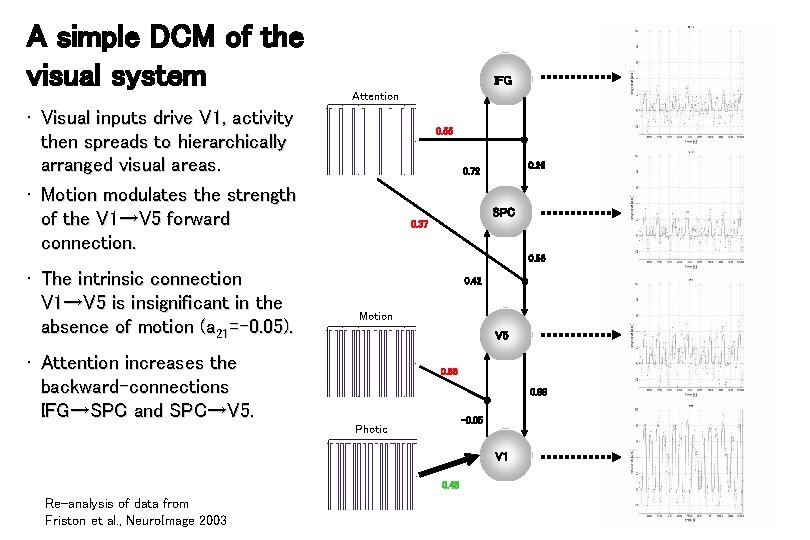
A simple DCM of the visual system IFG Attention • Visual inputs drive V 1, activity then spreads to hierarchically arranged visual areas. • Motion modulates the strength of the V 1→V 5 forward connection. 0. 55 0. 26 0. 72 SPC 0. 37 0. 56 • The intrinsic connection V 1→V 5 is insignificant in the absence of motion (a 21=-0. 05). 0. 42 Motion V 5 • Attention increases the backward-connections IFG→SPC and SPC→V 5. 0. 66 0. 88 -0. 05 Photic V 1 0. 48 Re-analysis of data from Friston et al. , Neuro. Image 2003

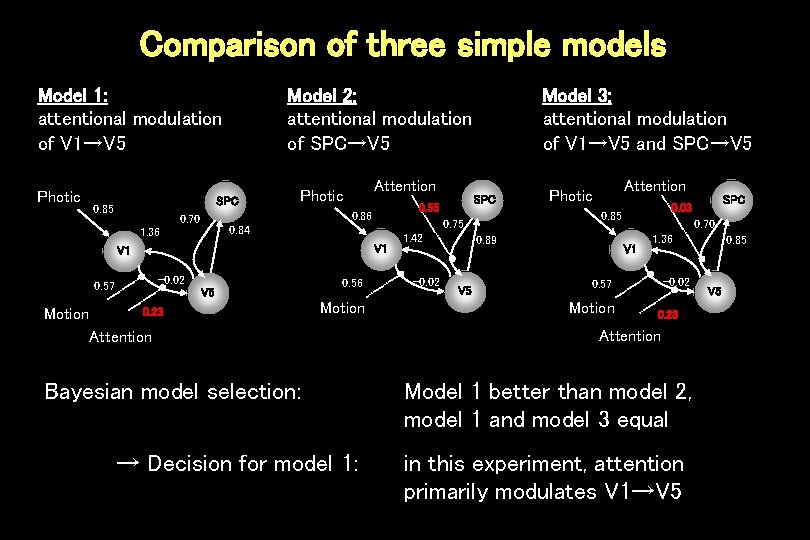
Comparison of three simple models Model 1: attentional modulation of V 1→V 5 Photic Model 2: attentional modulation of SPC→V 5 SPC 0. 85 Attention Photic V 1 -0. 02 0. 57 Motion V 5 0. 23 0. 56 Motion Attention Bayesian model selection: → Decision for model 1: 1. 42 -0. 02 Attention Photic 0. 89 V 5 0. 70 V 1 1. 36 -0. 02 0. 57 Motion SPC 0. 03 0. 85 0. 75 0. 84 1. 36 SPC 0. 55 0. 86 0. 70 Model 3: attentional modulation of V 1→V 5 and SPC→V 5 0. 23 Attention Model 1 better than model 2, model 1 and model 3 equal in this experiment, attention primarily modulates V 1→V 5 0. 85 V 5

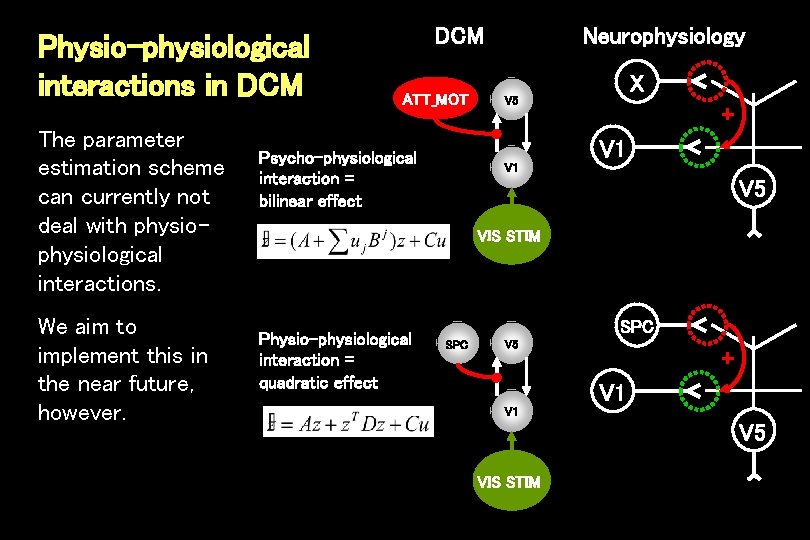
Physio-physiological interactions in DCM The parameter estimation scheme can currently not deal with physiological interactions. We aim to implement this in the near future, however. DCM ATT_MOT Neurophysiology X V 5 + V 1 Psycho-physiological interaction = bilinear effect V 1 V 5 VIS STIM Physio-physiological interaction = quadratic effect SPC V 5 + V 1 V 5 VIS STIM

Overview • Classical approaches to functional & effective connectivity • Generic concepts of system analysis • DCM for f. MRI: – Neural dynamics and hemodynamics – Bayesian parameter estimation – – Interpretation of parameters Statistical inference Bayesian model selection Practical issues and a simple example • DCM for ERPs (slides provided by Stefan Kiebel)

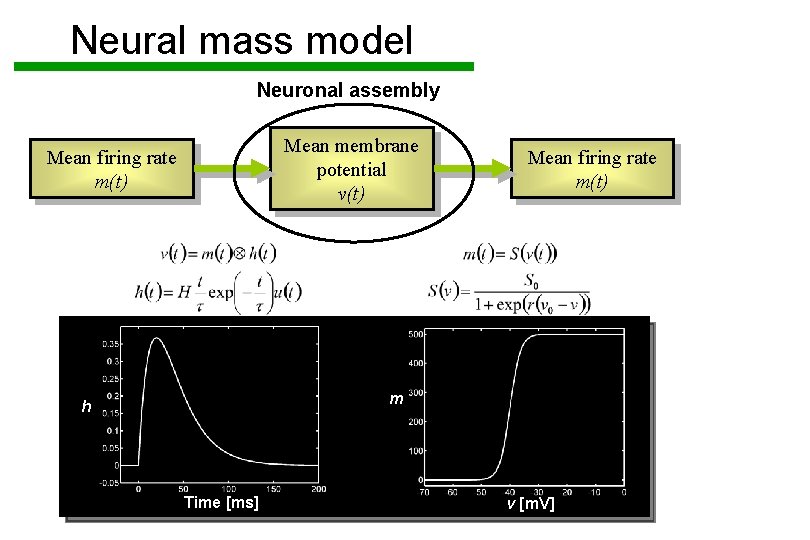
Neural mass model Neuronal assembly Mean membrane potential v(t) Mean firing rate m(t) m h Time [ms] v [m. V]

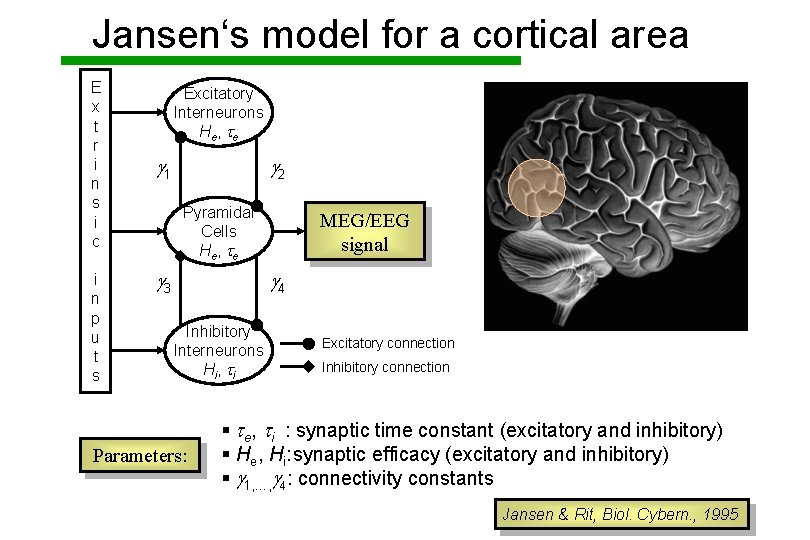
Jansen‘s model for a cortical area E x t r i n s i c i n p u t s Excitatory Interneurons He , t e g 1 g 2 Pyramidal Cells He , t e g 3 MEG/EEG signal g 4 Inhibitory Interneurons Hi , t i Parameters: Excitatory connection Inhibitory connection § te, ti : synaptic time constant (excitatory and inhibitory) § He, Hi: synaptic efficacy (excitatory and inhibitory) § g 1, …, g 4: connectivity constants Jansen & Rit, Biol. Cybern. , 1995

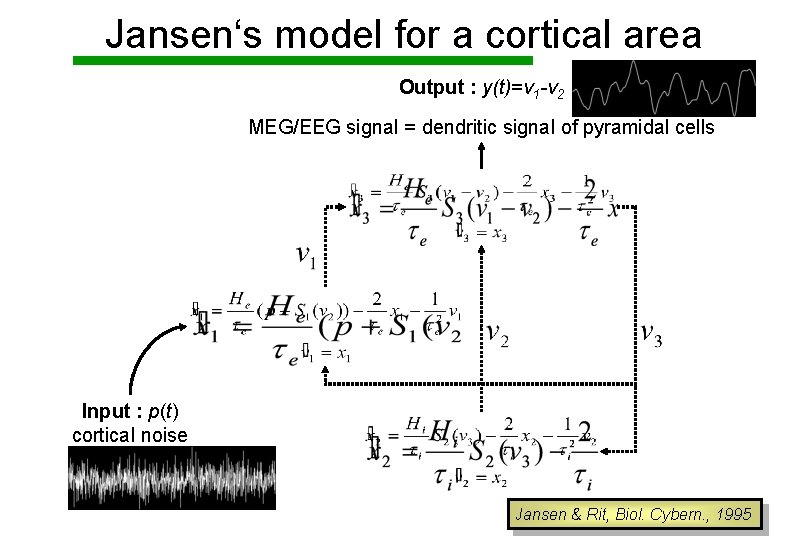
Jansen‘s model for a cortical area Output : y(t)=v 1 -v 2 MEG/EEG signal = dendritic signal of pyramidal cells Input : p(t) cortical noise Jansen & Rit, Biol. Cybern. , 1995

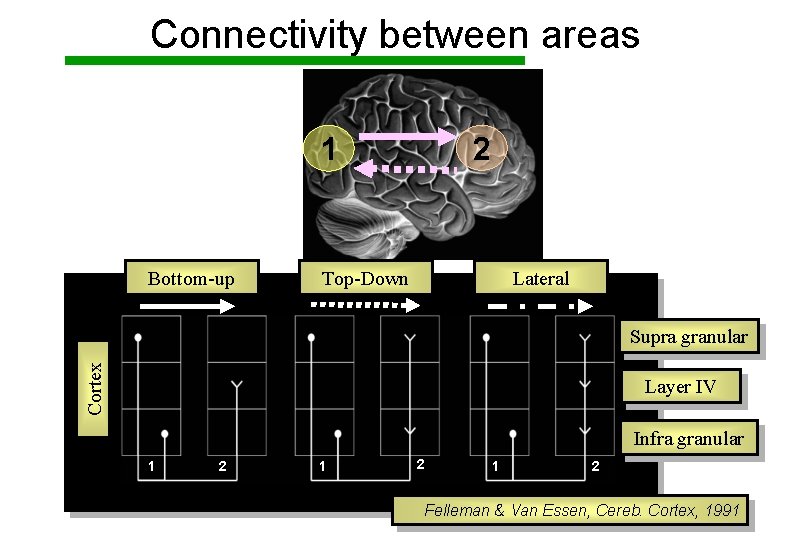
Connectivity between areas 2 1 Bottom-up Top-Down Lateral Cortex Supra granular Layer IV Infra granular 1 2 1 2 Felleman & Van Essen, Cereb. Cortex, 1991

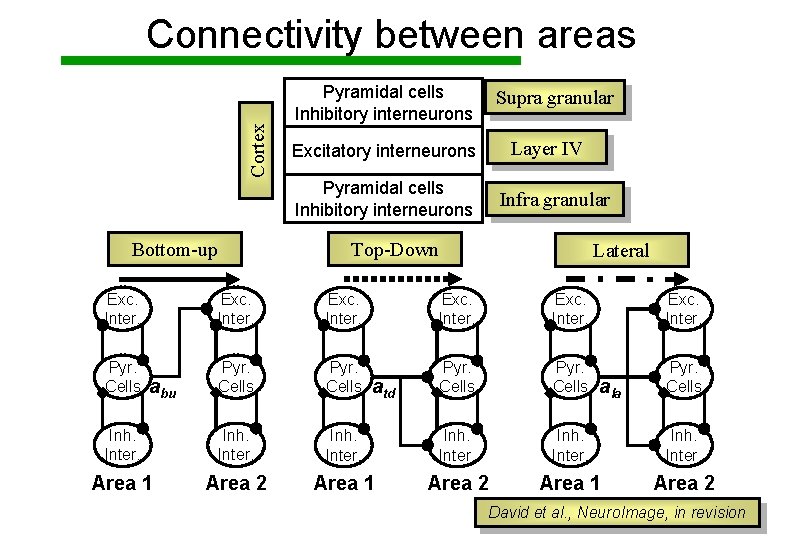
Cortex Connectivity between areas Pyramidal cells Inhibitory interneurons Supra granular Layer IV Excitatory interneurons Pyramidal cells Inhibitory interneurons Bottom-up Infra granular Top-Down Lateral Exc. Inter. Pyr. Cells Inh. Inter. Area 1 Area 2 abu atd ala David et al. , Neuro. Image, in revision

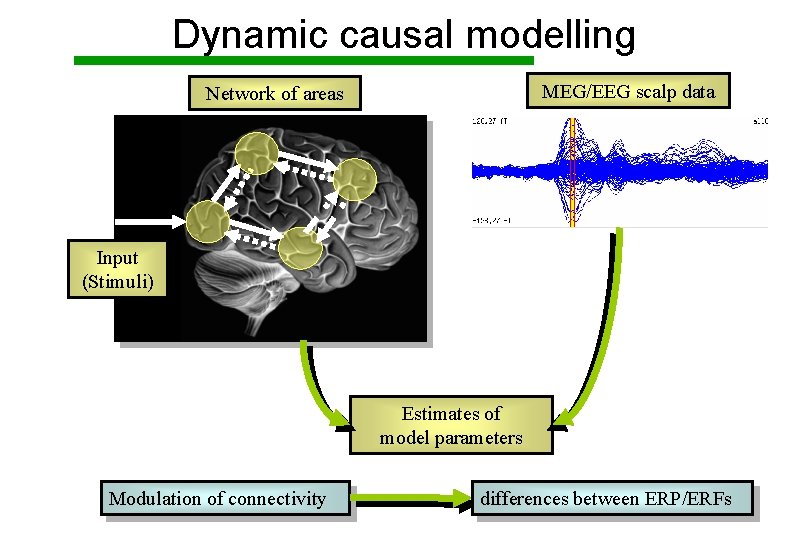
Dynamic causal modelling MEG/EEG scalp data Network of areas Input (Stimuli) Estimates of model parameters Modulation of connectivity differences between ERP/ERFs

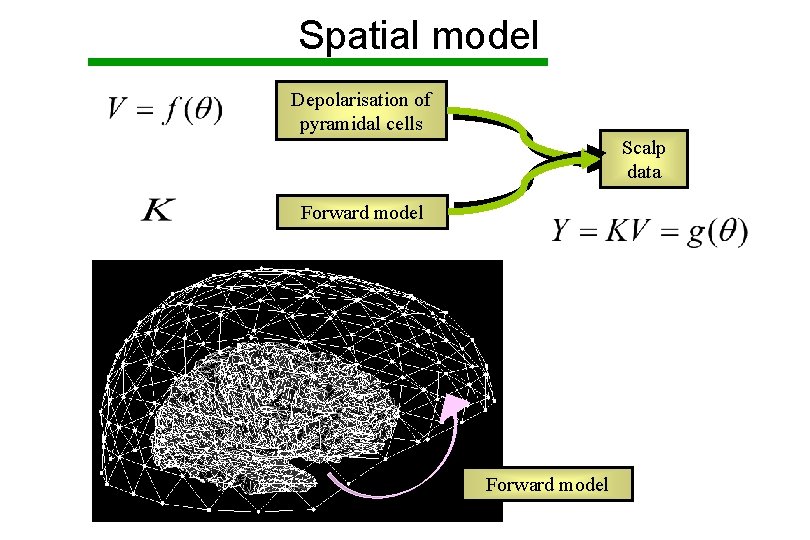
Spatial model Depolarisation of pyramidal cells Scalp data Forward model

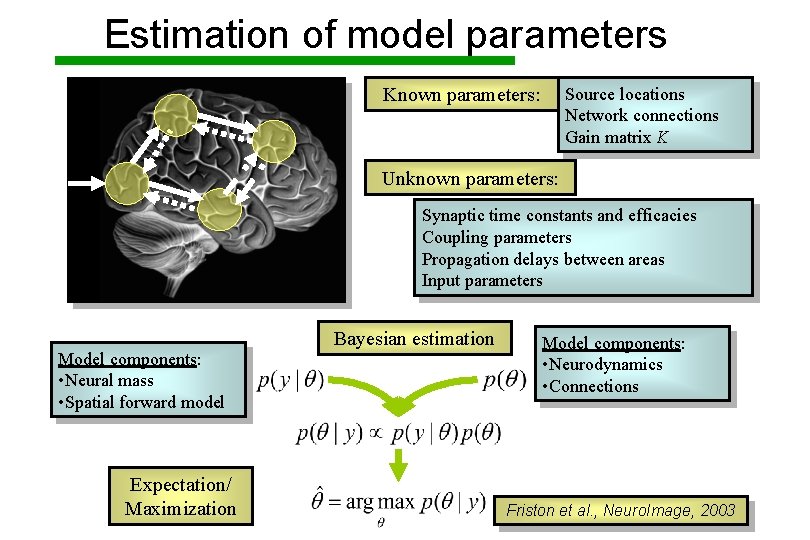
Estimation of model parameters Source locations Network connections Gain matrix K Known parameters: Unknown parameters: Synaptic time constants and efficacies Parameters Coupling parameters • Neurodynamics Propagation delays between areas • Connections (stability) Input parameters Model components: • Neural mass • Spatial forward model Expectation/ Maximization Bayesian estimation Model components: • Neurodynamics • Connections Friston et al. , Neuro. Image, 2003