STATS 730 Lectures 6 Exponential families Minimal sufficiency

STATS 730: Lectures 6 §Exponential families §Minimal sufficiency §Mean squared error §Unbiased estimation §Cramer-Rao lower bound 10/15/2021 730 Lectures 5&6 1

Exponential families n n n 10/15/2021 Mean is sufficient for normal, Poisson, exponential, … Is this a coincidence? No, all are special cases of the exponential family of distributions 730 Lectures 5&6 2

Exponential families (cont) These are joint distributions of the form Exp(C(q)S(x)+d(q)+B(x)) The range of X can’t depend on q. It is clear that S(x) is sufficient (why? ) 10/15/2021 730 Lectures 5&6 3

Exponential families (cont) Poisson, Normal, exponential are all members of this family. eg for the exponential, joint density is 10/15/2021 730 Lectures 5&6 4

Multiparameter exponential families n n n 10/15/2021 Sometimes q is a vector parameter, eg N(m, s 2), q=(m, s 2). Multiparameter exponential families are of the form Exp(SCi(q)Si(x) + d(q)+b(x)) Vector statistic (S 1(X), …, Sk(X)) is sufficient for q. Note dimensions of parameter and statistic don’t have to be the same. 730 Lectures 5&6 5

Example: Normal Take N(m, s 2), q=(m, s 2). Then the joint density is C 1(q) S 1(X) C 2(q) S 2(X) d(q) (S 1(X), S 2(X))=(SXi 2, SXi) is sufficient. 10/15/2021 730 Lectures 5&6 6

Minimal sufficiency Suppose X 1, . . , Xn are an iid sample from N(q, 1). Then (a) X 1, . . , Xn are sufficient (b) X(1), . . , X(n) are sufficient (c) Sample mean is sufficient (c) achieves the most “data reduction”. (c) is a function of (b) is a function of (a) 10/15/2021 730 Lectures 5&6 7

Minimal sufficiency n A “minimal sufficient” statistic achieves the most data reduction. A statistic is minimal sufficient if it is a function of every other sufficient statistic. 10/15/2021 730 Lectures 5&6 8

Minimal sufficiency(cont) n n 10/15/2021 Its hard to recognise minimal sufficient statistics using the definition. Here is a theorem that is more useful. See the notes p 23. The proof is not examinable. 730 Lectures 5&6 9

Minimal sufficiency theorem A statistic S is minimal sufficient if it has the following property: S(x)=S(y) iff f(x, q)/f(y, q) does not depend on q 10/15/2021 730 Lectures 5&6 10

Example n Poisson: This does not depend on q iff Thus the sample mean is minimal sufficient. 10/15/2021 730 Lectures 5&6 11

Small bias and standard error n n 10/15/2021 Now we return to the ideas of bias and small standard error, and connect them with sufficiency Recall that we want bias to be small and standard error small. Wee can combine these in the idea of mean squared error: 730 Lectures 5&6 12

Mean squared error Defined as Can be written as 10/15/2021 730 Lectures 5&6 Zero! BIAS 13

Mean square error Ideally, we want estimators with smaller mse than any other for all q. But this is impossible! (why? ) 10/15/2021 730 Lectures 5&6 14

Mean squared error So either … pick an estimator that has smaller mse for likely values of q (Bayes estimator) or… pick an estimator that has smaller mse than a restricted set of estimators 10/15/2021 730 Lectures 5&6 15

Mean square error All estimators A restricted set 10/15/2021 730 Lectures 5&6 16

Mean square error Set we have in mind: Unbiased estimators All estimators of q Unbiased estimators of q 10/15/2021 730 Lectures 5&6 17

Unbiased estimators An estimator S is unbiased if the bias is zero: ie if E(S)=q. We want the unbiased estimator of q that has smallest MSE (same as smallest variance or standard error) This is called the UMVUE (uniformly minimum variance unbiased estimator) 10/15/2021 730 Lectures 5&6 18

Finding umvues n 10/15/2021 Find an estimate that attains the Cramer-Rao lower bound n Condition on suficient statistics n Use the MLE 730 Lectures 5&6 19

CR lower bound n If S is an unbiased estimate of q, then Joint density 10/15/2021 730 Lectures 5&6 20

CR lower bound n n 10/15/2021 U is the score function I is the information matrix q is a vector parameter Cov(S) ³ I(q)-1 means that the matrix Cov(S) - I(q)-1 is positive definite. 730 Lectures 5&6 21

CR lower bound n n 10/15/2021 Proof follows from the following steps: Step 1 730 Lectures 5&6 22

CR lower bound (cont) n Step 2: This is 0! 10/15/2021 730 Lectures 5&6 23

CR lower bound (cont) Step 3: Put T=(S, U) Then Cov(T)= is PD Thus Cov(T) -1 is PD Thus is PD • Thus Cov(S)-I(q) -1 is PD 10/15/2021 730 Lectures 5&6 24

Useful fact: 10/15/2021 730 Lectures 5&6 25

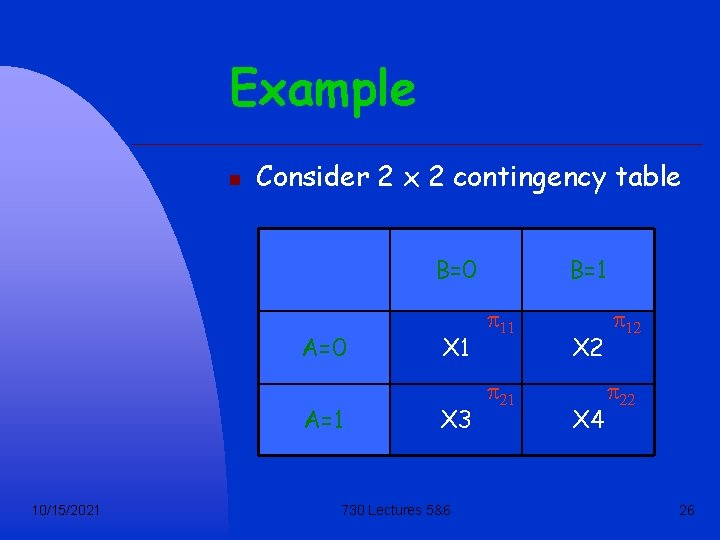
Example n Consider 2 x 2 contingency table B=0 A=1 10/15/2021 X 3 730 Lectures 5&6 B=1 p 11 p 21 X 2 X 4 p 12 p 22 26

Example(cont) Assume a multinomial probability model, with cell probabilities ie an independence model. 10/15/2021 730 Lectures 5&6 27

Example(cont) Log likelihood is ie an independence model. 10/15/2021 730 Lectures 5&6 28

Example(cont) Score is 10/15/2021 730 Lectures 5&6 29

Example(cont) Information is 10/15/2021 730 Lectures 5&6 30

Example(cont) Similarly Hence 10/15/2021 730 Lectures 5&6 31

Example(cont) Consider usual estimate Must be UMVUE!! 10/15/2021 730 Lectures 5&6 32