730 Lecture 14 Todays lecture 6182021 730 Lecture
























- Slides: 28

730 Lecture 14 Today’s lecture: 6/18/2021 730 Lecture 14 1

Confidence Intervals Two methods • Inverting tests • Finding pivotal quantities 6/18/2021 730 Lecture 14 2

Tests: revision • To test H 0: q=q 0 vs H 1: q¹q 0 Accept H 0 if XÎA(q 0) Acceptance region • Significance level & power: 6/18/2021 730 Lecture 14 3

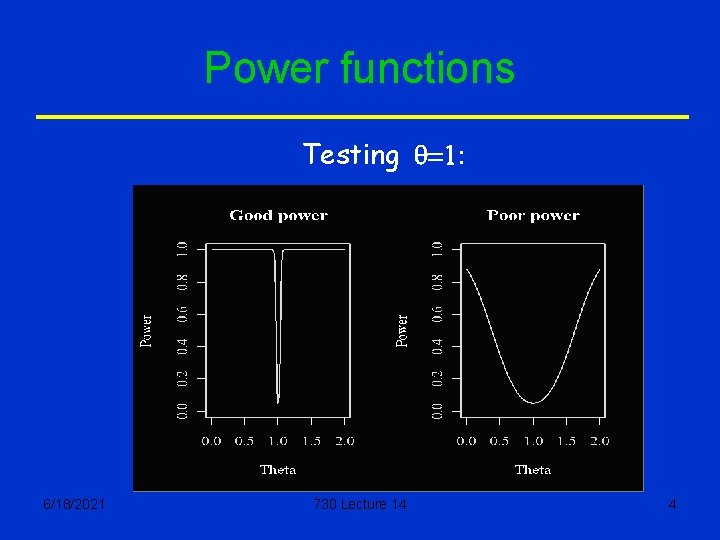
Power functions Testing q=1: 6/18/2021 730 Lecture 14 4

Confidence intervals • If L(X), R(X) are statistics such that P(L<q<R)=1 -a. . • then [L, R] is a 100(1 -a)% confidence interval for q with coverage probability 1 -a 6/18/2021 730 Lecture 14 5

Inverting tests • Consider an acceptance region A(q 0) • Let S(X) be the set of q 0 ‘s for which H 0: q = q 0 is accepted. Thus qÎ S(X) iff XÎA(q). Then • Often S is an interval so 6/18/2021 730 Lecture 14 6

Example 1 • Distribution: N(q, 1) • Hypothesis: H 0: q = q 0 6/18/2021 730 Lecture 14 7

Example 2 • Distribution: N(m, s 2) • Hypothesis: H 0: m = m 0 6/18/2021 730 Lecture 14 8

Example 3 • Distribution: N(m, s 2) • Hypothesis: H 0: s = s 0 6/18/2021 730 Lecture 14 9

Example 4 • Distribution: Bin(n, p) • Hypothesis: H 0: p = p 0 • “Wald test” 6/18/2021 730 Lecture 14 10

Example 5 • Distribution: Bin(n, p) • Hypothesis: H 0: p = p 0 • “Score test” 6/18/2021 730 Lecture 14 11

Example 5(cont) • Roots: 6/18/2021 730 Lecture 14 12

Example 6 Distribution: Bin(n, p) Hypothesis: H 0: p = p 0 “Exact test” Put x. L=largest integer such that Put x. R=smallest integer such that 6/18/2021 730 Lecture 14 13

Example 6 (cont) A “conservative” test 6/18/2021 730 Lecture 14 14

Inverting Useful facts (prove by integration by parts) F 1: df of Beta(n-x, x+1) F 2: df of Beta(x, n-x+1) 6/18/2021 730 Lecture 14 15

Inverting (cont) 6/18/2021 730 Lecture 14 16

Inverting (cont) 6/18/2021 730 Lecture 14 17

Using pivotal quantities • A pivotal quantity is a function S(X, q) of the data X and the parameters q whose distribution does not depend on q. • We invert the pivot to get the interval. 6/18/2021 730 Lecture 14 18

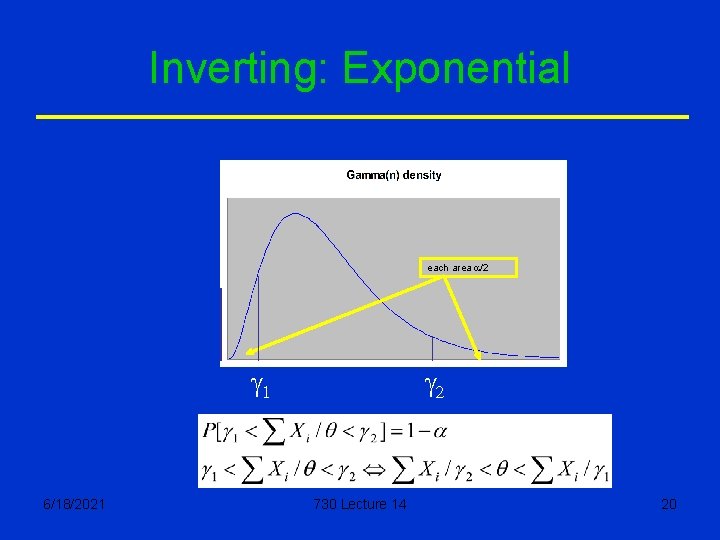
Examples • Normal N(q, 1). See Example 1 • Normal N(m, s 2). See Examples 2&3 • Exponential with mean q: SXi/ q is Gamma(n) 6/18/2021 730 Lecture 14 19

Inverting: Exponential each area a/2 g 1 6/18/2021 g 2 730 Lecture 14 20

Approximate pivots 6/18/2021 730 Lecture 14 21

Binomial distribution 6/18/2021 730 Lecture 14 22

Exponential distribution 6/18/2021 730 Lecture 14 23

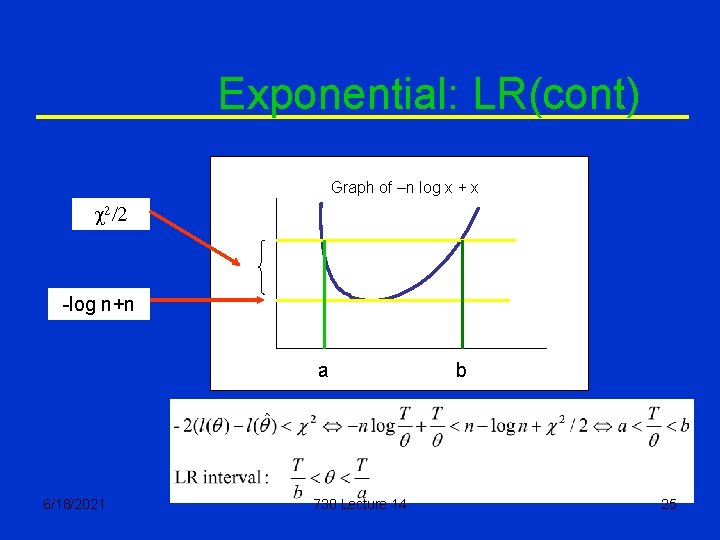
Exponential: Using the LR pivot 6/18/2021 730 Lecture 14 24

Exponential: LR(cont) Graph of –n log x + x c 2/2 -log n+n a 6/18/2021 730 Lecture 14 b 25

Summary 6/18/2021 730 Lecture 14 26

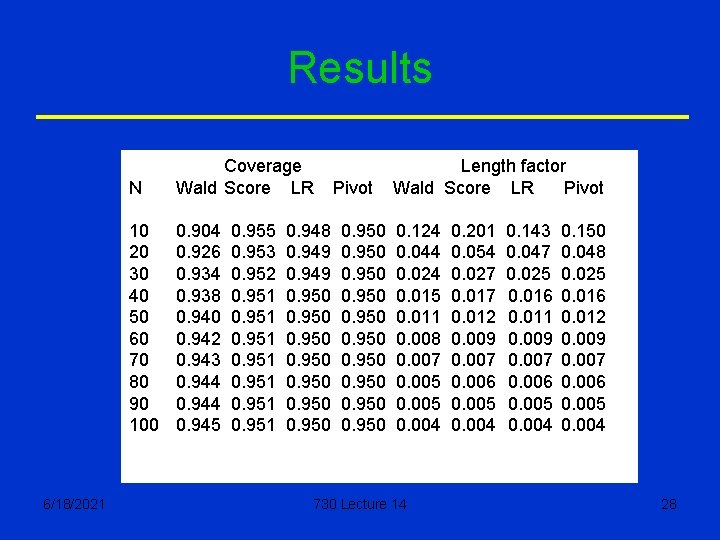
Comparison • All of form Compare in terms of “coverage” where G is DF of Gamma(n), and “Average length”, proportional to 1/A-1/B. 6/18/2021 730 Lecture 14 27

Results 6/18/2021 N Coverage Wald Score LR 10 20 30 40 50 60 70 80 90 100 0. 904 0. 926 0. 934 0. 938 0. 940 0. 942 0. 943 0. 944 0. 945 0. 953 0. 952 0. 951 0. 948 0. 949 0. 950 0. 950 Pivot 0. 950 0. 950 Length factor Wald Score LR Pivot 0. 124 0. 044 0. 024 0. 015 0. 011 0. 008 0. 007 0. 005 0. 004 730 Lecture 14 0. 201 0. 054 0. 027 0. 012 0. 009 0. 007 0. 006 0. 005 0. 004 0. 143 0. 047 0. 025 0. 016 0. 011 0. 009 0. 007 0. 006 0. 005 0. 004 0. 150 0. 048 0. 025 0. 016 0. 012 0. 009 0. 007 0. 006 0. 005 0. 004 28
 Sps 730
Sps 730 Arlon 25fr
Arlon 25fr 725 en yakın yüzlüğe yuvarlama
725 en yakın yüzlüğe yuvarlama Ars 28-730
Ars 28-730 Ieee 730
Ieee 730 730-170
730-170 Planetarypositionstoday
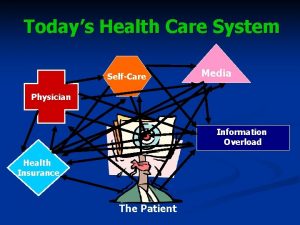
Planetarypositionstoday Todays health
Todays health Cell jeopardy
Cell jeopardy Welcome to today's class
Welcome to today's class Todays with apostrophe
Todays with apostrophe Teacher good morning student
Teacher good morning student Todays weather hull
Todays weather hull Todays objective
Todays objective Todays whether
Todays whether Todays wordlw
Todays wordlw Todays sabbath lesson
Todays sabbath lesson Whats todays temperature
Whats todays temperature Todays objective
Todays objective Todays class
Todays class Objective in resume for job
Objective in resume for job Mla title page
Mla title page Todays objective
Todays objective Todays objective
Todays objective Stuttering jeopardy game
Stuttering jeopardy game Todays worldld
Todays worldld Adam smith jeopardy
Adam smith jeopardy Conclusion of digestive system
Conclusion of digestive system Todays vision
Todays vision