SPM 2002 A priori complicated a posteriori very

SPM 2002 A priori complicated … a posteriori very simple ! C 2 C 1 C 2^ C 3^ C 1 PC ^ Xb 3 1 C C 2 Xb Space of X C 3^ C 1 X = C 3 ^ C 1 ) ( C 2 C 1 X’Y = b = (X’X) C P X Xb ace Sp ^ Xb -3 C 1 Xb Xb ^ 2 L C 1 Y/S 1 C 2 C 1 C 2 C 3 C 12 CC 2 C 3^ 2 Y/S 2 LC 1^ Y e LC 2 LC 1 Space of X Xb C 2 P ^ Xb C 1 ^ ^ C 2 X b C 2^C 3 ^ ^ Space of X Jean-Baptiste Poline Orsay SHFJ-CEA

SPM course - 2002 LINEAR MODELS and CONTRASTS T and F tests : (orthogonal projections) Hammering a Linear Model The RFT Use for Normalisation Jean-Baptiste Poline Orsay SHFJ-CEA www. madic. org

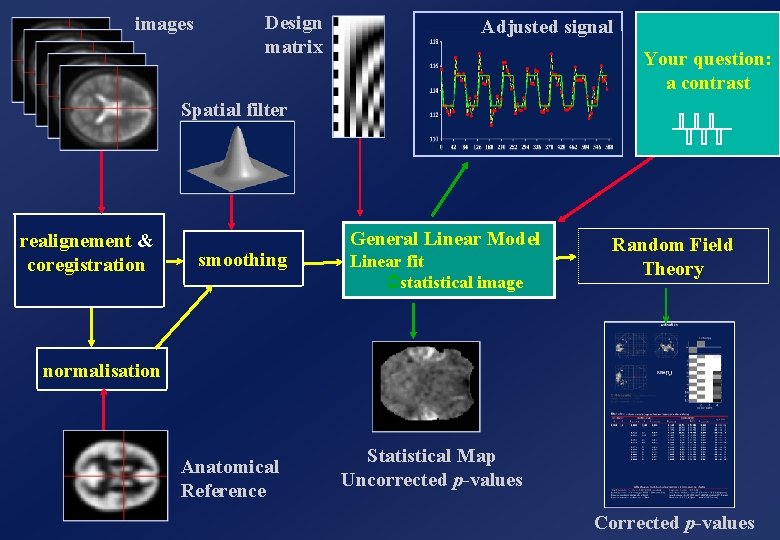
images Design matrix Adjusted signal Your question: a contrast Spatial filter realignement & coregistration smoothing General Linear Model Linear fit Ü statistical image Random Field Theory normalisation Anatomical Reference Statistical Map Uncorrected p-values Corrected p-values

Plan w Make sure we know all about the estimation (fitting) part. . w Make sure we understand the testing procedures : t and F tests w A bad model. . . And a better one w Correlation in our model : do we mind ? w A (nearly) real example

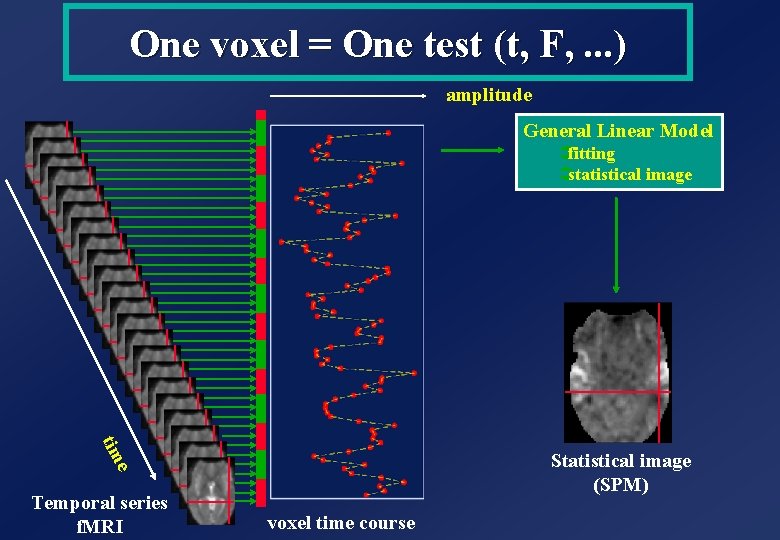
One voxel = One test (t, F, . . . ) amplitude General Linear Model Üfitting Üstatistical image tim e Statistical image (SPM) Temporal series f. MRI voxel time course

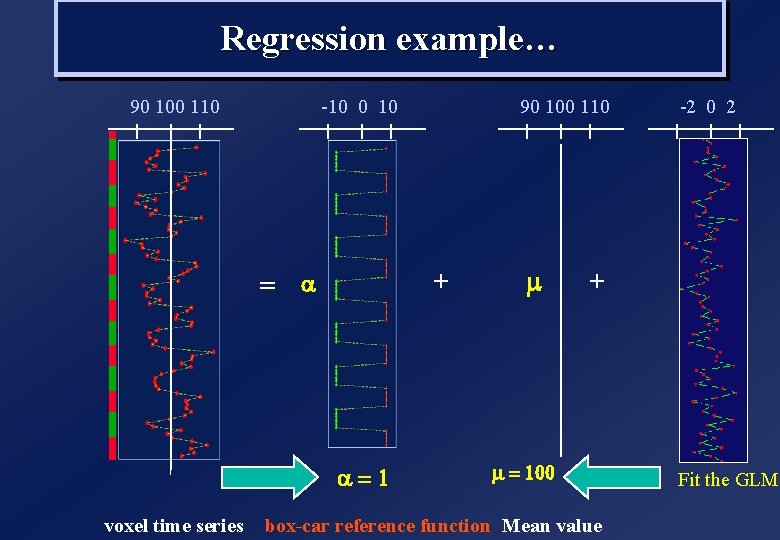
Regression example… 90 100 110 -10 0 10 + = a a=1 voxel time series 90 100 110 m -2 0 2 + m = 100 box-car reference function Mean value Fit the GLM

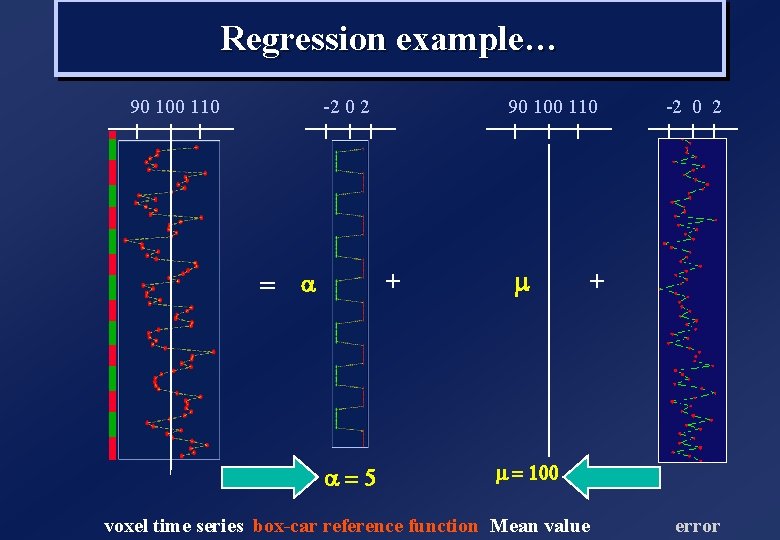
Regression example… 90 100 110 -2 0 2 + = a a=5 m -2 0 2 + m = 100 voxel time series box-car reference function Mean value error

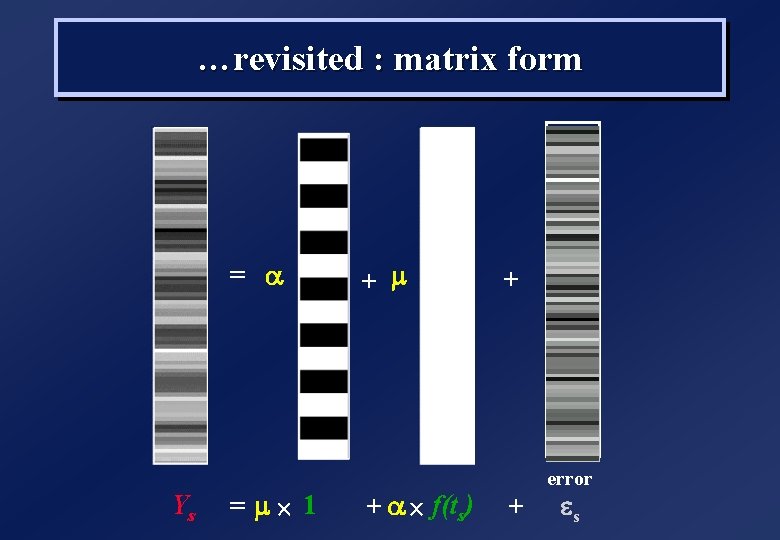
…revisited : matrix form = a Ys = m´ 1 + m + a ´ f(ts) + error + es

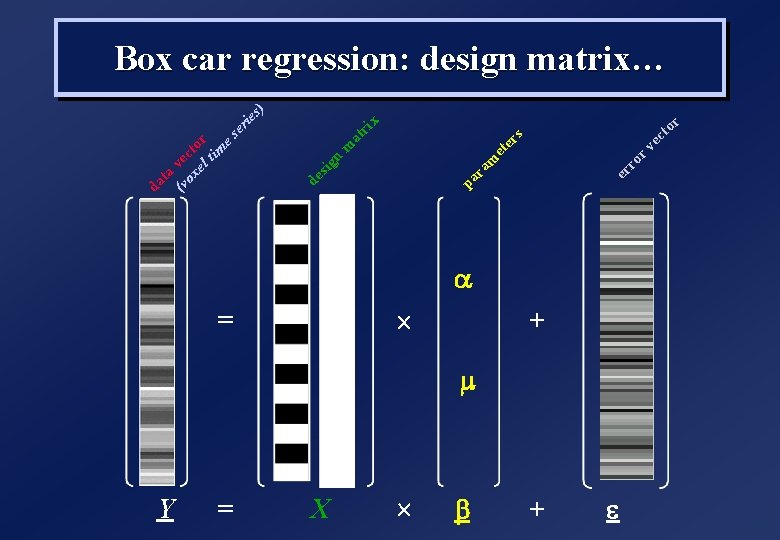
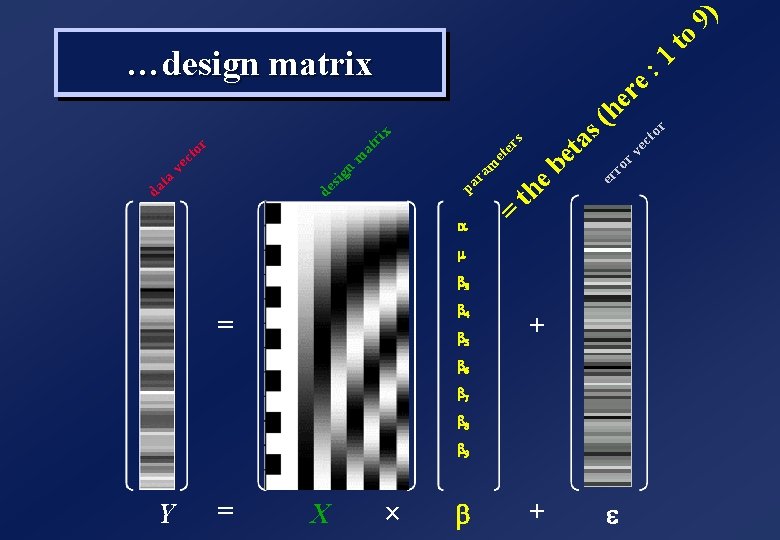
Y = = X ´ ´ b r to ec r v ro er s x er ie ri at er et m ra pa m n de sig (v vec ox to el r tim es ta da s) Box car regression: design matrix… a + m + e

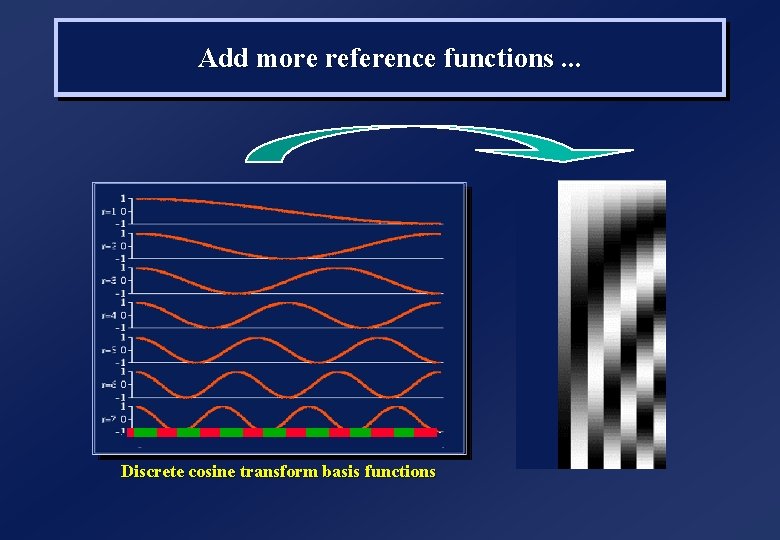
Add more reference functions. . . Discrete cosine transform basis functions

Y = X a = b 4 b 5 ´ b s er et ri x + 1 he r v re ec : to r ro er s ( e b et a th = m ra pa at n m de sig r to ec v ta da ) to 9 …design matrix m b 3 + b 6 b 7 b 8 b 9 e

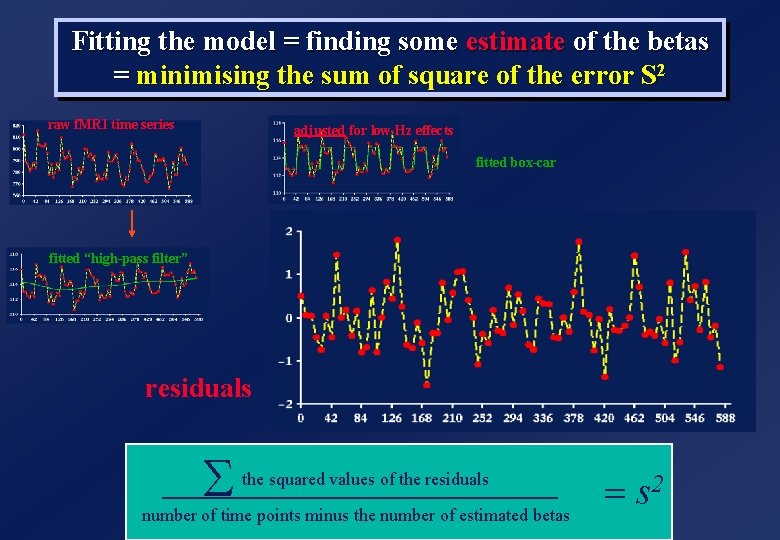
Fitting the model = finding some estimate of the betas = minimising the sum of square of the error S 2 raw f. MRI time series adjusted for low Hz effects fitted box-car fitted “high-pass filter” residuals S the squared values of the residuals number of time points minus the number of estimated betas = s 2

Summary. . . w We put in our model regressors (or covariates) that represent how we think the signal is varying (of interest and of no interest alike) w Coefficients (=estimated parameters or betas) are found such that the sum of the weighted regressors is as close as possible to our data w As close as possible = such that the sum of square of the residuals is minimal w These estimated parameters (the “betas”) depend on the scaling of the regressors : keep in mind when comparing ! w The residuals, their sum of square, the tests (t, F), do not depend on the scaling of the regressors

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w A bad model. . . And a better one w Correlation in our model : do we mind ? w A (nearly) real example

T test - one dimensional contrasts - SPM{t} A contrast = a linear combination of parameters: c´ ´ b c’ = 1 0 0 0 0 box-car amplitude > 0 ? = b 1 > 0 ? (b 1 : estimation of b 1 ) = b 1 b 2 b 3 b 4 b 5. . 1 xb 1 + 0 xb 2 + 0 xb 3 + 0 xb 4 + 0 xb 5 +. . . > 0 ? = test H 0 : c´ ´ b > 0 ? T = contrast of estimated parameters variance estimate c’b T = s 2 c’(X’X)+c SPM{t}

^ b How is this computed ? (t-test) contrast of estimated parameters variance estimate Estimation [Y, X] [b, s] Y = X b + e e ~ s 2 N(0, I) (Y : at one position) b = (X’X)+ X’Y (b = estimation of b) -> beta? ? ? images e = Y - Xb (e = estimation of e) s 2 = (e’e/(n - p)) (s = estimation of s, n: temps, p: paramètres) -> 1 image Res. MS 2 Test [b, s , c] [c’b, t] Var(c’b) = s 2 c’(X’X)+c (compute for each contrast c) t = c’b / sqrt(s 2 c’(X’X)+c) (c’b -> images spm_con? ? ? compute the t images -> images spm_t? ? ? ) under the null hypothesis H 0 : t ~ Student( df ) df = n-p

F test (SPM{F}) : a reduced model or. . . Tests multiple linear hypotheses : Does X 1 model anything ? H 0: True model is X 0 X 0 X 1 additional variance accounted for by tested effects S 2 This model ? S 02 > S 2 Or this one ? F = error variance estimate F ~ ( S 02 - S 2 ) / S 2

F test (SPM{F}) : a reduced model or. . . multi-dimensional contrasts ? tests multiple linear hypotheses. Ex : does HPF model anything? H 0: True model is X 0 X 1 (b 3 -9) H 0: b 3 -9 = (0 0 0 0. . . ) X 0 test H 0 : c´ ´ b = 0 ? 0 0 1 0 0 c’ = 0 0 0 0 1 0 0 0 0 1 c’ = +1 0 0 0 0 SPM{F} This model ? Or this one ?

^2 s How is this computed ? (F-test) Estimation [Y, X] [b, s] additional variance accounted for by tested effects Error variance estimate Y = X b + e e ~ N(0, s 2 I) Y = X 0 b 0 + e 0 e 0 ~ N(0, s 02 I) X 0 : X Reduced Estimation [Y, X ] [b , s ] (not really like that ) b = (X ’X )+ X ’Y 0 0 0 0 e 0 = Y - X 0 b 0 (eà = estimation of eà) s 20 = (e 0’e 0/(n - p 0)) (sà = estimation of sà, n: time, pà: parameters) Test [b, s, c] [ess, F] F = (e 0’e 0 - e’e)/(p - p 0) / s 2 -> image (e 0’e 0 - e’e)/(p - p 0) : spm_ess? ? ? -> image of F : spm_F? ? ? under the null hypothesis : F ~ F(df 1, df 2) p - p 0 n-p

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w A bad model. . . And a better one w Correlation in our model : do we mind ? w A (nearly) real example

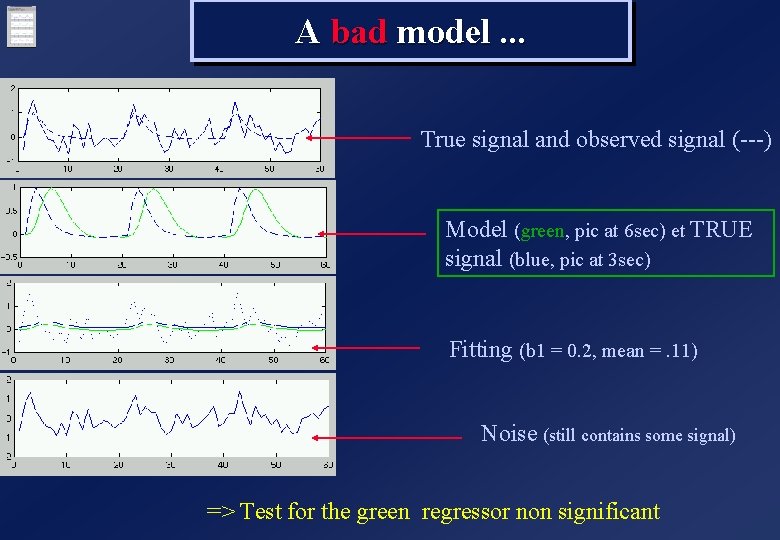
A bad model. . . True signal and observed signal (---) Model (green, pic at 6 sec) et TRUE signal (blue, pic at 3 sec) Fitting (b 1 = 0. 2, mean =. 11) Noise (still contains some signal) => Test for the green regressor non significant

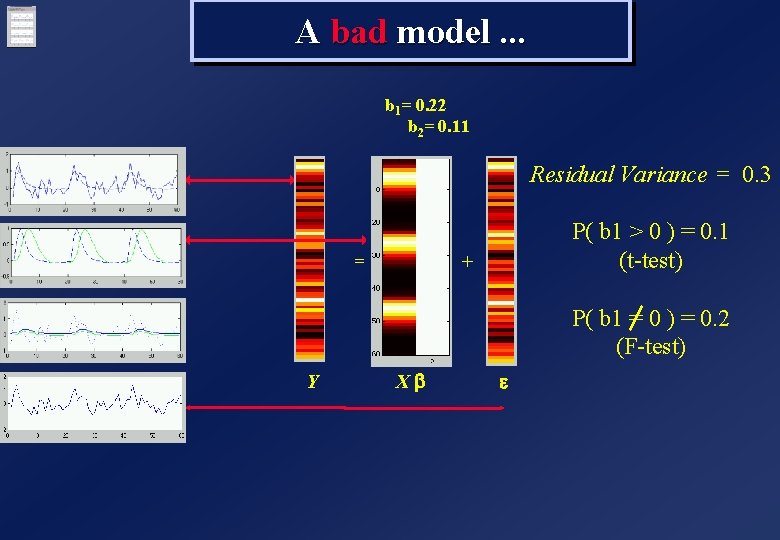
A bad model. . . b 1= 0. 22 b 2= 0. 11 Residual Variance = 0. 3 = P( b 1 > 0 ) = 0. 1 (t-test) + P( b 1 = 0 ) = 0. 2 (F-test) Y Xb e

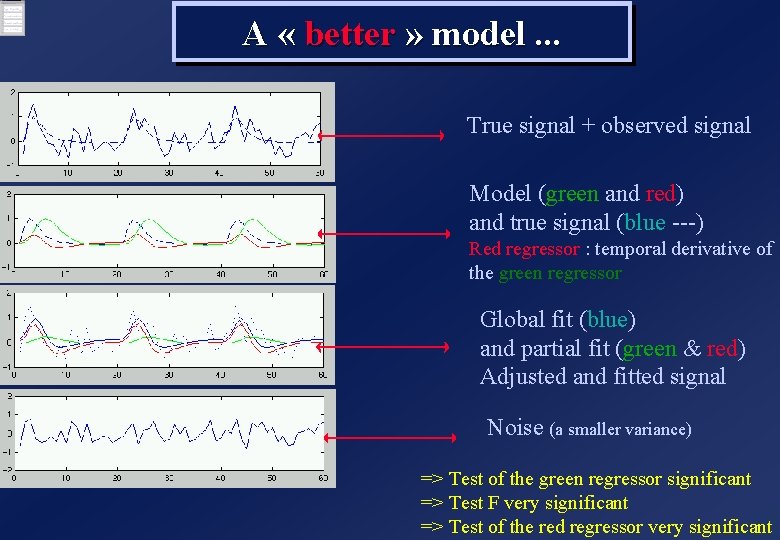
A « better » model. . . True signal + observed signal Model (green and red) and true signal (blue ---) Red regressor : temporal derivative of the green regressor Global fit (blue) and partial fit (green & red) Adjusted and fitted signal Noise (a smaller variance) => Test of the green regressor significant => Test F very significant => Test of the red regressor very significant

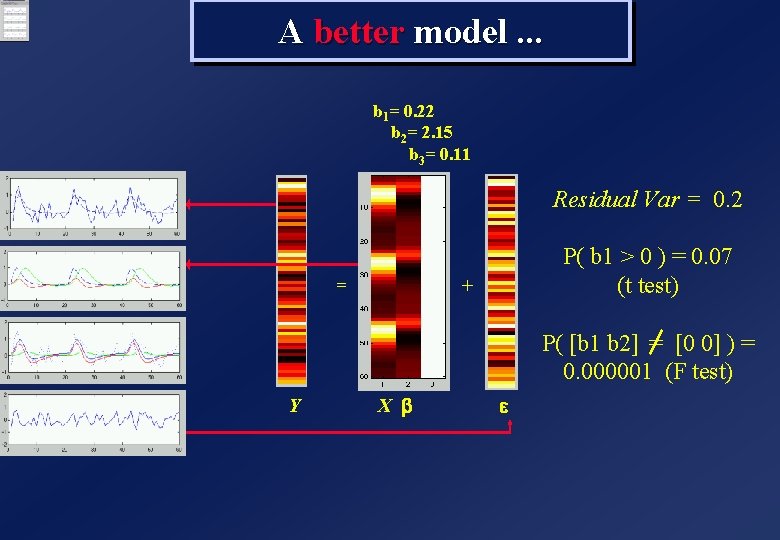
A better model. . . b 1= 0. 22 b 2= 2. 15 b 3= 0. 11 Residual Var = 0. 2 = P( b 1 > 0 ) = 0. 07 (t test) + P( [b 1 b 2] [0 0] ) = = 0. 000001 (F test) Y X b e

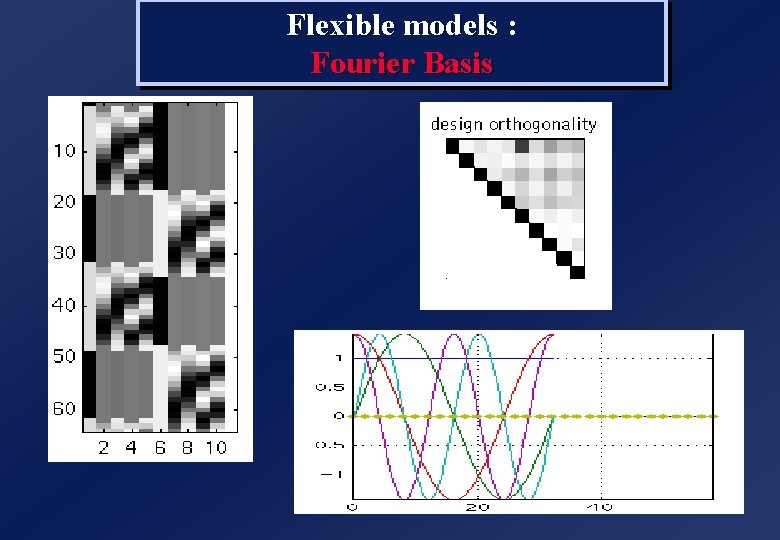
Flexible models : Fourier Basis

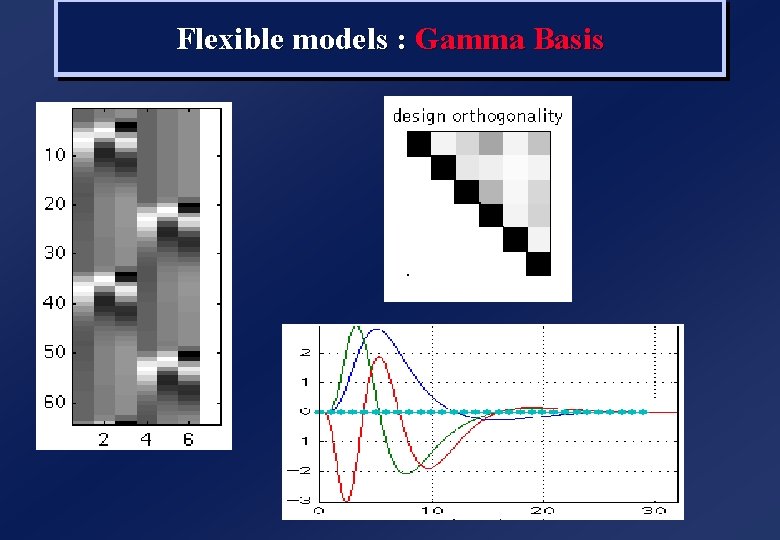
Flexible models : Gamma Basis

Summary. . . (2) w The residuals should be looked at. . . (non random structure ? ) w We rather test flexible models if there is little a priori information, and precise ones with a lot a priori information w In general, use the F-tests to look for an overall effect, then look at the betas or the adjusted signal to characterise the origin of the signal w Interpreting the test on a single parameter (one function) can be very confusing: cf the delay or magnitude situation

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w A bad model. . . And a better one w Correlation in our model : do we mind ? w A (nearly) real example ?

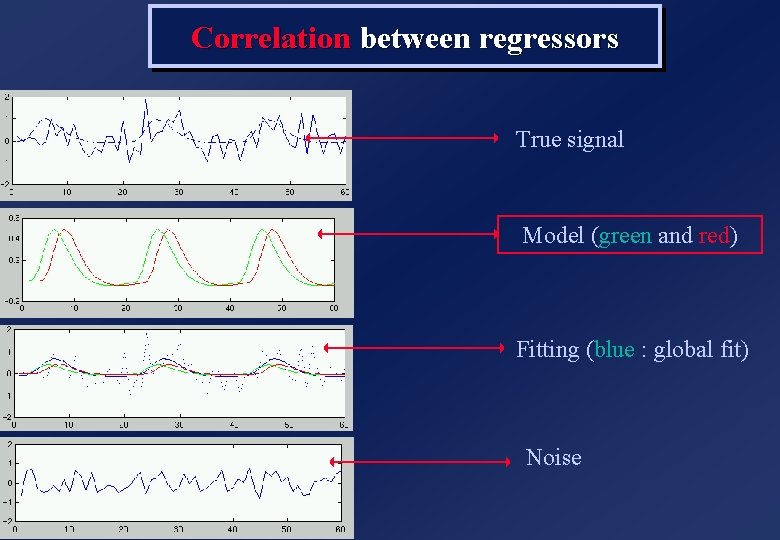
Correlation between regressors True signal Model (green and red) Fitting (blue : global fit) Noise

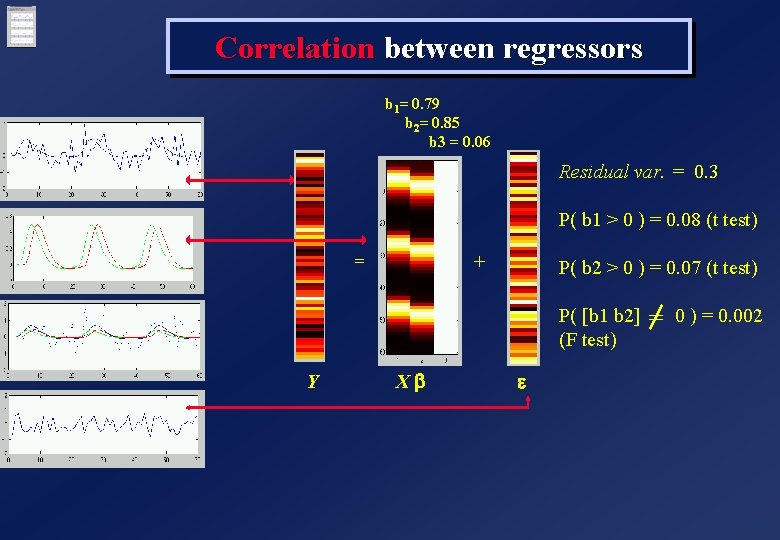
Correlation between regressors b 1= 0. 79 b 2= 0. 85 b 3 = 0. 06 Residual var. = 0. 3 P( b 1 > 0 ) = 0. 08 (t test) = + P( b 2 > 0 ) = 0. 07 (t test) P( [b 1 b 2] 0 ) = 0. 002 = (F test) Y Xb e

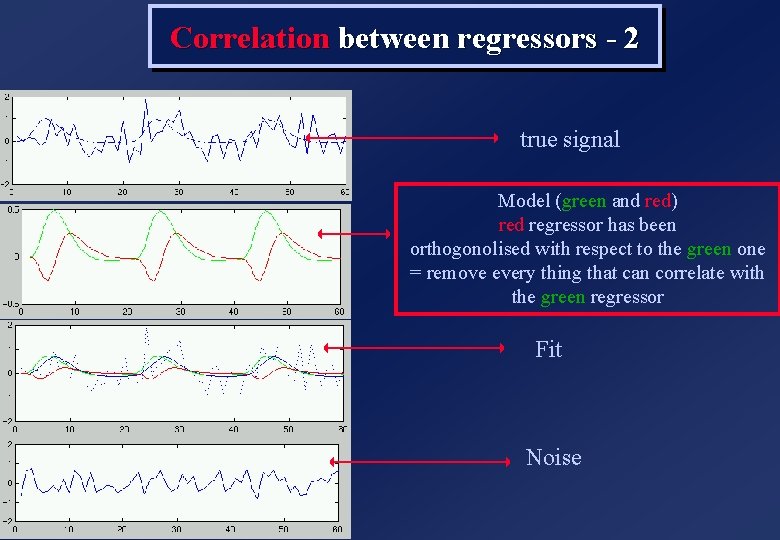
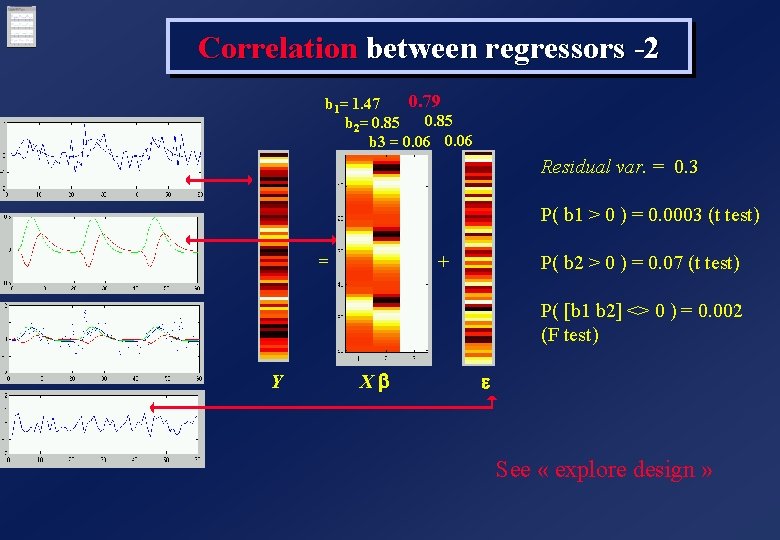
Correlation between regressors - 2 true signal Model (green and red) red regressor has been orthogonolised with respect to the green one = remove every thing that can correlate with the green regressor Fit Noise

Correlation between regressors -2 0. 79 b 1= 1. 47 b 2= 0. 85 0. 06 b 3 = 0. 06 Residual var. = 0. 3 P( b 1 > 0 ) = 0. 0003 (t test) = + P( b 2 > 0 ) = 0. 07 (t test) P( [b 1 b 2] <> 0 ) = 0. 002 (F test) Y Xb e See « explore design »

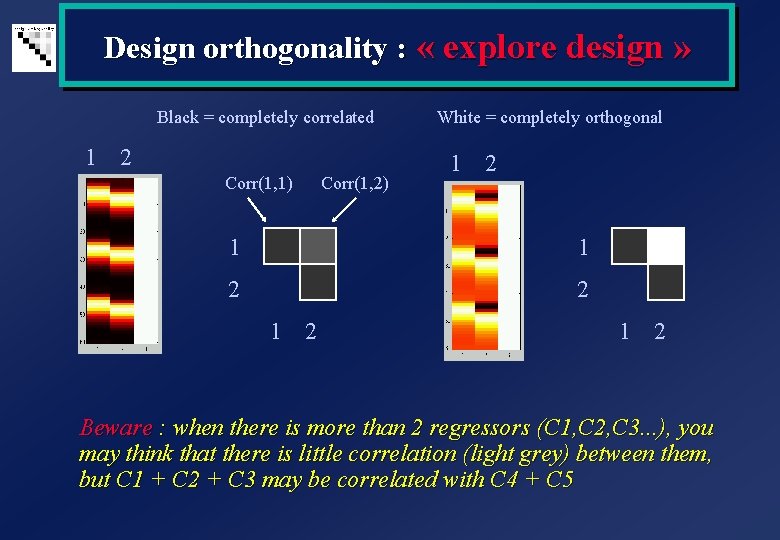
Design orthogonality : « explore design » Black = completely correlated White = completely orthogonal 1 2 Corr(1, 1) Corr(1, 2) 1 2 1 1 2 2 1 2 Beware : when there is more than 2 regressors (C 1, C 2, C 3. . . ), you may think that there is little correlation (light grey) between them, but C 1 + C 2 + C 3 may be correlated with C 4 + C 5

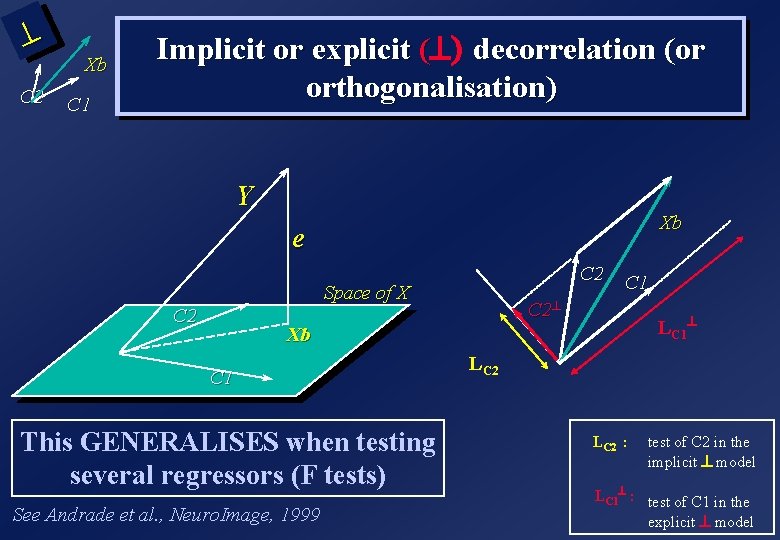
^ C 2 Xb C 1 Implicit or explicit (^) decorrelation (or orthogonalisation) Y Xb e C 2 Space of X C 2 C 1 C 2^ LC 1^ Xb C 1 This GENERALISES when testing several regressors (F tests) See Andrade et al. , Neuro. Image, 1999 LC 2 : test of C 2 in the implicit ^ model LC 1^ : test of C 1 in the explicit ^ model

^ ? b “completely” correlated. . . Y = Xb + e X = 1 0 1 0 1 1 Cond 2 Mean = C 1+C 2 C 1 Parameters are not unique in general ! Some contrasts have no meaning: NON ESTIMABLE Example here : c’ = [1 0 0] is not estimable ( = no specific information in the first regressor); c’ = [1 -1 0] is estimable;

Summary. . . (3) w We are implicitly testing additional effect only, so we may miss the signal if there is some correlation in the model using t tests w Orthogonalisation is not generally needed - parameters and test on the changed regressor don’t change w It is always simpler (when possible !) to have orthogonal (uncorrelated) regressors w In case of correlation, use F-tests to see the overall significance. There is generally no way to decide where the « common » part shared by two regressors should be attributed to w In case of correlation and you need to orthogonolise a part of the design matrix, there is no need to re-fit a new model : the contrast only should change.

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w A bad model. . . And a better one w Correlation in our model : do we mind ? w A (nearly) real example

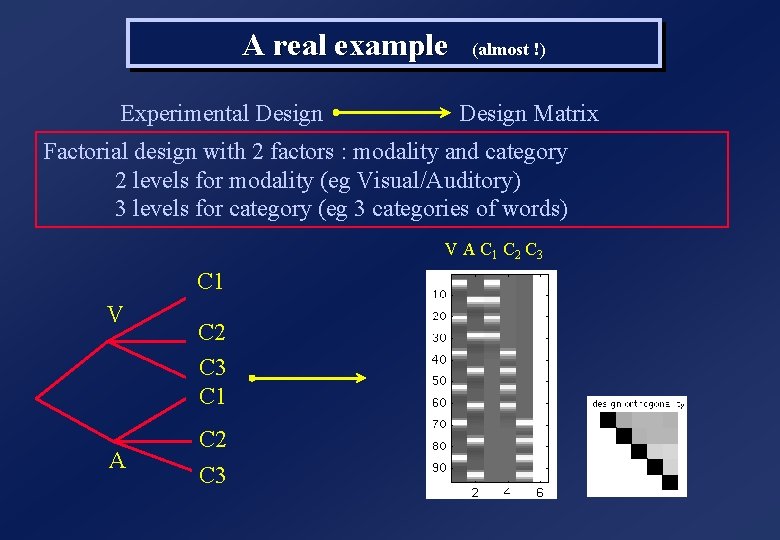
A real example (almost !) Experimental Design Matrix Factorial design with 2 factors : modality and category 2 levels for modality (eg Visual/Auditory) 3 levels for category (eg 3 categories of words) V A C 1 C 2 C 3 C 1 V A C 2 C 3 C 1 C 2 C 3

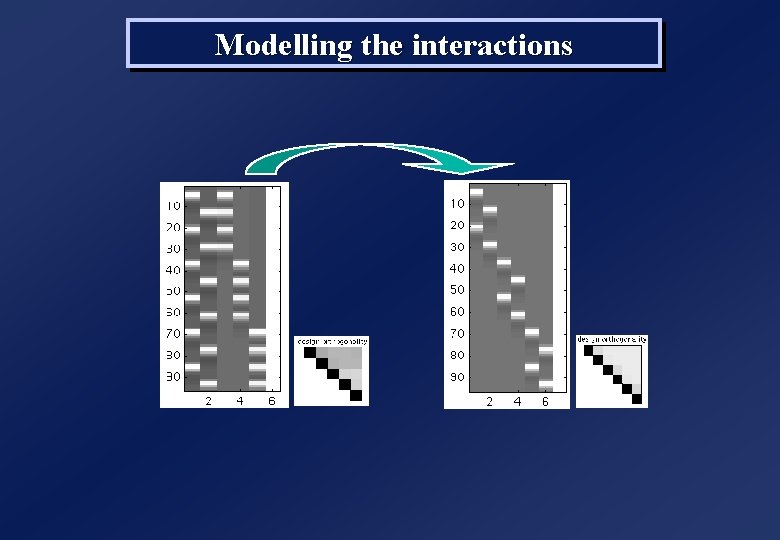
Asking ouselves some questions. . . V A C 1 C 2 C 3 2 ways : 1 - write a contrast c and test c’b = 0 2 - select colons of X for the model under the null hypothesis. The contrast manager allows that Test C 1 > C 2 : c = [ 0 0 1 -1 0 0 ] Test V > A : c = [ 1 -1 0 0 ] Test the modality factor : c = ? Use 2 Test the category factor : c = ? Use 2 Test the interaction Mx. C ? • Design Matrix not orthogonal • Many contrasts are non estimable • Interactions Mx. C are not modeled

Modelling the interactions

Asking ouselves some questions. . . C 1 C 2 C 3 V A V A Test C 1 > C 2 : c = [ 1 1 -1 -1 0 0 0] Test V > A : c = [ 1 -1 0] Test the differences between categories : [ 1 1 -1 -1 0 0 0] c = [ 0 0 1 1 -1 -1 0] Test everything in the category factor , leaves out modality : [ 1 1 0 0 0] c = [ 0 0 1 1 0 0 0] [ 0 0 1 1 0] Test the interaction Mx. C ? : [ 1 -1 -1 1 0 0 0] c = [ 0 0 1 -1 -1 1 0] [ 1 -1 0 0 -1 1 0] • Design Matrix orthogonal • All contrasts are estimable • Interactions Mx. C modelled • If no interaction. . . ? Model too “big”

Asking ouselves some questions. . . With a more flexible model C 1 C 2 C 3 V A V A Test C 1 > C 2 ? Test C 1 different from C 2 ? from c = [ 1 1 -1 -1 0 0 0] to c = [ 1 0 -1 0 0 0 0] [ 0 1 0 -1 0 0 0] becomes an F test! Test V > A ? c = [ 1 0 -1 0 0] is possible, but is OK only if the regressors coding for the delay are all equal

SPM course - 2002 LINEAR MODELS and CONTRASTS T and F tests : (orthogonal projections) Hammering a Linear Model The RFT We don’t use that one Use for Normalisation Jean-Baptiste Poline Orsay SHFJ-CEA www. madic. org