A PRIORI OR PLANNED CONTRASTS MULTIPLE COMPARISON TESTS

A PRIORI OR PLANNED CONTRASTS MULTIPLE COMPARISON TESTS

ANOVA �ANOVA is used to compare means. �However, if a difference is detected, and more than two means are being compared, ANOVA cannot tell you where the difference lies. �In order to figure out which means differ, you can do a series of tests: Planned or unplanned comparisons of means.

PLANNED or A PRIORI CONTRASTS �A comparison between means identified as being of utmost interest during the design of a study, prior to data collection. �You can only do one or a very small number of planned comparisons, otherwise you risk inflating the Type 1 error rate. �You do not need to perform an ANOVA first.

UNPLANNED or A POSTERIORI CONTRASTS �A form of “data dredging” or “data snooping”, where you may perform comparisons between all potential pairs of means in order to figure out where the difference(s) lie. �No prior justification for comparisons. �Increased risk of committing a Type 1 error. �The probability of making at least one type 1 error is not greater than α= 0. 05.

PLANNED ORTHOGONAL AND NON-ORTHOGONAL CONTRASTS �Planned comparisons may be orthogonal or non-orthogonal. �Orthogonal: mutually non-redundant and uncorrelated contrasts (i. e. : independent). �Non-Orthogonal: Not independent. �For example: 4 means: Y 1 , Y 2, Y 3, and Y 4 Orthogonal: Y 1 - Y 2 and Y 3 - Y 4 Non-Orthogonal: Y 1 -Y 2 and Y 2 -Y 3

ORTHOGONAL CONTRASTS �Limited number of contrasts can be made, simultaneously. �Any set of contrasts may have k-1 number of contrasts.

ORTHOGONAL CONTRASTS �For Example: k=4 means. Therefore, you can make 3 (i. e. : 4 -1) orthogonal contrasts at once.

HOW DO YOU KNOW IF A SET OF CONTRASTS IS ORTHOGONAL? �∑cijci’j=0 where the c’s are the particular coefficients associated with each of the means and the i indicates the particular comparison to which you are referring. �Multiply all of the coefficients for each particular mean together across all comparisons. �Then add them up! �If that sum is equal to zero, then the comparisons that you have in your set may be considered orthogonal.

HOW DO YOU KNOW IF A SET OF CONTRASTS IS ORTHOGONAL? �For Example: Set c 1 1 ½ ½ 1 cijci’j ∑cijci’j Coefficients c 2 c 3 -1 1 ½ -½ -½ -½ Contrasts c 4 -1 -½ ½ Y 1 -Y 2 Y 3 -Y 4 (Y 1+Y 2)/2 –(Y 3+Y 4)/2 0 (c 1)Y 1 + (c 2)Y 2 = Y 1 – Y 2 Therefore c 1 = 1 and c 2 = -1 because (1)Y 1 + (-1)Y 2 = Y 1 -Y 2 (After Kirk 1982)

ORTHOGONAL CONTRASTS �There always k-1 non-redundant questions that can be answered. �An experimenter may not be interested in asking all of said questions, however.

PLANNED COMPARISONS USING A t STATISTIC �A planned comparison addresses the null hypothesis that all of your comparisons between means will be equal to zero. Ho=Y 1 -Y 2=0 Ho= Y 3 -Y 4=0 Ho= (Y 1+Y 2)/2 –(Y 3+Y 4)/2 �These types of hypotheses can be tested using a t statistic.

PLANNED COMPARISONS USING A t STATISTIC �Very similar to a two sample t-test, but the standard error is calculated differently. �Specifically, planned comparisons use the pooled sample variance (MSerror )based on all k groups (and the corresponding error degrees of freedom) rather than that based only on the two groups being compared. �This step increases precision and power.

PLANNED COMPARISONS USING A t STATISTIC �Evaluate just like any other t-test. �Look up the critical value for t in the same table. �If the absolute value of your calculated t statistic exceeds the critical value, the null hypothesis is rejected.

PLANNED COMPARISONS USING A t STATISTIC: NOTE �All of the t statistic calculations for all of the comparisons in a particular set will use the same MSerror. �Thus, the tests themselves are not statistically independent, even though the comparisons that you are making are. �However, it has been shown that, if you have a sufficiently large number of degrees of freedom (40+), this shouldn’t matter. (Norton and Bulgren, as cited by Kirk, 1982)

PLANNED COMPARISONS USING AN F STATISTIC �You can also use an F statistic for these tests, because t 2 = F. �Different books prefer different methods. �The book I liked most used the t statistic, so that’s what I’m going to use throughout. �SAS uses F, however.

CONFIDENCE INTERVALS FOR ORTHOGONAL CONTRASTS �A confidence interval is a way of expressing the precision of an estimate of a parameter. �Here, the parameter that we are estimating is the value of the particular contrast that we are making. �So, the actual value of the comparison (ψ) should be somewhere between the two extremes of the confidence interval.

CONFIDENCE INTERVALS FOR ORTHOGONAL CONTRASTS �The values at the extremes are the 95% confidence limits. �With them, you can say that you are 95% confident that the true value of the comparison lies between those two values. �If the confidence interval does not include zero, then you can conclude that the null hypothesis can be rejected.

ADVANTAGES OF USING CONFIDENCE INTERVALS �When the data are presented this way, it is possible for the experimenter to consider all possible null hypotheses – not just the one that states that the comparison in question will equal 0. �If any hypothesized value lies outside of the 95% confidence interval, it can be rejected.

CHOOSING A METHOD �Orthogonal tests can be done in either way. �Both methods make the same assumptions and are equally significant.

ASSUMPTIONS �Assumptions: The populations are approximately normally distributed. Their variances are homogenous. �The t statistic is relatively robust to violations of these assumptions when the number of observations for each sample are equal. �However, when the sample sizes are not equal, the t statistic is not robust to the heterogeneity of variances.

HOW TO DEAL WITH VIOLATIONS OF ASSUMPTIONS �When population variances are unequal, you can replace the pooled estimator of variance, MSerror, with individual variance estimators for the means that you are comparing. �There a number of possible procedures that can be used when the variance between populations is heterogeneous: Cochran and Cox Welch Dixon, Massey, Satterthwaite and Smith

TYPE I ERRORS AND ORTHOGONAL CONTRASTS �For C independent contrasts at some level of significance (α), the probability of making one or more Type 1 errors is equal to: 1 -(1 -α)C �As the number of independent tests increases, so does the probability of committing a Type 1 error. �This problem can be reduced (but not eliminated) by restricting the use of multiple t-tests to a priori orthogonal contrasts.

A PRIORI NON-ORTHOGONAL CONTRASTS �Contrasts of interest that ARE NOT independent. �In order to reduce the probability of making a Type 1 error, the significance level (α) is set for the whole family of comparisons that is being made, as opposed to for each individual comparison. �For Example: Entire value of α for all comparisons combined is 0. 05. The value for each individual comparison would thus be less than that.

WHEN DO YOU DO THESE? �When contrasts are planned in advance. �They are relatively few in number. � BUT the comparisons are non-orthogonal (they are not independent). �i. e. : When one wants to contrast a control group mean with experimental group means.

DUNN’S MULTIPLE COMPARISON PROCEDURE �A. K. A. : Bonferoni t procedure. �Involves splitting up the value of α among a set of planned contrasts in an additive way. �For example: Total α = 0. 05, for all contrasts. One is doing 2 contrasts. α for each contrast could be 0. 025, if we wanted to divide up the α equally.

DUNN’S MULTIPLE COMPARISON PROCEDURE �If the consequences of making a Type 1 error are not equally serious for all contrasts, then you may choose to divide α unequally across all of the possible comparisons in order to reflect that concern.

DUNN’S MULTIPLE COMPARISON PROCEDURE �This procedure also involves the calculation of a t statistic (t. D). �The calculation involved in finding t. D is identical to that for determining t for orthogonal tests:

DUNN’S MULTIPLE COMPARISON PROCEDURE �However, you use a different table in order to look up the critical value (t. Dα; C, v ). Your total α value (not the value per comparison). Number of comparisons (C). And v, the number of degrees of freedom.

DUNN’S MULTIPLE COMPARISON PROCEDURE: ONE-TAILED TESTS �The table also only shows the critical values for two-tailed tests. �However, you can determine the approximate value of t. Dα; C, v for a onetailed test by using the following equation: t. Dα; C, v ≈ zα/C + (z 3α/C + zα/C)/4(v-2) ▪ Where the value of zα/C can be looked up in yet another table (“Areas under the Standard Normal Distribution”).

DUNN’S MULTIPLE COMPARISON PROCEDURE �Instead of calculating t. D for all contrasts of interest, you can simply calculate the critical difference (ψD) that a particular comparison must exceed in order to be significant: ψD = t. Dα/2; C, v √(2 MSerror/n). �Then compare this critical difference value to the absolute values of the differences between the means that you compared. �If they exceed ψD, they are significant.

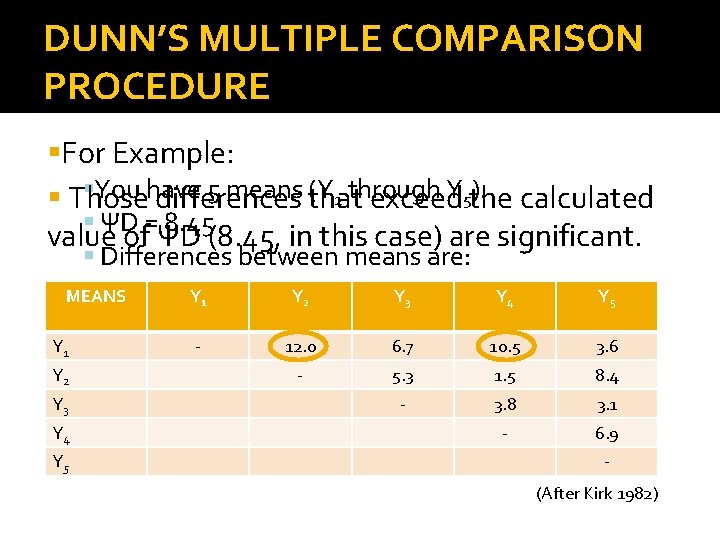
DUNN’S MULTIPLE COMPARISON PROCEDURE For Example: You have 5 means (Y 1 through Y 5). Those differences that exceed the calculated ΨD = 8. 45 value of ΨD (8. 45, in this case) are significant. Differences between means are: MEANS Y 1 Y 2 Y 3 Y 4 Y 5 - 12. 0 6. 7 10. 5 3. 6 - 5. 3 1. 5 8. 4 - 3. 8 3. 1 - 6. 9 (After Kirk 1982)

DUNN-SIDAK PROCEDURE �A modification of the Dunn procedure. t statistic (t. DS) and critical difference (ψDS). �There isn’t much difference between the two procedures at α < 0. 01. �However, at increased values of α, this procedure is considered to be more powerful and more precise. �Calculations are the same for t and ψD. �Table is different.

DUNN-SIDAK PROCEDURE �However, it is not easy to allocate the total value of α unevenly across a particular set of comparisons. �This is because the values of α for each individual comparison are related multiplicatively, as opposed to additively. �Thus, you can’t simply add the α’s for each comparison together to get the total value of α for all contrasts combined.

DUNNETT’S TEST �For contrasts involving a control mean. �Also uses a t statistic (t. D’) and critical difference (ψD’). �Calculations are the same for t and ψ. �Different table. �Instead of C, you use k, the number of means (including the control mean). �Note: unlike Dunn’s and Dunn-Sidak’s, Dunnet’s procedure is limited to k-1 non-orthogonal comparisons.

CHOOSING A PROCEDURE : A PRIORI NON-ORTHOGONAL TESTS �Often, the use of more than one procedure will appear to be appropriate. �In such cases, compute the critical difference (ψ) necessary to reject the null hypothesis for all of the possible procedures. �Use the one that gives the smallest critical difference (ψ) value.

A PRIORI ORTHOGONAL and NONORTHOGONAL CONTRASTS �The advantage of being able to make all planned contrasts, not just those that are orthogonal, is gained at the expense of an increase in the probability of making Type 2 errors.

A PRIORI and A POSTERIORI NONORTHOGONAL CONTRASTS �When you have a large number of means, but only comparatively very few contrasts, a priori non-orthogonal contrasts are better suited. �However, if you have relatively few means and a larger number of contrasts, you may want to consider doing an a posteriori test instead.

A POSTERIORI CONTRASTS �There are many kinds, all offering different degrees of protection from Type 1 and Type 2 errors: Least Significant Difference (LSD) Test Tukey’s Honestly Significant Difference (HSD) Test Spjtotvoll and Stoline HSD Test Tukey-Kramer HSD Test Scheffé’s S Test Brown-Forsythe BF Procedure Newman-Keuls Test Duncan’s New Multiple Range Test

A POSTERIORI CONTRASTS �Most are good for doing all possible pair- wise comparisons between means. �One (Scheffé’s method) allows you to evaluate all possible contrasts between means, whether they are pair-wise or not.

CHOOSING AN APPROPRIATE TEST PROCEDURE �Trade-off between power and the probability of making Type 1 errors. �When a test is conservative, it is less likely that you will make a Type 1 error. �But it also would lack power, inflating the Type 2 error rate. �You will want to control the Type 1 error rate without loosing too much power. �Otherwise, you might reject differences between means that are actually significant.

DOING PLANNED CONTRASTS USING SAS �You have a data set with one dependent variable (y) and one independent variable (a). �(a) has 4 different treatment levels (1, 2, 3, and 4). �You want to do the following comparisons between treatment levels: 1)Y 1 -Y 2 2) Y 3 -Y 4 3) (Y 1 -Y 2)/2 - (Y 3 -Y 4)/2

ARE THEY ORTHOGONAL? SET 1 cijci’j ∑cijci’j COEFFICIENTS CONTRASTS c 1 c 2 c 3 c 4 1 -1 - - Y 1 -Y 2 - - 1 -1 Y 3 -Y 4 ½ ½ -1/2 1/2 -1/2 ½ (Y 2+Y 2)/2 – (Y 3+Y 4)/2 0 YES!. . . BUT THEY DON’T HAVE TO BE

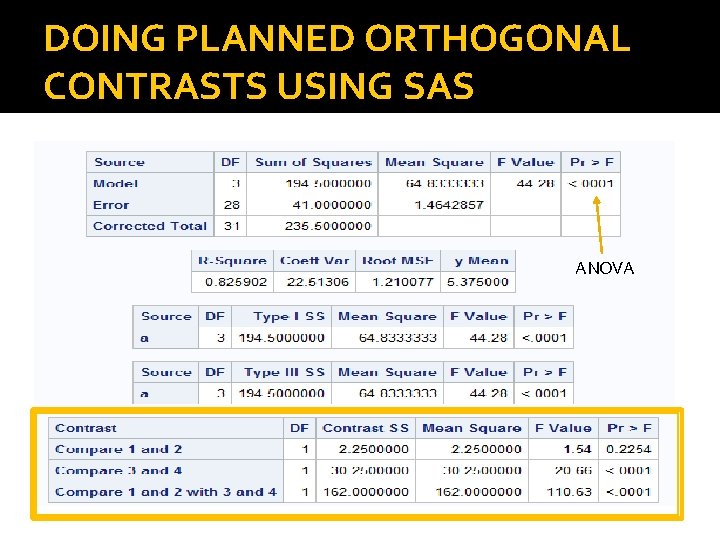
DOING PLANNED ORTHOGONAL CONTRASTS USING SAS � SAS INPUT: dataset; Give your dataset an informative name. input y a; Tell SAS what you’ve inputted: column 1 is cards; your y variable (dependent) and column 2 is 3 1 your a variable (independent). 4 2 7 3 This is followed by your actual data. 7 4. . . “Model” tells SAS that Use SAS procedure proc glm; class a; “Class” tells SAS that a is categorical. you want to look at the effects that a has on y. model y = a; contrast 'Compare 1 and 2' a 1 -1 0 0; Indicate “weights” (kind of contrast 'Compare 3 and 4' a 0 0 1 -1; contrast 'Compare 1 and 2 with 3 and 4' a 1 1 -1 -1; like the coefficients). run; Then enter your “contrast” statements.

DOING PLANNED ORTHOGONAL CONTRASTS USING SAS ANOVA

RECOMMENDED READING �Kirk RE. 1982. Experimental design: procedures for the behavioural sciences. Second ed. CA: Wadsworth, Inc. �Field A, Miles J. 2010. Discovering Statistics Using SAS. London: SAGE Publications Ltd. �Institute for Digital Research and Education at UCLA: http: //www. ats. ucla. edu/stat/ Stata, SAS, SPSS and R.

A PRIORI OR PLANNED CONTRASTS THE END

EXTRA SLIDES

PLANNED COMPARISONS USING A t STATISTIC �t = ∑cj. Yj/ √MSerror∑cj/nj Where c is the coefficient, Y is the corresponding mean, n is the sample size, and MSerror is the Mean Square Error.

PLANNED COMPARISONS USING A t STATISTIC �For Example, you want to compare 2 means: Y 1 = 48. 7 and Y 2=43. 4 c 1 = 1 and c 2 = -1 n=10 MSerror=28. 8 �t = (1)48. 7 + (-1)43. 4 [√ 28. 8(12/10) + (-12/10)] = 2. 21

CONFIDENCE INTERVALS FOR ORTHOGONAL CONTRASTS �(Y 1 -Y 2) – tα/2, v(SE) ≤ ψ ≤ (Y 1 -Y 2) – tα/2, v(SE) �For Example: If, Y 1 = 48. 7, Y 2 = 43. 4, and SE(tα(2), df) = 4. 8 (Y 1 -Y 2) – SE(tα(2), df) = 0. 5 (Y 1 -Y 2) + SE(tα(2), df) = 10. 1 Thus, you can be 95% confident that the true value of ψ is between 0. 5 and 10. 1. Because the confidence interval does not include 0, you can also reject the null hypothesis that Y 1 -Y 2 = 0. (Example after Kirk 1982)

TYPE I ERRORS AND ORTHOGONAL CONTRASTS �As the number of independent tests increases, so does the probability of committing a Type 1 error. �For Example, when α = 0. 05: 1 -(1 -0. 05)3=0. 14 (C=3) 1 -(1 -0. 05)5=0. 23 (C=5) 1 -(1 -0. 05)10=0. 40 (C=10) (Example after Kirk 1982)