Chapter 12 A Priori and Post Hoc Comparisons

Linear Contrasts • You think that Freshman and Seniors will have different levels of

Linear Contrasts • Allows for the comparison of one group or set of groups

Linear Contrasts a = weight given to a group

Linear Contrasts 1 2 3 a 1 = 0, a 2 = 0, a

SS Contrast • You can use the linear contrast to compute a SS contrast

SS Contrasts a 1 =. 5, a 2 = -. 5, a 3 =

SS Contrasts a 1 = 1, a 2 = -1, a 3 = -1,

F Test Fresh & Senior vs. Sophomore & Junior

F Test Fresh & Senior vs. Sophomore & Junior F crit (1, 20) =

Make contrasts to determine 1) If seniors are happier than everyone else? 2) If

1) If seniors are happier than everyone else? a 1 = -1, a 2

2) If juniors and sophomores have different levels of happiness? a 1 = 0,

Practice • To investigate the maternal behavior of lab rats, we move the rat

Contrasts • Some contrasts are independent – Freshman vs. Sophomore (1, -1, 0, 0)

Orthogonal Contrasts • If you have a complete set of orthogonal contrasts • The

Orthogonal Contrasts • 1) ∑ aj = 0 – Already talked about • 2)

Orthogonal Contrasts • ∑ a j bj = 0 • Fresh, Sophomore, Junior, Senior

Orthogonal Contrasts • Lets go to five groups • What would the complete set

Orthogonal Contrasts • General rule • There is more than one right answer

Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs.

Orthogonal Contrasts • 1) ∑ aj = 0 • 2) ∑ aj bj =

Orthogonal Contrasts • • A) 3, 3, -2, -2 B) 1, -1, 0, 0,

Compute a complete set of orthogonal contrasts for the following data. Test each of

Orthogonal Contrasts Fresh, Soph, Jun, Sen Fresh & Soph Fresh vs. Soph 1, 1,

1, 1, -1 L=1 SScontrast = 1. 5; F =. 014 1, -1, 0,

SScontrast = 1. 5 SScontrast = 48 SScontrast = 1587 1. 5 + 48

Orthogonal Contrasts • Why use them? • People like that they sum together •

Slides: 58

Download presentation

Chapter 12 • A Priori and Post Hoc Comparisons • • Multiple t-tests Linear Contrasts Orthogonal Contrasts Trend Analysis Bonferroni t Fisher Least Significance Difference Studentized Range Statistic Dunnett’s Test

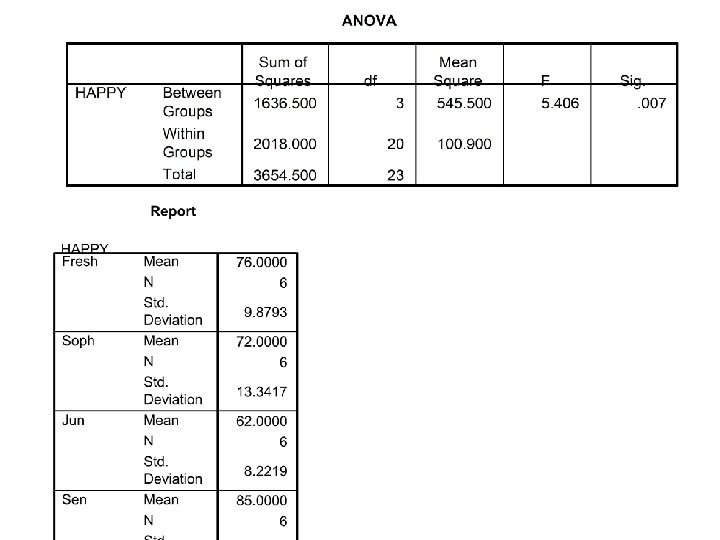
Linear Contrasts • You think that Freshman and Seniors will have different levels of happiness than Sophomores and Juniors

Linear Contrasts • Allows for the comparison of one group or set of groups with another group or set of groups

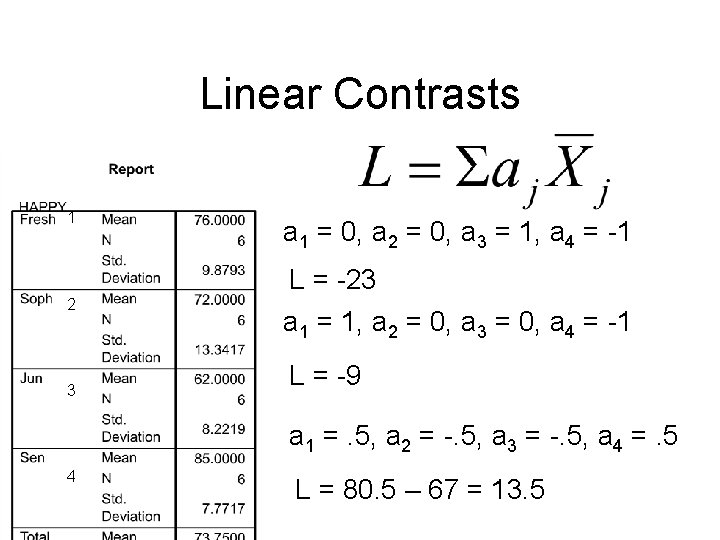
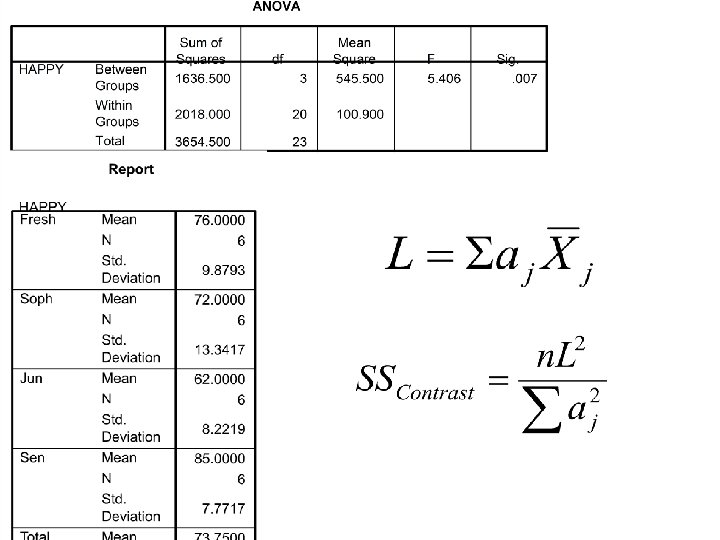
Linear Contrasts a = weight given to a group

Linear Contrasts 1 2 3 a 1 = 0, a 2 = 0, a 3 = 1, a 4 = -1 L = -23 a 1 = 1, a 2 = 0, a 3 = 0, a 4 = -1 L = -9 a 1 =. 5, a 2 = -. 5, a 3 = -. 5, a 4 =. 5 4 L = 80. 5 – 67 = 13. 5

SS Contrast • You can use the linear contrast to compute a SS contrast • SS contrast is like SS between • SS contrast has 1 df • SS contrast is like MS between

SS Contrast

SS Contrasts a 1 =. 5, a 2 = -. 5, a 3 = -. 5, a 4 =. 5 L = 80. 5 – 67 = 13. 5

SS Contrasts a 1 =. 5, a 2 = -. 5, a 3 = -. 5, a 4 =. 5 L = 80. 5 – 67 = 13. 5 n=6 L = 13. 5 Sum a 2 =. 52+-. 52+ -. 52 +. 52 = 1

SS Contrasts a 1 = 1, a 2 = -1, a 3 = -1, a 4 = 1 L = 161 – 134 = 27

SS Contrasts a 1 = 1, a 2 = -1, a 3 = -1, a 4 = 1 L = 161 – 134 = 27 n=6 L = 27 Sum a 2 = 12+-12+ -12 + 12 = 4

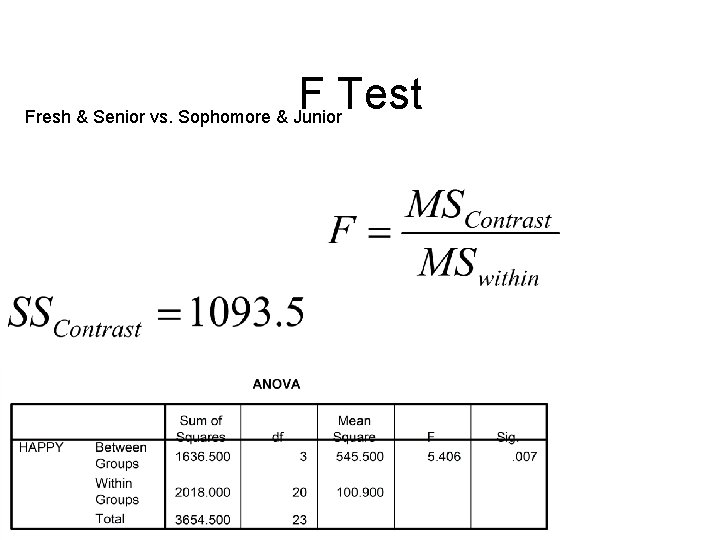
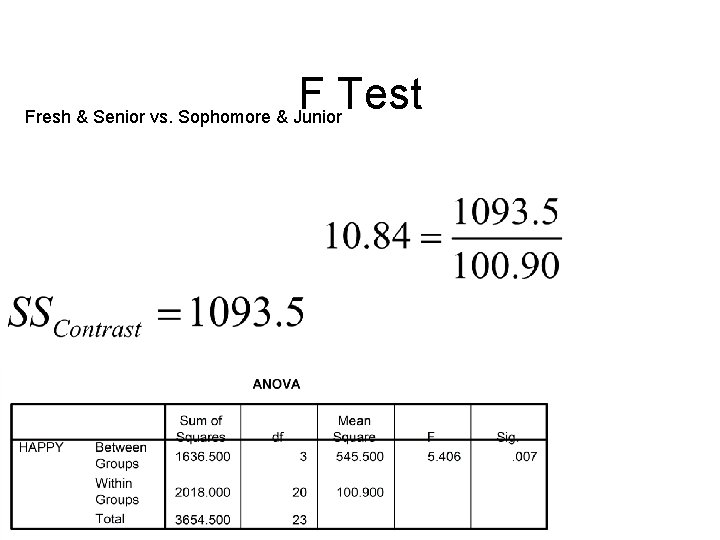
F Test Note: MS contrast = SS contrast

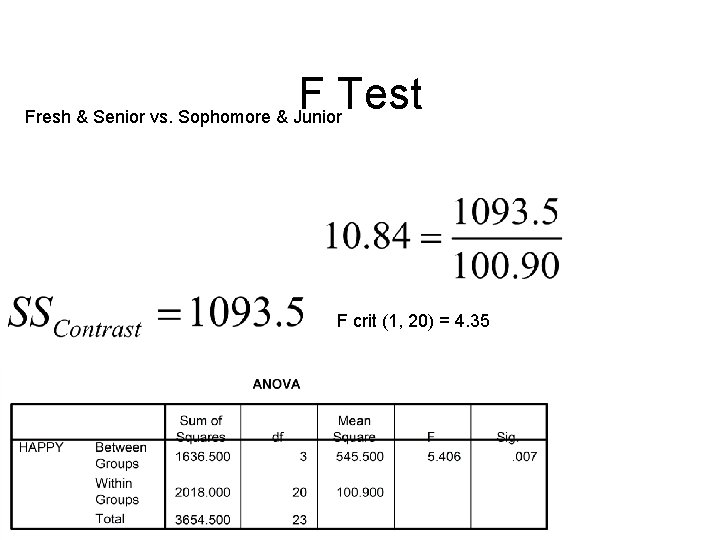
F Test Fresh & Senior vs. Sophomore & Junior

F Test Fresh & Senior vs. Sophomore & Junior F crit (1, 20) = 4. 35

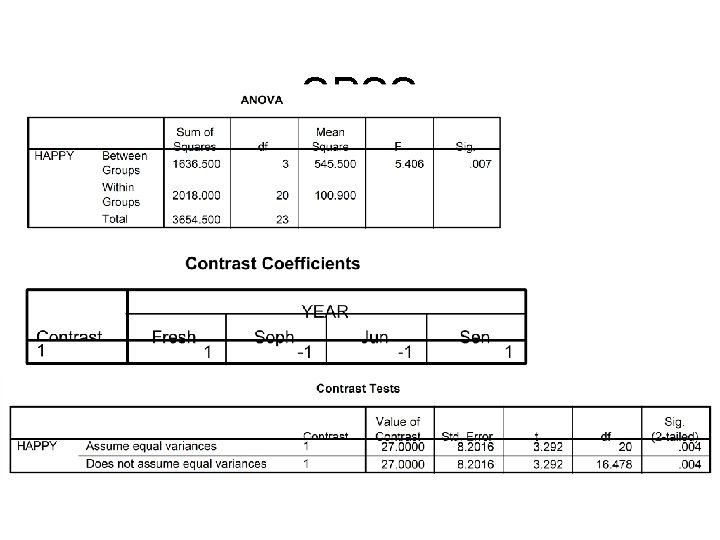
SPSS

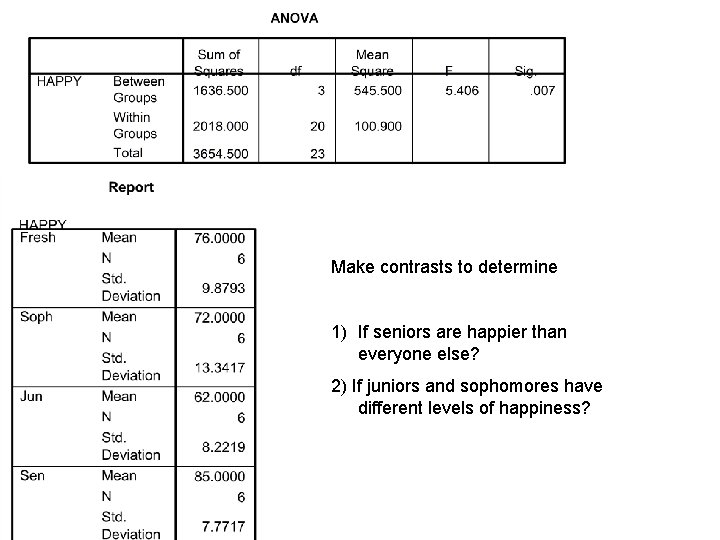
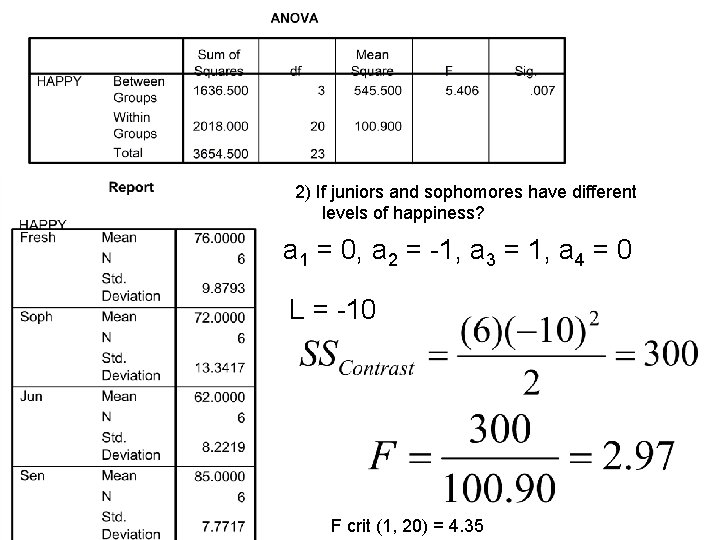
Make contrasts to determine 1) If seniors are happier than everyone else? 2) If juniors and sophomores have different levels of happiness?

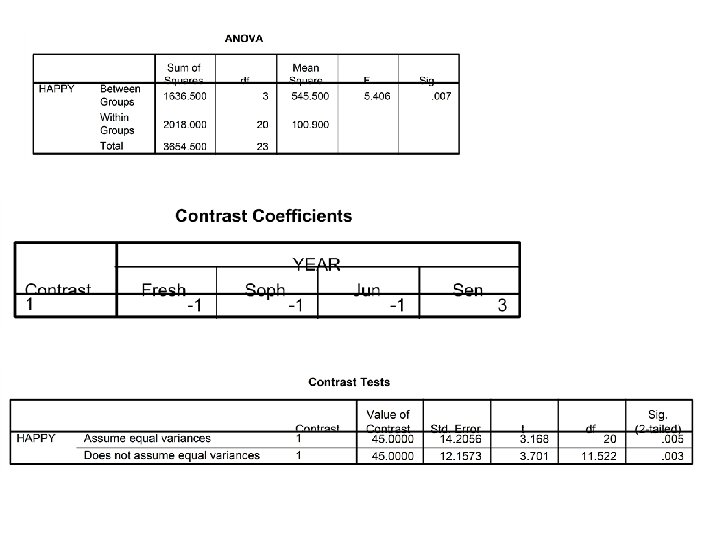
1) If seniors are happier than everyone else? a 1 = -1, a 2 = -1, a 3 = -1, a 4 = 3 L = 45 F crit (1, 20) = 4. 35

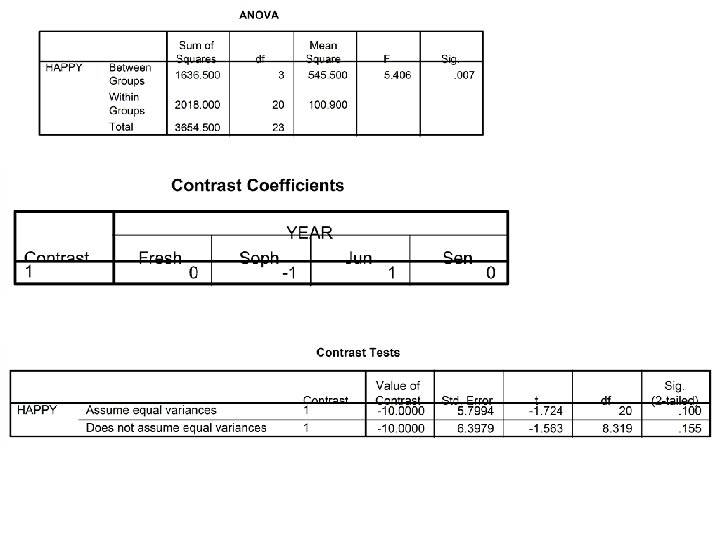
2) If juniors and sophomores have different levels of happiness? a 1 = 0, a 2 = -1, a 3 = 1, a 4 = 0 L = -10 F crit (1, 20) = 4. 35

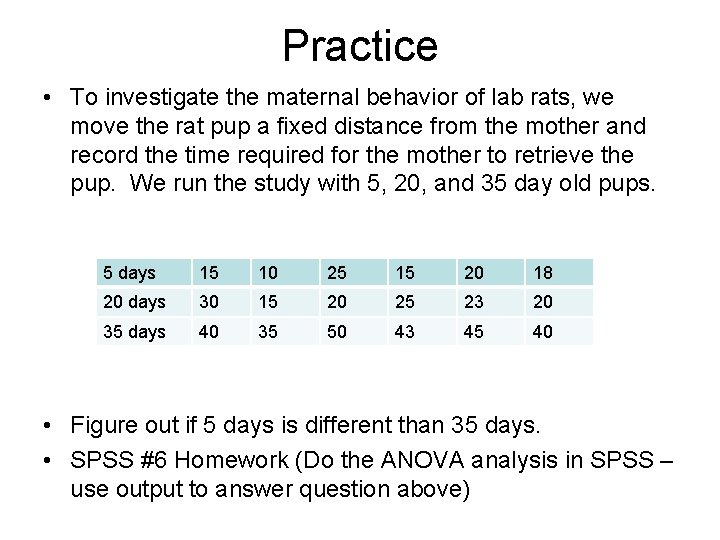
Practice • To investigate the maternal behavior of lab rats, we move the rat pup a fixed distance from the mother and record the time required for the mother to retrieve the pup. We run the study with 5, 20, and 35 day old pups. 5 days 15 10 25 15 20 18 20 days 30 15 20 25 23 20 35 days 40 35 50 43 45 40 • Figure out if 5 days is different than 35 days. • SPSS #6 Homework (Do the ANOVA analysis in SPSS – use output to answer question above)

Contrasts • Some contrasts are independent – Freshman vs. Sophomore (1, -1, 0, 0) – Junior vs. Senior (0, 0, 1, -1) • Some are not – Freshman vs. Sophomore, Junior, Senior (3, -1, -1) – Freshman vs. Sophomore & Junior (2, -1, 0)

Orthogonal Contrasts • If you have a complete set of orthogonal contrasts • The sum of SScontrast = SSbetween

Orthogonal Contrasts • 1) ∑ aj = 0 – Already talked about • 2) ∑ aj bj = 0 – Ensures contrasts of independent of one another • 3) Number of comparisons = K -1 – Ensures enough comparisons are used

Orthogonal Contrasts • ∑ a j bj = 0 • Fresh, Sophomore, Junior, Senior • (3, -1, -1) and (2, -1, 0) • (3*2)+(-1*-1) = 8

Orthogonal Contrasts • ∑ a j bj = 0 • Fresh, Sophomore, Junior, Senior • (-1, 1, 0, 0) & (0, 0, -1, 1) • (-1*0)+(-1*0)+(1*0) = 0 • *Note: this is not a complete set of contrasts (rule 3)

Orthogonal Contrasts • Lets go to five groups • What would the complete set contrasts be that would satisfy the earlier rules?

Orthogonal Contrasts • General rule • There is more than one right answer

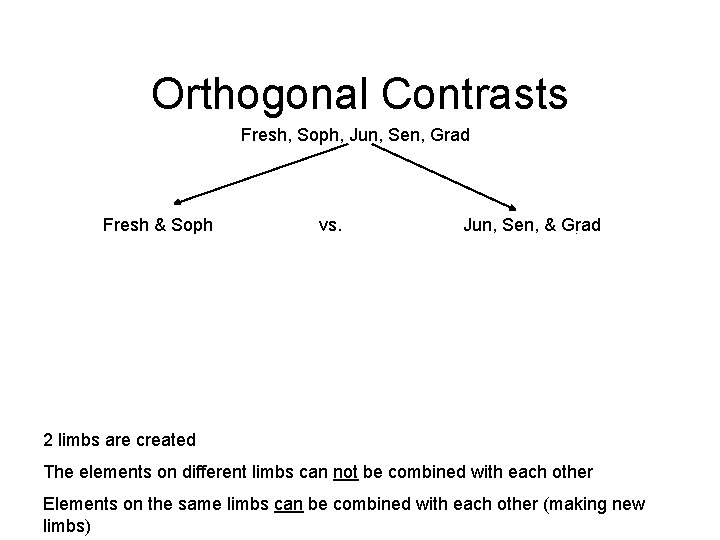
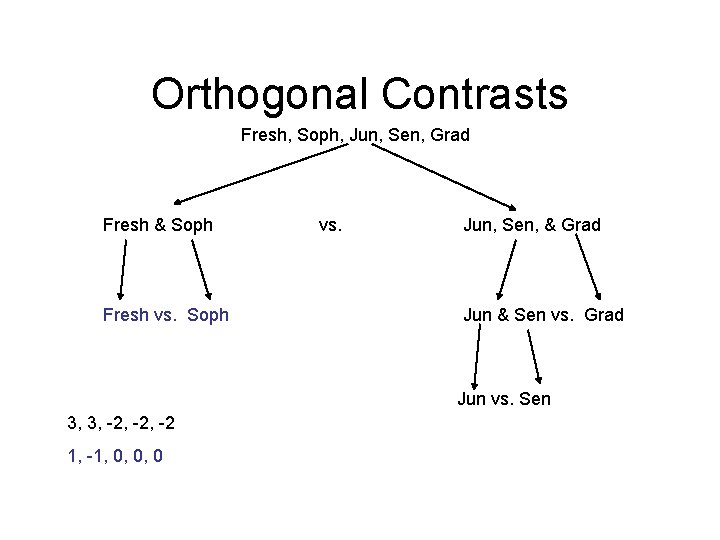
Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen

Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen 2 limbs are created The elements on different limbs can not be combined with each other Elements on the same limbs can be combined with each other (making new limbs)

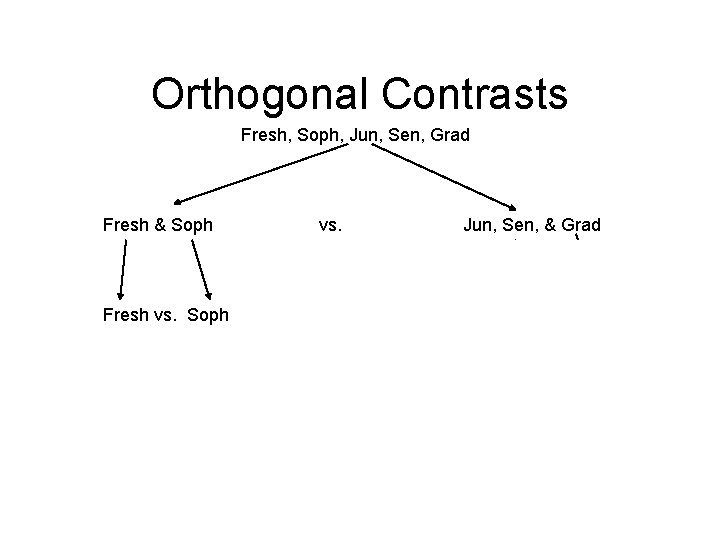
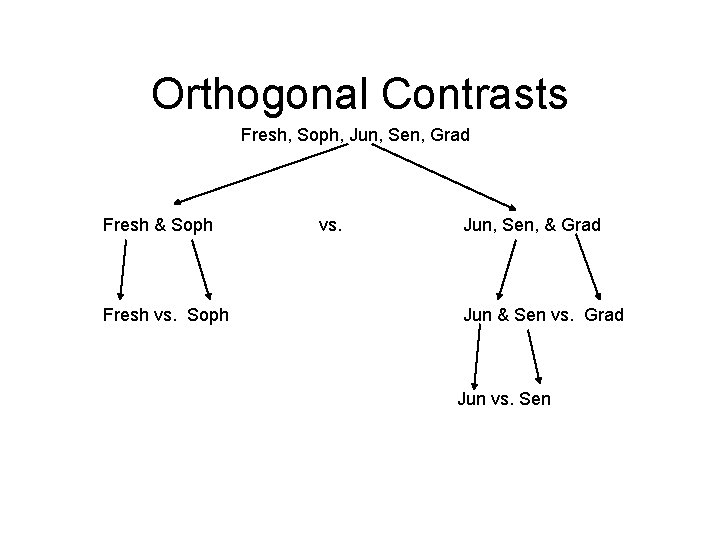
Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen

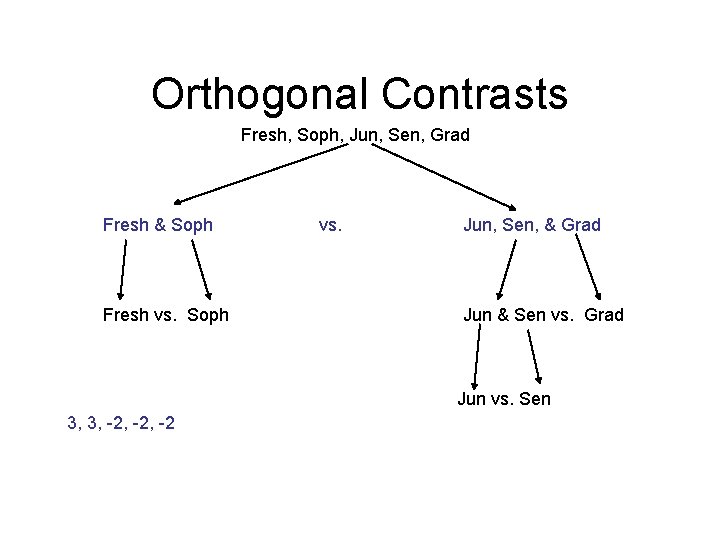
Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen 3, 3, -2, -2

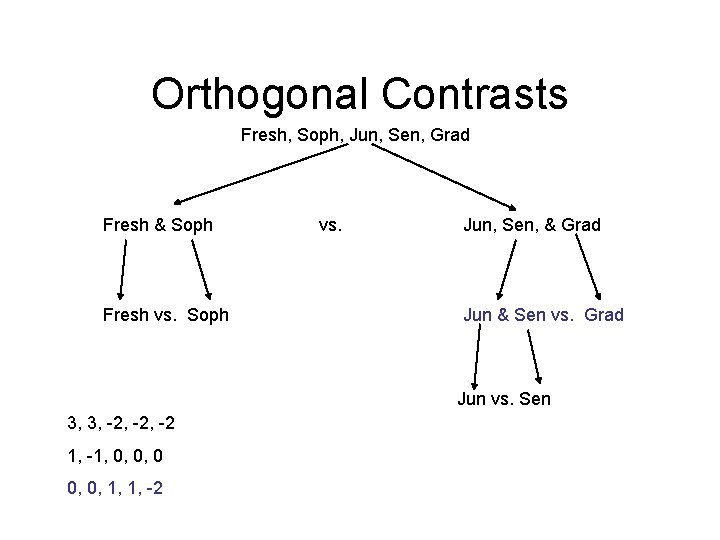
Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen 3, 3, -2, -2 1, -1, 0, 0, 0

Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen 3, 3, -2, -2 1, -1, 0, 0, 0, 1, 1, -2

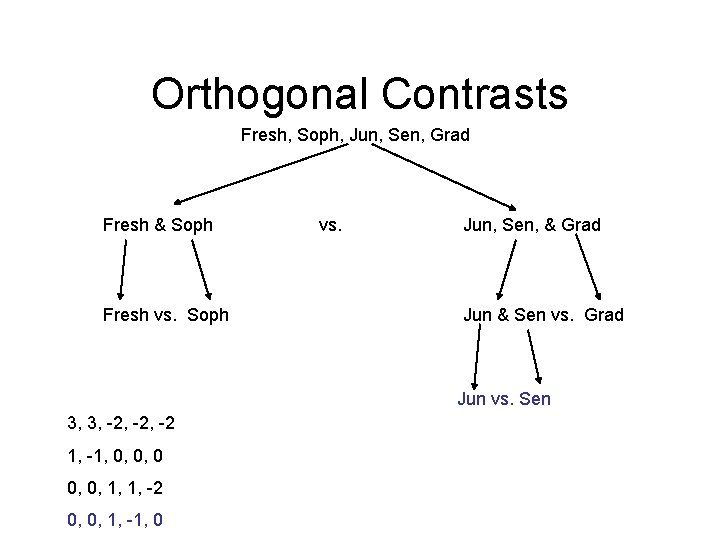
Orthogonal Contrasts Fresh, Soph, Jun, Sen, Grad Fresh & Soph Fresh vs. Soph vs. Jun, Sen, & Grad Jun & Sen vs. Grad Jun vs. Sen 3, 3, -2, -2 1, -1, 0, 0, 0, 1, 1, -2 0, 0, 1, -1, 0

Orthogonal Contrasts • 1) ∑ aj = 0 • 2) ∑ aj bj = 0 • 3) Number of comparisons = K -1 • • 3, 3, -2, -2 1, -1, 0, 0, 0, 1, 1, -2 0, 0, 1, -1, 0

Orthogonal Contrasts • 1) ∑ aj = 0 • 2) ∑ aj bj = 0 • 3) Number of comparisons = K -1 • • 3, 3, -2, -2 1, -1, 0, 0, 0, 1, 1, -2 0, 0, 1, -1, 0 = = 0 0

Orthogonal Contrasts • • A) 3, 3, -2, -2 B) 1, -1, 0, 0, 0 C) 0, 0, 1, 1, -2 D) 0, 0, 1, -1, 0 • A, B = 0; A, C = 0; A, D = 0 • B, C = 0; B, D = 0 • C, D = 0

Orthogonal Contrasts • If you have a complete set of orthogonal contrasts • The sum of SScontrast = SSbetween

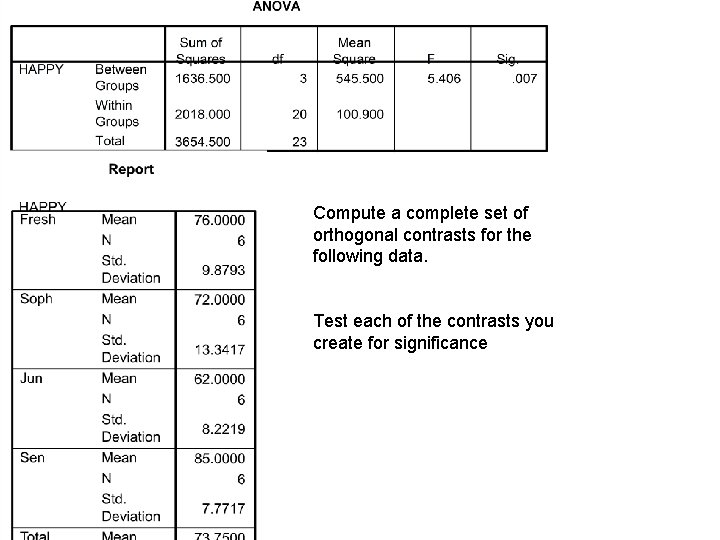
Compute a complete set of orthogonal contrasts for the following data. Test each of the contrasts you create for significance

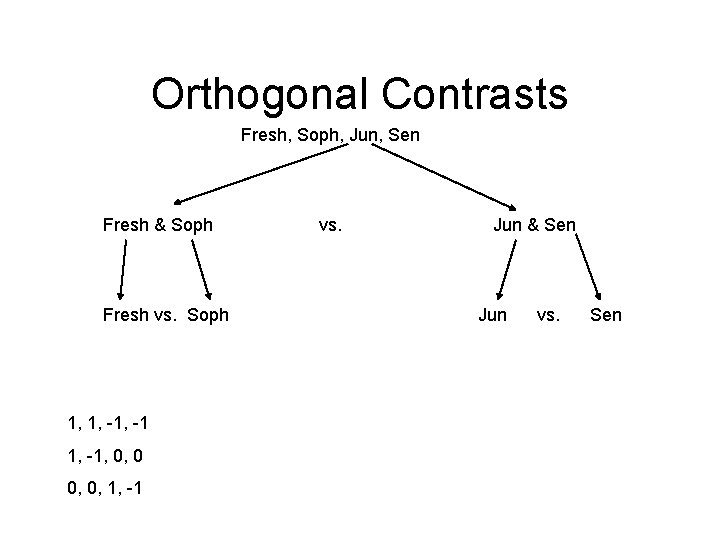
Orthogonal Contrasts Fresh, Soph, Jun, Sen Fresh & Soph Fresh vs. Soph 1, 1, -1, 0, 0, 1, -1 vs. Jun & Sen Jun vs. Sen

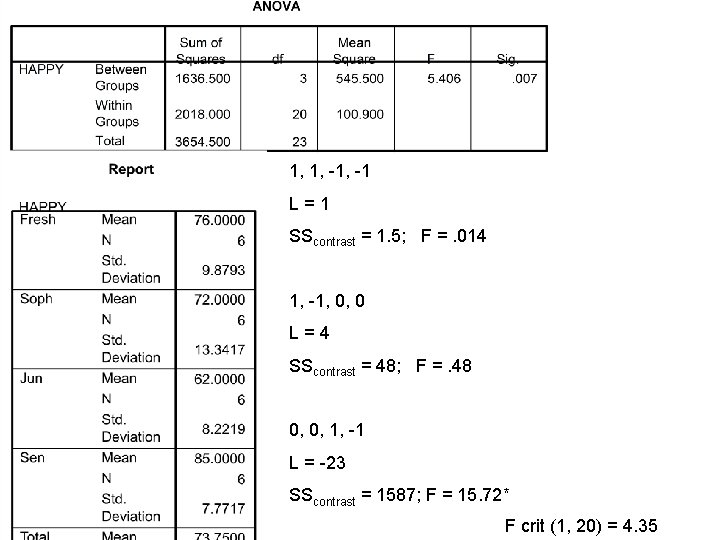
1, 1, -1 L=1 SScontrast = 1. 5; F =. 014 1, -1, 0, 0 L=4 SScontrast = 48; F =. 48 0, 0, 1, -1 L = -23 SScontrast = 1587; F = 15. 72* F crit (1, 20) = 4. 35

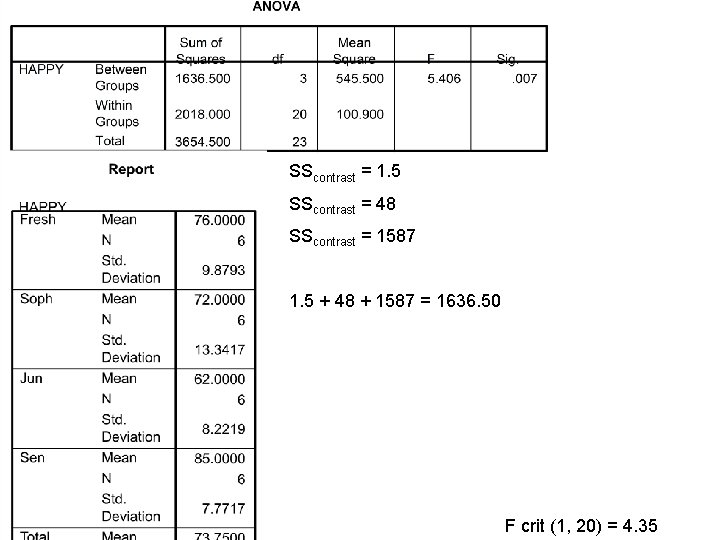
SScontrast = 1. 5 SScontrast = 48 SScontrast = 1587 1. 5 + 48 + 1587 = 1636. 50 F crit (1, 20) = 4. 35

Orthogonal Contrasts • Why use them? • People like that they sum together • People like that they are independent • History • I would rather have contrasts based on reason then simply because they are orthogonal!