Sonia Taras Sonia Spanu Andrea Pittorra q q

Sonia Taras Sonia Spanu Andrea Pittorra

q q q q q Cosa sono le equazioni Classificazione delle equazioni. Struttura delle equazioni di I grado. La soluzione. Classificazione in base al numero delle soluzioni. Equazione ridotta a forma normale. Primo principio di equivalenza. Secondo principio di equivalenza Risoluzione di una ‘equazione di primo grado Verifica soluzioni di un’equazione.

2 x+5 x-2=-4 x+3 -7 x Trasportiamo al primo membro tutti i termini che contengono l’incognita cambiandoli di segno 2 x+5 x +7 x + 4 x -2=-+3 Trasportiamo al secondo membro tutti i termini noti cambiandoli di segno 2 x+5 x +7 x + 4 x =+3 +2

A cura di: Frau Francesco Pala Francesca Patta Simona Francesca

Che cosa sono? Formula risolutiva I 3 tipi di equazioni Trinomio di secondo grado Regola di Cartesio

L’ equazione di secondo grado è un trinomio eguagliato a zero. Ax 2+bx+c=0 Esempio: 4 x 2+4 x+1=25 Si può notare che il primo membro dell’equazione è il quadrato di un binomio Quindi si può scrivere anche: (2 x+1)2= 25 2 x+1= +/-5 2 x=+5 -1 2 x= -5 -1 X=2 X= -3

Formula risolutiva La formula risolutiva è il metodo che utilizziamo in una equazione di 2° grado per trovare x 1 e x 2. Una volta trovati i valori suddetti, l’equazione è stata completata. X 1, 2: -b+/-√b 2 -4(a)(c) 2(a)

Pura Spuria I 3 tipi di equazione Completa

Si dice equazione quadratica spuria un'equazione quadratica che manca del termine noto, ossia avente la forma: ax 2+bx=0 Un'equazione di questo tipo si risolve facilmente tramite scomposizione: X= (ax+b)=0 Per la legge di annullamento del prodotto quest’equazione è equivalente alle due: X= 0 ax+b=0 E in definitiva le sue soluzioni sono: X=- b a

Si dice equazione quadratica pura un'equazione polinomiale di secondo grado che manca del termine di primo grado, cioè che è della forma: ax 2+c = 0 Portando c al secondo membro e dividendo per a si ottiene: x 2=-c/a l'equazione non ammette soluzioni reali (ma due soluzioni immaginarie); viceversa, se: -c/a > 0 l'equazione è risolta da: X = +-√-c/a

Consideriamo il polinomio completo di secondo grado: ax 2+bx+c e supponiamo anche il discriminante dell'equazione che si ottiene uguagliando a zero il polinomio sia positivo. Motiplicando e dividendo per a si ottiene: a (x 2 + b x + c ) a a Dunque: Abbiamo già trovato prima che X 1 + x 2 = - b a e X 1*x 2=c a A [x 2 +- (x 1+x 2) x + x 1 x 2] = a [ x 2 – x 1 x – x 2 x + x 1 x 2] = a [ x (x – x 1) – x 2 (x – x 1)] = a (x – x 1) (x – x 2)

Regola di Cartesio Si considerino i coefficienti a, b, c di un'equazione di secondo grado avente radici reali, si dice che si ha una permanenza se due coefficienti consecutivi sono concordi, si ha una variazione se sono discordi. La regola di Cartesio permette di ricavare i segni delle soluzioni di un'equazione di secondo grado essa afferma: In un'equazione di secondo grado avente radici reali il numero di di soluzioni negative è uguale al numero di permanenze, mentre il numero di soluzioni positive è uguale al numero di variazioni. Esempio: x 2 -5 x+6=0, siccome a=1 b=-5 c=6 ci sono due variazioni si hanno due soluzioni positive infatti esse sono x 1=2 e x 2=3. Attenzione a regola di Cartesio si applica solo se il discriminante non è negativo, infatti in tal caso le radici sono immaginarie.

A cura di: Canu Andrea Costaggiu Claudio Dessì Chiara

I punti che toccheremo Definizione di equazione di 3° e 4° grado Come risolvere un equazione di 3° e 4° grado Esempio di equazione di 3° e 4° grado

Esistono due tipi di equazione di 3° grado: Equazioni reciproche di 3° grado di prima specie. u Equazioni reciproche di 3° grado di seconda specie. u

Definizione di un equazione di 3° grado di prima specie • Un equazione di terzo grado reciproca di prima specie è un polinomio di terzo grado ordinato e completo, in cui i coefficienti dei termini estremi e di quelli equidistanti dagli estremi sono uguali, uguagliato a zero. ax 3+bx 2+bx+a=0

Risoluzione di un equazione di 3° grado di prima specie. u u u u ax 3+bx 2+bx+a=0 a(x 3+1)+bx(x+1)=0 a(x+1)(x 2 -x+1)+bx(x+1)=0 (x+1)[a(x 2 -x+1)+bx]=0 (x+1)[ax 2 -ax+a+bx]=0 Legge di 2 (x+1)[ax +(b-a)x+a]=0 annullamento del prodotto {x+1=0 {ax 2+(b-a)x+a=0 u x 1=-1 x 2=-(b-a)+ (b-a)2 -4 a 2 u x 3=-(b-a)- 2 a(b-a)2 -4 a 2 u 2 a Risolvendo le rispettive operazioni otterremo i risultati delle X.

Esempio numerico di equazione di 3° grado di prima specie u u u u u 6 x 3+5 x 2+5 x+6=0 6(x 3+1)5 x(x+1)=0 6 x 2 -x+6=0 6(x+1)(x 2 -x+1)+5 x(x+1)=0 (x+1)[6(x 2 -x+1)+5 x]=0 a= 6 (x+1)[6 x 2 -6 x+6+5 x]=0 b= 1 2 (x+1)[6 x -x+6]=0 c= 6 X+1=0 6 x 2 -x+6=0 x 1=-1 X 2, 3=-b + - b 2 -4 ac 2 a Risolvendo la rispettiva operazione otterremo i risultati delle X.

Definizione di un equazione di 3° grado di seconda specie Un equazione di terzo grado reciproca di seconda specie è un polinomio di terzo grado ordinato e completo, in cui i coefficienti dei termini estremi e di quelli equidistanti dagli estremi sono opposti, uguagliato 3 a zero. ax +bx 2 -bx-a=0

Risoluzione di un equazione di 3° grado di seconda specie u ax 3+bx 2 -bx-a=0 a(x 3 -1)+bx(x-1)=0 a(x-1)(x 2+x+1)+bx(x-1)=0 (x-1)[a(x 2+x+1)+bx]=0 (x-1)[ax 2+ax+a+bx]=0 x-1=0 ax 2+(b+a)x+a=0 u x 1= +1 u x 2= -(b+a)+ (b+a)2 -4 a 2 u u u 2 a u x 3= -(b+a)-4 a 2 2 a Legge di annullamento del prodotto Risolvendo le rispettive operazioni otterremo i risultati delle X

Esempio numerico di equazione di 3° grado di seconda specie u u u u u 12 x 3 -37 x 2+37 x-12=0 12(x 3 -1)37 x(x-1)=0 12(x-1)(x 2+x+1)-37 x(x-1)=0 (x-1)[12(x 2+x+1)-37 x]=0 (x-1)[12 x 2+12 x+12 -37 x]=0 (x-1)[12 x 2 -25 x+12]=0 x-1=0 12 x 2 -25 x+12=0 x 1=1 x 2= 4 3 u x 3= 3 4

Esistono due tipi di equazioni di 4° grado: Equazioni reciproche di 4° grado di prima specie. u Equazioni reciproche di 4° grado di seconda specie. u

Definizione di un equazione di 4° grado di prima specie u L’equazione di quarto grado di prima specie, è un polinomio di quarto grado ordinato e completo, in cui i coefficienti dei termini estremi e di quelli equidistanti dagli estremi sono uguali, uguagliato a zero. ax 4+bx 3+cx 2+bx+a=0

Risoluzione di un equazione di 4° grado di prima specie… u ax 4+bx 3+cx 2+bx+a=0 x 2 u x 2 x 2 ax 2+bx+c+b+a=0 1 x x 2 u a(x 2+ x 2 1 )+b(x+ x 1 u a[(x+x 1 x )2 -2]+b(x+ u u u a[y 2 -2]+by+c=0 ay 2 -2 a+by+c=0 ay 2+by-2 a+c=0 )+c=0 y 1 ottengo = y 2

…continuo equazione di 4° grado di prima specie(2)… u Le y le abbiamo ottenute con la seguente formula risolutiva: + u Y 1, 2= -b 2 a b 2 -4 ac = Ora bisogna sostituire a : x + x+ 1 x y 1 = 1 x i valori delle y. Otteniamo con il m. c. m. y 2 Otteniamo con il m. c. m. X 2 -Y 1 X+1=0 X 2 -Y 2 X+1=0

…continuo equazione di 4° grado di seconda specie(3). u u u Ora risolvendo le due equazioni di secondo grado otteniamo i risultati delle x. x 1 x 2 -y 1 x+1=0 x 2 -y 2 x+1=0 x 2 x 3 x 4

Esempio numerico di equazione di 4° grado di prima specie… u 6 x 4 -5 x 3 -38 x 2 -5 x+6=0 u 4 -5 x 3 -38 x 2 -5 x+6=0 6 x 2 x 2 x 2 u x x 2 6 x 2 -5 x-38 -5+6=0 1 x 2 u u 6(x 2+ 1 x )-5(x+ 1 1 x x 6[(x+ )2 -2]-5(x+ 6(y 2 -2)-5 y-38=0 6 y 2 -12 -5 y-38=0 2 Divido tutti i termini per x 2 )-38=0

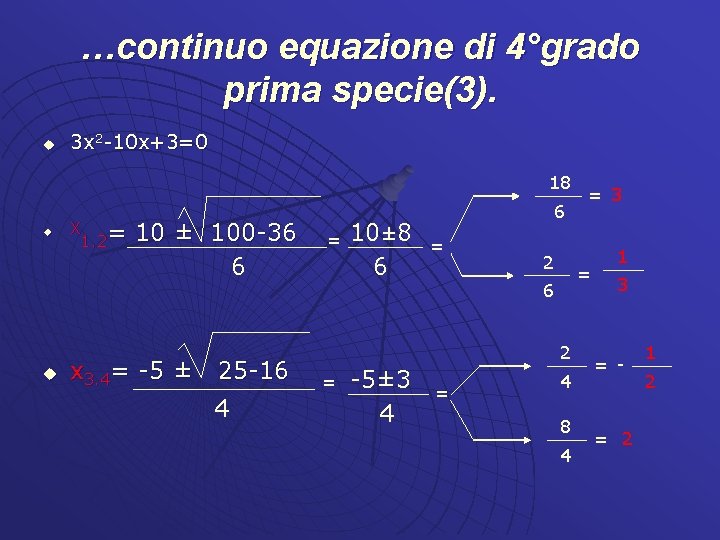
…continuo equazione di 4° grado di prima specie(2)… u Y 1. 2= 5 ± 25 -1200 12 5+35 u 12 5± 35 12 535 12 40 10 12 3 36 5 12 2 m. c. m x+ 1 10 = x 3 ; x+ 1 5 = x 2 m. c. m 2 x 2+2=-5 x= 2 x 2+5 x+2=0 3 x 2+3=10 = 3 x 2 -10 x+3=0

…continuo equazione di 4°grado prima specie(3). u 3 x 2 -10 x+3=0 18 u u X 1. 2= 10 ± 100 -36 6 x 3. 4= -5 ± 25 -16 4 = 10± 8 6 6 = 2 = 6 2 = -5± 3 4 = = 3 4 8 4 1 3 = - = 2 1 2

Definizione di un equazione di 4° grado di seconda specie u L’equazione di quarto grado di prima specie, è un polinomio di quarto grado ordinato e completo, in cui i coefficienti dei termini estremi e di quelli equidistanti dagli estremi sono opposti, uguagliato a zero. ax 4+bx 3 -bx-a=0

Risoluzione di un equazione di 4° grado di seconda specie u u u ax 4+bx 3 -bx-a=0 a(x 4+1)+bx(x 2 -1)=0 a(x 2 -1)(x 2+1)+bx(x 2 -1)=0 (x 2 -1)[a(x 2 -1)+bx]=0 (x 2 -1)[ax 2 -a+bx]=0 (x 2 -1)[ax 2+bx-a]=0 x 2 -1=0 ax 2+bx-a=0 x 1= x 2= x 3= x 4=

Esempio numerico di equazione di 4° grado di seconda specie u u u u 2 x 4+5 x 3 -5 x-2=0 2(x 4 -1)5 x((x 2 -1)=0 2(x 2 -1)(x 2+1)+5 x(x 2 -1)=0 (x 2 -1)[(2(x 2+1)+5 x]=0 (x 2 -1)[2 x 2+2+5 x]=0 (x 2 -1)[2 x 2+5 x+2]=0 Legge di 2 x -1=0 annullamento del prodotto 2 2 x +5 x+2=0

…continuo equazione di 4° grado di seconda specie(2). u Ora risolviamo l’equazione: 2 x 2+5 x+2=0 -5+3 u x 3. 4 =-5+- 25 -4*2(2) 4 = -5+-3 4 4 -5 -3 4 = = 2 1 2

EQUAZIONI PARAMETRICHE Roberta Floris u Elisabetta Melinu u Cristina Carta u

Un’ equazione di secondo grado si dice parametrica se almeno uno dei coefficienti dipende da una o più variabili dette parametri.

Ecco un’esempio di equazione parametrica: x² +Kx+2 k=0 Dove b è uguale a k e c é uguale a 2 k.

Data l’equazione parametrica: x² +Kx+2 k=0 trovare i valori di k in modo che le radici siano reali. La condizione da verificare è:

Nel nostro caso, a=1, b=k, c=2 k, per cui: k²-4(1)(2 k)≥ 0 K²-8 k≥ 0 K(k-8)≥ 0 da cui k≤ 0 o K≥ 8

Data l’equazione parametrica x²-(k-2)x+k+1=0, determiniamo i valori di k in modo che, essendo le soluzioni reali: A) Una radice sia l’opposto dell’altra. B) Una radice sia uguale a 2. C) Una radice sia l’inverso dell’altra. D) Il prodotto delle radici sia uguale a

A)UNA RADICE SIA L’OPPOSTO DELL’ALTRA SE: X 1= -X 2 cioè X 1 - X 2=0 ma X 1+ X 2= b/a, basta quindi imporre che sia k-2= 0 k=2 Per questo valore di k, tuttavia, le soluzioni non sono reali e dobbiamo concludere che il problema non ha soluzioni.

B) UNA RADICE SIA UGUALE A 2 Basta sostituire 2 al posto di X e risolvere l’equazione in k così ottenuta: 4 -2(k-2)+k+1=0 k=9 Questa volta il valore trovato di k appartiene all’insieme definito dalla condizione di realtà delle radici (9>8) èd è quindi la soluzione del

C) UNA RADICE SIA L’INVERSO DELL’ALTRA SE: X 1= 1/X 2 cioè X 1*X 2= 1 ma X 1*X 2= c/a, basta quindi imporre che sia k+1=1 k=0 per questo valore di K le soluzioni sono reali e sono anche coincidenti; ne

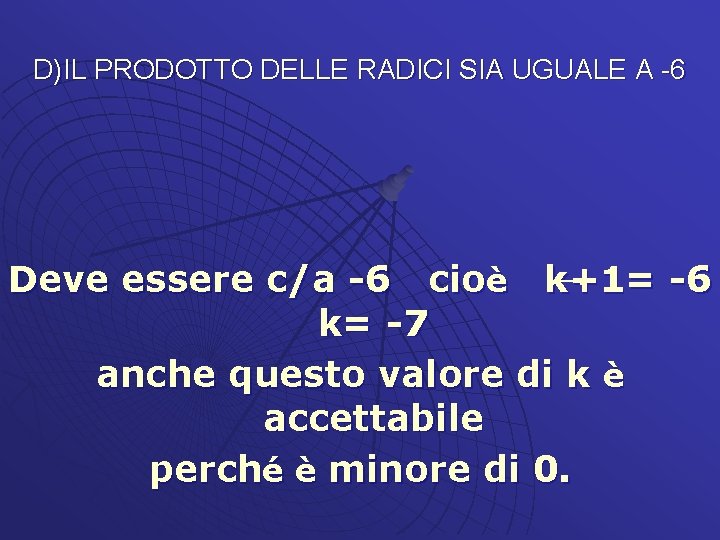
D)IL PRODOTTO DELLE RADICI SIA UGUALE A -6 Deve essere c/a -6 cioè k+1= -6 k= -7 anche questo valore di k è accettabile perché è minore di 0.