snick snack CPSC 121 Models of Computation 20089

snick snack CPSC 121: Models of Computation 2008/9 Winter Term 2 Functions Steve Wolfman, based on notes by Patrice Belleville and others

Lecture Prerequisites Read Section 7. 1. Solve problems like Exercise Set 7. 1, #1 -4, 13 -14, 23 -24.

Learning Goals: Pre-Class By the start of class, you should be able to: – Define the terms domain, co-domain, range, image, and pre-image – Use appropriate function syntax to relate these terms (e. g. , f : A B indicates that f is a function mapping domain A to codomain B). – Determine whether f : A B is a function given a definition for f as an equation or arrow diagram.

Learning Goals: In-Class By the end of this unit, you should be able to: – Define the terms injective (one-to-one), surjective (onto), bijective (one-to-one correspondence), and inverse. – Determine whether a given function is injective, surjective, and/or bijective. – Apply your proof skills to proofs about the properties (e. g. , injectiveness, surjectiveness, bijectiveness, and function-ness) of functions and their inverses.

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition Dropped from learning goals and exam.

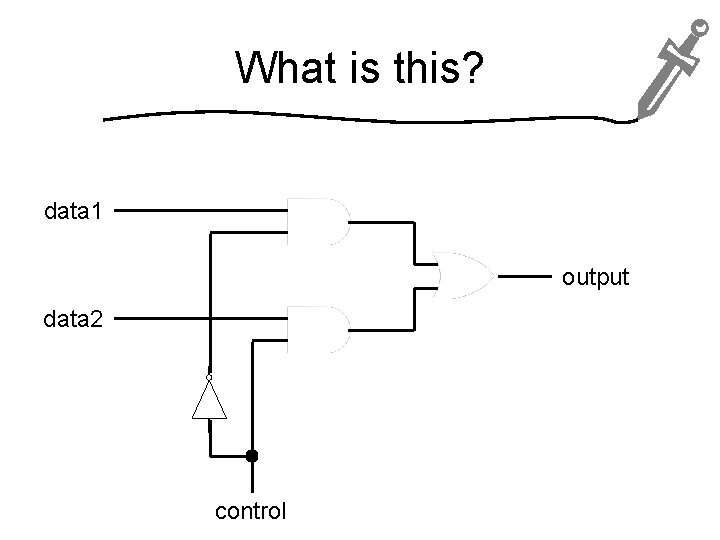
What is this? data 1 output data 2 control

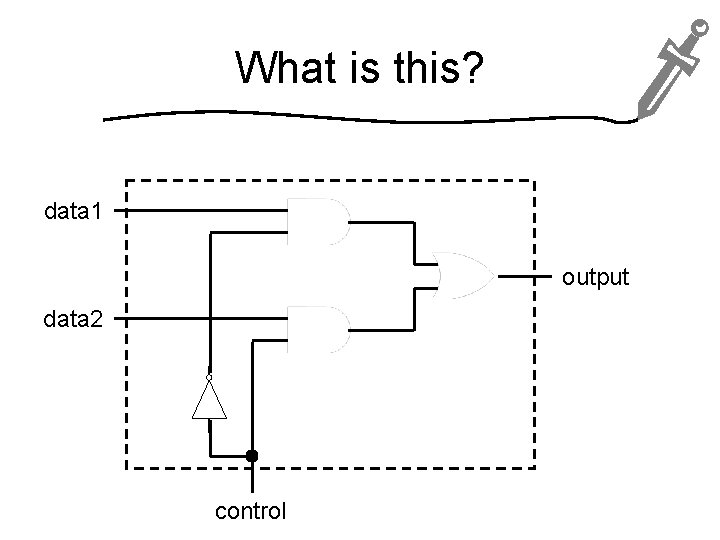
What is this? data 1 output data 2 control

What is this? data 1 output data 2 control

What is this? In the lab, you implemented a multiplexer and then used it as a piece in larger circuits. You abstracted from the concrete implementation to a description of its function: f(control, data 1, data 2) = output = (~control data 1) (control data 2) = data 1 if control is 0, data 1 but data 2 otherwise output data 2 control

Functions, Abstraction, and CPSC 121 Computer scientists use many abstraction levels, with reasoning and often execution tools at each level. In 121, we learn tools for some key abstraction levels: wiring physical gates, computer-based hardware design techniques, propositional logic, predicate logic, sets, … Functions are a new level that let us talk about how computations work and fit together. Bonus: functions alone are enough for all of computation, using the “λ calculus”.

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition

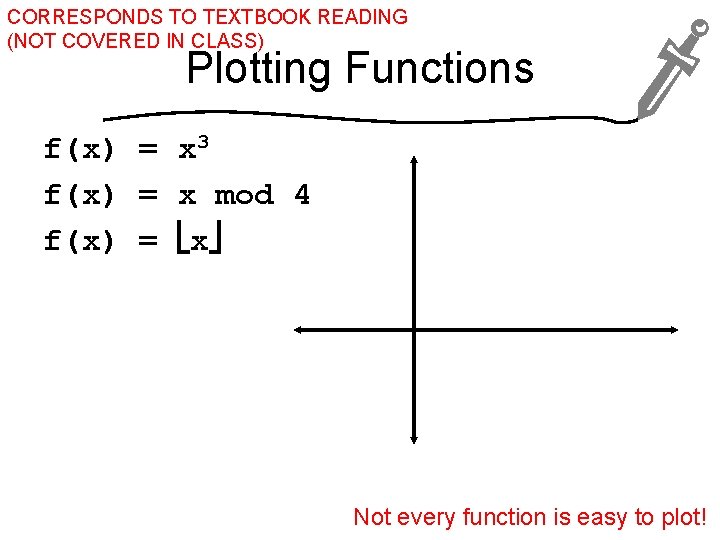
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) What is a Function? Mostly, a function is what you learned it was all through K-12 mathematics, with strange vocabulary to make it more interesting… A function f: A B maps values from its domain A to its co-domain B. Domain Co-domain f(x) = x 3 f(x) = x mod 4 f(x) = x Look, sets!

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Plotting Functions f(x) = x 3 f(x) = x mod 4 f(x) = x Not every function is easy to plot!

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) What is a Function? Not every function has to do with numbers… A function f: A B maps values from its domain A to its co-domain B. Domain f(x) = ~x f(x, y) = x y f(x) = x’s phone # Co-domain

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) What is a Function? A function f: A B maps values from its domain A to its co-domain B. f(control, data 1, data 2) = (~control data 1) (control data 2) Domain? Co-domain?

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) What is a Function? A function f: A B maps values from its domain A to its co-domain B. Alan Steve 111 Paul 121 Patrice 211 Karon George Domain? Co-domain? Other examples?

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) What is a Function? A function f: A B maps values from its domain A to its co-domain B. f can’t map one element of its domain to more than one element of its co-domain: x A, y 1, y 2 B, [(f(x) = y 1) (f(x) = y 2)] (y 1 = y 2). f Why insist on this? A B

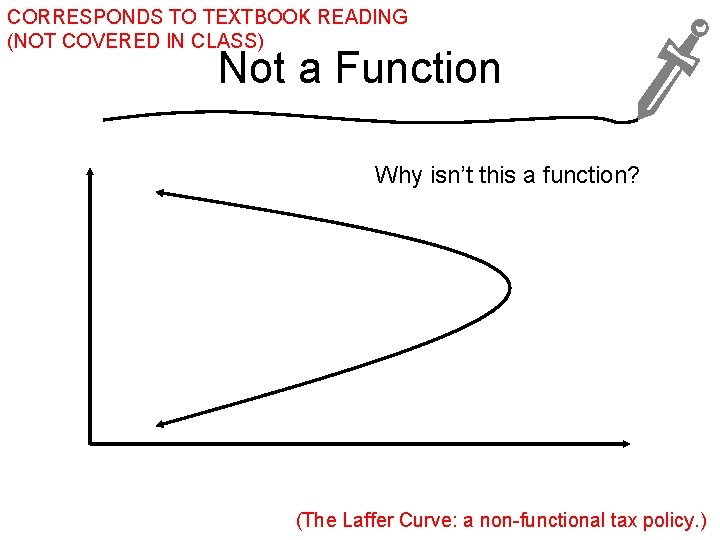
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Not a Function Why isn’t this a function? (The Laffer Curve: a non-functional tax policy. )

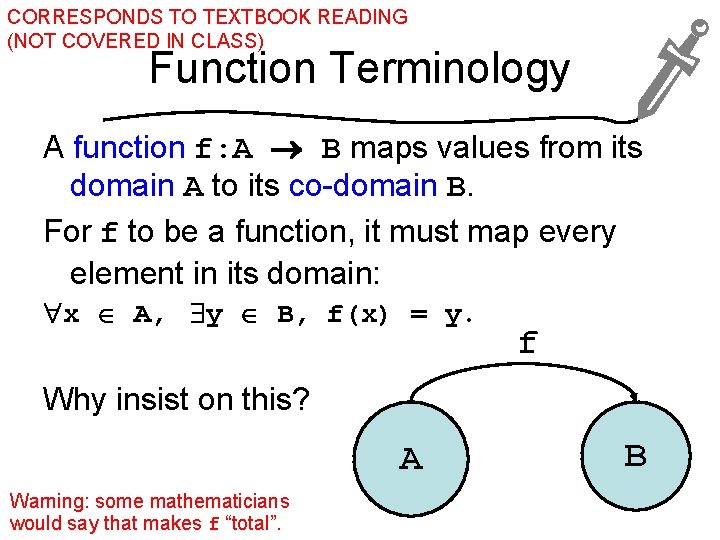
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Function Terminology A function f: A B maps values from its domain A to its co-domain B. For f to be a function, it must map every element in its domain: x A, y B, f(x) = y. f Why insist on this? A Warning: some mathematicians would say that makes f “total”. B

CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Not a Function Anne Alan Steve 111 Paul 121 Patrice 211 Karon George Foiled by sabbatical.

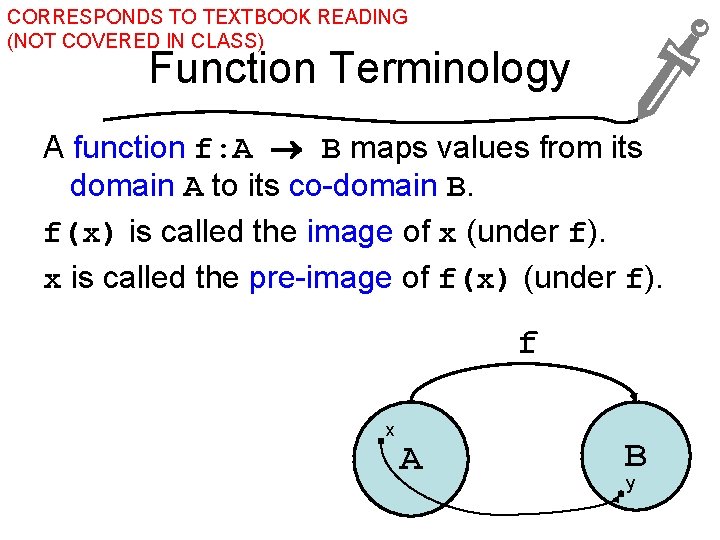
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Function Terminology A function f: A B maps values from its domain A to its co-domain B. f(x) is called the image of x (under f). x is called the pre-image of f(x) (under f). f x A B y

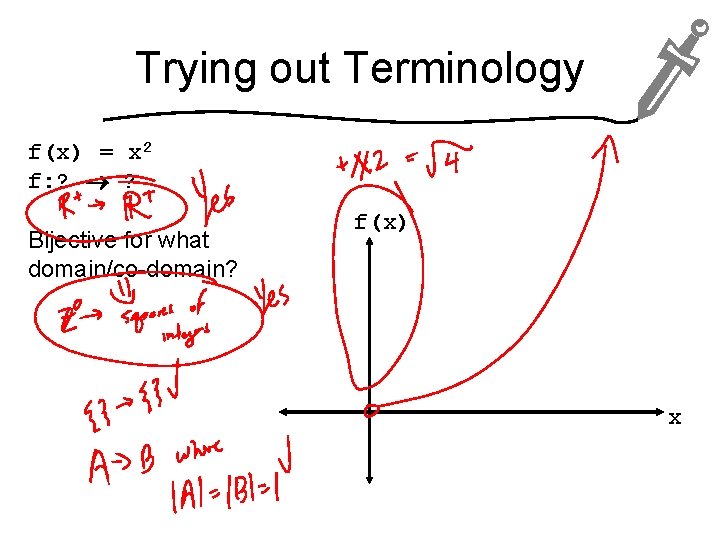
CORRESPONDS TO TEXTBOOK READING (NOT COVERED IN CLASS) Trying out Terminology f(x) = x 2 What is the image of 16? What is the range of f? f(x) x

Functions We’ve Used • Any combinational logic circuit • The “inverse” and “zip” operations over algorithms from the midterm • The operation that gives you a student’s grade given the student: G(s) = s’s grade • Arrays, as long as they’re immutable (unchangeable): A(i) = the ith value in array A. Sequential circuits and mutable arrays aren’t functions. Why not? (Actually we can model them as functions by making time explicit)

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition

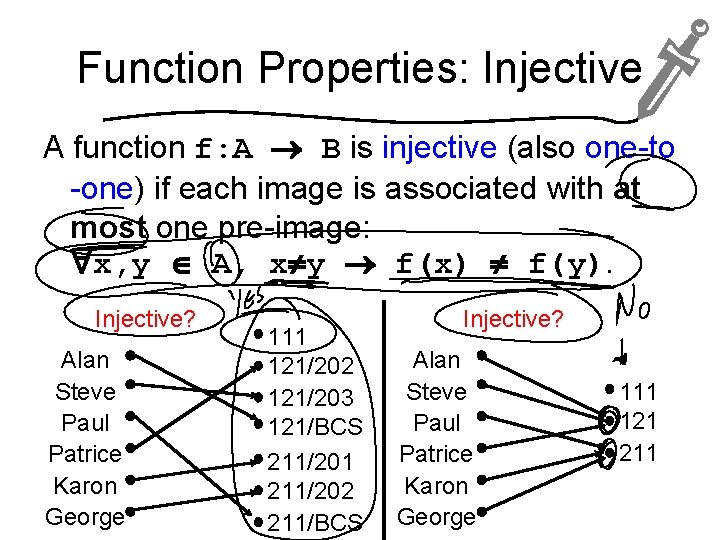
Function Properties: Injective A function f: A B is injective (also one-to -one) if each image is associated with at most one pre-image: x, y A, x y f(x) f(y). Injective? Alan Steve Paul Patrice Karon George 111 121/202 121/203 121/BCS 211/201 211/202 211/BCS Injective? Alan Steve Paul Patrice Karon George 111 121 211

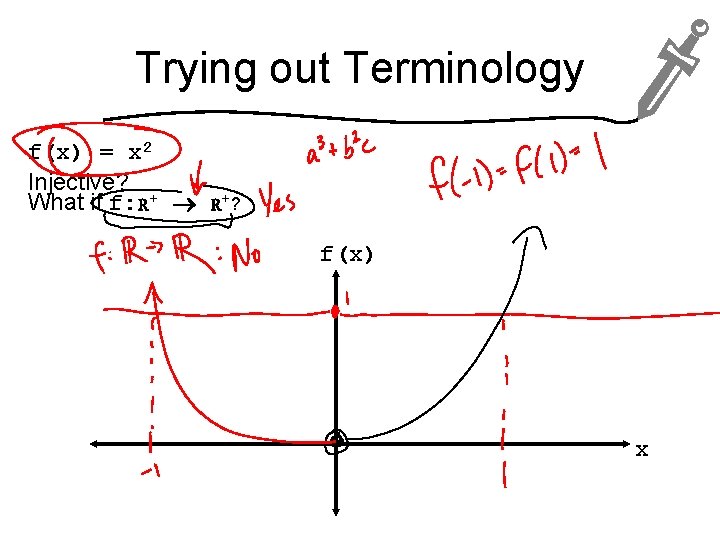
Trying out Terminology f(x) = x 2 Injective? What if f: R+ R+? f(x) x

Trying out Terminology f: {s|s is a 121 student} {A+, A, …, D, F} f(s) = s’s mark in 121 Is f injective? What if we didn’t know what f represented, only its “type” and the fact that there are lots of 121 students: f: {s|s is a 121 student} {A+, A, …, D, F}

Nifty Injective Function: Error-Correcting Codes Error-correcting codes must be injective. Why?

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition

Function Properties: Surjective f: A B is surjective (also onto) if every element of the co-domain has a pre-image: y B, x A, y = f(x). Surjective? Alan Steve Paul Patrice Karon George 111 121/202 121/203 121/BCS 211/201 211/202 211/BCS Surjective? Alan Steve Paul Patrice Karon George 121 211 Can we define “surjective” in terms of “range” and “co-domain”?

Trying out Terminology f(x) = x 2 f: R R 0? Surjective? What if f: R R? What if f: Z Z 0? How about f(x) = x ? For what types is it surjective? f(x) x

Trying out Terminology f: {s|s is a 121 student} {A+, A, …, D, F} f(s) = s’s mark in 121 Is f surjective? Could we ever know that f was surjective just by knowing f’s domain and co-domain?

Nifty Surjective Function: “Lossy” Compression WARNING: Lossy compression functions are not always surjective… But it’s valuable if they are. Why?

Surjective Functions So Far Under what circumstances is a combinational circuit with one ouput surjective? Under what circumstances is it not surjective? So, are our circuits usually surjective or not?

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition

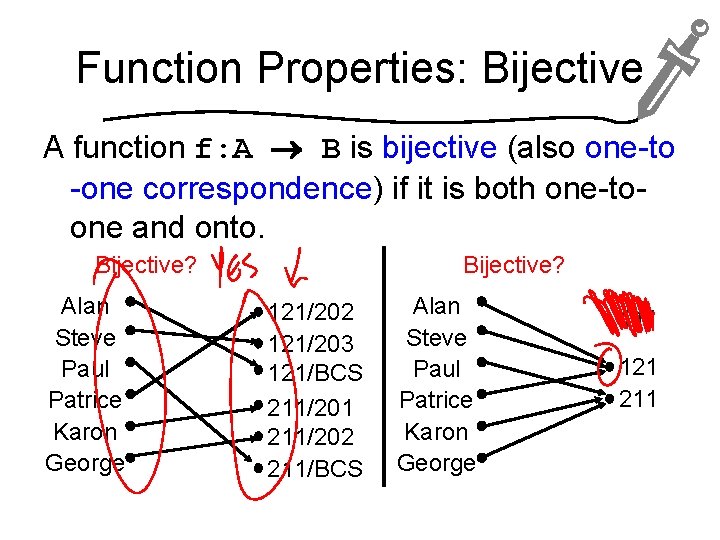
Function Properties: Bijective A function f: A B is bijective (also one-to -one correspondence) if it is both one-toone and onto. Every element in the domain has exactly one unique image. Every element in the co-domain has exactly one unique preimage.

Function Properties: Bijective A function f: A B is bijective (also one-to -one correspondence) if it is both one-toone and onto. Bijective? Alan Steve Paul Patrice Karon George Bijective? 121/202 121/203 121/BCS 211/201 211/202 211/BCS Alan Steve Paul Patrice Karon George 111 121 211

Trying out Terminology f(x) = x 2 f: ? ? Bijective for what domain/co-domain? f(x) x

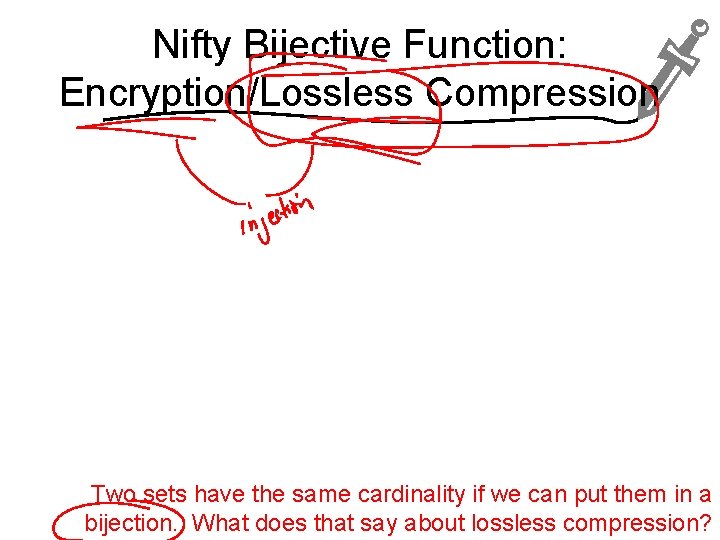
Nifty Bijective Function: Encryption/Lossless Compression Two sets have the same cardinality if we can put them in a bijection. What does that say about lossless compression?

Outline • Functions as “Computation Abstractions” • Definition of Functions and Function Terminology • Function Properties – Injective – Surjective – Bijective • Function Operations – Inverse – Composition

Function Operations: Inverse The inverse of a function f: A B is f-1: B A. f(x) = y f-1(y) = x. How can we tell whether f-1 is a function? (Hint: what would make f-1 not a function? ) Can we prove it?

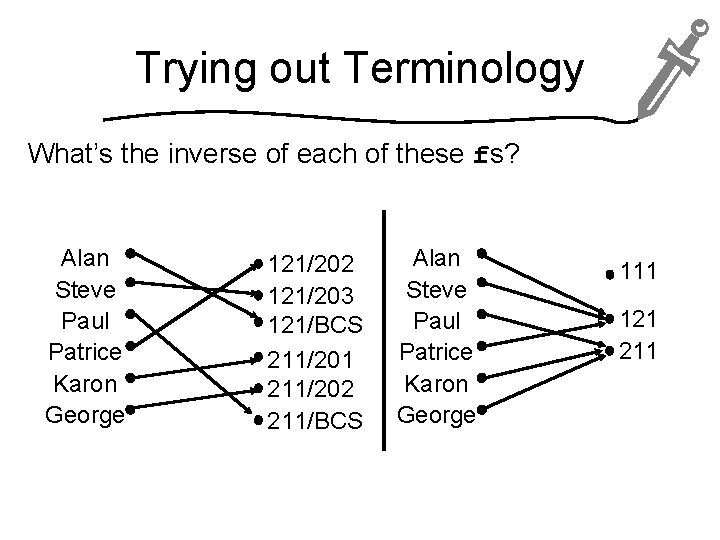
Trying out Terminology What’s the inverse of each of these fs? Alan Steve Paul Patrice Karon George 121/202 121/203 121/BCS 211/201 211/202 211/BCS Alan Steve Paul Patrice Karon George 111 121 211

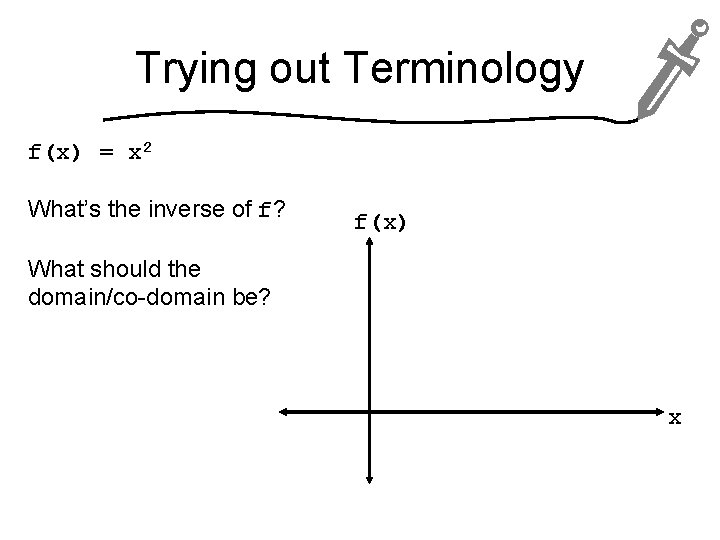
Trying out Terminology f(x) = x 2 What’s the inverse of f? f(x) What should the domain/co-domain be? x

Proving a function injective Recall: A function f : A B is injective exactly when: x, y A, x y f(x) f(y). A typical approach is to prove the contrapositive by antecedent assumption: assume f(x) = f(y) and show that x = y.

Problem: x 3 + 5 is injective Theorem: f(x) = x 3 + 5 is injective, where f : Z Z.

Proving a function surjective Recall: A function f : A B is surjective exactly when: y B, x A, y = f(x). That existential gives us a lot of freedom to pick a witness! A typical approach is to “solve for” the necessary x given a y.

Problem: w + 2 z is surjective Theorem: f(w, z) = w + 2 z is surjective, where f : (Z Z) Z.

Proving a function bijective Prove that it’s injective. Prove that it’s surjective. Done.

Proving a function has an inverse Prove that it’s bijective. Done.

An Inverse Proof Theorem: If f: A B is bijective, then f-1 : B A is a function. Recall that f-1(f(x)) = x.

Aside: Functions are Just Sets We can define functions in terms of sets and tuples (and we can define tuples in terms of sets!). The function f: A B is the set {(x, f(x)) | x A}. f is a subset of A B!

Learning Goals: In-Class By the end of this unit, you should be able to: – Define the terms injective (one-to-one), surjective (onto), bijective (one-to-one correspondence), and inverse. – Determine whether a given function is injective, surjective, and/or bijective. – Apply your proof skills to proofs about the properties (e. g. , injectiveness, surjectiveness, bijectiveness, and function-ness) of functions and their inverses.