snick snack CPSC 121 Models of Computation 20089

snick snack CPSC 121: Models of Computation 2008/9 Winter Term 2 Propositional Logic: A First Model of Computation Steve Wolfman, based on notes by Patrice Belleville and others

Introductions, again Steven Wolfman (call me Steve!) wolf@cs. ubc. ca ICICS 239; office hours: Mon, Tue, Wed 10 -12 and Thu 2 -4 but I have an open door policy: If my door is open, come in and talk! Also, I will usually be available after class. And, you can make appointments with me.

Quiz 1 Notes (1 of 2) Biggest issue: how do I start solving the problem? • What is it asking (both informally and formally)? • What is the answer, ignoring propositional logic? • How do we model the problem in propositional logic? • Where do I go from there?

Quiz 1 Notes (2 of 2) Switch problem: • What happens when all are on? • Do we need “state”? • Problems with XOR PC problem • What is the intended output (in normal numbers)? • How many outputs are there (in propositional logic)? • How do we get formulas for those? • How do we simplify?

Lecture Prerequisites Read Sections 1. 1 and 1. 4 Solve problems like Exercise Set 1. 1, #1 -18 and Exercise Set 1. 4, #1 -17. You should have completed the open-book, untimed quiz on Web. CT that was due before this class.

Learning Goals: Pre-Class By the start of class, you should be able to: – Translate back and forth between simple natural language statements and propositional logic. – Evaluate the truth of propositional logic statements using truth tables. – Translate back and forth between propositional logic statements and circuits that assess the truth of those statements.

Learning Goals: In-Class By the end of this unit, you should be able to: – Build combinational computational systems using propositional logic expressions and equivalent digital logic circuits that solve real problems, e. g. , our 7 - or 4 -segment LED displays. – Evaluate propositional logic as a “model of computation” for combinational circuits, including at least one explicit shortfall (e. g. , referencing gate delays, fan-out, transistor count, wire length, instabilities, shared sub-circuits, etc. ). The second goal is really a multi-unit goal that we will start working with this unit.

Logic as Tool for Reasoning about Truth Where should we start?

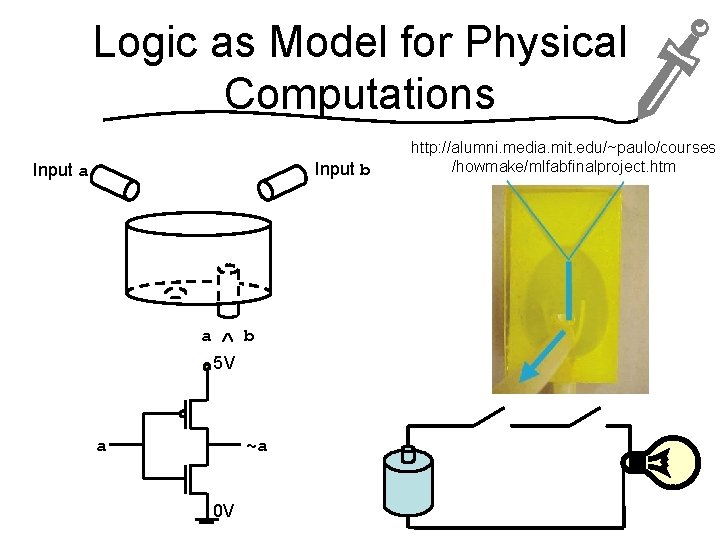
Logic as Model for Physical Computations Input b Input a a b 5 V a ~a 0 V http: //alumni. media. mit. edu/~paulo/courses /howmake/mlfabfinalproject. htm

Problem: Two-Way Switch Problem: Build a circuit to control a light so that the light changes state any time either of the two switches that control it is flipped.

Digital Logic Challenges If you finish early, discuss the problem with your neighbours, try a related problem, or don’t just build a circuit, build one that… • • Has minimum or uniform “gate delay” Uses the fewest transistors Uses the fewest gates across the whole circuit Uses minimum area/wiring length on the circuit

Concept Q: 2 -Way Switch In general, not just in your solution, is the light on or off when both switches are up? (Pick the best answer. ) a. On, in every correct solution. b. Off, in every correct solution. c. It depends, though any single correct solution should always do the same thing. d. It depends, and a single correct solution might do different things at different times. e. Neither on nor off.

Problem: Three-Way Switch Problem: Build a circuit to control a light so that the light changes state any time any of the three switches that control it is flipped.

Concept Q: Three-Way Switch In your circuit, which of these tells you with certainty whether the light is on or off? (Pick the best answer. ) a. Whether an odd number of switches is on. b. Whether the majority (two or more) of switches are on. c. Whether all the switches are on. d. Whether a switch has been flipped recently. e. None of these.

Problem: 7 -Segment LED Display Problem: build a circuit that displays the numbers 0 through 9 represented by four Boolean values p, q, r, and s. (The whole problem requires a lot of grunt work. Please pick one segment, and solve the problem for that segment. )

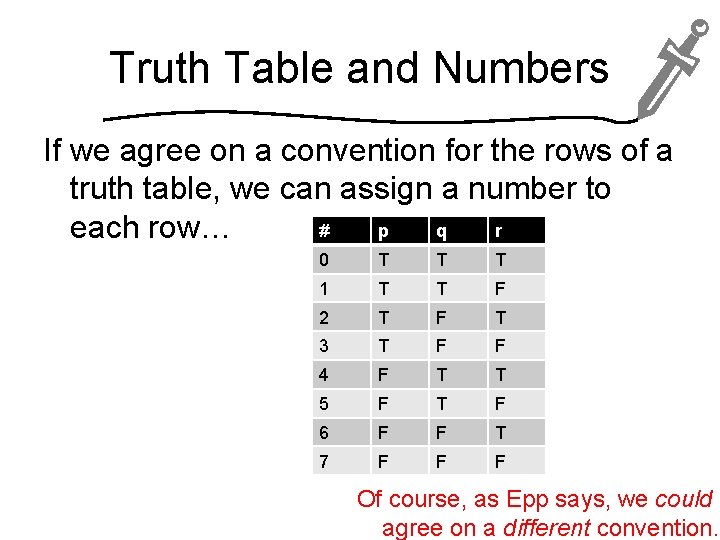
Truth Table and Numbers If we agree on a convention for the rows of a truth table, we can assign a number to # p q r each row… 0 T T T 1 T T F 2 T F T 3 T F F 4 F T T 5 F T F 6 F F T 7 F F F Of course, as Epp says, we could agree on a different convention.

Representing Positive Integers This is the convention we (and computers) use for the positive integers 0 -9, which requires 4 variables: # a b c d 0 F F 8 T F F F 1 F F F T 9 T F F T 2 F F T F 3 F F T T 4 F T F F 5 F T 6 F T T F 7 F T T T Just the opposite of our previous version.

Concept Q: 7 -Segment LED Imagine we were working on an LED in a display for some other kind of number (like Roman numerals). Which of these would definitely make our problem easier? a. More entries in the LED’s column of the truth table that are true (turn some Fs into Ts). b. Fewer entries in the LED’s column of the truth table that are true (turn some Ts into Fs). c. More legal inputs (e. g. , 0 -9 and “A” for 10). d. Fewer legal inputs (e. g. , only 0 -8). e. None of these would definitely make the problem easier.

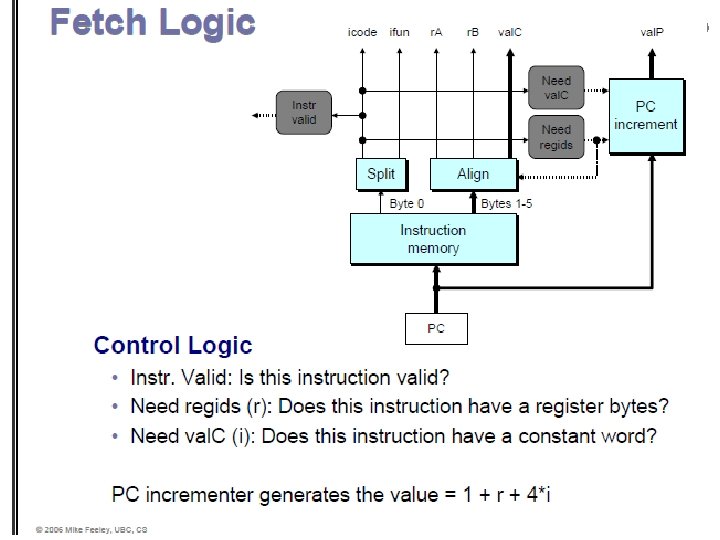
Problem: Updating the “PC” Problem: Create logic that calculates the amount to increase the PC by, given the values Need. Val. C and Need. Reg. IDs.

Problem: Updating the “PC”

Concept Q: Fetch Logic What’s the minimum number of Boolean outputs necessary for this circuit? a. 1 b. 2 c. 3 d. 4 e. Cannot be determined from the information given.

Learning Goals: In-Class By the end of this unit, you should be able to: – Build combinational computational systems using propositional logic expressions and equivalent digital logic circuits that solve real problems, e. g. , our 7 - or 4 -segment LED displays. – Evaluate propositional logic as a “model of computation” for combinational circuits, including at least one explicit shortfall (e. g. , referencing gate delays, fan-out, transistor count, wire length, instabilities, shared sub-circuits, etc. ). Bonus goal that foreshadows “induction”: Give two examples of recursive definitions.

Next Lecture Learning Goals: Pre-Class By the start of class, you should be able to: – Translate back and forth between simple natural language statements and proposition logic, now with conditionals and biconditionals. – Evaluate the truth of propositional logical statements that include conditionals and biconditionals using truth tables. – Given a propositional logic statement and an equivalence rule, apply the rule to create an equivalent statement. Example: Note: Result: given (u s) s, apply p q ~p q. p maps to (u s) and q maps to s. ~(u s) s

Next Lecture Prerequisites Reread Sections 1. 1 and 1. 4. Read Section 1. 2. Solve problems like Exercise Set 1. 1, #1929, and 39 -46; Set 1. 2, #5 -15, 20, 22, and 38 -46; and Set 1. 4, #26 -32. Complete the open-book, untimed quiz on Web. CT that’s due before the next class.

snick snack More problems to solve. . . (on your own or if we have time)

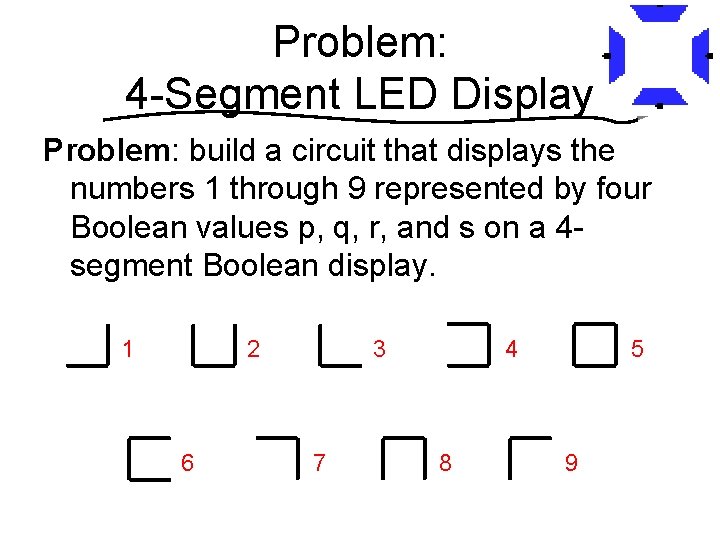
Problem: 4 -Segment LED Display Problem: build a circuit that displays the numbers 1 through 9 represented by four Boolean values p, q, r, and s on a 4 segment Boolean display. 1 2 6 3 7 4 8 5 9

Problem: One-Bit Addition Problem: build a circuit that takes three onebit numbers as input and outputs their sum as a two-bit number.

Problem: Logicians and Hats Problem: Three logicians are each wearing a black hat or a white hat, but not all white. Nobody can see their own hat. However, A can see the hats of B and C, and B can see the hats of A and C. C is blind. You go and ask them one by one in the order A, B, C, whether they know the color of their own hat. A answers “No”. B answers “No”. Then C answers “Yes”. Explain how this is possible.

Problem: Criminals and Hats Problem: A warden plans to line up 100 prisoners in order tomorrow. The warden will place a white or black hat on each prisoner’s head so that no prisoner can see the hat on his or her own head, but they can see the hats of the prisoners in front of them. From the back of the line, the warden will ask each prisoner “Is your hat black? ” If the prisoner answers correctly, he or she is set free. Incorrect answers lead to immediate and noisy beheading. If they answer anything other than “yes” or “no”, all prisoners are beheaded. They get one hour as a group to plan their strategy. How many prisoners can be saved? The three-way light switch might give you a hint.