SemiLagrangian Approximation in the Time Dependent NavierStokes Equations















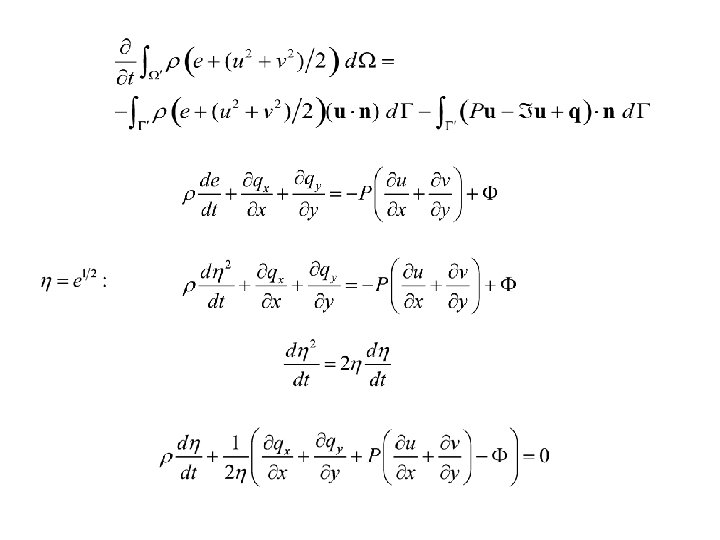







- Slides: 34

Semi-Lagrangian Approximation in the Time. Dependent Navier-Stokes Equations Vladimir V. Shaydurov Institute of Computational Modeling of Siberian Branch of Russian Academy of Sciences, Krasnoyarsk Beihang University, Beijing shaidurov 04@mail. ru in cooperation with G. Shchepanovskaya and M. Yakubovich

Contents • Convection-diffusion equations: Modified method of characteristics. • Conservation law of mass: Approximation in norm. • Finite element method: Approximation in norm.

• Pironneau O. (1982): Method of characteristics The main feature of several semi-Lagrangian approaches consists in approximation of advection members as one “slant” (substantial or Lagrangian) derivative in the direction of vector

Pointwise approach in convection-diffusion equation The equation with this right-hand side is self-adjoint.

Approximation of slant derivative Apply finite element method at the time level and use appropriate quadrature formulas for the lumping effect Two ways for approximation of slant derivative 1. Approximation along vector 2. Approximation along characteristics (trajectory)

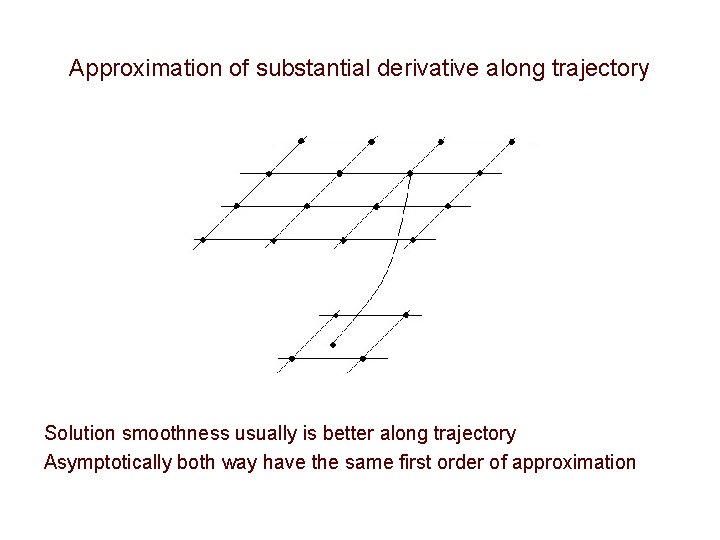
Approximation of substantial derivative along trajectory Solution smoothness usually is better along trajectory Asymptotically both way have the same first order of approximation

Finite element formulation at time level Intermediate finite element formulation Final formulation

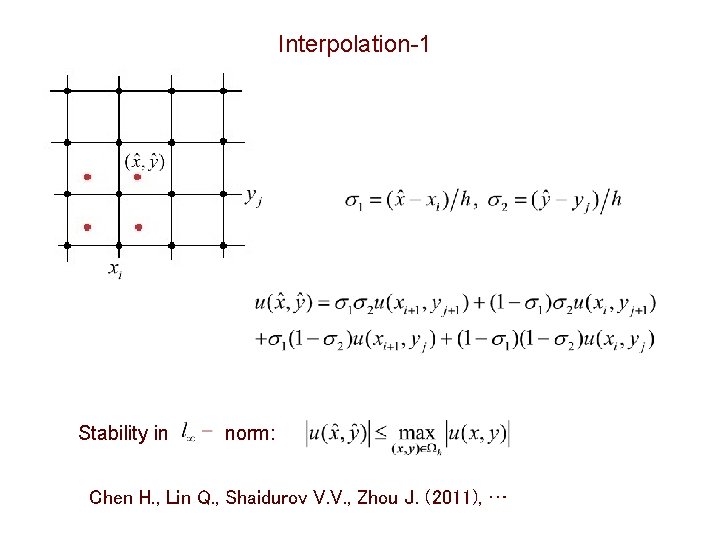
Interpolation-1 Stability in norm: Chen H. , Lin Q. , Shaidurov V. V. , Zhou J. (2011), …

Interpolation-1 Stability in norm and conservation law: impact of four neighboring points into the weight of

Interpolation-2

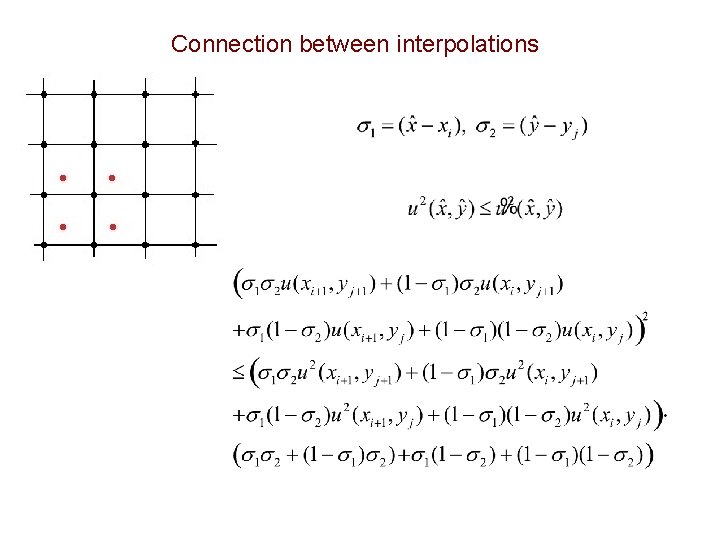
Connection between interpolations

Improving by higher order differences

Solving two problems with the first and second order of accuracy

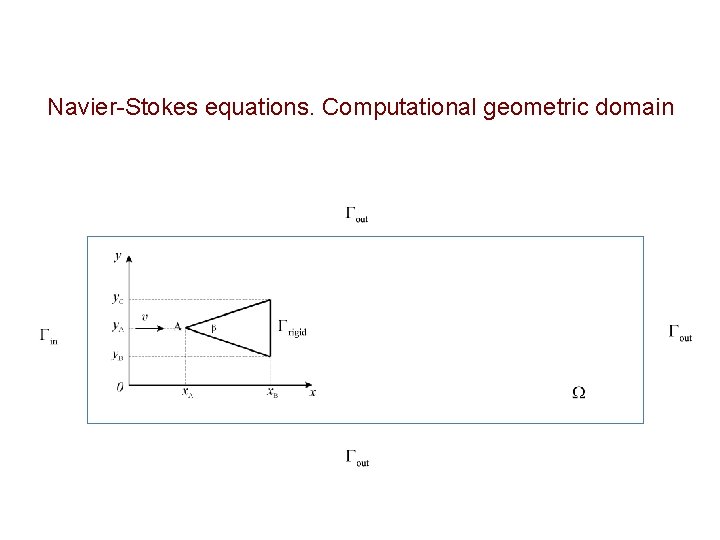
Navier-Stokes equations. Computational geometric domain

Navier-Stokes equations In the cylinder we write 4 equations in unknowns

Notation

Notation

Notation

Initial and boundary conditions
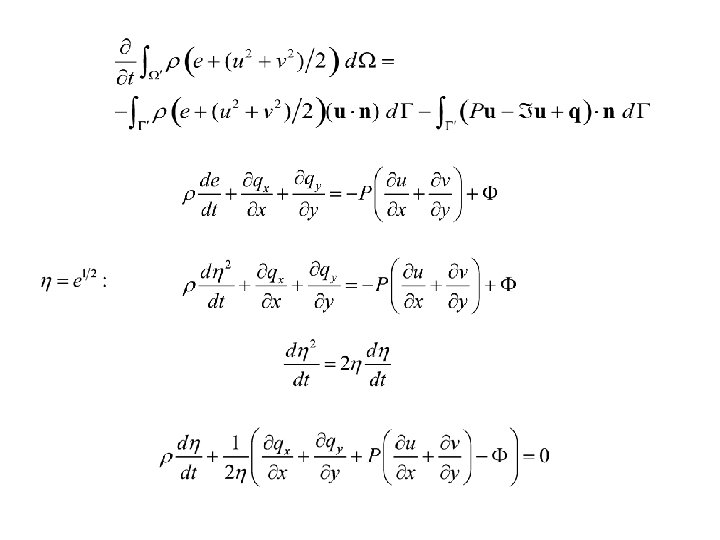

Boundary conditions at outlet supersonic and rigid boundary

Boundary conditions at subsonic part of computational boundary a wake

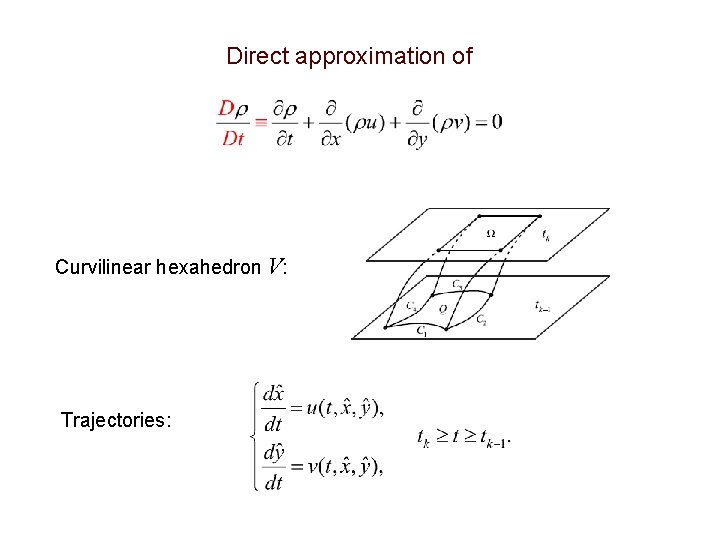
Direct approximation of Curvilinear hexahedron V: Trajectories:

Due to Gauss-Ostrogradskii Theorem: Approximation of curvilinear quadrangle Q:

Gauss-Ostrogradskii Theorem in the case of boundary conditions:

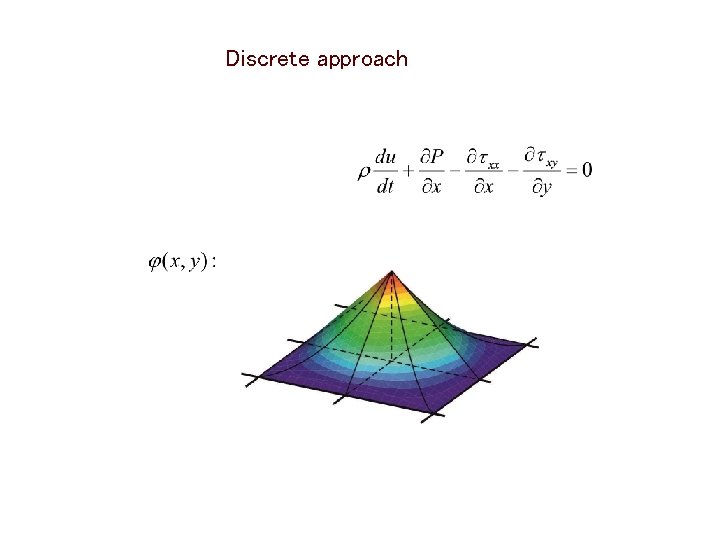
Discrete approach

Matrix of finite element formulation at time layer

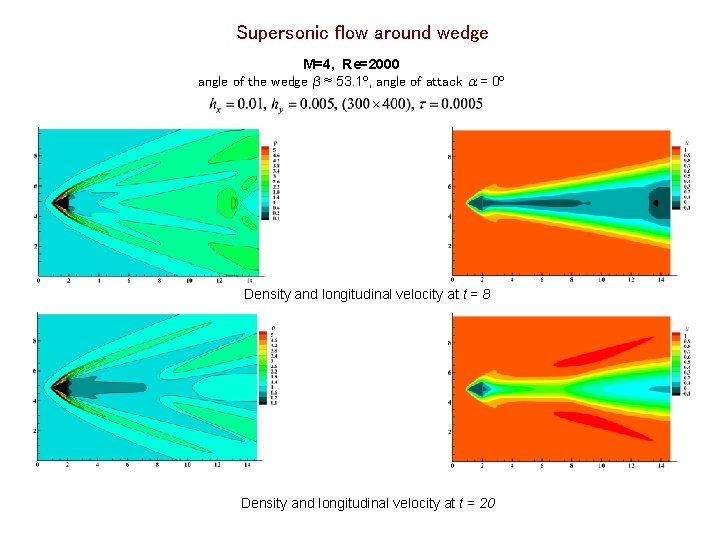
Supersonic flow around wedge M=4, Re=2000 angle of the wedge β ≈ 53. 1º, angle of attack = 0º Density and longitudinal velocity at t = 8 Density and longitudinal velocity at t = 20

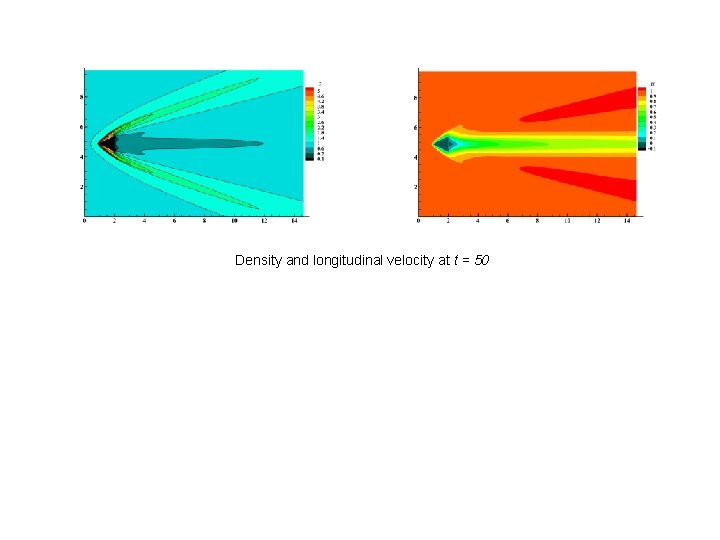
Density and longitudinal velocity at t = 50

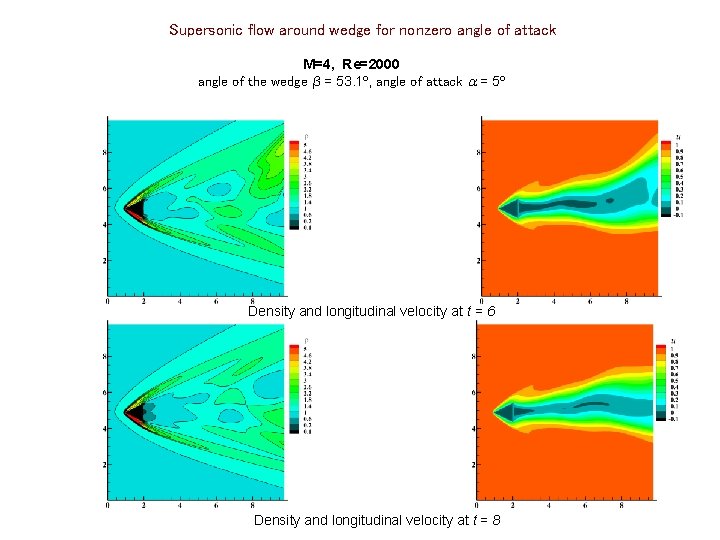
Supersonic flow around wedge for nonzero angle of attack M=4, Re=2000 angle of the wedge β = 53. 1º, angle of attack = 5º Density and longitudinal velocity at t = 6 Density and longitudinal velocity at t = 8

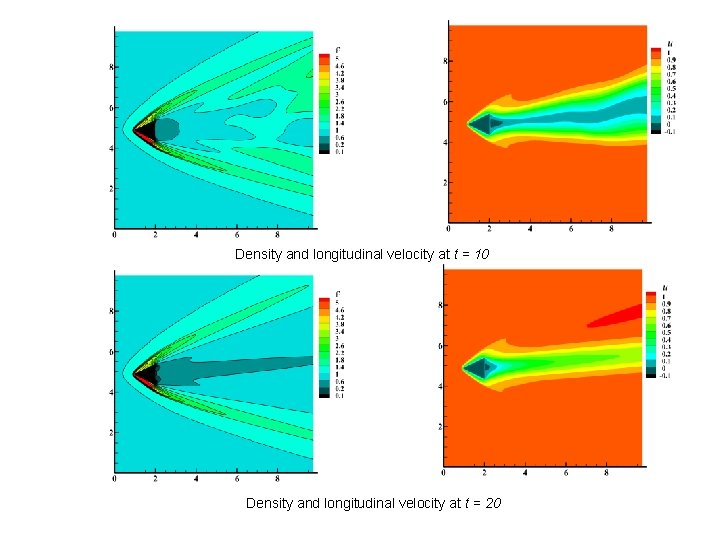
Density and longitudinal velocity at t = 10 Density and longitudinal velocity at t = 20

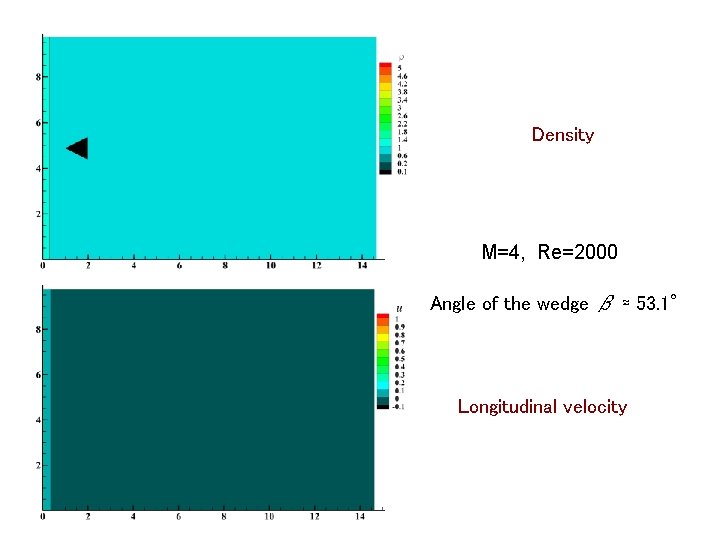
Density M=4, Re=2000 Angle of the wedge β ≈ 53. 1° Longitudinal velocity

Conclusion • Conservation of full energy (kinetic + inner) • Approximation of advection derivatives in the frame of finite element method without artificial tricks • The absence of Courant-Friedrichs-Lewy restriction on the relation between temporal and spatial meshsizes • Discretization matrices at each time level have better properties • The better smooth properties and the better approximation along trajectories

• Thanks for your attention!
 Fully polynomial time approximation scheme
Fully polynomial time approximation scheme What is elapsed time
What is elapsed time Is sinx acceptable wave function
Is sinx acceptable wave function What is the hamiltonian operator
What is the hamiltonian operator Schrodinger time dependent equation
Schrodinger time dependent equation Time independent schrodinger equation
Time independent schrodinger equation Time dependent schrodinger wave equation
Time dependent schrodinger wave equation Schrodinger time dependent equation
Schrodinger time dependent equation Future time clauses structure
Future time clauses structure Scleronomous meaning
Scleronomous meaning Variational shape approximation
Variational shape approximation Simpson's 3/8 rule
Simpson's 3/8 rule Trapazoidal sum
Trapazoidal sum First order taylor approximation
First order taylor approximation First born approximation
First born approximation Transversality condition
Transversality condition Normal approximation to binomial calculator
Normal approximation to binomial calculator Geoid shape
Geoid shape Steady state approximation in chemical kinetics
Steady state approximation in chemical kinetics Eukers method
Eukers method Miller practice
Miller practice Cultural approximation
Cultural approximation Continuous least squares approximation
Continuous least squares approximation First approximation of diode
First approximation of diode Vogel's approximation method
Vogel's approximation method Normal approximation calculator
Normal approximation calculator Linear approximation
Linear approximation Remnote updates
Remnote updates The gas phase decomposition of acetic acid at 1189 k
The gas phase decomposition of acetic acid at 1189 k First born approximation
First born approximation Under what conditions does an alternating series converge?
Under what conditions does an alternating series converge? Vam stands for vogels approximation ___________________.
Vam stands for vogels approximation ___________________. Approximation algorithms vazirani
Approximation algorithms vazirani Genfit mathcad
Genfit mathcad Catalysis by approximation
Catalysis by approximation